震级是地震三要素之一,准确测定震级对于地震速报与应急等工作至关重要(董海龙等,2015)。地震波在地壳中传播时遇到的断裂和不同的特性岩石介质会对震级的精确测定造成影响(李惠智,2009;田文德等,2012;吴微微等,2014)。在日常观测中发现,灌云地震台(灌云台)测定的远震震级与中国地震台网中心公布的震级存在一定的偏差,例如,2019年1月5日18时47分(世界时)发生在印度尼西亚松巴岛地区的地震,灌云地震台测定震级为5.5,而中国地震台网中心公布的震级为6.0,二者相差0.5,并且对于不同的震级、震中距和方位角,偏差大小也有所不同。通过查阅相关文献,发现前人将单台震级与中国地震台网中心公布的震级做差,然后将多次结果计算平均值,以此结果作为震级偏差校正值(中国地震局监测预报司,2003)。因此,有必要进行震级偏差计算,对偏差原因进行分析,给出校正值。这对于提高观测精度、提升台站监测能力具有重要意义。
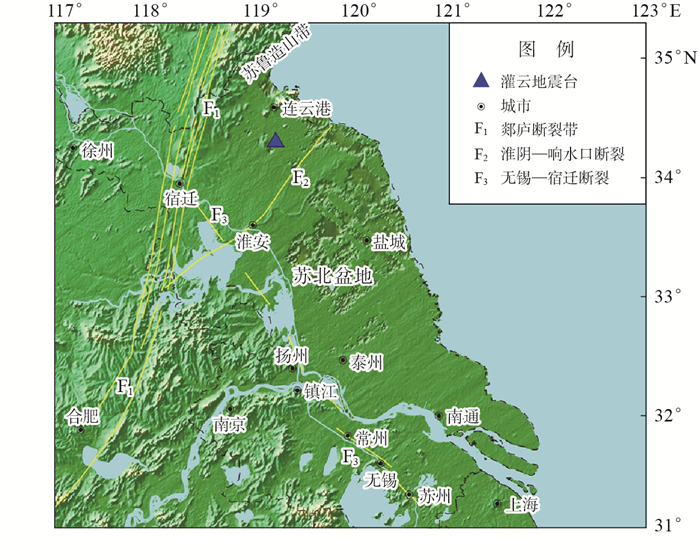
1 台站简介灌云地震台(下文简称灌云台)建于1973年,位于江苏省北部的连云港市灌云县,处于苏北盆地北部,其北部为苏鲁造山带、西侧为我国东部著名的郯庐断裂带,南侧为淮安—响水断裂带(余腾等,2020;何奕成等,2021)(图 1)。台站基岩出露,台基岩性为花岗片麻岩,映震能力较强,周边无大型工厂等干扰设施,观测数据质量较高,具有优良的地震观测条件,为国家测震区域台,参与远震资料分析。灌云台配备CMG-3ESPC宽频带数字地震计,置于出露基岩上。
|
图 1 江苏及邻区主要地质构造示意 Fig.1 Schematic diagram of the major geological structures in Jiangsu and its neighboring areas |
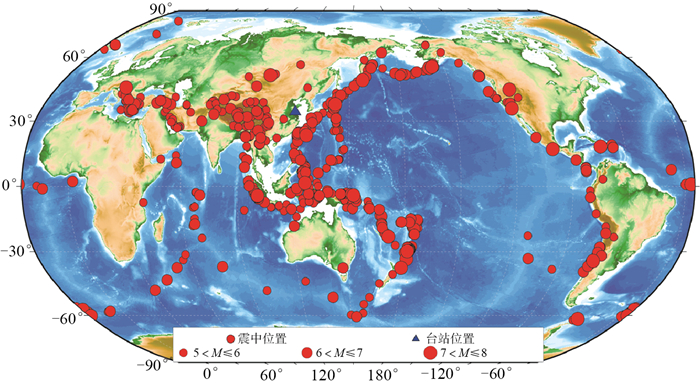
选取灌云台2019年1月—2021年12月记录的远震事件波形数据,筛选其中记录完整的698次事件进行统计分析。统计结果显示,灌云台记录的震级范围为5.0—7.8,中国地震台网中心统一正式报目录震级范围为4.7—7.9。表 1给出数据的震级分档统计结果,可以看出,相同震级范围内,灌云台与中国地震台网中心记录的地震数不同,且灌云台记录的远震事件震级集中在MS 5.0—6.9。以中国地震台网中心统一正式报目录的地震参数为准,绘制震中分布图,如图 2。
| 表 1 震级统计 Table 1 Magnitude Statistics |
|
图 2 震中分布 Fig.2 Distribution of epicenters |
我国现行的地震面波震级计算公式由郭履灿等(1981)提出
| $M_{\mathrm{S}}=\lg \left(\frac{A}{T}\right)_{\max }+\sigma(\varDelta)+C$ | (1) |
式中,A为2个水平分向面波地动位移矢量和,单位为μm;T为对应周期,单位为s;Δ为震中距,以度(°)为单位,式中取其数值计算;C为台基校正值;σ(Δ)为面波震级起算函数,当1°<Δ<130°时,σ (Δ) =1.66lg Δ + 3.5,当130°≤Δ≤180°时,σ(Δ) = 6.775 + 0.5[(2.147e-1.4465Δ + 1.325)×(Δ - 90)×10-2 + lg sin Δ + (lgΔ - 1.954)/3]。
中国地震台网中心的震级计算公式为
| $M_{\mathrm{S}(\mathrm{CENC})}=\frac{\sum M_i}{n} \quad(i=1, 2, 3, \cdots, n)$ | (2) |
式中,Mi为各台站测定的同一地震面波震级,n为记录到同一地震的台站数。在计算MS(CENC)时,先计算平均震级,然后剔除超过给定误差范围的台站震级数据重新计算平均震级,经过多次迭代,最终得到中国地震台网中心的震级数据(訾少刚等,2006)。
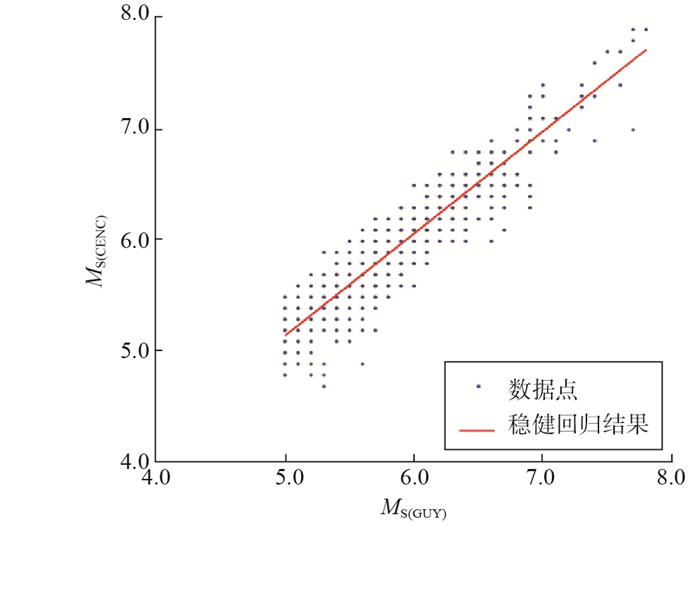
4 震级偏差分析 4.1 面波震级对应关系利用已收集整理的MS震级数据,以MS(GUY)为自变量,MS(CENC)为因变量,应用稳健回归方法(何奕成等,2016;罗伯特·安德森,2019;刘仲韬等,2021),得到MS (GUY)和MS (CENC)的关系式为
| $M_{\mathrm{S}(\mathrm{CENC})}=0.9296 M_{\mathrm{S}(\mathrm{GUY})}+0.5718 \sigma=0.173$ | (3) |
式中,σ为回归方程的均方差。根据数据绘制MS (GUY)和MS (CENC)关系图,以灌云台震级为横坐标,中国地震台网中心统一正式报目录震级为纵坐标,结果如图 3。
|
图 3 震级散点 Fig.3 Scatter diagram of magnitude |
利用做差法可以求解对于同一地震灌云台测算震级与中国地震台网中心统一正式报目录震级的偏差,公式为ΔM = MS(GUY) - MS(CENC)。利用公式
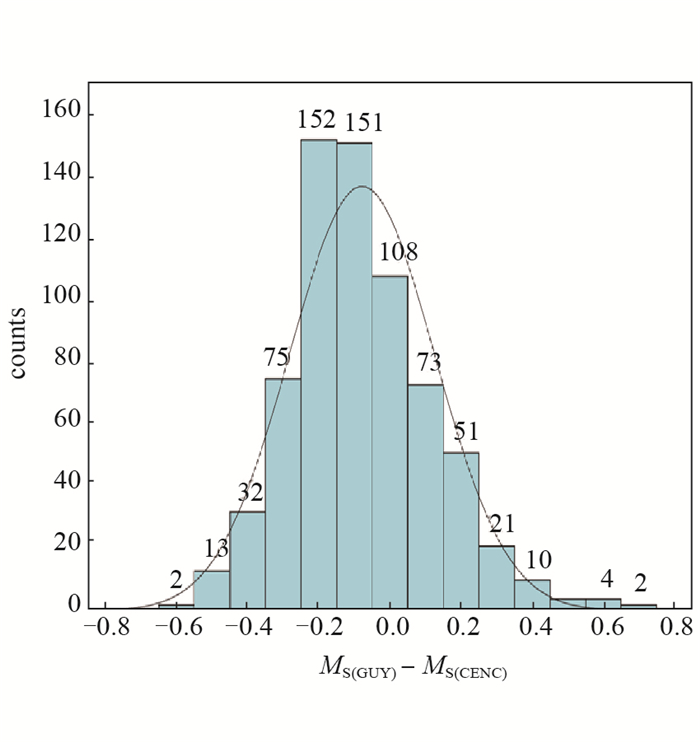
以0.1级震级偏差为间隔,统计不同震级偏差频数,绘制震级偏差频度分布图,结果见图 4,图中横坐标为震级偏差,纵坐标为对应震级偏差的地震数。由图 4可知,MS(GUY)和MS(CENC)的差值主要分布在-0.4—0.5,该范围内地震数为686个,占比98%。
|
图 4 震级偏差频度 Fig.4 Frequency of magnitude deviation |
以灌云台震级为横坐标,0.1为震级间隔,统计不同震级所对应的震级偏差平均值,得到震级与震级偏差关系,见图 5。图中横坐标为灌云台面波震级,纵坐标为震级偏差大小。由图 5可知:①在各震级档中,灌云台震级与中国地震台网中心之间震级偏差不大,最大偏差为0.2;②在MS 5.0—8.0范围内,震级偏差平均值约为-0.08,即与中国地震台网中心统一正式报目录震级相比,平均偏差仅低0.08,可以看出灌云台远震记录稳定,且偏差较小;③MS 5.0—6.5范围内,偏差折线最接近均值线,说明在该范围内的地震,灌云台的记录的震级偏差最小。
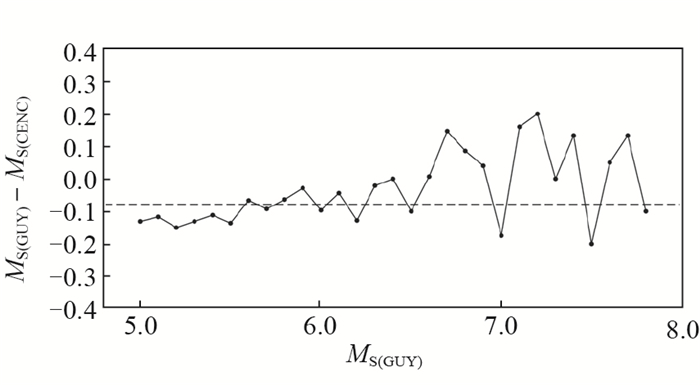
|
图 5 震级偏差与震级关系 Fig.5 Relationship between magnitude deviation and magnitude |
震级偏差与震级本身大小有关,这可能与震级公式中的周期校正项T有关,因为面波周期不仅是震中距的函数,还是震级的函数(訾少刚等,2006)。
4.3.2 震中距以20°为间隔,分析震级偏差与震中距关系,表 2为不同震中距范围内地震数和震级偏差平均值。由表 2可见:①各个震中距范围内,震级偏差平均值均为负;②当震中距大于60°时,震级偏差最大,为-0.10;③当震中距为0°—20°时,震级偏差最小,为-0.04。
| 表 2 震级偏差与震中距关系 Table 2 Relationship between magnitude deviation and epicentral distance |
随着震中距的增加,地震波传播所穿过的地下圈层变多,在地层中发生多次反射、折射,能量损失增大,从而造成波形记录失真,可能导致偏差变大。此外,面波震级公式中的起算函数是震中距的函数,而每个台站的起算函数是不一样的,中国地震台网中心统一正式报的震级结果,是多台计算的平均结果,此为造成偏差的原因之一。
4.3.3 震中方位以灌云台位置为坐标原点,将地震事件按4个方位划分,并计算其震级偏差平均值,结果见表 3。由表 3可知,东北方向震级偏差平均值最大,为-0.16;西南方向震级偏差平均值最小,为-0.01。这与区域地质构造情况有关,也与深部介质结构特征有关,因为介质路径不同,对地震波的固有吸收衰减和散射衰减是不同的(刘红桂,2012),直接影响了台站记录到的面波振幅大小,造成单台震级偏差。而中国地震台网中心的震级为多个台站的算术平均值,在一定程度上消除了方向性的影响(中国地震局监测预报司,2003)。
| 表 3 震级偏差与震中方位关系 Table 3 Relationship between magnitude deviation and epicenter orientation |
对灌云台2019—2021年698个地震事件进行统计,结果显示,远震事件震级集中在MS 5.0—7.0,灌云台面波震级比中国地震台网中心震级平均低0.08左右,说明灌云台远震记录稳定,映震能力强,平均误差小,记录精度较高,台站震级无需校正。
由震级偏差与震级大小的关系可知,当5.0≤MS≤6.5时,灌云台记录的震级偏差较小,震级较为准确,而当MS>6.5时,震级偏差开始变大;由震级偏差与震中距的关系可知,灌云台记录的震级精度随震中距的增加而减小;由震级偏差与震中方位的关系可知,灌云台记录到的东北方向和东南方向的地震震级偏差较大,可能与地震的海陆分布有关。
董海龙, 陈彦平, 雷功明, 等. 安西地震台数字记录面波震级偏差分析[J]. 高原地震, 2015, 27(4): 32-35. |
郭履灿, 庞明虎. 面波震级和它的台基校正值[J]. 地震学报, 1981, 3(3): 312-320. |
何奕成, 秦磊, 立凯, 等. 连云港地震台面波震级偏差分析[J]. 地震地磁观测与研究, 2016, 37(6): 38-42. |
何奕成, 范小平, 赵启光, 等. 郯庐断裂带中南段地壳结构分段特征[J]. 地球物理学报, 2021, 64(9): 3164-3178. |
李惠智. 关于震级误差成因的初步分析[J]. 高原地震, 2009, 21(2): 46-47. |
刘红桂. 不同构造区固有吸收衰减和散射衰减相对强弱的对比研究[J]. 国际地震动态, 2012, 11061106(1): 31-32. |
刘仲韬, 宋晓煜, 朱振兴. 张家口地震台面波震级偏差分析[J]. 地震地磁观测与研究, 2021, 42(4): 45-50. |
罗伯特·安德森. 现代稳健回归方法[M]. 李丁, 译. 上海: 上海人民出版社, 2019: 47-51.
|
田文德, 胡俊明. 成都台数字地震仪测定震级偏差分析与校正[J]. 四川地震, 2012, 11061106(3): 20-23. |
吴微微, 苏金蓉, 魏娅玲. 四川数字测震台网震级偏差分析[J]. 地震地磁观测与研究, 2014, 35(3/4): 112-117. |
余腾, 朱益民, 王鑫, 等. 郯庐断裂带苏鲁交汇区b值时空特征研究[J]. 地球物理学进展, 2020, 35(6): 2134-2142. |
中国地震局监测预报司. 地震参数——数字地震学在地震预测中的应用[M]. 北京: 地震出版社, 2003: 9-10.
|
訾少刚, 赵宁, 李惠智, 等. 银川地震台CTS-1数字地震仪震级校正初探[J]. 地震地磁观测与研究, 2006, 27(3): 114-118. |
 2023, Vol. 44
2023, Vol. 44

