2) 中国三河 065201 河北省地震动力学实验室;
3) 中国银川 750001 宁夏回族自治区地震局;
4) 中国四川 625000 雅安市防震减灾服务中心
2) Hebei Key Laboratory of Earthquake Dynamics, Sanhe 065201, China;
3) Earthquake Agency of Ningxia Hui Autonomous Region, Yinchuan 750001, China;
4) Ya'an Earthquake Prevention and Disaster Reduction Service Center, Sichuan Province 625000, China
1679年发生的三河—平谷8级地震,是我国有地震记载以来,首都圈地区发生震级最大、破坏性最强、波及范围最广的一次地震(向宏发等,1988)。多数研究者认为:1679年的三河—平谷8级地震的发震断裂是夏垫断裂(马坊—夏垫断裂),并且夏垫断裂是一条切穿莫霍面的深大断裂(向宏发等,1988;嘉世旭等,1995;张先康等,2002;王椿镛等,2016)。由于三河—平谷地震区紧邻北京和天津,所以近年来地学学者们在夏垫断裂带开展了大量关于区域深部构造背景、深浅构造关系、断裂活动性和地球物理特征等方面的研究,并取得了大量的研究成果。特别是三河—平谷孕震区的构造格架、地质和地球物理特征一直是地学专家们关注的热点,如利用深地震方法探测研究三河—平谷地震区的地质构造(张先康等,2002);利用接收函数方法研究首都圈区域地壳厚度和泊松比分布(罗艳等,2008;王峻等,2009;宫猛等,2015);利用固定地震台站的地震目录和地电、地磁、地下流体及地形变观测资料研究三河—平谷地震区地球物理场特征(田优平等,2014)。
2016年防灾科技学院围绕三河—平谷8级地震区建设5个测震台站,形成一个小型区域遥测台网,不仅填补了廊坊北部辖区没有固定测震台站的空白(范秀丽等,2016),还成为夏垫断裂带上的专业固定地震观测网。其中,防灾科技学院地震台(下文简称防灾台)位于夏垫断裂下盘(北西盘),其余4个台站位于夏垫断裂上盘(东南盘)。本文利用防灾科技学院地震遥测台网观测数据,使用H—κ叠加方法(Zandt et al, 1995;Zhu et al, 2000)反演三河—平谷地震区的莫霍面深度和泊松比,探讨三河—平谷地震区地壳结构及物质组成,为研究该地震区的地壳结构、岩石性质、地震活动性、构造应力分布等提供依据。
1 区域地质背景从大地构造角度分析,本研究区域处于华北平原地震带和张家口—渤海地震带交接区域,多条断裂带在区域内相切相交(图 1)。区域内主要有北北东至北东方向的夏垫断裂和河西务断裂,以及北西西向的宝坻断裂(向宏发等,1988;张先康等,2002)。其中,夏垫断裂带是首都圈地区的隐伏活动断裂,也是大兴隆起和大厂坳陷的分界断裂(向宏发等,1988;张先康等,2002)。历史上,三河—平谷地震区的地震活动水平相对较高。中国地震台网中心目录显示,截至2021年12月31日,这一地区共发生19次地震,均为浅源地震,震源深度大多在5—25 km,其中4级以上地震有4次,最大为8级。地震活动主要沿夏垫断裂带分布,受制于区域断裂构造展布。

|
图 1 防灾科技学院地震遥测台网台站布设、构造背景以及历史地震分布(李正芳,2021) Fig.1 Distribution of the Seismic Network in the IDP, tectonic background and historical earthquakes (Li, 2021) |
远震地震波在传播过程中会经过地壳、地幔和地核,遇到不同界面还会发生折射与反射,产生各种折射波与反射波,因此具有传播路径长、穿透度深、震相丰富、波形持续时间长等特点。
远震P波的波形可以用式(1)表示
| $ \left\{\begin{array}{l} D_{\mathrm{V}}(t)=I(t) \times S(t) \times E_{\mathrm{V}}(t) \\ D_{\mathrm{R}}(t)=I(t) \times S(t) \times E_{\mathrm{R}}(t) \\ D_{\mathrm{T}}(t)=I(t) \times S(t) \times E_{\mathrm{T}}(t) \end{array}\right. $ | (1) |
其中,DV(t)、DR(t)和DT(t)分别是垂向、径向和切向的远震P波振幅;I(t)是仪器响应;S(t)是震源函数;E(t)是介质速度结构信息。
由于远震P波在台站下方近似于垂直入射,所以垂直分量的能量集中于直达P波,EV(t)可以用δ函数表示,即
| $ E_{\mathrm{V}}(t) \approx \delta(t), D_{\mathrm{V}}(t)=I(t) \times S(t) $ | (2) |
将式(1)—(2)通过傅里叶变换至频率域,则有
| $ \left\{\begin{array}{l} D_{\mathrm{V}}(\omega)=I(\omega) \times S(\omega) \\ D_{\mathrm{R}}(\omega)=I(\omega) \times S(\omega) \times E_{\mathrm{R}}(\omega) \\ D_{\mathrm{T}}(\omega)=I(\omega) \times S(\omega) \times E_{\mathrm{T}}(\omega) \end{array}\right. $ | (3) |
消除仪器响应因子I(ω)和震源函数因子S(ω)后,可得
| $ \left\{\begin{array}{l} E_{\mathrm{R}}(\omega) \approx \frac{D_{\mathrm{R}}(\omega)}{D_{\mathrm{V}}(\omega)} \\ E_{\mathrm{T}}(\omega) \approx \frac{D_{\mathrm{T}}(\omega)}{D_{\mathrm{V}}(\omega)} \end{array}\right. $ | (4) |
再次通过傅里叶变换将式(4)转为时间域,ER(t)和ET(t)即为径向和切向的接收函数。
| $ \left\{\begin{array}{l} E_{\mathrm{R}}(t) \approx \frac{D_{\mathrm{R}}(t)}{D_{\mathrm{V}}(t)} \\ E_{\mathrm{T}}(t) \approx \frac{D_{\mathrm{T}}(t)}{D_{\mathrm{V}}(t)} \end{array}\right. $ | (5) |
实际的地震信号是含有大量噪音的,且当垂直分量趋近于0时,频率域也会不稳定,因此在数据预处理时需要使用滤波器进行带通滤波消除干扰,引入水准量控制振幅水平。
| $ \left\{\begin{array}{l} E_{\mathrm{R}}(\omega) \approx \frac{D_{\mathrm{R}}(\omega) \bar{D}_{\mathrm{R}}(\omega)}{\phi(\omega)} G(\omega) \\ \phi(\omega)=\max \left(D_{\mathrm{V}}(\omega) \bar{D}_{\mathrm{V}}(\omega), c \cdot \max \left(D_{\mathrm{V}}(\omega) \bar{D}_{\mathrm{V}}(\omega)\right)\right) \\ G(\omega)=\mathrm{e}^{-\frac{\omega^{2}}{4 a^{2}}} \end{array}\right. $ | (6) |
式中,G(ω)是高斯滤波器;α是高斯滤波带宽因子,控制消除噪音频率;c是水准量,控制振幅水平,取值范围由实际情况决定,多选择在0.000 1—0.01之间;
在水平层状介质中,远震P波在莫霍面入射产生的多次转换震相Ps、PpPs、PsPs + PpSs等,通过给定地壳平均速度,即可得到Ps、PpPs、PsPs、PpSs等震相与直达P波震相的到时差tPs、tPpPs和tPsPs + PpSs:
| $ \left\{\begin{array}{l} t_{\mathrm{Ps}}=\frac{H}{V_{\mathrm{P}}}\left(\sqrt{\left(\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}\right)^{2}-p^{2} V_{\mathrm{P}}^{2}}-\sqrt{\left.1-p^{2} V_{\mathrm{P}}^{2}\right)}\right. \\ t_{\mathrm{PpPs}}=\frac{H}{V_{\mathrm{P}}}(\sqrt{\left(\frac{V_{\mathrm{P}}}{V_{\mathrm{S}}}\right)^{2}-p^{2} V_{\mathrm{P}}^{2}}+\sqrt{1-p^{2} V_{\mathrm{P}}^{2})} \\ t_{\mathrm{PsPs}+\mathrm{PpSs}}=\frac{2 H}{V_{\mathrm{P}}}\left(\sqrt{\left(\frac{V_{\mathrm{P}}}{V_{\mathrm{P}}}\right)^{2}-p^{2} V_{\mathrm{P}}^{2}}\right. \end{array}\right. $ | (7) |
式中,H是地壳厚度,VP是地壳内P波的平均速度,VS是地壳内S波的平均速度,p是射线参数。
在预设地壳模型下,通过叠加大量接收函数,便可以扫描出最优的平均莫霍面深度和波速比。
| $ S(H, \kappa)=\omega_{1} r\left(t_{\mathrm{Ps}}\right)+\omega_{2} r\left(t_{\mathrm{PpPs}}\right)-\omega_{3} r\left(t_{\mathrm{PsPs}+\mathrm{PpSs}}\right) $ | (8) |
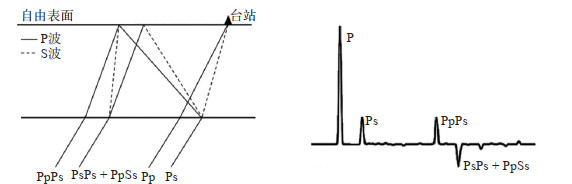
|
图 2 接收函数示意 Fig.2 Schematic diagram of receiver functions |
式(8)中,r(t)为径向接收函数,ωi(i =1, 2, 3)为相应震相的权重系数,且有Σωi = 1。当式(8)达到最大值时,说明各震相叠加能量也达到最大,各震相的到时最真实,此时H和κ也是最接近现实的结果。泊松比σ可以通过波速比κ计算得出,公式如下
| $ \sigma=\frac{1}{2}\left[1-\frac{1}{\kappa^{2}-1}\right] $ | (9) |
防灾科技学院地震遥测台网(图 1)各地震台间距约20 km,几何布局合理,其中防灾台和凌家吴台是宽频带台站,大朗台、安头屯台和大罗村台是短周期台站。宽频带台站采用TBS-60B井下宽频带地震计,观测系统的动态范围优于145 dB,观测频带60 s—50 Hz。短周期台站采用TBV-33S井下短周期地震计,观测系统的动态范围优于130 dB,观测频带2 s—50 Hz。地震数据采样率为100 Hz,地震台站采用GPS授时系统,时钟精度<0.1 ms。遥测台网自运行以来,观测环境无明显干扰,可提供高质量的地震波形资料供研究使用。
根据中国地震台网地震目录对防灾科技学院地震遥测台网2017年1月—2021年12月的观测数据进行筛选,挑选出震中距离介于30°—90°之间的高分辨率地震记录数据。为提高计算结果的精度,以波形记录中原始P波垂直分量记录清晰、信噪比高且震级MS≥5.5为条件继续进行筛选,并人工对备选远震事件波形进行P波标注;然后截取P波到时前10 s至到时后55 s的地震波形,并进行去均值、去倾斜和butterworth带通滤波等预处理;最后将地震波形数据由原始的N—E—Z三分量旋转到R—T—Z分量,利用时间域迭代反褶积方法(Ligorría et al, 1999)提取P波接收函数,并以拟合度≥90%为原则挑选信噪比较高的接收函数用于后续计算。最终从5个地震台合计筛选出344条远震波形事件参与反演计算。远震事件分布如图 3所示,其方位覆盖较为完整。

|
图 3 远震事件分布 Fig.3 Distribution of teleseismic events |
参考Crust1.0全球模型以及嘉世旭等(2005)给出的人工地震测深结果,设平均地壳速度为6.1 km/s,高斯滤波因子α为2.5,搜索地壳厚度H的范围为20—50 km,搜索波速比κ的范围为1.5—2.0,震相Ps、PpPs、PsPs + PpSs的权重分别为0.7、0.2和0.1,地壳厚度和波速比的搜索步长分别为0.1和0.001,进行H—κ叠加,最终得到防灾地震遥测台网5个台站下方的莫霍面深度和波速比(表 1)。
| 表 1 三河—平谷地震区莫霍面深度和泊松比 Table 1 Moho depth and Poisson's ratio inthe Sanhe-Pinggu earthquake area |
由表 1可知,每个台站地壳厚度误差均小于0.5 km,波速比误差小于0.01,说明本次研究结果比较稳定可靠。
3.3 计算示例图 4是防灾台的计算过程示例。由图 4(a)和图 5(b)可知,接收函数的震中距和反方位角分布较好。图 4(b)是防灾台的H—κ扫描结果,即当H为41.0 km,κ为1.71时,式(8)的S(H,κ)达到最大极值,由此可得防灾台下方的地壳厚度为41.0 km,波速比为1.71。
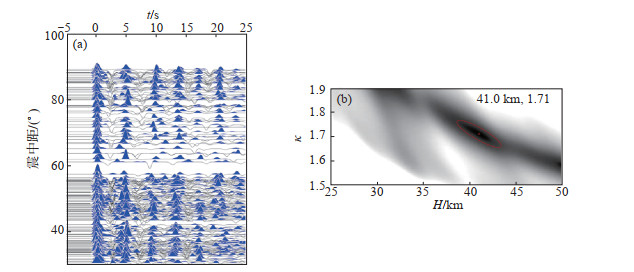
|
图 4 防灾台接收函数及H—κ叠加反演结果 (a)接收函数(以震中排列);(b) H—κ叠加结果 Fig.4 Receiver functions and H-κ stacking inversion results at stations of IDP |

|
图 5 接收函数(以反方位角排列) (a)理论接收函数;(b)防灾台实际接收函数 Fig.5 Receiver functions (arranged in reverse azimuth) |
为了验证反演结果的可靠性,设莫霍面倾向为0°,倾角搜索范围为0°—20°,地壳平均P波速度为6.1 km/s,上地幔顶部P波速度为8.1 km/s(赵金仁等,1999;徐锡伟等,2002;嘉世旭等,2005),正演计算理论接收函数,如图 5(a)。通过与本文计算的实际接收函数图 5(b)相对比,可以看出实际接收函数与理论接收函数中的P、Ps、PpPs、PsPs + PpSs震相的拟合程度较好,说明本研究反演结果是可靠的。
由于研究区地处潮白河冲洪积扇区域,所以接收函数(图 4)受第四纪松散覆盖层影响,不仅在初至P波到时1 s前后出现一组介于P和Ps波的转换震相,还存在多次转换波。
4 分析与讨论 4.1 莫霍面深度图 6是三河—平谷地震区莫霍面深度图。由图 6和表 1可知,三河—平谷地震区的平均莫霍面深度约37.06 km,与华北地区深部构造展布及其变化规律相吻合,其地壳厚度由西向东、由北向南逐渐变薄。从燕郊向东延伸至大厂方向存在一个坳陷区,这与区域地质资料相符。莫霍面深度与Crust1.0全球地壳模型31—38 km、重力反演34—36 km(姜文亮等,2012;张明辉等,2020)、深震探测33—37 km(向宏发等,1988;嘉世旭等,1995;张先康等,2002;王椿镛等,2016)和根据接收函数(罗艳等,2008;王峻等,2009;宫猛等,2015)所得研究结果较为一致。其中凌家吴台站下方地壳最厚,达到41.10 km,大罗台下方地壳最薄,为31.70 km,两台厚度差达到9.40 km。结合张先康等(2002)人工地震资料,认为研究区域存在一个地壳陡变带,呈北东走向。
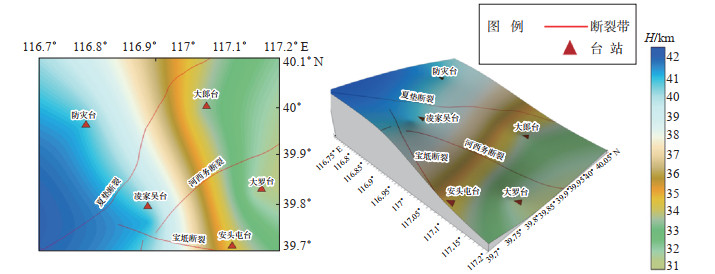
|
图 6 三河—平谷地震区莫霍面深度和形态 Fig.6 Moho depth and morphology in the Sanhe-Pinggu earthquake area |
根据泊松比与波速比的关系[式(9)],通过H—κ叠加反演的波速比计算出研究区域的泊松比值为0.240—0.303(图 7),平均值0.276 4,极差0.071,与王峻等(2009)在本区域研究结果基本一致。
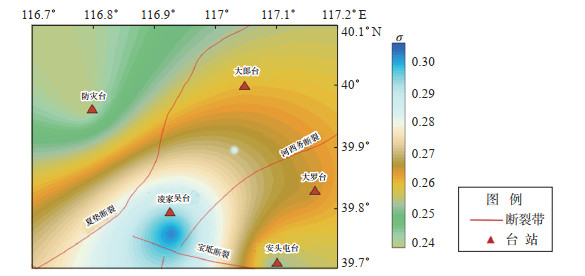
|
图 7 三河—平谷地震区的泊松比 Fig.7 Poisson's ratio in the Sanhe-Pinggu earthquake area |
目前,大陆地壳物质的泊松比值变化范围多在0.20—0.35(Holbrook et al, 1992;Christensen,1996)。地壳物质为酸性的泊松比值小于0.26(σ≤0.26),以长英质矿物含量高的居多;泊松比值在0.26—0.28(0.26<σ≤0.28),地壳物质呈中性,中性矿物或酸性岩和基性岩等比例共生;泊松比值在0.280—0.30(0.28<σ≤0.30),地壳物质以铁镁质矿物含量高的居多;泊松比值大于0.30(σ>0.3),则下方更有可能出现部分熔融或存在高孔隙度的破碎带(嵇少丞等,2009)。从图 7中可以看出,三河—平谷地震区泊松比分布与夏垫断裂带展布有关。高泊松比的区域主要集中在夏垫断裂上盘,且此区域地热资源丰富,水温在40 ℃—62 ℃,地下热水年可采资源量达1 282×104 m3(张嵩月,2016;张进平等,2018)。根据地壳物质成分与泊松比之间的关系推断:由于夏垫断裂带是一条贯穿至莫霍面的深断裂,上地幔物质上涌造成了区域泊松比的差异。在华北克拉通伸展减薄的大背景下,地幔物质上涌侵入下地壳,其高温熔融了部分火成变质岩形成壳内低速体。研究区域的煤层中有辉绿岩脉和煌斑岩脉侵入,在部分区域有玄武岩出露(张嵩月,2016),也表明研究区域曾发生过基性岩浆底层侵入活动。低泊松比区域则有可能出现了拆沉作用。
综合分析莫霍面深度和泊松比,可以得到区域大陆地壳构造演化变形是碰撞增厚还是伸展减薄,是否存在壳幔物质交换等信息。三河—平谷地震区的莫霍面深度和泊松比呈负相关,即随着莫霍面深度的降低,泊松比值升高。由此推测:在华北克拉通构造拉伸作用的背景下,随着莫霍面深度的降低,深大断裂带即夏垫断裂带的压力骤减,上地幔物质发生底侵作用,侵入部分不仅抵消了上地壳的亏损,还增加地壳厚度和泊松比。这不仅与华北地区的实际情况相符,也与张先康等(2002)通过深地震反射探测法得到的夏垫断裂带是一条贯穿莫霍面深断裂的相关研究成果相吻合。
5 结论通过对防灾科技学院地震遥测台网5个地震子台的远震P波资料进行分析,利用H—κ叠加方法,得到三河—平谷地震区下方的莫霍面深度和泊松比,分析该地震区莫霍面深度和泊松比变化特征,得出以下结论:
(1)防灾遥测地震台网的接收函数信噪比高,关键震相清晰,反演得到的莫霍面深度及泊松比结果可靠。
(2)三河—平谷地震区的莫霍面深度在31.70—41.10 km之间,平均值为37.06 km,莫霍面深度变化幅度较大(极差9.40 km),地壳呈西厚东薄的特征,与华北地区发生构造伸展的实际情况相契合。研究区域内莫霍面深度呈块状分布特征,与区域内断裂构造相关。
(3)三河—平谷地震区的泊松比分布在0.240—0.303之间,变化较为复杂,高泊松比区域集中在夏垫断裂带上盘,应与夏垫断裂是一条深切地壳的断裂带有关,说明研究区域东南向主要呈现为构造上的拉张伸展特征,而西北向呈现出挤压特征。
(4)莫霍面深度与泊松比之间呈负相关,即泊松比随着莫霍面深度降低而升高。推测在华北地区地壳伸展背景下,由于夏垫断裂带是一条深大断裂,受岩浆底侵作用,幔源物质进入地壳,造成莫霍面抬升,泊松比值升高。
(5)基于H—κ叠加方法获取的地壳厚度及波速比结果,对地壳厚度和波速比扫描范围较敏感,且不同的高斯滤波因子也会引起小幅变化。对于小区域或精细结构研究,这种变化幅度不可忽视。在使用H—κ叠加方法时,地壳平均波速VP、地壳厚度H和波速比κ尽量选取研究区域人工地震测深和重力观测结果进行约束,以保证反演结果的合理性。
范秀丽, 郑美杰, 林建慧, 等. 廊坊市地震台站现状及创新发展机制探索[J]. 国际地震动态, 2016(11): 22-27. |
宫猛, 李信富, 张素欣, 等. 利用接收函数研究河北及邻区地壳厚度与泊松比分布特征[J]. 地震, 2015, 35(2): 34-42. |
嵇少丞, 王茜, 杨文采. 华北克拉通泊松比与地壳厚度的关系及其大地构造意义[J]. 地质学报, 2009, 83(3): 324-330. |
嘉世旭, 刘昌铨. 华北地区人工地震测深震相与地壳结构研究[J]. 地震地质, 1995, 17(2): 97-105. |
嘉世旭, 齐诚, 王夫运, 等. 首都圈地壳网格化三维结构[J]. 地球物理学报, 2005, 48(6): 1 316-1 324. |
姜文亮, 张景发. 首都圈地区精细地壳结构——基于重力场的反演[J]. 地球物理学报, 2012, 55(5): 1 646-1 661. |
李正芳, 李彦宝, 周本刚, 等. 北京平原大兴凸起东缘断裂全新世活动的新认识[J]. 地震地质, 2021, 43(6): 1 671-1 681. |
罗艳, 崇加军, 倪四道, 等. 首都圈地区莫霍面起伏及沉积层厚度[J]. 地球物理学报, 2008, 51(4): 1 135-1 145. |
田优平, 余达远, 万永革, 等. 三河-平谷地震区地球物理特征研究[J]. 地球物理学进展, 2014, 29(4): 1 563-1 572. |
王椿镛, 段永红, 吴庆举, 等. 华北强烈地震深部构造环境的探测与研究[J]. 地震学报, 2016, 38(4): 511-549. |
王峻, 刘启元, 陈九辉, 等. 首都圈地区的地壳厚度及泊松比[J]. 地球物理学报, 2009, 52(1): 57-66. |
向宏发, 方仲景, 徐杰, 等. 三河-平谷8级地震区的构造背景与大震重复性研究[J]. 地震地质, 1988, 10(1): 15-28. |
徐锡伟, 吴卫民, 张先康, 等. 首都圈地区地壳最新构造变动与地震[M]. 北京: 科学出版社, 2002.
|
张进平, 袁利娟. 夏垫断裂带对地热资源分布的影响——以通州西集地区为例[J]. 城市地质, 2018, 13(3): 15-20. |
张明辉, 申重阳, 吴桂桔, 等. 三河-平谷8.0级地震区浅层三维密度结构反演研究[J]. 大地测量与地球动力学, 2020, 40(11): 1 112-1 117. |
张嵩月. 河北省三河市地热地质研究与地下热水资源开发前景评价[D]. 北京: 中国地质大学(北京), 2016.
|
张先康, 赵金仁, 刘国华, 等. 三河-平谷8.0级大震区震源细结构的深地震反射探测研究[J]. 中国地震, 2002, 18(4): 326-336. |
赵金仁, 张先康, 张成科, 等. 香河-北京-涿鹿及其相邻地区壳幔构造与速度结构特征[J]. 地震地质, 1999, 21(1): 29-36. |
Christensen N I. Poisson's ratio and crustal seismology[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B2): 3 139-3 156. |
Holbrook W S, Mooney W D, Christensen N I. The seismic velocity structure of the continental crust[M]//Fountain D M, Arculus R J, Kay R D. The Continental Lowercrust. Amsterdam: Elsevier, 1992.
|
Ligorría J P, Ammon C J. Iterative deconvolution and receiver-function estimation[J]. Bulletin of the Seismological Society of America, 1999, 89(5): 1 395-1 400. |
Zandt G, Ammon C J. Continental crust composition constrained by measurements of crustal Poisson's ratio[J]. Nature, 1995, 374(6 518): 152-154. |
Zhu L P, Kanamori H. Moho depth variation in southern California from teleseismic receiver functions[J]. Journal of Geophysical Research: Solid Earth, 2000, 105(B2): 2 969-2 980. |
 2023, Vol. 44
2023, Vol. 44


