海潮是海洋表面受到太阳和月亮引力后产生的周期性涨落现象,其与重力固体潮具有同源性,会产生相同的频谱特征,因此在观测的重力固体潮资料中会夹杂海潮信息(焦新华等,2009)。分析重力固体潮汐残差信号可获得地球内部动力学信息,但其中夹杂的全球和局部海潮负荷对分析结果影响较大,仅采用滤波法难以将其剔除,尤其在沿海地区,海潮负荷对重力潮汐振幅占比更大(杜文成等,2018)。为了更加有效地利用重力观测资料精密测定地球潮汐常数并研究地核运动等问题,对重力观测资料进行海潮负荷信号改正尤为重要(孙和平等,2002)。
佘山地震监测中心站(下文简称佘山台)位于上海市西南郊佘山脚下,现有地震、地磁、重力、形变、流体等地球物理观测手段。佘山台2000年配备DZW重力仪进行重力观测,2014年5月完成重力仪数据采集器的升级改造,并完善相关辅助观测记录,增加重力仪秒钟值连续记录。改造完成后,重力仪工作记录稳定,数据连续率、完整率提高。重力仪采样周期提高后,基于潮汐观测的震前变化信息得以丰富(叶青等,2020)。该台地处沿海,重力固体潮汐观测受海潮负荷影响较大,采用Eterna3.30(Wenzel,1996)标准潮汐分析软件,基于全球海潮模型,对该台2020年1月—2021年10月重力数据进行海潮负荷改正效应分析,得到该台重力观测海潮负荷特征,以期提高重力固体潮观测有效性。
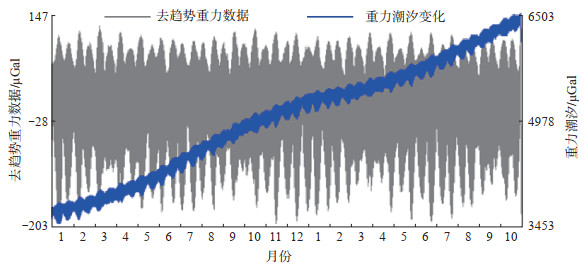
1 数据选取选取2020年1月至2021年10月佘山台连续重力整点值数据(原始采样率为1 Hz),利用T-soft(Van Camp et al,2005)软件,采用插值方法,对仪器故障、断电等数据进行间断处理,剔除地震同震响应、尖峰、仪器掉格、突跳等数据。因仪器恒温系统故障,2021年10月29日重力数据曲线异常,此后至12月的数据予以剔除,因此截取2020年1月1日至2021年10月28日的连续重力数据进行分析,预处理数据曲线见图 1。
|
图 1 2020年1月1日至2021年10月28日佘山重力潮汐变化及去趋势重力数据曲线 Fig.1 Tidal variation gravity data and detrending gravity data of Sheshan station in 2020.1.1 to 2021.10.28 |
采用Eterna3.30(Wenzel,1996)标准潮汐分析软件,对佘山台重力仪预处理整点值数据进行固体潮汐调和分析,计算半日潮波M2、S2、K2、N2和周日潮波O1、K1、P1、Q1的振幅因子、相位滞后和误差估算参数,结果见表 1。其中,O1、K1、M2、S2波振幅(K1波为47.549 8 μGal、O1波为35.039 7 μGal、M2波为63.837 8 μGal、S2波为29.634 6 μGal)较大,表明4种潮波受海潮影响较大;8个主波振幅因子中误差均在1%以内,表明佘山台重力观测数据精度较高;除Q1波外,M2、S2、K2、N2、K1、P1、Q1波均存在相位滞后。下文将参考杨锦玲等(2016)、翟丽娜等(2021)的研究,采用振幅较大的O1、K1和M2波,对佘山台连续重力数据进行海潮负荷效应分析。
| 表 1 佘山台重力仪潮汐实测结果 Table 1 Tidal observation results of gravimeter at Sheshan station |
全球现代化海潮模型有同化模型和经验模型2种,其中经验模型是对卫星测高数据进行潮汐信息提取而成,同化模型是在流体动力学模型基础上对各类观测数据同化后形成。选取8个全球海潮模型,对佘山台连续重力数据进行海潮负荷效应计算。目前,全球海潮模型分辨率和精度不断提高,但由于佘山台所在地区地处近海,海潮梯度变化大,基于全球海潮模型在对我国近海区域进行计算时,结果可能存在一定误差。所选海潮模型信息见表 2。
| 表 2 海潮模型信息 Table 2 Ocean tide model information |
在计算海潮负荷效应时一般使用傅里叶经验负荷理论(Farrell,1972),并采用Agnew(1997)提出的积分格林函数法,将海潮与重力格林函数进行褶积积分,计算公式如下
| $ \begin{gathered} L(\theta, \lambda, t)=a^2 \iint \rho H\left(\theta^{\prime}, \lambda^{\prime}, t^{\prime}\right) \cdot G(\varphi) S(A) \sin \theta^{\prime} \mathrm{d} \theta^{\prime} \mathrm{d} \lambda^{\prime}= \\ a^2 \iint \rho H(\theta, \lambda, t) G(\varphi) S(A) \sin \varphi \mathrm{d} \varphi \mathrm{d} A \end{gathered} $ | (1) |
式中,L(θ, λ, t)为某地某时刻的海潮负荷,其中t为时间,θ和λ为计算点的余纬和经度;a为地球半径;ρ为海水密度;H(θ', λ', t')为瞬时潮高,其中θ'和λ'为负荷点的余纬和经度;G(φ)为与角距有关的重力负荷格林函数,可由负荷勒夫数h和k的组合求得。
基于公式(1),在8种全球海潮模型下,计算得到佘山台重力数据中受海潮影响最大的O1、K1、M2潮波的海潮负荷信息,统计结果见表 3。
| 表 3 佘山台重力仪记录的O1、K1、M2潮波海潮负荷信息 Table 3 Ocean tide load information of tidal waves O1, K1, M2 of gravimeter at Sheshan station |
由表 3可知,在8个海潮模型下,O1、K1、M2波振幅平均值大于1.2 μGal,分别为1.227 μGal、1.569 μGal和2.097 μGal,重力海潮负荷振幅分布在4.6—5.4 μGal。
对于在半日潮波频段的M2波,基于GOT4.8模型计算的振幅值最大,达2.294 μGal,约为观测振幅的3.6%,而基于FES2004模型的振幅值最小,为1.896 μGal,约为观测振幅的3.0%。对于在周日潮波频段的O1波,在NAO99b模型下振幅值最大,达1.419 μGal,约为观测振幅的4.0%,而在EOT11a模型下振幅最小,为1.162 μGal,约占观测振幅的3.3%。K1波的最大振幅值在NAO99b模型下计算得出,为1.818 μGal,约占观测振幅的3.8%,其最小振幅在EOT11a模型下计算得到,为1.471 μGal,约占观测振幅的3.1%。可见,在8种海潮模型下,计算结果差异不大,侧面说明佘山台海潮负荷对重力的影响不容忽视,需要进行海潮改正。
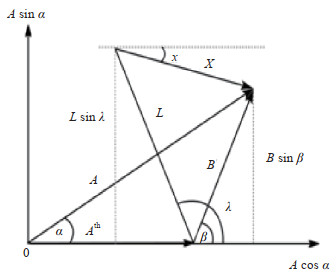
2.2 海潮负荷改正为研究海潮负荷影响,将重力负荷中3个主潮波信息,即O1、K1、M2波进行矢量计算。如图 2所示,引入一个剩余残差矢量Ath,表示固体潮理论值,矢量A为固体潮观测值,矢量L为海潮负荷(相位、振幅分别为λ和L),矢量B为固体潮观测残差,矢量X表示固体潮剩余残差(相位、振幅分别为χ和X),α、β、λ为重力海潮负荷3个主潮波的矢量角。其中A、B、X、L有如下关系
|
图 2 重力固体潮海潮负荷改正矢量图 Fig.2 Vector diagram of ocean tide load correction for gravity solid tide |
| $ \boldsymbol{B}=\boldsymbol{A}-\boldsymbol{A}^{\text {th }} \quad \boldsymbol{X}=\boldsymbol{B}-\boldsymbol{L} $ | (2) |
固体潮观测值振幅和振幅因子分别为A和δ,理论振幅和振幅因子分别为Ath、δth,四者之间具有以下关系
| $ \frac{A}{\delta}=\frac{A^{\text {th }}}{\delta^{\text {th }}} $ | (3) |
经海潮改正后,剩余残差振幅X和相位χ的计算公式如下
| $ \begin{aligned} & X=B^2+L^2-2 B L \cos (\beta-\lambda) \\ & \chi=\tan ^{-1}[(B \sin \beta-L \sin \lambda) /(B \cos \beta-L \cos \lambda)] \end{aligned} $ | (4) |
采用8个全球海潮模型对佘山台重力数据进行海潮负荷改正计算,文中给出振幅较大的O1、K1和M2波计算结果,见表 4,可知3种波的观测残差值分别为2.084 μGal、2.194 μGal和3.070 μGal,经海潮模型改正后三者剩余残差数值范围差别不大,分别为0.886—0.917 μGal、0.503—0.727 μGal和3.996—4.691 μGal,其中:周日波O1波和K1波的剩余残差与观测残差相比有较大幅度的减小;而半日波M2波剩余残差经海潮改正虽略有增大,但与倾斜固体潮海潮负荷改正结果(周江存等,2006)一致,结合观测值和理论振幅因子的计算结果,认为可能与未进行区域海潮模型改正或佘山台区域地质构造等有关,也可能是因为,数据处理流程和手段需要改进,或者佘山台重力记录中M2波不适合做海潮负荷改正。后续可考虑利用区域海潮模型,剔除大气负荷效应和台站区域地质构造等因素对重力仪观测数据的影响,对该台重力数据进行深入分析。
| 表 4 佘山台重力观测残差和剩余残差 Table 4 Error and residual error of gravity observation at Sheshan station |
将O1、K1和M2波振幅进行全球海潮模型改正,将所得振幅因子与观测值和理论值进行对比,发现:除M2波,O1、K1波振幅因子有一定程度的减小,且相较观测值更趋近于理论值,与理论值之间的差异由改正前的4%—6%降低到2.5%以内(表 5),说明了海潮模型改正的有效性;M2波振幅因子理论值与观测值差异较小,可能与未考虑区域海潮模型有关,仅利用全球海潮模型进行改正,导致数据失真。
| 表 5 观测振幅因子和海潮改正后的振幅因子 Table 5 Observed amplitude factor and amplitude factor after ocean tide correction |
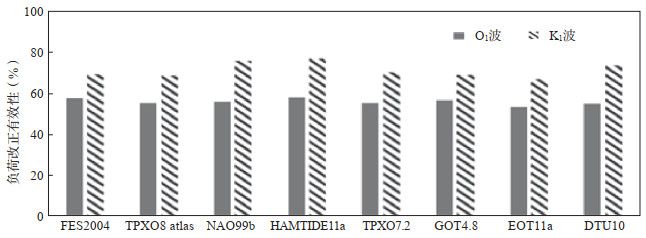
为更好地反映海潮负荷改正效果,采用“负荷改正有效性”(孙和平等,2006)方法,即观测残差矢量振幅减去最终残差振幅后除以观测残差振幅,用以综合评价主要潮汐波负荷改正的有效性。因M2波海潮改正存在失真,文中仅对O1和K1波海潮负荷有效性进行分析。图 3给出O1和K1波在8种海潮模型下负荷改正的有效性统计,可见:O1波的海潮负荷改正有效性差异不大,其中HAMTIDE 11a模型的有效性最高,EOT11a模型的有效性最低,分别为58.11%和53.41%;K1波的海潮负荷改正效果更佳,平均有效性达71.27%,但各模型存在一定差异,其中HAMTIDE 11a模型有效性最高(数值为77.07%),EOT11a模型有效性最低(数值为66.86%),二者差异达10.21%。
|
图 3 8个海潮模型对O1和K1波的负荷改正有效性 Fig.3 Loading correction efficiency of O1 and K1 calculated by 8 different ocean tide models |
结合表 5和图 3可知,O1和K1波在HAMTIDE 11a海潮模型下的负荷改正效果最佳。通过负荷改正有效性,直观可见佘山台重力数据经不同海潮模型的负荷改正后,仍存在较大剩余残差,也反映出全球海潮模型对该台重力数据的影响与其他地区存在一定差异。
3 结论采用佘山台重力观测数据,基于8个全球海潮模型,计算并分析O1、K1和M2波的海潮负荷效应,通过海潮改正结果,对比分析不同海潮模型在该台重力观测中的适用性,得出以下结论:
(1)经数据预处理,发现佘山台重力观测数据中3个主潮波O1、K1和M2的潮汐因子中误差较小,数据记录精度高。
(2)在8个全球海潮模型下,O1、K1和M2波振幅平均值均大于1.2 μGal,重力海潮负荷的振幅分布在4.6—5.4 μGal。
(3)在8个全球海潮模型下,主要潮波O1、K1和M2的海潮负荷振幅差异不大,其中M2波振幅最大,O1和K1波振幅则略小。
(4)经海潮模型改正后,相较观测残差,周日波O1和K1剩余残差有较大幅度的减小,半日波M2波剩余残差则略有增大,说明M2波受非潮汐因素影响较大。结合振幅因子计算结果,可考虑利用区域海潮模型,并剔除大气负荷效应和台站区域地质构造等因素的影响,对佘山台重力观测数据进行深入分析。
(5)计算O1和K1波在8种全球海潮模型下的负荷改正有效性,可知O1波有效性为55.90%,K1波为71.27%,且不同模型对O1波的改正差异较小,对K1波改正效果更佳,结合海潮改正振幅因子分析,发现HAMTIDE 11a模型对O1和K1波的海潮改正效果最佳。
杜文成, 袁林果, 张宁宁, 等. 青岛台站重力固体潮和海潮负荷特征研究[J]. 大地测量与地球动力学, 2018, 38(9): 913-916. |
焦新华, 吴燕冈. 重力与磁法勘探[M]. 北京: 地质出版社, 2009: 16-17.
|
孙和平, 周江存. 中国地壳运动观测网络基准站重力场变化的海潮负荷信号改正问题[J]. 地球科学进展, 2002, 17(1): 39-43. |
孙和平, 许厚泽, 陈武, 等. 香港地区重力固体潮和海潮负荷特征研究[J]. 地球物理学报, 2006, 49(3): 724-734. DOI:10.3321/j.issn:0001-5733.2006.03.016 |
杨锦玲, 关玉梅, 钟继茂, 等. 厦门重力固体潮海潮负荷改正研究[J]. 地球物理学进展, 2016, 31(3): 992-998. |
叶青, 倪友忠, 方韬. 佘山地震台DZW重力仪同震响应特征分析[J]. 工程地球物理学报, 2020, 17(2): 190-197. DOI:10.3969/j.issn.1672-7940.2020.02.008 |
翟丽娜, 王松阳, 孔祥瑞. 海潮负荷对大连地震台重力固体潮的影响[J]. 地震地磁观测与研究, 2021, 42(2): 214-216. DOI:10.3969/j.issn.1003-3246.2021.02.069 |
周江存, 孙和平, 李正媛. 佘山台倾斜固体潮观测的海潮负荷改正[J]. 测绘学报, 2006, 35(1): 4-8. |
Agnew D C. NLOADF: A Program for Computing Ocean-Tide Loading[J]. J Geophys Res: Solider Earth, 1997, 102(B3): 5109-5110. DOI:10.1029/96JB03458 |
Farrell D E, Huebener R P, Kampwirth R T. Direct observation of growth of the landau domain structure[J]. Solid State Commun, 1972, 11(12): 1647-1649. DOI:10.1016/0038-1098(72)90762-4 |
Van Camp M, Vauterin P. Tsoft: Graphical and Interactive Software for the Analysis of Time Series and Earth Tides[J]. Comput Geosci, 2005, 31(5): 631-640. |
Wenzel H G. The Nanogal Software: Data Processing Package ETERNA 3.3[J]. Bull Inf Marees Terrestr, 1996, 124: 9425-9439. |
 2023, Vol. 44
2023, Vol. 44

