2) 中国乌鲁木齐 830011 新疆维吾尔自治区地震局;
3) 中国昆明 650224 云南省地震局
2) Earthquake Agency of Xinjiang Uygur Autonomous Region, Urumqi 830011, China;
3) Yunnan Earthquake Agency, Kunming 650224, China
地震烈度衰减关系是地震区划、地震灾害快速评估和地震安全性评价工作的前提和基础(王小龙等,2004),是描述烈度随震级(或震中烈度)和距离等变化的统计规律(王晓军等,2012)。经多年研究积累,地震工程领域建立了诸多震级—烈度衰减关系模型,其中椭圆烈度衰减关系模型应用较多,其源于历史震例统计,具有一定合理性,在一些地震研究工作中取得了较好的结果(陈达生等,1989;汪素云等,2000;王继等,2008;张苏平等,2015)。在建立此类椭圆模型时,重点在于建立震级与烈度之间的关系,在数据处理过程中,无法全面考虑地震动各影响因素,结果可能产生较大偏差。随着测震技术的升级和强震观测资料的积累,获取了考虑多因素的地震烈度衰减关系的研究成果。
沈大开等(1987)建议用等效破裂长度代替破裂长度改进断层破裂烈度衰减模型,应用统计数据和唐山地震资料,证实该方法能较好地拟合实际等震线;周锡元等(1987)依据椭圆形等烈度线的统计结果,讨论中国东部和西部地区不同震中烈度或震级的地震的平均震源深度和断层破裂长度,提出适用于点源(以震源距为距离参数)和线源(以场地—破裂线最短距离或场地—破裂线两端点平均距离为距离参数)的烈度衰减关系;郁曙君(1993)基于椭圆烈度衰减关系模型建立烈度衰减关系,采用两步拟合法推导得到一种限头回归方法,对中国东部平原和西北部地区的烈度衰减关系进行研究;郑广芬等(1993)应用“误差向后传播算法”拟合地震烈度衰减关系,将地震烈度作为有序分类变量而非数值型连续变量来处理,对长、短半轴2个距离项同时拟合衰关系;常银辉(2012)搜集我国大陆地区1913—2010年54次MS≥6.5地震的烈度等震线资料,建立中国大陆地区“基于断层距的地震烈度衰减关系”;卢建旗等(2013)提出一种基于等震线面积和长轴半径的烈度衰减关系建立方法,并搜集我国38次6.0级及以上地震,对该研究提出的衰减关系进行验证,结果表明,基于等震线面积和长轴半径的衰减关系能够较好地拟合实际地震等震线的形状;郑韵(2015)根据中国大陆构造应力场分区,拟合不同震源机制解的烈度衰减关系。此外,聂高众等(2018)在历史统计数据支持下,以中国地震局正式发布的地震震级、震源深度为输入参数,收集整理1966—2013年215次MS>5.0地震,建立“极震区烈度快速评估模型”。该方法虽然将烈度衰减关系椭圆模型扩展到引入深度的烈度衰减关系模型,但仅考虑了极震区烈度、震级和震源深度的关系,未涉及各个烈度区及长短轴因素。本研究将在历史地震统计数据支撑下,探索建立考虑震源深度的全新的烈度衰减评估模型,模型变量不仅含有烈度、长短轴、震级,还引入“震源深度”这一新的变量,常用椭圆烈度衰减关系模型被拓展为加入震源深度的烈度衰减关系模型,探讨震源深度对烈度衰减关系模型的影响,以便提升地震烈度衰减关系的精准度和大震烈度分布的可信度。
1 震例资料选取我国地质构造复杂,沿用中国地震烈度区划图的做法,大致以105°E线为界,将中国大陆划分为东部和西部2个区(王继等,2008)。汪素云等(2007, 2008)在研究地壳内横波衰减及非弹性衰减品质因子时指出,我国大陆内部存在不同的衰减特征,并将中国西部细分为西南及西北2个子区域,东部细分为东北、华北及华中、华南地区2个子区域(汪素云等,2000)。其中西南地区包括四川、贵州、云南、西藏、重庆、广西;西北地区包括陕西、甘肃、青海、内蒙古(105°E线以西)、宁夏、新疆;将中国东部细分为东北、华北及华中、华南;东北、华北地区主要包括北京、天津、河北、山西、辽宁、吉林、黑龙江、山东、河南、内蒙古(105°E线以东)(崔鑫,2010);华中、华南地区主要包括上海、江苏、浙江、安徽、福建、江西、湖北、湖南、广东、海南(王继等,2008)。
1970年以来,我国积累了较为丰富和准确的震源深度分布资料(金星等,2013)。据统计,西部地区发震频率远高于东部地区,而东部地区地震则具有典型的低震级、高烈度震害特点,4.0—4.9级地震的震中烈度通常可达Ⅵ度(张苏平等,2015)。而且,在中国地震局抗震救灾指挥工作中,对于中国大陆地区发生的4.0级及以上地震,均需给出灾害损失的快速评估结果。因此,为了保证各烈度衰减关系研究中不同分区的震例充足,以我国大陆地区1970年以来发生的MS≥4.0地震为研究资料,并可准确地对烈度资料进行地理坐标配准和数字化,且震例需具有准确的震源深度数据。
基于以上挑选原则,共得到418个震例,其中西部震例314个,东部震例104个,震例数据主要来源于中国地震局有关资料汇编、官方网站及相关文献等(中国地震局震害防御司,1999;中国地震局监测预报司,2001;中国地震局震灾应急救援司,2010)。所选取的震例数据统计结果见表 1。
| 表 1 本研究所选震例统计 Table 1 Statistics of selected earthquakes in this study |
采用长轴可转向法(张方浩等,2016)测量长、短轴数据。对于历史地震中等震线不规则的,叠加每个地震的烈度分布、地形图和发震构造图,依据原始等震线进行补全,参考发震断层走向和地形条件,提取不同烈度区的长、短轴半径(张方浩等,2016)。
2.2 数据分布量取得到我国西部和东部地区等震线资料,其中烈度—震级—震源深度分布关系见图 1,震级—距离分布关系见图 2。

|
图 1 我国西部、东部地区等震线资料中震级—烈度—震源深度分布 (a)西部地区;(b)东部地区 Fig.1 Distribution of isoseismal data intensity-magnitude-focus depth in Western China and Eastern China |

|
图 2 我国西部、东部地区等震线资料震级—震中距分布 (a)西部地区;(b)东部地区 Fig.2 The magnitude-epicenter distance distribution of isoseismal data in Western China and Eastern China |
(1)西部地区地震:震级分布范围为4.0≤MS≤8.4,烈度分布范围为Ⅳ度≤I≤Ⅺ度,震中距范围为0≤R≤486 km。其中,西北地区震源深度分布范围为3 km≤H≤74 km,震中距范围为0≤R≤360 km;西南地区震源深度分布范围为5 km≤H≤41 km,震中距范围为0≤R≤486 km。
(2)东部地区地震:震级分布范围为4.0≤MS≤8.0,烈度分布范围为Ⅳ度≤I≤Ⅺ度,震中距范围为0≤R≤476 km。其中,东北、华北地区震源深度分布范围为6 km≤H≤36 km,震中距范围为0≤R≤405 km;华中、华南地区震源深度数据分布范围为4 km≤H≤32 km,震中距范围为0≤R≤476 km。
3 考虑震源深度的烈度衰减关系的选取与确定基于Estevad等(孟宪东等,1987)和卢建旗等(2013)的研究,建立基于震源深度影响的地震烈度衰减关系模型,即利用震源深度与震源距合成新的震源距参数,来表示地震烈度衰减关系模型,分别记为模型1和模型2。
3.1 模型1的选取与系数确定 3.1.1 模型1的选取根据Estevad等(孟宪东等,1987)研究,地面水平峰值加速度与地震震级和震源距具有以下关系
| $a_1=A_1 \mathrm{e}^{B_1 M}(R+C)^E$ | (1) |
式中,a1为水平峰值加速度;M为震级,R为震源距;A1、B1、C、E为常数。普遍认为:地面水平峰值加速度与地震烈度具有等效的物理含义。将式(1)中的峰值加速度改为烈度值(孟宪东等,1987),其长、短轴方向的衰减关系为
| $I=\mathrm{e}^{d_1+d_2 M_{\mathrm{s}}}\left(\sqrt{R^2+H^2}+C\right)^\beta$ | (2) |
代入震中距长、短轴数据,得
| $I=\mathrm{e}^{d_1+d_2 M_{\mathrm{S}}}\left(\sqrt{a^2+H^2}+C\right)^\beta$ | (3) |
| $I=\mathrm{e}^{d_1+d_2 M_{\mathrm{S}}}\left(\sqrt{b^2+H^2}+C\right)^\beta$ | (4) |
式中:I为观测点烈度;H为震源深度;a为半长轴;b为半短轴;MS为面波震级,d1、d2、C、β为常数。
3.1.2 系数确定应用最小二乘法进行统计回归,得到基于模型1的分区地震烈度衰减关系回归系数,拟合结果见表 2。
| 表 2 模型1的系数拟合结果 Table 2 Coefficient fitting results of model 1 |
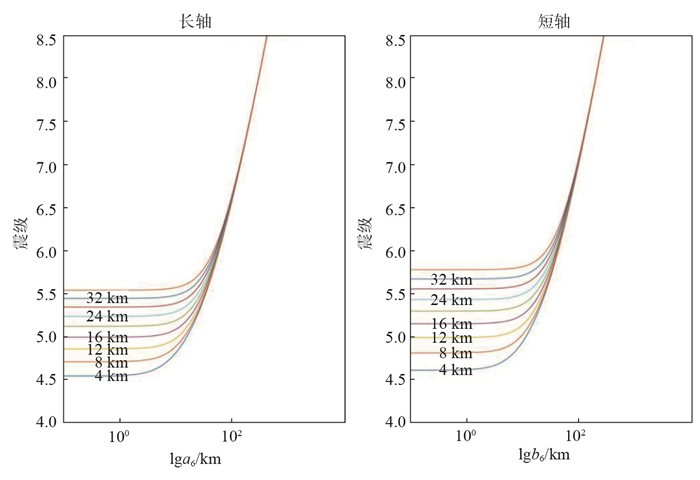
(1)我国东部地区地震震源深度对Ⅵ度(6度)区长短轴半径的影响。将表 2中我国东部地区模型1的拟合系数代入式(3)、式(4),分析该区不同震中距地震的震源深度对Ⅵ度(6度)区长短轴半径的影响。烈度值为6度,以长、短半轴的对数为横坐标,震级为纵坐标,震源深度设为4 km≤H≤36 km,绘制在不同震源深度影响下震级与长短轴的关系图,结果见图 3(图中震源深度间隔4 km)。
|
图 3 基于模型1的我国东部地区地震震源深度对Ⅵ度(6度)区长短轴半径的影响 Fig.3 The influence of focal depth in Eastern China on the radius of the major and minor axis of the six-degree area based on model 1 |
由图 3可见,震源深度参数对长轴的影响如下:震源深度H在4—36 km范围内,若震中距R在0—10 km,当4.5≤MS≤5.5时,模型1的衰减作用几乎不存在;若震中距R在10—100 km,当4.5≤MS≤5.5时,曲线斜率逐渐增大,模型1的衰减作用逐渐加快;到达中、远场范围,当震中距R>100 km、MS>5.5时,各曲线逐渐汇成一条曲线。也就是说,对于长轴模型来说,当10 km≤R≤100 km、4.5≤MS≤5.5时,若震源深度H在4—36 km范围内,其对模型1的影响作用逐渐增大,直至H>36 km、MS>5.5、R>100 km时,震源深度参数对模型1长轴的影响作用基本消失。
同理,震源深度参数对短轴的影响如下:震源深度H在4—36 km范围内,若震中距R在0—10 km,当4.6≤MS≤5.8时,模型1的衰减作用几乎不存在;若震中距R在10—100 km,在相同的震源深度和震级范围内,曲线斜率逐渐增大,衰减作用逐渐加快,直到在中、远场范围,即R>100 km、MS>5.8时,各曲线逐渐汇合成为一条曲线。也就是说,对于短轴模型来说,当10 km≤R≤100 km、4.6≤MS≤5.8时,若震源深度H在4—36 km范围内,其对模型1的影响作用逐渐增大,直至H>36 km、MS>5.8、R>100 km时,震源深度参数对模型1短轴的影响作用基本消失。
(2)我国西部地区地震震源深度对Ⅶ度(7度)区长短轴半径的影响。同理,将表 2中我国西部地区模型1的拟合系数代入式(3)、式(4),分析该区不同震中距地震的震源深度对7度区长短轴半径的影响。烈度值为7度,以长、短半轴的对数为横坐标,震级为纵坐标,设震源深度为4 km≤H≤36 km,绘制在不同震源深度影响下震级与长短轴的关系图,结果见图 4(图中震源深度间隔4 km)。

|
图 4 基于模型1的我国西部地区地震震源深度对Ⅶ度(7度)区长短轴半径的影响 Fig.4 The influence of focal depth in Western China on the radius of the long and short axis of the seven-degree area based on model 1 |
由图 4可见,震源深度参数对长轴的影响如下:H在4—36 km时,若R为0—10 km、5.2≤MS≤6.4,模型1的衰减作用几乎不存在;若R在10—100 km,在相同的震源深度和震级范围内,曲线斜率逐渐增大,衰减作用逐渐加快,直到在中、远场范围,即R>100 km、MS>6.4时,各曲线逐渐汇合成为一条曲线。也就是说,对于长轴模型来说,H在4—36 km范围内,若R在10—100 km、5.2≤MS≤6.4,该模型的影响作用逐渐增大,直至H>36 km、MS>6.4、R>100 km时,震源深度参数对模型1长轴的影响作用基本消失。
同理,震源深度参数对短轴的影响如下:H在4 km≤H≤36 km时,若R为0—10 km、5.2≤MS≤6.7,模型1的衰减作用几乎不存在;当R在10—100 km,在相同的震源深度和震级范围内,曲线斜率逐渐增大,衰减作用逐渐加快,直到在中、远场范围,即R>100 km、MS>6.7时,各曲线逐渐汇合成为一条曲线。也就是说,对于短轴模型来说,H在4—36 km范围内,若R在10—100 km、5.2≤MS≤6.4,震源深度参数对该模型的影响作用逐渐增大,直至H>36 km、MS>6.7、R>100 km时,震源深度参数对模型1短轴的影响作用基本消失。
3.2 模型2的选取与系数确定 3.2.1 模型2的选取烈度与震级、距离以及震源深度之间的经验关系一般是在“烈度与地震动场的能流密度成对数线性关系”假设的基础上建立起来的(卢建旗等,2013),如公式所示
| $I=k_1+k_2 \ln E$ | (5) |
式中,k1和k2为常量,E为烈度所在场地处的能流密度。其中能量衰减公式如下
| $E=\left(\frac{E_0}{4 \pi}\right) \varDelta^{-b} \mathrm{e}^{-c \varDelta}$ | (6) |
式中,E0为一次地震释放的总能量;b代表几何扩散衰减项;c代表非弹性耗能衰减项;
将式(6)带入式(5),可得
| $I=k_1+k_2 \ln \left(\frac{E_0}{4 \pi}\right)-k_2 b \ln (\varDelta)-k_2 c \varDelta$ | (7) |
其中
| $E_0=\frac{\Delta \sigma M_0}{4 \mu}$ | (8) |
| $\ln M_0=d_1+d_2 M_{\mathrm{S}}$ | (9) |
式中,M0为地震矩,E0为能量。
将式(8)、式(9)代入式(7),可得
| $I=k_1+k_2 \ln \left(\frac{\varDelta \sigma \mathrm{e}^{d_1+d_2 M_{\mathrm{s}}}}{8 \mu \pi}\right)-k_2 b \ln (\varDelta)-k_2 c \varDelta$ | (10) |
将式(10)进行简化,并予以系数代换,可得到如下近似表达式
| $I=\gamma_1+\gamma_2 M_{\mathrm{S}}-\gamma_3 \ln (\varDelta)-\gamma_4 \varDelta$ | (11) |
| $I=\gamma_1+\gamma_2 M_{\mathrm{S}}-\gamma_3 \ln \left(\sqrt{a_2^2+H^2}\right)-\gamma_4 \sqrt{a_2^2+H_2}$ | (12) |
| $I=\gamma_1+\gamma_2 M_{\mathrm{S}}-\gamma_3 \ln \left(\sqrt{b^2+H^2}\right)-\gamma_4 \sqrt{b^2+H_2}$ | (13) |
以上各式中,I为烈度,a为长轴半径,b为短轴,H代表震源深度。
3.2.2 系数的确定应用最小二乘法进行统计回归,得到基于模型2的我国分区地震烈度衰减关系回归系数,见表 3。
| 表 3 模型2的系数拟合结果 Table 3 Coefficient fitting results of model 2 |
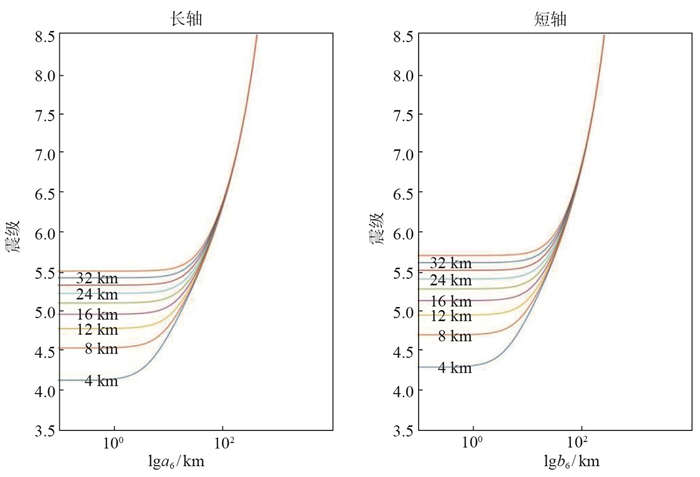
(1)我国东部地区地震震源深度对Ⅵ度(6度)区长短轴半径的影响。将表 3中我国东部地区模型1的拟合系数代入式(12)、(13),分析该区不同震中距地震的震源深度对Ⅵ度(6度)区长短轴半径的影响。烈度值为6度,以长、短半轴的对数为横坐标,震级为纵坐标,震源深度设为4 km≤H≤36 km,绘制在不同震源深度影响下震级与长短轴的关系图,结果见图 5(图中震源深度间隔4 km)。
|
图 5 基于模型2中我国东部地区地震震源深度对Ⅵ度(6度)区长短轴半径的影响 Fig.5 The influence of focal depth in the east of China on the radius of long and short axis in the area of Ⅵ degree (6 degree) in model 2 |
由图 5可见,震源深度参数对长轴的影响如下:H在4—36 km范围内,在近场范围内,R为0—10 km时,对应震级取值范围为4.1≤MS≤5.5,与模型1中长轴影响关系对比发现,震级相差约0.4;当R在10—100 km,在相同的震源深度和震级范围内,曲线斜率逐渐增大,衰减作用逐渐加快,直至中、远场范围,即R>100 km、MS>5.5时,各曲线逐渐汇合成为一条曲线。也就是说,对于长轴模型来说,当R在10—100 km、4.1≤MS≤5.5时,震源深度(4 km≤H≤36 km)参数对模型2的影响作用逐渐增大,直至H>36 km、MS>5.5、R>100 km时,震源深度参数对模型2长轴的影响基本消失。
震源深度参数对短轴的影响如下:H在4—36 km范围内,R为0—100 km时,对应震级取值范围为4.3≤MS≤5.7,与模型1中短轴影响关系相比,震级相差约0.3。当R在0—10 km,H在4—36 km范围内,对应震级取值范围为4.3≤MS≤5.7,震源深度参数对模型2短轴的影响基本不存在;当R在10—100 km,在相同的震源深度和震级范围内,曲线斜率逐渐增大,衰减作用逐渐加快,直至中、远场范围,即R>100 km、MS>5.7时,各曲线逐渐汇合成为一条曲线。也就是说,对于短轴模型来说,当R在10—100 km、4.3≤MS≤5.7时,震源深度(4 km≤H≤36 km)参数对模型2的影响作用逐渐增大,直至H>36 km、MS>5.7、R>100 km时,震源深度参数对模型2短轴的影响基本消失。
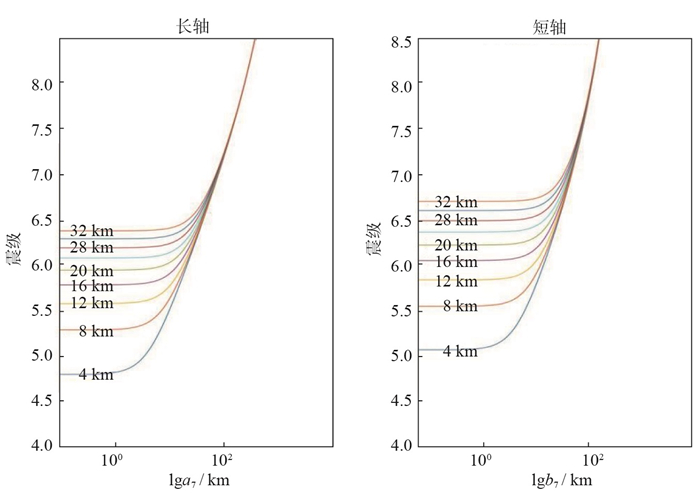
(2)我国西部地区地震震源深度对Ⅶ度(7度)区长短轴半径的影响。同理,基于模型2,绘制我国西部地区地震震源深度对Ⅶ度(7度)区长短轴半径的影响关系图,见图 6。由图 6可见,震源深度参数对长轴的影响如下:当R在0—100 km、H在4—36 km范围内,对应震级为4.7≤MS≤6.4,与模型1中长轴影响关系相比,震级相差约0.4。当R在0—10 km、H在4—36 km范围内,若4.7≤MS≤6.4,模型2的衰减作用几乎不存在;当R在10—100 km,在相同的震源深度和震级范围内,曲线斜率逐渐增大,衰减作用逐渐加快,直至中、远场范围,即R>100 km、MS>6.4时,各曲线逐渐汇合成为一条曲线。也就是说,对于长轴模型,当R在10—100 km、4.7≤MS≤6.4,震源深度参数对模型2的影响作用逐渐增大,直至H>36 km、MS>6.4、R>100 km时,震源深度参数对模型2的影响基本消失。
|
图 6 基于模型2中我国西部地区地震震源深度对Ⅶ度(7度)区长短轴半径的影响 Fig.6 The influence of focal depth on the long and short axis radius of Ⅶ degree (7 degrees) region in model 2 in Western China |
震源深度参数对短轴的影响如下:当R在0—100 km、H在4—36 km范围内,对应震级为5.0≤MS≤6.7,与模型1中短轴影响关系相比,震级相差约0.3。当R在0—10 km、H在4—36 km范围内,若5.0≤MS≤6.7,模型2的衰减作用几乎不存在;当R在10—100 km,在相同的震源深度和震级范围内,曲线斜率逐渐增大,衰减作用逐渐加快,直至中、远场范围,即R>100 km、MS>6.7时,各曲线逐渐汇合成为一条曲线。也就是说,对于短轴模型,当R在10—100 km、5.0≤MS≤6.7范围内,震源深度参数对该模型的影响作用逐渐增大,直至H>36 km、MS>6.7、R>100 km时,震源深度参数对模型2短轴的影响基本消失。
4 历史震例验证选取我国东、西部地区2008年以来烈度值I≥Ⅵ的MS≥5.0地震事件,分别计算模型1、2和椭圆烈度衰减关系模型下的地震烈度值,与实际烈度值进行关系拟合,验证3种模型的可信度。
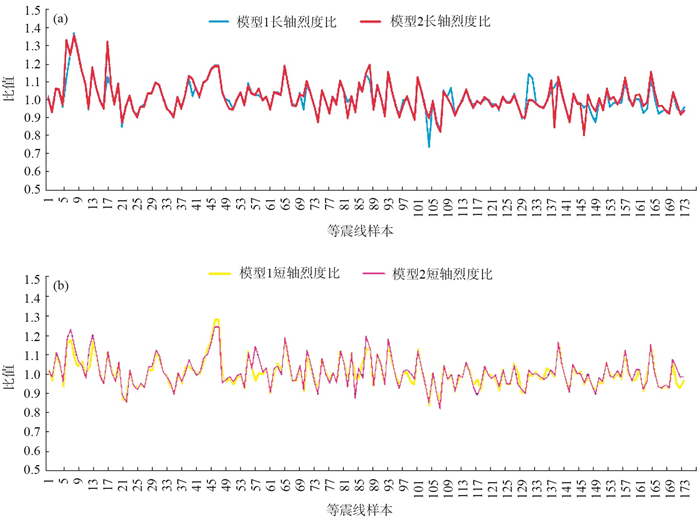
4.1 地震等震线长、短轴半径对比基于所选震例,根据模型1、2的分区结果,依次带入实际地震参数值,分别得出相应烈度值,并以实际烈度值与模型烈度值之比为指标,检验经验统计模型与实际烈度评定结果的吻合程度(由于地震烈度衰减关系具有明显的地域性特征,故在选取震中位置对应区域的衰减烈度公式时,以我国东部和西部地区所划分的小区域为准,即西南地区、西北地区、东北—华北地区、华中—华南地区),结果见图 7。
|
图 7 所选震例的实际烈度与基于2种模型计算所得烈度的比值关系 (a)长轴;(b)短轴 Fig.7 The ratio of the actual intensity of the selected earthquake cases to the intensity calculated based on the two models |
(1)真实烈度值与长轴烈度衰减关系模型结果对比:真实烈度值与基于模型1长轴烈度衰减关系模型计算的烈度值比值最大值为1.762 2,最小值为0.736 5,中位数为1.003 3,平均值为1.017 8;真实烈度值与基于模型2长轴烈度衰减关系模型计算的烈度值比值最大值为1.451 1,最小值为0.802 4,中位数为1.004 1,平均值为1.015 9。
(2)真实烈度值与短轴烈度衰减关系模型结果对比:真实烈度值与基于模型1短轴烈度衰减关系模型计算的烈度值比值最大值为1.957 2,最小值为0.842 2,中位数为1.000 8,平均值为1.013 8;真实烈度值与基于模型2短轴烈度衰减关系模型计算的烈度比值最大值为1.499 5,最小值为0.822 6,中位数为1.004 9,平均值为1.016 6。
所选震例的实际烈度与基于2种模型计算所得烈度的比值关系见图 7。由图 7可见,基于模型1、2所得烈度值与实际地震烈度变化趋势基本一致,说明通过2种模型拟合得到的地震烈度衰减关系用来评定地震烈度值时有一定规律可循,且与地震实际烈度值稍有偏差,偏差范围在0.90—1.05倍。
4.2 与椭圆烈度衰减关系对比 4.2.1 椭圆衰减关系模型地震烈度衰减公式取自目前我国常用椭圆烈度衰减关系模型(陈达生等,1989):
| $I=A+B M+C \ln \left(R+R_0\right)+\varepsilon$ | (14) |
式中,I为地震烈度;R表示长、短轴半径;M为地震震级;R0为近场饱和因子;参数A、B、C为回归常数;ε为回归分析中表示不确定的随机变量,通常假定为正态分布,其均值为零。
4.2.2 回归系数结果应用上述同一组数组,采用最小二乘法进行统计回归,得到基于椭圆烈度衰减关系模型的我国分区地震烈度衰减关系回归系数,见表 4。
| 表 4 基于椭圆烈度衰减关系模型的我国分区地震烈度衰减关系回归系数 Table 4 Table of regression coefficient of seismic intensity attenuation coefficient in China |
基于所选震例,将表 4中数据代入椭圆烈度衰减关系模型,计算得到该模型烈度值,以实际烈度值与该烈度值之比为指标,验证经验统计模型与实际烈度评定结果的吻合程度。
实际烈度值与基于椭圆烈度衰减关系模型计算所得烈度值之比为:①长轴:二者比值最大值为1.344,最小值为0.772,中位数为1.028,平均值为1.032;②短轴:二者比值最大值为1.261,最小值为0.836,中位数为1.029,平均值为1.029。
4.3 3种模型结果对比将模型1、2和椭圆烈度衰减关系模型(长、短轴)烈度比值结果进行对比,结果见图 8。将椭圆模型与模型1的长、短轴烈度比结果进行对比,可知椭圆模型长轴烈度比值最大值较小(偏差为0.40),最小值偏大(偏差为0.04),平均值偏大(偏差为0.03);其短轴烈度比值最大值偏小(偏差为0.20),最小值偏大(偏差为0.01),平均值偏大(偏差为0.1)。将椭圆模型与模型2的长、短轴烈度比结果进行对比,可知椭圆模型长轴烈度比值最大值偏小(偏差为0.11),最小值偏小(偏差为0.10),平均值偏大(偏差为0.01);其短轴烈度比值最大值偏小(偏差为0.20),最小值偏大(偏差为0.01),平均值偏大(偏差为0.01)。

|
图 8 3种烈度衰减关系模型与实际烈度比值关系对比 (a)长轴;(b)短轴 Fig.8 Comparison of ratios of three intensity attenuation models with actual intensity |
对比可知,与模型1、2相比,基于椭圆烈度衰减关系计算所得烈度与实际烈度比值的平均误差均偏大。也就是说,基于模型1、2计算所得烈度值更接近真实地震烈度,表明通过震源深度参数进行约束,烈度计算结果精度更高。
基于3种烈度衰减关系模型计算烈度,所得数值与真实地震烈度存在偏差,这可能是因为,实际烈度衰减关系受震源特性、深部构造、传播介质、场地条件、建筑物结构类型和居民点分布、地形等因素的影响(汪素云等,2000)。
5 结论与讨论收集1970年以来我国418次MS≥4.0地震的烈度等震线和震源深度相关资料,基于2种考虑震源深度的烈度衰减关系模型,采用最小二乘法拟合我国东、西部地区及其分区(西南、西北地区,东北、华北和华中、华南地区)的地震烈度衰减关系,探讨2种模型下,震源深度在4 km≤H≤36 km时,我国东部地区震源深度对Ⅵ度(6度)区长短轴半径的影响和我国西部地区震源深度对Ⅶ度(7度)区长短轴半径的影响,分析发现:在同一震源深度下,模型1、2对应的震级范围有所不同。
对于模型1下Ⅵ度(6度)区长轴:当R在10—100 km、4.5≤MS≤5.5时,震源深度参数(4 km≤H≤36 km)对模型1长轴的影响作用逐渐增大,直至H>36 km、MS>5.5、R>100 km时,震源深度参数对模型1长轴的判定影响基本消失;对于模型1下Ⅵ度(6度)区短轴:当R在10—100 km、4.6≤MS≤5.8,震源深度参数对模型1的影响作用逐渐增大,直至H>36 km、MS>5.8、R>100 km时,震源深度参数对模型1短轴的影响基本消失;对于模型2下Ⅵ度(6度)区长轴、短轴,在震中距和震源深度相同情况下,与模型1相比,仅震级参数相差0.3—0.4。
对于模型1下Ⅶ度(7度)区长轴:当R在10—100 km、5.2≤MS≤6.4时,震源深度(4 km≤H≤36 km)参数对模型1的影响作用逐渐增大,直至H>36 km、MS>6.4、R>100 km时,震源深度参数对模型1长轴的影响基本消失;对于模型1下Ⅶ度(7度)区短轴:当R在10—100 km、5.2≤MS≤6.4时,震源深度(4 km≤H≤36 km)参数对模型1的影响作用逐渐增大,直至H>36 km、MS>6.7、R>100 km时,震源深度参数对模型1短轴的影响基本消失;对于模型2下Ⅶ度(7度)区长轴、短轴,在震中距和震源深度相同情况下,与模型1相比,仅震级参数相差0.3—0.4。
选取2008年以来我国东、西部地区发生的MS≥5.0地震事件,以实际烈度值与模型(模型1、2及椭圆烈度衰减关系模型)烈度值之比为指标,验证3种模型与实际烈度评定结果的吻合程度,结果表明:模型1、2所得烈度与实际烈度的比值变化趋势基本一致,表明2个模型所得烈度预测值与实际值趋于一致;与模型1、2相比,基于椭圆烈度衰减关系模型所得比值的平均值稍大,表明2种考虑震源深度的烈度衰减关系模型在计算地震烈度时精度更高。但是,受震源特性、深部构造、传播介质、场地条件、建筑物结构类型和居民点分布、地形等因素影响,3种模型结果与实际烈度仍存在偏差。
综上所述,2种考虑震源深度的烈度衰减关系模型,在我国东、西部地区适用范围如下:西部地区:4.0≤MS≤8.6,0≤R≤486 km,3 km≤H≤74 km;东部地区:4.0≤MS≤8.0,0≤R≤476 km,4 km≤H≤36 km。
常银辉. 基于断层距的地震烈度衰减关系研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2012.
|
陈达生, 刘汉兴. 地震烈度椭圆衰减关系[J]. 华北地震科学, 1989, 7(3): 31-42. |
崔鑫. 华南地区地震烈度衰减模型的建立[J]. 华南地震, 2010, 30(2): 61-66. |
金星, 张红才, 李军, 等. 地震仪器烈度标准初步研究[J]. 地球物理学进展, 2013, 28(5): 2336-2351. |
卢建旗, 李山有, 李伟, 等. 基于地震等震线面积和长轴半径的烈度衰减关系[J]. 地震工程与工程振动, 2013, 33(2): 16-26. |
孟宪东, 龚平, 金赤兵. 用烈度衰减的椭圆模型标度华北地区历史地震震级[J]. 东北地震研究, 1987(3): 27-35. |
聂高众, 徐敬海. 基于震源深度的极震区烈度评估模型[J]. 地震地质, 2018, 40(3): 611-621. |
沈大开, 高德潜. 改进的断层破裂烈度衰减模型[J]. 地震工程与工程震动, 1987, 7(2): 69-77. |
王继, 俞言祥. 华中、华南中强地震区地震烈度衰减关系研究[J]. 震灾防御技术, 2008, 3(1): 20-26. |
汪素云, 俞言祥, 高阿甲, 等. 中国分区地震动衰减关系的确定[J]. 中国地震, 2000, 16(2): 99-106. |
汪素云, 裴顺平, Hearn M, 等. 利用ML幅研究地壳横波Q值Ⅱ: Q横向变化特征[J]. 地球物理学报, 2008, 51(1): 133-139. |
汪素云, 裴顺平, 许忠淮, 等. 利用ML振幅研究地壳横波Q0值Ⅰ: 不同构造区的衰减特征[J]. 地球物理学报, 2007, 50(6): 1740-1747. |
王小龙, 吴晓莉. 重庆及邻近地区地震烈度衰减关系分析与确定[J]. 四川地震, 2004(2): 8-11. |
王晓军, 文毅, 鲁权, 等. 陕西分区烈度衰减关系研究[J]. 灾害学, 2012, 27(4): 98-102. |
郁曙君. 确定烈度衰减关系的椭圆投影两步拟合法[J]. 地震学报, 1993, 15(1): 109-114. |
张方浩, 蒋飞蕊, 李永强, 等. 云南地区地震烈度评估模型研究[J]. 中国地震, 2016, 32(3): 511-521. |
张苏平, 陈文凯, 周中红, 等. 中国西部地区大地震(MS≥7)烈度衰减关系改进[J]. 自然灾害学报, 2015, 24(1): 104-113. |
郑广芬, 陶夏新. 用人工神经元网络方法建立地震烈度衰减关系[J]. 地震工程与工程振动, 1993, 13(1): 60-66. |
郑韵. 震源机制和余震序列在地震应急烈度快速判定中的应用研究[D]. 北京: 中国地震局地震预测研究所, 2015.
|
中国地震局监测预报司. 中国大陆地震灾害损失评估汇编: 1996-2000[M]. 北京: 地震出版社, 2001.
|
中国地震局震害防御司. 中国近代地震目录(公元1912年-1990年)[M]. 北京: 中国科学技术出版社, 1999.
|
中国地震局震灾应急救援司. 2001-2005年中国大陆地震灾害损失评估汇编[M]. 北京: 地震出版社, 2010.
|
周锡元, 苏经宇, 王广军. 以断层破裂震源模式为基础的烈度衰减规律[J]. 地震学报, 1987, 9(4): 417-426. |
 2023, Vol. 44
2023, Vol. 44


