野外布设台阵越来越多，不仅可以记录到地震信号，也能记录到丰富的连续噪声信息，这些信息来自地球震动、固体潮汐、大气气压变化、海浪拍击海岸等。起初这些连续的背景噪声记录被视为无用的干扰信号，在进行天然地震研究时，通过各种方法手段去除噪声而凸显地震信号，后来经过科学家地不断研究，发现背景噪声记录也能用于地下速度结构研究（Duvall et al，1993），且具有较高的分辨率。

早在1957年，Aki（1957）就通过布设合理的台站，使用背景噪声记录获取了浅层地壳中面波频散信息，提出可以采用空间自相关方法研究地表浅层介质；1968年，Claerbout（1968）提出台站间的反射响应，通过在三维各向异性介质中2个台站的投射波场计算得到互相关函数，该思路在太阳地震学中得到成功应用。发展到1993年，Duvall等（1993）通过互相关计算太阳表面的噪声场，提出声波时距曲线，并得到太阳外层的三维流速度结构，这一研究成果奠定了背景噪声技术发展的里程碑，越来越多的研究和学术领域，包括超声波、水底声波场，均发现从两点间的噪声信号提取的互相关函数与格林函数的相似度较高。2001年，Lobkis等（2001）在声学研究领域，对测量得到的热起伏噪声进行互相关计算，得到两点间的格林函数，这一开创性的研究成果被运用到地震学中。基于之前的理论指导，一种新的地震学方法诞生并逐渐发展起来，这种方法已证实可用于研究壳幔速度结构，即背景噪声层析成像。2003年，Campillo等（2003）发现，在地震尾波记录中也能提取格林面波函数；2004年，Shapiro等（2004）通过台站对地震噪声垂向分量信息进行互相关计算，得到地球结构信息。2005年，Shapiro等（2005）用此方法得到美国南加州周期为7.5 s和15 s的瑞利面波群速度分布图。之后地震背景噪声成像方法得到飞速发展，应用范围小到地方、大到全球尺度，研究内容包括了瑞利面波相速度和群速度、勒夫面波群速度和相速度，研究周期可以是几秒或者上百秒，对应深度从地球近地表到地壳浅层到整个地壳以及上地幔（Shapiro et al，2005；Yao et al，2006；房立华等，2009；Fang et al，2010, 2015；郑定昌等，2014；Li et al，2016）。研究人员证实，层析成像结果与已知地质构造吻合较好，表明背景噪声成像方法是有效的（姚华建等，2004）。本文在此基础上，对其在地震学中采用的方法理论原理、应用效果和未来发展前景进行综述和展望。

利用两点间记录的连续背景噪声信号进行互相关函数计算，可以得到两点间的格林函数（Weaver et al，2005）。格林函数在地震学中的物理意义是：把源当做一个接收点产生的记录，在另一接收点记录到的脉冲响应就是2个接收点之间的格林函数，此脉冲响应可以认为是由无限多个具有不同周期的连续正弦波列组成，始于震源事件发生，终止于尾波结束，包含2个接收点间地震波传播的全部信息，反映出地下介质结构的信息，互相关函数的导数就是经验格林函数（图 1），经验格林函数不是真实的格林函数，是真实格林函数中的面波部分。同时，在理论方面，促使不同领域的研究者来证实其基于不同物理模型的假设，相关假设有：模式均分假设（Weaver，2005）、时间反对称理论（Derode et al，2001, 2003）、稳相近似理论（Snieder，2004）、互相关类型的表示定理（Wapenaar et al，2004），对互相关函数和经验格林函数的关系给出不同理论解释，以证实二者具有内在一致性。

图 1(Fig.1)

图 1 用背景噪声计算互相关函数提取格林函数示意图（引自Yao et al，2006） 黑色箭头代表散射波场，是震源产生的记录经过多次散射形成的，其中噪声信号先后被2个台站接收，震相不发生变化，通过对2个台站进行互相关计算，得到两接收点之间的格林函数 Fig.1 Schematic diagram of extracting Green's function by calculating cross-correlation function of background noise (From Yao et al, 2006)

面波具有频散特性，可从经验格林函数中提取相速度或群速度频散曲线，地震学家通常采用单台法或双台法来提取面波频散特性（Brune et al，1960）。20世纪60年代初，Alexander等（1963）把数值滤波技术用于面波频散测量；Pliant等（1964）首次提出时变滤波法（TVF）来测量相速度，并得到双台相速度频散，此项技术应用奠定了面波频散测量发展的基础。到1969年，Landisman等（1969）提出移动窗分析法；紧接着，Dziewonski等（1969）提出多重滤波法；Herrin等（1977）为了使提取的相速度或群速度频散曲线更加精确和稳定，提出相位匹配滤波法。

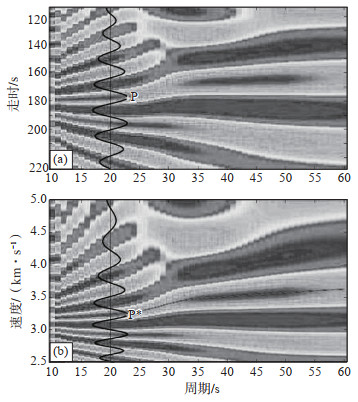
基于时变滤波思想（徐果明等，2000），姚华建等（2004）提出基于图像分析的相速度频散曲线快速提取方法，是一种基于双台法提取面波频散特性的有效方法，其原理是：对2个台站的连续波形记录做零漂校正、去仪器响应，归一化处理后采用多重滤波法，得到双台间不同周期T的波对应的不同到时，对归一化双台记录做加可变宽移动时窗的窄带滤波处理，得到频率上基本同频的简谐波（姚华建等，2004）。与传统双台法等值线手工描点勾画方法相比，该方法只需在频散曲线附近点动鼠标，便可快速追踪到整条频散曲线，提高了面波频散特性提取精度和效率，不仅可以清晰展现频散特征，而且可以有效识别和分析频散曲线（图 2）。人机交互为处理大批量背景噪声数据资料提供了快速可靠的软件基础。

图 2(Fig.2)

图 2 相速度频散曲线测量示意（引自Yao et al，2006） (a)对每一周期的双台窄带滤波结果做互相关，求取面波经验格林函数的振幅矩阵图像，黑色波形为归一化处理的经验格林函数，中心周期20 s；(b)反映周期和相速度关系的振幅矩阵图像，P处黑色实线为相速度频散曲线测量图 Fig.2 Schematic of phase velocity dispersion curve measurement (From Yao et al, 2006)

以往面波成像一般都假设面波沿大圆路径传播，路径是固定的，不随频率变化，也不随结构变化。但是做体波层析成像时，由于结构差异比较大，研究人员必须考虑体波传播路径的射线追踪。在全球地震学中，面波反演时由于群速度或相速度变化都在7%以内，这时面波沿大圆路径传播与所考虑面波走的实际路径接近，对反演结果几乎没什么影响，便不考虑面波射线路径的弯曲。但据前人研究结果（Huang et al，2010；李想等，2015）表明，当地下介质速度结构变化较大，且某一周期的面波相速度相对于平均相速度的异常大于10%时，面波会偏离大圆路径传播，导致反演结果与假设面波沿大圆路径反演的结果出现偏差。

使用面波频散测量数据进行层析成像或背景噪声层析成像通常采取两步法：①基于射线追踪理论或二维有限频敏感核使用走时层析成像方法反演得到二维相速度或群速度分布图（Yao et al，2006）；②在每个网格节点逐点反演面波频散数据，作为剪切波速度随深度的函数的一维剖面，然后用一维模型反演出三维模型（Yao et al，2008）。Fang等（2015）提出基于射线追踪的面波频散直接反演方法，把所有双台路径频散曲线各个不同周期的走时信息合在一起，直接反演出三维剪切波速度结构，这种方法省去了传统两步法（Ritzwoller et al，2002；Yao et al，2006）中通过由频散曲线做走时成像得到2D相速度/群速度分布图这一步，并考虑了复杂介质中面波会偏离大圆路径传播，受到地下结构的控制，不同频率的面波走得路径不一样，用快速行进法（Rawlinson et al，2004）进行面波传播路径的射线追踪。

理论研究表明，背景噪声源分布的均匀性对互相关函数和经验格林函数的近似程度十分重要。由于地球内部结构的不均匀性，实际观测到的噪声分布并不均匀，所以通过合理布设台阵、改进数据处理方法、分析背景噪声特征等方法，可以进一步完善噪声源的均匀分布，进而提高反演结果的分辨率。

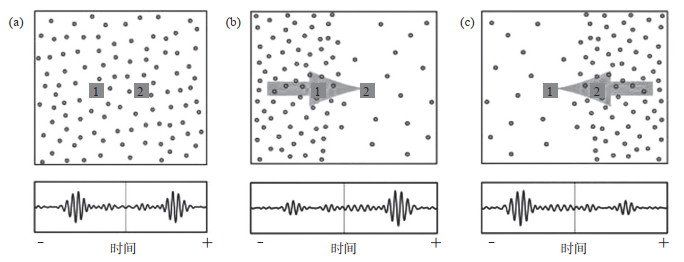
任意2个台站间计算的互相关函数，其振幅取决于2个台站连线方向的能量流（Paul et al，2005），如果台站两侧的噪声源分布均匀，说明2个方向的能量流是相同的，则互相关函数的振幅和到时大小是完全相同的；如果台站两侧的噪声源分布不均匀，则会发现互相关函数的到时相同、振幅不对称，说明互相关函数正负分支能量流的来源方位不同（图 3）。同时，互相关函数2个方向的能量流在分布时间上表现为一定的季节性变化特征，会影响频散曲线提取的稳定性。因此，有必要分析背景噪声源的分布特征和季节性变化特征。Stehly等（2006）选取了美国东部、欧洲西部、加利福尼亚地震台网记录的垂直分量背景噪声数据，通过分析互相关函数因果信号和非因果信号的不对称性，发现不同频带的噪声起源是不同的：环境背景噪声在5—10 s和10—20 s周期之间存在2个明显的峰值，10—20 s周期之间存在的峰值称为第一类地脉动，会随季节的变化而变化；5—10 s周期之间存在的峰值称为第二类地脉动，不随季节变化。

图 3(Fig.3)

图 3 噪声源分布对所得互相关函数的影响（引自Stehly et al，2006） (a)当1、2两侧的噪声源分布均匀时，得到的互相关函数是对称的；(b-c)当1、2两侧的噪声源分布不均匀时，得到的互相关函数是不对称的（引自Stehly et al，2006） Fig.3 The influence of noise source distribution on the resulting

2004年，Shapiro等（2004）通过台站对地震噪声垂向分量信息进行互相关计算，得到地球结构信息。2005年，Shapiro等（2005）用此方法得到美国南加州周期为7.5 s和15 s的瑞利面波群速度分布图。自此，背景噪声成像方法得到飞速发展。Yang等（2009）利用连续的背景噪声记录反演了青藏高原东北缘的速度结构，结果表明柴达木盆地下地壳有高速异常，而中上地壳存在低速异常。Li等（2009）通过四川地震台网记录的噪声数据，获得周期为8—44 s川西及藏东地区Rayleigh波群速度分布，计算并绘制研究区10 km、25 km、45 km深度S波速度分布图像。Zheng等（2010）利用布设在青藏高原东北部、四川盆地和鄂尔多斯地块台阵的160个台站记录的背景噪声数据，通过噪声层析成像，反演出不同周期的瑞利面波相速度图像。Li等（2012）利用青藏高原东北缘地区156个台站的三分量连续背景噪声记录，得到所有可能台站对的面波互相关函数和瑞利波群速度频散曲线以及勒夫波群速度频散曲线，联合反演得到周期为7—50 s瑞利波群速度和勒夫波群速度分布图像，揭示了青藏高原北部低速层主要存在于中下地壳。Lin等（2013b）利用布设在美国加利福尼亚的密集台阵，获得0.5—4 Hz频段的相速度分布。郑现等（2012）利用背景噪声提取的瑞利面波，反演得到中国东部地区的地壳群速度结构。Tang等（2013）基于噪声记录，采用远震双重面波层析成像法，得到华北克拉通三维地壳和上地幔S波速度结构，结果显示，华北盆地与鄂尔多斯地块具有不同的化学性质。范文渊等（2015）利用北京大学宽频带流动观测台阵记录的连续背景噪声记录，反演获得观测台阵下方周期为6—60 s的瑞利波相速度图像，进一步反演获得了青藏高原东部和周边地区地壳三维剪切波速度结构，结果表明，地幔岩浆的底侵作用可能是引起该地区地壳增厚的主要机制。叶庆东等（2015）使用背景噪声数据资料，得到大别、苏鲁地区的地壳上地幔结构。郭瑛霞等（2017）利用祁连山地区固定台的垂直分量连续背景噪声记录，采用基于射线追踪的面波频散直接反演方法，得到祁连山地震带下方5—40 km深度范围内S波速度分布图像（图 4），研究结果与前人具有一致性。冯红武等（2019）利用陕西及邻区257个宽频带台站记录的背景噪声数据，采用基于射线追踪的面波频散直接反演方法，获得了渭河盆地及邻区地壳上地幔顶部S波速度结构，结果表明，秦岭造山带存在青藏高原物质E流的下地壳流通道的可能性不大。孟亚锋等（2019）利用瑞利面波相速度，反演得到郯庐断裂带中南段及邻区地壳速度结构与变形特征，结果显示，研究区域内中地壳存在多处横波高速异常体。顾勤平等（2020）利用瑞利面波得到郯庐断裂带中南段及邻区的群速度结构，图像揭示了郯庐断裂带中南段及邻区地壳上地幔速度结构具有横向分块和纵向成层的非均匀性特征。李玲利等（2020）利用噪声成像法，对合肥市区城市下方的地壳浅层速度结构进行成像，揭示了合肥市下方地壳浅部的横向不均匀性和纵向成层性。曾求等（2020）计算得到四川威远地区5km范围内三维剪切波速度模型。付媛媛等（2020）基于青藏高原东北缘的流动密集地震台阵，采用背景噪声成像方法，获得瑞利波和勒夫波二维相速度分布。黄翔等（2021）基于中国地震科学台阵探测项目在华北中部布设的306个台站记录的波形数据，利用背景噪声层析成像方法开展了瑞利波相速度和方位各向异性研究。朱子杰等（2021）通过收集密集地震台阵观测资料，利用环境噪声提取瑞利面波频散曲线，采用多角度频散曲线反演方法，获得青藏高原东南缘地壳和上地幔顶部高分辨率的地震S波速度和各向异性图像。孔祥艳等（2021）利用新疆地震台网固定台站和流动台数据，采用背景噪声层析成像方法，获得天山及邻区周期为10—50 s的瑞利面波相速度分布图像，并反演得到研究区地壳上地幔S波速度结构，研究结果表明，准噶尔盆地沉积盖层南深北浅，在天山造山带北部和南部的盆山交界附近，地壳内部存在明显的向造山带方向倾斜的低速区。张丽娜等（2018）利用福建及邻区108个宽频带地震台波形记录，计算得到研究区1—20 s周期的瑞利波和勒夫波群速度频散数据，揭示了福州盆地和漳州盆地在浅层结构中的低速异常。

图 4(Fig.4)

图 4 祁连山地区不同深度的剪切波速度分布（郭瑛霞等，2017） (a) 深度为5 km；(b) 深度为18 km；(c) 深度为30 km；(d) 深度为40 km Fig.4 Shear wave velocity maps at different depths

除了广泛应用于地下速度结构的研究外，也有学者将背景噪声成像方法用来预测煤矿的瓦斯分布（黄宇奇等，2021），这是一种全新的技术形式。还有学者使用国产分布式光纤声波传感器，利用480 m埋地光缆记录背景噪声，计算得到噪声互相关函数，获得高频瑞利面波信号，提取相速度频散曲线，证明结果与传统检波器记录和主动源结果较一致（林融冰等，2020）。

背景噪声成像的发展集中于提高成像分辨率。随着研究深度的增加，面波成像分辨率逐渐降低，深部结构细节的可信度会降低，为压制背景噪声成像方法中的反演假象，提高反演分辨率，利用噪声面波频散和接收函数联合反演方法获取地下介质速度结构，也被应用到诸多研究中（王未来等，2009；郑现等，2015；郑晨等，2018；高业欣等，2020）。

背景噪声层析成像方法不依赖于天然地震，可以显著提高地下速度结构成像的空间分辨率。随着日益增多的密集固定地震台阵和流动地震台阵的布设，该方法得到广泛应用，如通过体波、面波速度结构成像，监测地下介质波速变化，预测煤矿瓦斯分布。然而，该方法仍存在一些问题需要进一步解决和完善，如：如何从地震仪观测的三分量连续背景噪声记录中提取高阶频散的信息进行成像，数据处理方法有待更深入研究；如何在提高结果精度的同时，提高频散曲线测量自动化处理的速度，也是噪声成像过程中必要考虑的问题之一；如何利用背景噪声方法实现地下结构的时间变化和空间变化的有机结合，将大震前后的波速变化达到实际应用的程度，需要更多科研工作者的辛勤努力。

背景噪声成像方法从杂乱无章的信号中提取有用的地下介质信息，已成为研究地壳速度结构的一种重要方法。未来随着研究思路、更多密集地震台站的布设和方法的进一步完善，在更高质量数据的支持下，这项工作将具有深远而重大的意义。在深化现有研究的同时，应用于更多新的研究领域，为深刻认识地球内部结构提供更多值得关注的成果。