0 引言

测震台站是地震监测预警的基本单元，是获取地表运动观测数据的重要节点。具备无失真地、完整地观测、记录地震波的能力是测震台站的首要目标，这一目标的实现主要取决于测震台站技术系统的性能和测震台站观测环境（中国地震局监测预报司，2017）。观测场地环境噪声水平是影响观测数据质量的主要因素之一，高频段观测数据主要受工业生产、人类活动、交通运输等的影响，微震频段观测数据主要受海洋活动的影响，而温度、气流变化等主要影响低频段观测数据（吴建平等，2012；杨千里等，2019；蔡辉腾等，2019；安全等, 2021, 2021）。为减少自然条件、人类活动等对观测数据的干扰，国内研究者探索了降低环境噪声水平的方法，以提高观测数据质量。唐杰等（2020）、许自龙等（2021）分别应用、小波阈值等去噪法的高频背景噪声压制方法开展相关研究，得到较好结果。

本文对二连浩特地震台井下连续观测数据中的干扰数据进行小波分析并计算观测数据加速度PSD值和相应的PDF值，分析地震环境噪声水平干扰特征，寻找并排查干扰源，以降低外界噪声的影响，提高观测数据质量。

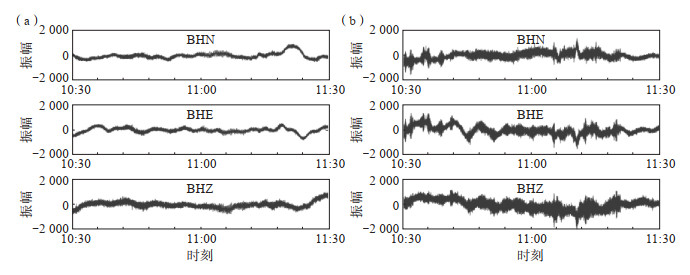
1 台站信息

二连浩特市地处内蒙古高原中部阴山山脉以北的层状高平原区，海拔910—1 000 m。除零星洼地外，地势平坦。处于阴山—燕山地震带北部，蒙古弧形构造带与查干诺尔西拉沐伦断裂的交汇部位。二连浩特测震台站为井下观测方式，配有甚宽频带地震计和24位数据采集器，仪器信息见表 1。2022年8月10日二连浩特地震台观测数据出现异常，对比8月9日10:30—11:30与10日10:30—11:30的波形可以发现，异常主要表现为三分量噪声变大（图 1）。

2 原理

把长度为1 h的数据段（采样率100/s）分为42个记录段，为了降低PSD方差，相邻记录段间重叠50%，每个记录段长度约为160 s。为降低长周期对功率谱估计的偏差，每个记录段进行去长周期、去均值预处理；对预处理后的记录段数据进行快速傅里叶变换，得到以频率为自变量的速度PSD值，再把速度PSD值转换至加速度PSD值；最后进行平滑处理和PSD值PDF分布计算。对噪声功率谱进行计算后可以得到异常干扰频段，对其进行小波变换，并进行滤波，恢复异常波形正常形态。

2.1 计算功率谱密度

对周期时间序列的有限范围傅里叶变换可表示为

$ Y\left(f, T_r\right)=\int_0^{T_r} y(t) \cdot \mathrm{e}^{-i 2 \pi f t} \mathrm{~d} t $

(1)

式中，T_r为时间序列段长度；f为频率。

对于离散频率，其傅里叶变换为

$ Y_k=\frac{Y\left(f_k, T_r\right)}{\Delta t} $

(2)

式中，f_k= k/(N∆t)，其中，k=1，2，3，⋯，N-1；Δt为采样间隔（0.01 s）；N= T_r/∆t，为截取时间段的采样点数。

功率谱密度PSD为

$ \operatorname{PSD}_k(f)=\frac{2 \Delta t}{N}\left|Y_k\right|^2 $

(3)

采用下式将速度PSD值转换为加速度PSD

$ \operatorname{PSD}_{a, k}(f)=(2 \pi f)^2 \operatorname{PSD}_k(f) $

(4)

为反映真实地动噪声值，需用下式扣除仪器传递函数的影响

$ \operatorname{PSD}_a(f)=\frac{P_{a. \mathrm{k}}(f)}{|H(f)|^2} $

(5)

式中，PSD_ɑ(f)为真实地表运动加速度功率谱。

2.2 平滑处理

为了使PSD在频域对数坐标中呈等间隔采样，采用1/3倍频均值平滑

$ \operatorname{PSD}_a\left(f_{\mathrm{c}}\right)=\frac{1}{n} \sum\nolimits_{f_{\mathtt{ι}}}^{f_{\mathrm{h}}} \operatorname{PSD}_a\left(f_{\mathrm{c}}\right) $

(6)

式中，f_ι = 2^-1/6f_c，为低频拐角频率；f_h = 2^1/6f_c，为高频拐角频率；n为介于二者之间频率的个数。由式（6）得到中心频率f_c的PSD_ɑ(f)平均值PSD_ɑ(f_c)，将其作为f_c的加速度功率谱密度的PSD值，中心频率f_c以1/9倍频程为增加步长，即下一个中心频率f_c = 21/9 f_c，重新计算相应的f_ι、f_h，然后将新的f_ι与f_h之间的PSD平均值作为下一个中心频率f_c的PSD取值。如此，在f_c的取值范围0.01—50.00 Hz内，每个记录段的PSD值随频率变化情况可由在对数坐标系中呈等间隔采样的中心频率的PSD值来表示。

2.3 计算概率密度函数

每个中心频率f_c的PSD概率密度函数为

$ P_{\mathrm{PSD}}\left(f_{\mathrm{c}}\right)=N_{\mathrm{P}f_{\mathrm{c}}} / \mathrm{N}_{f_{\mathrm{c}}} $

(7)

其中，N_Pfc为f_c的频点的记录段总数；N_Pfc为f_c的频点的PSD值落在某PSD取值范围内的记录段个数。

2.4 小波变换

设ψ(t)∈L²(R)，L²(R)表示平方可积的实数空间，即能量有限的信号空间，其傅里叶变换为ψ(ω)。当ψ(ω)满足下列允许条件时

$ F(\omega)=\int_{-\infty}^{+\infty} \frac{|\psi(\omega)|^2}{\omega} \mathrm{d} \omega <+\infty $

(8)

称ψ(t)为一个小波母函数（基本小波）。将小波母函数ψ(t)进行伸缩和平移，则有

$ \mathrm{WT}(a, \tau)=\frac{1}{\sqrt{a}} \psi\left(\frac{t-\tau}{a}\right) \mathrm{d} t $

(9)

称WT(a, τ)为连续小波基函数，其中，a为尺度因子；τ为平移因子。

对于任意的函数f(t)∈L² (R)的连续小波变换为

$ \mathrm{WT}(a, t)=\frac{1}{\sqrt{a}} \int_{-\infty}^{+\infty} f(t) * \psi\left(\frac{t-\tau}{a}\right) \mathrm{d} t $

(10)

其重构公式为

$ f(t)=\frac{1}{C_\psi} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} \frac{1}{a^2} \mathrm{WT}_f(a, \tau) \psi\left(\frac{t-\tau}{a}\right) \mathrm{d} a \mathrm{d} \tau $

(11)

3 异常分析 3.1 傅里叶变换分析

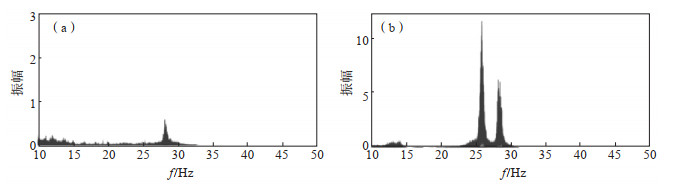
选取二连浩特地震台井下观测波形变幅较明显的2022年8月9日10:30—11:30与10日10:30—11:30两个时段观测数据进行傅里叶变换，发现8月10日数据中含有较大的集中在25—30 Hz的高频干扰信号（图 2）。

3.2 PSD分析

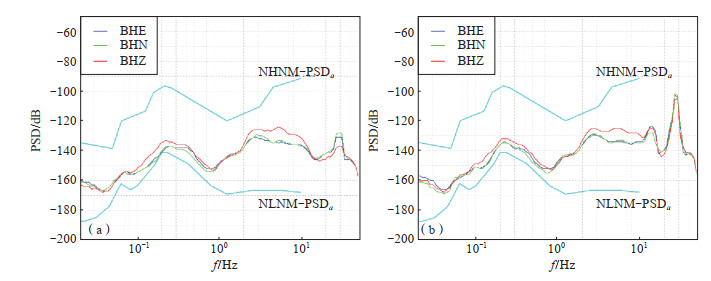
进一步对连续观测波形数据进行分析，分别计算了2日PDF最大值所对应的PSD平均值（图 3），以研究环境噪声干扰特征。

由图 3可见，在低于10 Hz频段，无干扰数据与有干扰数据的三分量PSD值基本一致，说明在10 Hz以下的频段，干扰对观测数据几乎没有影响。在10 Hz以上的高频段，8月10日PSD数据曲线出现明显异常变化，而高频段观测数据主要受工业生产、人类活动、交通运输等的影响，综合考虑观测场地周围环境与受干扰时段的时间特征可以推断，观测场地附近施工产生干扰的可能性较大。现场调查后发现，观测场地附近存在私自采矿的情况，观测数据受干扰时段与生产时间高度一致。经协商阻止采矿后，观测数据恢复正常。

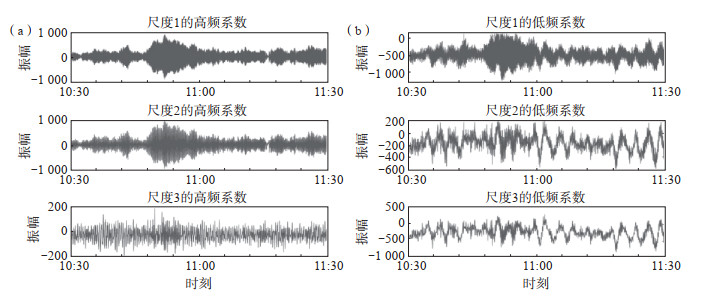
4 干扰数据的处理

小波变换具有较强的数据相关性，它不仅能使信号能量在小波域集中到一些大的有限的系数中，而且可使噪声的能量分布于整个小波域。因此经小波分解后，信号的小波变换系数大于噪声的小波变换系数，故可认为幅值较大的小波变换系数一般是信号的，而幅值较小的小波变换系数在很大程度上是噪声的。因此，找到一个合适的作为阈值，当第j层第k个小波系数ω_{j, k}小于该阈值时，可认为此时ω_{j, k}的主要是由噪声引起的，则将系数ω_{j, k}减小至0；当ω_{j, k}大于该阈值时，认为此时的ω_{j, k}主要是由信号引起的，则将该系数予以保留，从而实现了信噪分离。利用小波变换对2022年8月9日数据干扰信号进行滤除和重构，经过3层小波变换后数据接近正常（图 4）。

5 结语

通过二连浩特地震台井下测震观测异常数据的傅里叶分析和PSD分析结果，并结合干扰发生的时空信息，高效迅速地识别出干扰因素，及时进行排查与处置，保护了地震观测环境，保证了观测数据质量。此外，对干扰数据进行了小波变换，尽可能滤除干扰，使数据清晰可用。

无失真的、完整的观测和记录地震波是测震台站的首要任务。通过对此次二连浩特地震台井下测震观测干扰因素的分析排查可以发现，当观测数据受到不明原因的干扰时，进行相关分析可以有效缩小干扰原因的排查范围，避免排查方向出现错误，提高排查效率。对受干扰数据进行小波变换可以有效地去除大部分干扰的影响，但经过处理的数据无法避免出现失真的情况，故保护地震观测环境，降低环境噪声水平，才是提升观测质量的关键。