0 引言

20世纪90年代，我国开始正式地电场观测。目前，全国观测场地已有100多个。影响地电场观测的因素较多，这使得观测数据的非前兆异常变化较繁复，给后期的数据使用带来诸多不便。为了有效解决此问题，在地电场观测架设时，一般在同方向放置两测道双极距观测，极距多为150—400 m，南京地震台甚至采用了SN、EW向的三极距观测方式。同方向两测道双极距观测可用于检验数据的一致性，也可用于区别近场和远场（Varotsos et al，1991）的数据异常变化。目前，进行地电场数据检验时，一般采用同方向两测道的相关系数（李通等，2020），在地电场数据质量或有效数据的评估中，一般采用相关系数大于0.8作为有效数据。谭大诚等(2014, 2019)给出了优势方位角的计算方法，该计算方法已经列入中国地震局确认的地震预报清单方法。在优势方位角的计算中，主要采取前10阶的周期谱进行计算。笔者认为该方法仍然存在数据挑选问题，采用同方向两测道原始数据计算的相关系数对数据检验虽然有意义，但也存在一定的问题，主要是相关系数反映的是多个频段数据的一致性，与计算窗长有关，不能反映某一变化周期的相关性，因此无法准确给出地电场变化周期的可靠性检验。鉴于此，针对地电场清单方法的数据检验，有必要从地电场的频谱分析出发，给出同方向两测道的谱相关分析。本文尝试采用同方向两测道的数据谱比分析，对观测数据的检验给出新的计算思路。

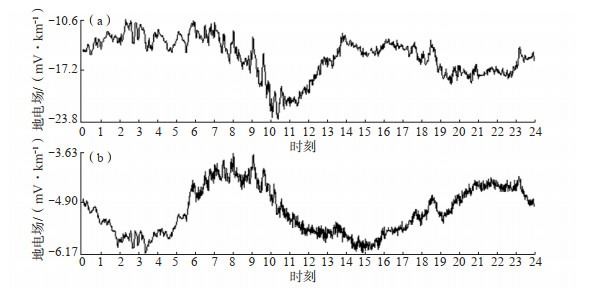
1 地电场的频谱分析

谭大诚等（2010）把地电场的形态特征依据日变化分为2类，即峰—谷波形全天连续的TGF-A型和仅在11时前后出现峰—谷的TGF-B型。在实际观测中，TGF-A型更接近于潮汐变化，观测场地一般离海、湖等较近；更多的场地属于TGF-B型。图 1为江苏新沂地震台、海安地震台地电场观测某一天的数据。由图 1可见，新沂地震台地电场日变主要集中在中午，属于TGF-B型。海安地电场的日变为全天性周期变化，属于TGF-A型。

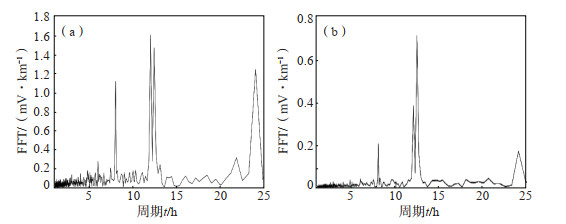
采用傅里叶变换，对新沂地震台、海安地震台2022年5月地电场SN向数据进行谱分析得到图 2。由图 2可见，新沂地震台地电场的频谱前5阶分别为11.80 h、12.20 h、23.22 h、7.91 h、5.95 h，海安地震台地电场的频谱前5阶为12.20 h、11.80 h、23.22 h、7.91 h、5.95 h，周期基本一致，但二者的周期对应振幅不同，前者的前4阶振幅较接近，而后者的半日波变化较突出。分析更多场地后发现，总体来说，TGF-A型、TGF-B型频谱特征的主要区别为周期振幅，TGF-A型的半日波变化较明显，小于8 h的周期振幅相对更小，但周期特征基本一致，依据周期特征进一步对同方向两测道的谱特征相关检验进行分析。

2 同方向两测道的谱特征相关检验

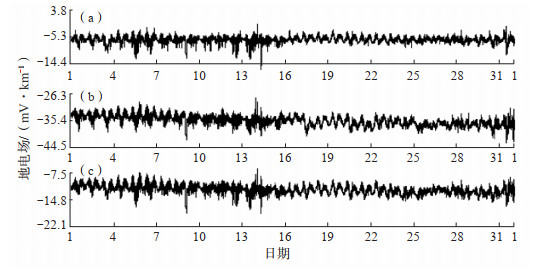
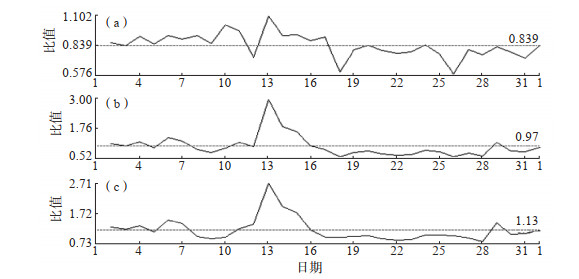
地电场观测时，一般在同一方向架设平行两测向进行观测。数据检验时，一般采用相关系数。判断地电场观测受干扰情况时，常采用同方向两测道地电场测值之比。当观测数据存在系统性问题或观测环境存在明显干扰时，一般会导致同方向两测道地电场测值相关系数的下降和比值变大的情况。同方向两测道的周期谱比值计算也具有类似的意义，但其更侧重于周期的特征变化。图 3为2022年3月南京地震台地电场SN向400 m、200 m、100 m极距的分钟值，该台同方向两测道采用3个不同极距也是为了更好地进行数据检验（李伟等，2010）。由图 3可见，3个极距的地电场原始观测曲线变化存在一定的同步性。利用图 3的数据进行快速傅里叶变换，取前5阶的振幅，然后求取不同极距的振幅比值（图 4）。由图 4可见，比值平均值约为1，但每天的振幅比稍有差异，如2022年4月13日400 m极距与200 m、100 m极距的振幅比偏离较大，而200 m极距与100 m极距的振幅比较合理，故推断400 m极距的观测可能存在问题。由此可见，对于同一方向三测道平行观测，较容易辨别哪个测道观测结果较合理。如果是两测道观测就需要更多的信息进行判断，一般在计算时因无法判断哪道观测更合理，而舍去当日的观测数据。与利用同方向两测道观测数据计算相关系数进行数据检验相比，频谱比值更侧重于周期特征，可以作任何周期段的频谱比值，有时还可以忽略数据的长周期漂移问题，提高数据的利用率。下面讨论可能对频谱比值产生影响的因素。

2.1 降雨的影响

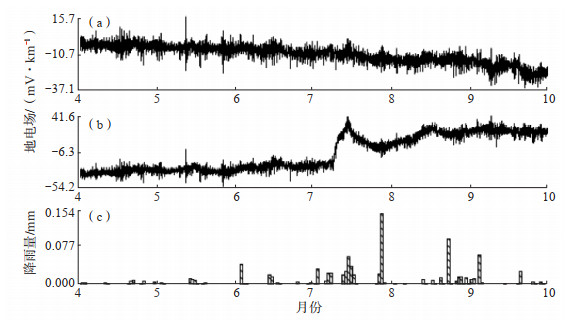
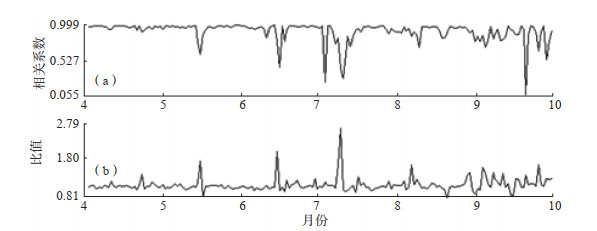
地电场包括大地电场和自然电场2部分，自然电场与场地电性结构、周围环境等有关。实际观测中，降雨或灌溉等是较明显的影响因素。沈红会等（2005）采用同方向两测道观测数据进行相关系数计算时发现，降雨导致相关系数明显下降。图 5为新沂地震台2021年4—9月地电场、降雨量数据。由图 5可见，降雨对地电场观测造成了一定的影响。作同方向两测道观测数据相关分析和谱比分析的结果见图 6。由图 6可见，降雨后相关系数有所下降，相关系数小于0.7的天数有10多天；在相关系数下降的同时，谱比分析的结果也有偏离比值1的情况，但不是所有都偏离，总体上偏离20%以上的情况较少；而相关系数较高的时段，基本上谱比分析结果也较理想。因此，降雨对地电场观测的影响，无论是对原始数据，还是对同方向两测道相关系数均有明显影响。短期降雨对谱比分析结果也有一定的影响，但要小于对相关系数的影响。

2.2 地电扰动的影响

地电场观测仪器记录到自然电场的同时，也记录到变化电场的成分，变化电场与地磁场的变化也是相关的，对于天然场，一般有

$ \begin{array}{*{20}{c}} {{E_x} = {Z_{xx}}{H_x} + {Z_{xy}}{H_y}}\\ {{E_y} = {Z_{yx}}{H_x} + {Z_{yy}}{H_y}} \end{array} $

(1)

其中，Z为地下阻抗张量。因此，地磁场变化较剧烈时，电场也会有相应周期的变化。图 7为高邮地震台地电场SN向测值相关系数、谱比、地磁H分量日变。由图 7可见，同方向两测道测值的变化与地磁变化间存在一定的同步性，在地磁分量变化较大时，同方向两测道测值的相关系数也会较高。对于谱比而言，虽然取的前5阶都是5 h以上的周期，但地磁的短期磁扰变化并没有影响谱比结果，因此，图 7中谱比偏离较大的情况显然与地电场扰动变化无关。

2.3 地铁的影响

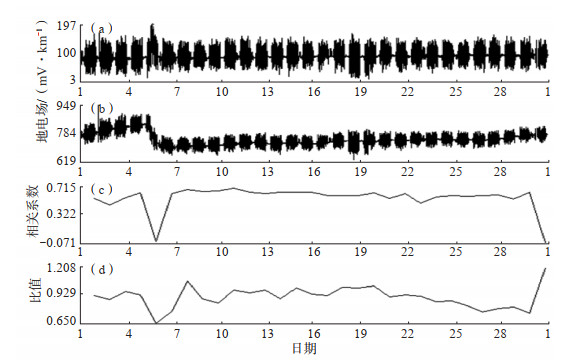
随着经济的发展，城市里的各种干扰对地电场观测产生了较大影响，尤其是地铁干扰，其对地电场观测的影响距离大于30 km。但在实际观测中，南京市区地铁对100 km外的高淳地震台、高邮地震台地电场观测都有较明显的高频噪声影响。地铁对地电场观测的干扰是由地铁运行过程中漏电所产生的，与地铁的启动、加减速等有关，因此，一般干扰频段为秒级至高频，与由谱比计算所得的频段间存在较大差异。图 8为2005年11月南京地震台地电场NE向观测原始数据、相关系数和谱比分析结果。由图 8可见，原始数据受地铁干扰的影响较严重（场地距最近地铁线路仅1 km左右），利用原始数据完全无法进行分析，NE向两测道测值相关系数也较小，基本小于0.7；而谱比分析计算数据仍约为1，这显示地铁干扰对观测结果影响较小。谱比结果较理想也意味着高频干扰对优势方位角计算的影响较小，数据仍具有一定的使用价值。

2.4 频率域、时域内的相关系数对比

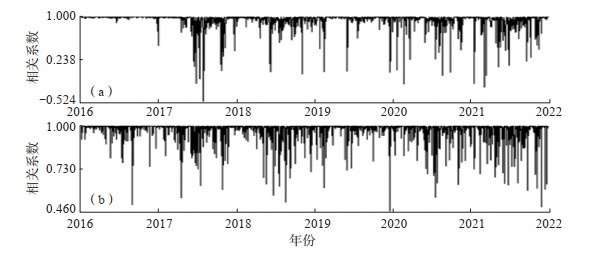
同方向两测道原始数据的相关系数可以理解为时域内的相关系数，同方向两测道原始数据频谱比的相关系数可以理解为频率域内的相关系数，进行频率域、时域内的相关系数对比分析，频率域内仍采用前5阶周期振幅的计算结果，时域内采用原始数据分钟值，窗长均为1天。图 9为高邮地震台2016—2021年地电场EW向两测道测值的频率域、时域内的相关系数对比。由图 9可见，时域内相关系数在长期观测中变化较大，甚至存在少数负相关的情况；频率域前5阶周期振幅的相关系数则较稳定。2016—2021年频率域、时域内的相关系数平均值分别为0.975、0.942，显然频率域内的相关系数较理想，这对于提高观测数据利用率是有利的。

3 讨论与结论

影响地电场观测数据的因素较复杂，包括观测电极、场地周围地下杂散电流、场地水系等等。在实际观测中，很多地震台站的观测数据均存在稳定性问题，因此一般通过同方向2个平行测道观测数据的相关系数来判断数据的质量。在常规的数据处理中，一般选取24 h同方向两测道观测数据的相关系数作为评价依据。但由于相关系数计算主要反映趋势性变化，因此计算窗长不同，计算结果也会有较大不同，尤其是窗长越长，越可能存在相关系数下降的问题。另外，短期的高频干扰也会影响相关系数。采用同方向两测道观测数据的频谱比来评价数据质量或有效数据，相对而言更有针对性，可以根据需要评价任何周期的数据，本文采用的是前5阶周期的计算结果，实际上也可以计算其他周期的比值来判断。这样可以有效解决计算窗长的问题，数据的长期趋势性变化对计算结果影响不大，与地电场的预报清单（中国地震局监测预报司，2020）计算方法和日变处理方法（Ye et al，2018）也较契合。由于只需要部分周期的结果，因此，可以大幅提高有效数据的使用率，如清单方法采用的都是小时以上周期的数据，因此可以忽略一些高频干扰对数据的影响。另外，由于不极化电极存在使用期限问题，因此在地电场观测中需及时更换电极，而采用频谱计算则可使铅电极代替不极化电极成为可能。本文没有给出有效数据的频谱比值范围，这尚需在地震预报实践中进一步给出合理的判断，进而为地电场数据的质量评价提供思路。