2) 中国湖北 430074 长江三峡勘测研究院有限公司(武汉)
2) Three Gorges Geotechnical Engineering Co. Ltd (Wuhan), Hubei Province 430074, China
长期的GNSS(global navigation satellite system)坐标时间序列可以反映测站的运动趋势,从而反映地壳三维运动特征,为地震学、地球动力学等研究提供依据(Blewitt et al,2002;严志文等,2022)。地壳三维运动特征分析的前提是基于GNSS时间序列噪声特性建立准确的速度场(田云锋等,2010)。国内外对GNSS时间序列的噪声特性研究表明,坐标时间序列的噪声主要表现为闪烁噪声加白噪声的组合FNWN(Chen et al,2013;Montillet et al,2013;张风霜,2016)。也有部分研究者认为GNSS各坐标分量的最优噪声模型并非完全是FNWN(Dong et al,2002;姜卫平等,2018)。因此,本文在建立最优噪声模型的基础上,分析赣鄂皖交界地区7个GNSS基准站近10 a的观测数据,获取三维平均速度场和动态变化速度场,研究该地区的三维地壳运动特征,以期为地震趋势判定提供一定的依据。
1 数据采用中国地震局公开的“中国大陆构造环境监测网络”(简称“陆态网络”)赣鄂皖交界地区2010—2020年7个GNSS基准站观测数据,利用gamit/globk10.7同时解算所有GNSS观测数据,获得每日松弛解;然后,通过globk采用七参数转换的方法将松弛解约束到ITRF 2014(International Terrestrial Reference Frame 2014)框架下。所选站点的空间分布如图 1所示。为了获取“干净”的GNSS时间序列,采用IQR(interquartile range)准则对其粗差进行了剔除。

|
图 1 赣鄂皖交界地区GNSS基准站分布站点的颜色表示时间序列的时间长度 Fig.1 Distribution of GNSS reference stations in Jiangxi-Hubei-Anhui junction area |
GNSS坐标时间序列由线性和非线性的函数项和噪声项构成,线性项也被称为趋势项,表示测站速度;非线性项也被称为周期项,表示测站周期性运动趋势(Zhang et al,1997;姜卫平等,2014a)。准确确定GNSS坐标时间序列函数项(即GNSS速度场)的前提是,准确判定坐标时间序列的噪声类型并采用合理的方法估计GNSS坐标时间序列的趋势项。
目前,极大似然估计(Zhang et al,2002;姜卫平等,2018)是GNSS坐标时间序列的最优分析方法之一。该方法能同时确定噪声模型、周期项、测站速度及其中误差。该方法的参数模型一般由下式表示(黄立人,2006;Bos et al,2013;张风霜,2016;贺小星等,2017)
| $ y\left(t_i\right)=y_0+v t_i+\sum\limits_{k=1}^q\left[a_k \sin \left(2 \pi f_k t_i\right)+b_k \cos \left(2 \pi f_k t_i\right)\right]+\sum\limits_{j=1}^{n_g} g_j H\left(t_i-T_{g j}\right)+\varepsilon\left(t_i\right) $ | (1) |
式中,y (ti)为坐标序列;y0表示初始位置;ti为时间,单位为a,1 a被认为是365.25 d;v为线速度,即线性趋势项;ak、bk为周期项系数;fk为相应频率;gj、Tgj分别为阶跃及对应的历元;ε(ti)为噪声项,即噪声模型,为噪声分析的主要对象;H为Heaviside函数,用下式表示
| $ \left\{\begin{array}{l} H(t)=0, t<0 \\ H(t)=0.5, t=0 \\ H(t)=1, t>0 \end{array}\right. $ | (2) |
在应用极大似然估计方法进行噪声分析建立时间序列速度场之前,噪声模型预先假定。分别假定的噪声模型包括白噪声WN、幂律噪声PL、闪烁噪声FN、随机游走噪声RW、一阶高斯马尔可夫噪声GGM,以及它们之间的两两组合。如FNWN表示闪烁噪声加白噪声组合,是GNSS坐标序列噪声分析最常见的噪声组合。
极大似然估计能同时确定噪声模型、周期项、测站速度及其中误差。根据贝叶斯信息准则(BIC)可以确定最优的噪声组合模型,其定义如下(Bierens,2004)
| $ \mathrm{BIC}=-2 \ln L+k \ln n $ | (3) |
式中,L为某一模型下的似然函数;n为观测值个数;k为模型的变量个数。根据BIC准则,BIC值越小,对应的模型越真实,噪声模型越优(姜卫平等, 2013, 2014b),估计的测站速度最准确。
3 结果与分析采用前述的速度场估计方法,分别对赣鄂皖交界地区的7个GNSS基准站2010年10月至2013年12月、2014年1月至2016年12月、2017年1月至2020年12月、2010年10月至2020年12月的坐标时间序列进行噪声分析,建立速度场,分析该地区的三维地壳运动特征。
3.1 噪声分析结果应用极大似然估计方法,通过BIC准则估计的三坐标分量最优噪声模型统计结果见表 1。
| 表 1 7个测站、4个时间跨度坐标序列最优噪声模型 Table 1 Optimal noise model for 4 time-span coordinate time series of 7 stations |
从表 1可知:①分析的7个测站、4个时间跨度三分量坐标序列主要为闪烁噪声加白噪声FNWN特性,约占61.9%,这与已有研究成果相吻合(Chen et al,2013;Montillet et al,2013);②每个测站同一时间跨度坐标序列表现的噪声特性不尽相同,如AHAQ、FJWY、HNLY、ZJJD站E分量最优噪声模型均为闪烁噪声加白噪声组合FNWN,而JXHK、JXJA、WUHN站最优噪声模型分别为幂律噪声加白噪声PLWN、一阶马尔可夫噪声加白噪声GGMWN、随机游走噪声加闪烁噪声和白噪声RWFNWN;③同一测站的不同时间跨度的噪声特性也会有变化,如JXHK站2010年10月-2013.12E分量的最优噪声特性表现为幂律噪声加白噪声PLWN,而2014年1月至2016年12月的最优噪声特性变现为随机游走噪声加白噪声RWWN;④在时间跨度为10 a以上的时间序列中,3个坐标分量的最优噪声特性主要表现为闪烁噪声加白噪声FNWN和幂律噪声加白噪声PLWN,占比分别为47.6%、23.8%,其他噪声模型占比较少。
3.2 速度场结果在准确确定测站时间序列的最优噪声模型的前提下,才能准确估计测站的线性趋势及周期项,为测站建立真实准确的速度场。根据3.1节确定的最优噪声模型,采用极大似然准则估计了2010年10月至2013年12月(d1)、2014年1月—2016年12月(d2)、2017年1月—2020年12月(d3)及2010年10月—2020年12月(d4)等4个时间段7个测站的速度场,结果如表 2所示。
| 表 2 各测站各时间跨度速度场及其中误差(单位:mm/a) Table 2 Velocity fields and their errors in each time span of each station (unit: mm/a) |
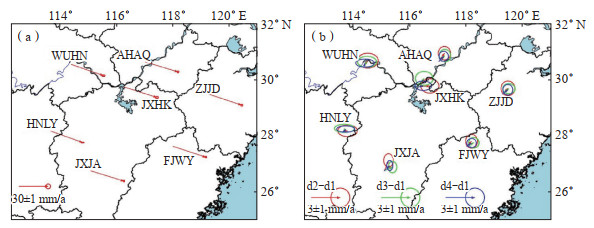
从表 2可知:①7个测站4个时间跨度水平方向运动趋势基本一致,均向东南方向线性运动,东方向速度约为(33.3±0.2)mm/a,南方向速度约为(11.5±0.1)mm/a,该速度场可反应赣鄂皖交界地区的水平地壳运动,7个测站2010年10月至2020年12月的水平运动速度场如图 2(a)所示;②从中误差来看,水平方向3 a时间跨度的坐标序列中误差约为±0.4 mm,10 a的为±0.1 mm;③垂直方向的速度与中误差处于同一量级,并不能反应测站运动趋势上升还是下降,需要其他观测数据如精密水准测量观测资料才能进行判断。
|
图 2 2010年10月至2020年12月7个测站4个时段GNSS时间序列水平速度场及其差异 (a)d1时段时间序列速度场;(b)d2、d3、d4与d1时段间速度场差异 Fig.2 Horizontal velocity fields and their differences of GNSS time series in 4 time periods at 7 stations from October 2010 to December 2020 |
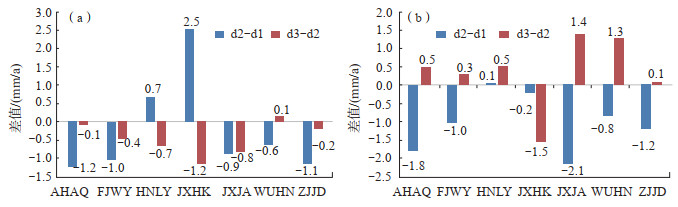
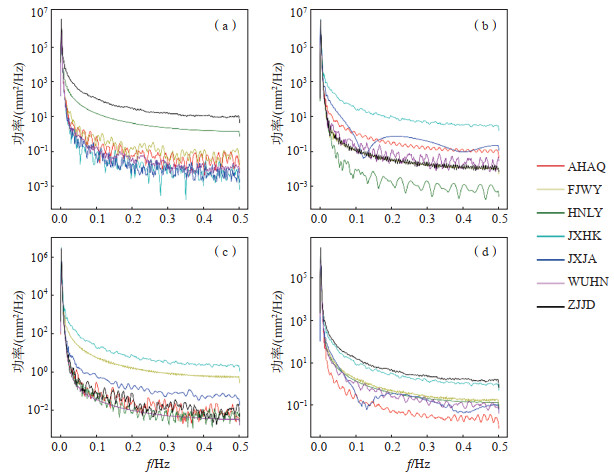
为分析各个测站水平运动的动态变化,将d2坐标序列速度场减去d1坐标序列的速度场获得差值d2-d1,将d3的坐标序列减去d1的坐标序列获得差值d3-d1,将d4坐标序列的速度场减去d1的速度场获得差值d4-d1,各速度场差异如图 2(b)所示。E、N分量的d2-d1、d3-d2速度差值如图 3所示。由图 3可见,差值为正值表示后一时间跨度的速度场较前一时间跨度的速度场大,说明线性运动速度变大;反之,线性速度变小。由图 3(a)可知,AHAQ、FJWY、JXJA、ZJJD站东方向线性运动速度变小,其他测站并无单一的速度变化趋势;由图 3(b)可知,HNLY站向南线性运动的速度变大,JXHK站向南线性运动的速度变小,其他测站并无单一的速度变化趋势。7个GNSS测站垂直方向的周年、半周年振幅及中误差如表 3所示,welch功率谱如图 4所示。经计算7个测站4个时段垂直分量的线性趋势项及年周期、半年周期信号频率,并由图 4可知,7个测站在垂直方向上均有较强的低频年周期、半周年信号,无明显线性项和其他高频率信号。
|
图 3 7个测站4个时间跨度GNSS时间序列水平速度场差值 (a)E分量坐标序列;(b)N分量坐标序列 Fig.3 GNSS time series horizontal velocity field differences of 7 stations and 4 time spans |
| 表 3 各测站各时间跨度垂直方向周期振幅及其中误差(单位:mm) Table 3 Periodic amplitudes and their errors in the vertical direction of each station and each time span |
|
图 4 7个测站4个时段垂直分量功率谱 Fig.4 Vertical component power spectrum of 7 stations and 4 periods (a)d1;(b)d2;(c)d3;(d)d4 |
利用2010年10月至2020年12月GNSS观测资料研究赣鄂皖交界地区三维地壳运动特征,得到以下结论。
(1)7个测站短时间跨度(3 a)三分量坐标序列主要为闪烁噪声加白噪声FNWN特性,约占61.9%,同时,每个测站同一时间跨度坐标序列表现的噪声特性不尽相同,且同一测站不同时间跨度的噪声特性也有所不同。在时间跨度为10 a以上的时间序列中,3个坐标分量的最优噪声特性主要表现为闪烁噪声加白噪声FNWN和幂律噪声加白噪声PLWN,占比分别为47.6%、23.8%。
(2)水平运动均呈现向东南方向的线性运动趋势。东方向速度场分量平均值为(33.3±0.2)mm/a,南方向为(11.5±0.1)mm/a。AHAQ、FJWY、JXJA、ZJJD站东方向线性运动速度变小,HNLY站向南线性运动速度变大,JXHK站向南线性运动速度变小。
(3)垂直方向呈现明显的周年、半周年周期运动。周年平均振幅为(3.2±0.7)mm,半周年为(1.0±0.4)mm。GNSS观测结果表明该地区垂直方向并未呈现明显的线性运动特征。
贺小星, 花向红, 鲁铁定, 等. 时间跨度对GPS坐标序列噪声模型及速度估计影响分析[J]. 国防科技大学学报, 2017, 39(6): 12-18. |
黄立人. GPS基准站坐标分量时间序列的噪声特性分析[J]. 大地测量与地球动力学, 2006, 26(2): 31-33. |
姜卫平, 李昭, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列非线性变化的成因分析[J]. 地球物理学报, 2013, 56(7): 2 228-2 237. |
姜卫平, 夏传义, 李昭, 等. 环境负载对区域GPS基准站时间序列的影响分析[J]. 测绘学报, 2014a, 43(12): 1 217-1 223. |
姜卫平, 周晓慧. 澳大利亚GPS坐标时间序列跨度对噪声模型建立的影响分析[J]. 中国科学(地球科学), 2014b, 44(11): 2 461-2 478. |
姜卫平, 王锴华, 李昭, 等. GNSS坐标时间序列分析理论与方法及展望[J]. 武汉大学学报(信息科学版), 2018, 43(12): 2 112-2 123. |
田云锋, 沈正康, 李鹏. 连续GPS观测中的相关噪声分析[J]. 地震学报, 2010, 32(6): 696-704. |
严志文, 李征, 杨腾飞. 基于GNSS数据的地震电离层扰动探测分析[J]. 地理空间信息, 2022, 20(4): 134-138. |
张风霜. 有色噪声模型下云南地区GPS基准站速度与周期估计[J]. 地震研究, 2016, 39(3): 410-420. |
Bierens H J. Information criteria and model selection[J]. Pennsylvania State University, 2004, 1(3): 2-6. |
Blewitt G, Lavallée D. Effect of annual signals on geodetic velocity[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B7): ETG 9-1-ETG 9-11. |
Bos M S, Fernandes R M S, Williams S D P, et al. Fast error analysis of continuous GNSS observations with missing data[J]. Journal of Geodesy, 2013, 87(4): 351-360. |
Chen Q, van Dam T, Sneeuw N, et al. Singular spectrum analysis for modeling seasonal signals from GPS time series[J]. Journal of Geodynamics, 2013, 72: 25-35. |
Dong D, Fang P, Bock Y, et al. Anatomy of apparent seasonal variations from GPS-derived site position time series[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B4): ETG 9-1-ETG 9-16. |
Montillet J P, Tregoning P, McClusky S, et al. Extracting white noise statistics in GPS coordinate time series[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(3): 563-567. |
Zhang F P, Dong D, Cheng Z Y, et al. Seasonal vertical crustal motions in China detected by GPS[J]. Chinese Science Bulletin, 2002, 47(21): 1 772-1 780. |
Zhang J, Bock Y, Johnson H, et al. Southern California permanent GPS geodetic array: Error analysis of daily position estimates and site velocities[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18 035-18 055. |
 2023, Vol. 44
2023, Vol. 44

