2) 中国呼和浩特 010010 内蒙古自治区地震局
2) Earthquake Agency of Inner Mongolia Autonomous Region, Huhhot 010010, China
地震波形记录易受外界因素干扰,这在一定程度上影响了对地震事件识别分析的有效性和准确性(曾宪伟等,2010)。在实际地震观测中,经常可以记录到以工业爆破为主的人工小爆破(以下简称爆破),因其波形与天然地震波形较相似,影响了地震观测记录的质量,而且通过宏观特征很难将其排除或识别。此外,不同分析人员的识别结果也存在差异。如果不能及时剔除爆破的波形记录,会混淆地震目录,影响相关地震学研究工作。因此,准确区分爆破与天然地震,并制定出相应的定量或定性的识别判据,对于地震监测和地震分析预报工作十分重要。
目前国内已开展识别天然地震与爆破的相关研究。霍祝青等(2015)通过波形对比、震幅比、频谱等方法研究了天然地震与爆破;高云超(2005)利用希尔伯特—黄变换方法进行仿真研究;黄汉明等(2010)利用4层小波包变换提取出不同长度的香农熵特征进行天然地震与爆破的相关研究;王婷婷等(2011)提出快速识别天然地震与人工爆破的5种判据。本文基于阿尔山火山地震观测站典型的天然地震、爆破波形记录特征,针对天然地震波形与爆破波形易混淆的问题,在分析天然地震波形和人工爆破信号的时域、频域特征的基础上,采用希尔伯特变换(Hilbert transform,HHT)方法,对原始波形信号进行EMD分解,提取最大幅值对应的周期、倒谱平均值、自相关函数的最大值,进行特征分析,以期为阿尔山火山地震观测站天然地震与爆破的识别提供参考依据。
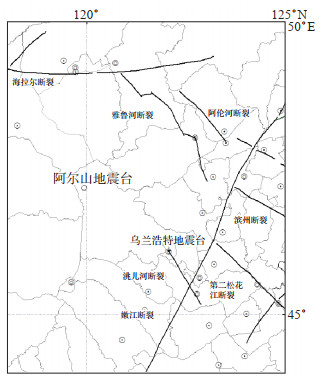
1 资料的选取阿尔山火山地震观测站台基为花岗岩,台站高程1 069 m,是国家无人值守地震台,负责全球地震观测任务(图 1)。阿尔山火山地震观测站测震仪器(CTS-1E型)摆放在摆房内,易受自然环境影响(席文雅等,2020)。整理2020年12月至2022年8月阿尔山火山地震观测站记录的100个地震事件、100个爆破事件进行特征分析(图 2)。
|
图 1 阿尔山火山地震观测站位置 Fig.1 Location of Arshan Volcano Seismic Station |

|
图 2 100个地震事件、100个爆破事件的时间分布 Fig.2 Time distribution of one hundred seismic events and one hundred blasting events |
希尔伯特—黄变换(HHT)是一种处理非线性、非平稳信号的有效方法(杨培杰等,2007)。其适应性好,具有更明确的时频描述、更有效的滤波性能,可用于各种数据的分析、处理及实时计算,目前已用于非线性系统分析、潮汐和海啸分析、海洋环流分析、水波分析、风速分析、地震信号分析、医学信号分析、结构土木工程、环境科学分析、故障诊断等领域(毕明霞等,2011)。希尔伯特—黄变换以瞬时频率为表征信号变化的基本量,它主要由经验模态分解和希尔伯特谱分析2部分组成。
2.2 经验模态分解经验模态分解(empirical mode decomposition,简称EMD)是希尔伯特—黄变换中的关键方法。它根据信号本身的时间尺度特征来对信号进行分解,由信号的自适应基将信号分解为包含不同时间尺度的局部特征信号,且分解过程中不需要像小波一样选择合适的正交基,对外界的依赖性较小,分解后的每一个分量即内模函数(intrinsic mode function,简称IMF)。EMD分解是一种分析非平稳、非线性信号的有效方法,具有较好的信噪比,它能够对非平稳信号进行平稳化处理(毕明霞等,2011),具体步骤如下。
(1)求出原信号序列S(t)的局部极大值和局部极小值。
(2)利用3次样条曲线插值连接局部极大值和局部极小值,分别得到局部极大值对应的上包络线Smax(t)和局部极小值点对应的下包络线Smin(t)。
(3)对每个时刻的Smax(t)、Smin(t)取平均值m(t),即
| $ m(t)=\frac{\left[S_{\max }(t)+S_{\min }(t)\right]}{2} $ | (1) |
(4)用原信号序列S(t)减去每个时刻对应的瞬时平均值m(t),即
| $ h(t)=S(t)-m(t) $ | (2) |
这样得到的h(t)就是一个去掉了低频的新的信号序列。
(5)检查h(t)是否符合IMF函数所应满足的2个条件。如果满足,则h(t)即为IMF函数;若不满足,则需要将h(t)作为原信号序列重复上述4个步骤,直到满足IMF的2个条件为止,这样得到的第1个IMF,记为C1(t),C1(t)代表了原信号序列中的高频部分。
(6)将C1(t)从原信号序列中分离出来,即
| $ S(t)-C_1(t)=r_1(t) $ | (3) |
r1(t)仍包含较长周期分量,因此将r1(t)作为新的时间序列用同样的方法进行处理,即
| $ \begin{aligned} & r_1(t)-C_2(t)=r_2(t) \\ & r_2(t)-C_3(t)=r_3(t) \\ & \ldots \\ & r_{n-1}(t)-C_n(t)=r_n(t) \end{aligned} $ | (4) |
直到rn(t)变成单调函数或常数,再没有IMF被分解出来为止。
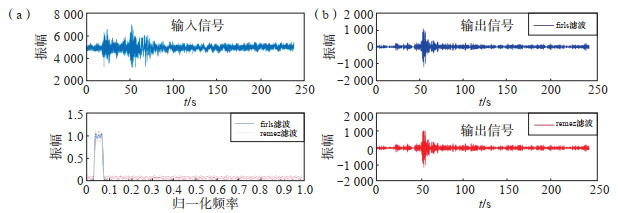
3 结果与分析 3.1 数据预处理在地震数据记录过程中,会受到周边环境的干扰,所以首先对地震、爆破数据进行预处理,处理后的天然地震、爆破波形更加清晰(图 3、4)。
|
图 3 天然地震的原始波形(a)和预处理后的波形(b) Fig.3 The original (a) and preprocessed (b) waveforms of natural earthquakes |

|
图 4 爆破的原始波形(a)和预处理后的波形(b) Fig.4 The original (a) and preprocessed (b) waveforms of blasting event |
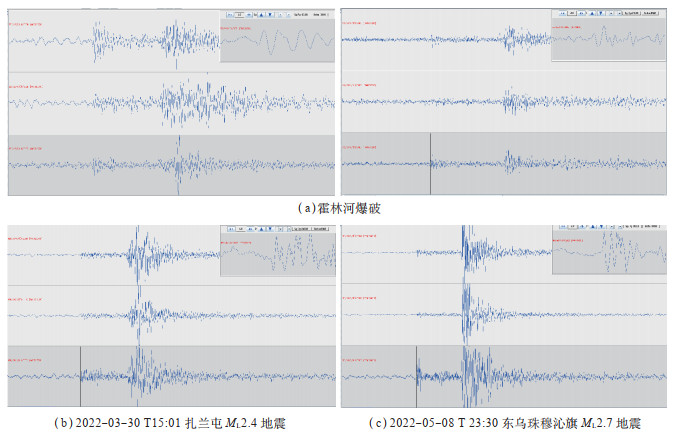
整理2020年12月至2022年8月阿尔山火山地震观测站记录的天然地震、人工爆破的原始波形发现,爆破P波初动强而尖锐,初动方向向上[图 5(a)];由2022年3月30日15:01扎兰屯ML 2.4、5月8日23:30东乌珠穆沁旗ML 2.7地震的波形可见[图 5(b)],P波初动尖锐,呈脉冲形状;从垂直方向波形来看,地震波初动方向可能向上,也可能向下,面波周期比爆破的短,地震较爆破衰减慢(刘瑞丰等,2014)。
|
图 5 人工爆破(a)与天然地震(b)、(c)的原始波形 Fig.5 Artificial blasting (a) and original waveforms of natural earthquakes (b) (c) |
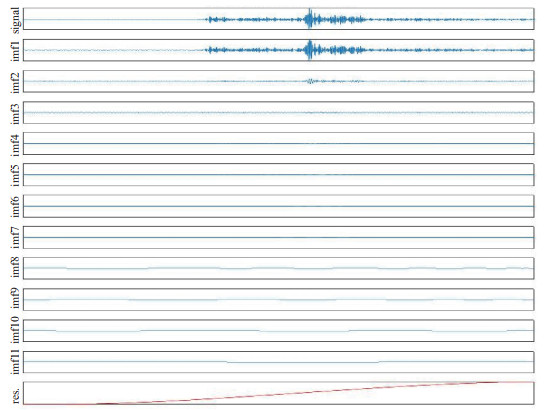
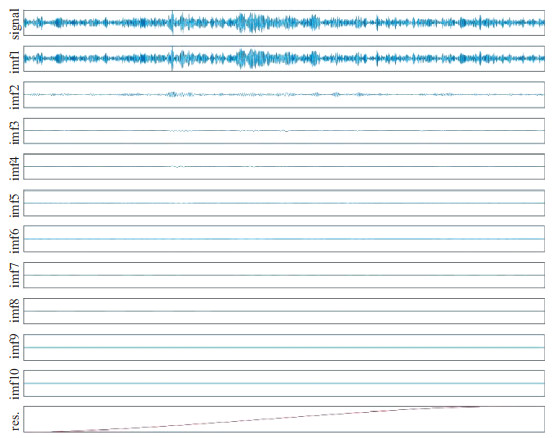
使用MATLAB软件,将预处理后的100个天然地震和100个爆破进行EMD分解,其中,由1个天然地震得到11个IMF和1个趋势项(图 6),由爆破得到10个IMF和1个趋势项(图 7)。
|
图 6 天然地震的EMD分解 Fig.6 EMD decomposition of natural earthquakes |
|
图 7 人工爆破的EMD分解 Fig.7 EMD decomposition of artificial blasting |
本研究只对EMD分解后的前3个IMF分量进行希尔伯特变换,然后,基于HHT方法来提取特征值,特征值分别是最大幅值对应的周期(Tamax)、倒谱平均值(Cave)和自相关函数的最大值(Mxc)。最大幅值对应的周期(Tamax)就是IMF幅值最大处的样本点的瞬时频率的倒数,使用语句[amax3, idex3] = max [c(m, : )];Tamx = 1./f (m, idex3)可以得到,其中,m表示第m个IMF分量;idex3表示IMF分量中最大幅值的相对位置;倒谱的定义是功率谱的对数值的逆傅氏变换,倒谱平均值(Cave)就是所有信号记录点的倒谱值相加的和与记录长度的比值,可以用语句[rc, rcm = rceps[c(m, : )];Cave = sum[rc(1, : )]/length(rc)]得到;而自相关函数的最大值(Mxc)在MATLAB软件上可以用语句maxx = max[xcorr(c(m, : ))]得到,最后得到1个1×9维的特征向量空间F
| $ \boldsymbol{F}=\left[\left(T_{\text {amax}1}, C_{\text {ave}1}, M_{\mathrm{xc1}}\right), \left(T_{\text {amax}2}, C_{\text {ave}2}, M_{\mathrm{xc}2}\right), \left(T_{\text {amax}3}, C_{\text {ave}3}, M_{\mathrm{xc3}}\right)\right] $ | (5) |
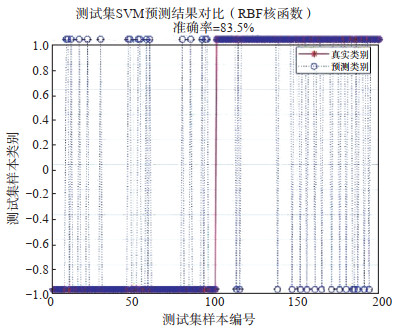
支持向量机(support vector machine,简称SVM)是在统计学习理论基础上发展起来的一种在高维空间上使用线性函数的假设空间学习系统(周海军,2012)。使用基于SVM的交叉验证方法对由阿尔山火山地震观测站100个天然地震和100个爆破提取的特征值进行分类实验,特征值分别是最大幅值对应的周期(Tamax)、倒谱平均值(Cave)、自相关函数的最大值(Mxc),共200×3个特征值,再随机抽取100×3个特征值进行识别验证,结果见表 1、图 8、图 9。
| 表 1 分类实验结果 Table 1 Classification of experiment results |
|
图 8 由第3个IMF分量提取的特征值(200×3)的识别图 Fig.8 Recognition diagram of the eigenvalues (200×3) extracted by the third IMF component |

|
图 9 由第3个IMF分量提取的200×3特征值(a)、100×3特征值(b)的识别准确率 Fig.9 Recognition accuracy of 200×3 eigenvalues (a) and 100×3 eigenvalues (b) of the third IMF component extracted |
通过对阿尔山火山地震观测站100个天然地震和100个人工爆破进行特征分析,得到如下结论。
(1)人工爆破特征:P波初动强而尖锐,初动方向向上,周期较短,振动衰减较快;天然地震特征:P波初动尖锐,呈脉冲形状,面波周期比爆破的短,地震较爆破衰减慢。
(2)希尔伯特—黄变换(HHT)能够很好地分析天然地震和人工爆破。
(3)预处理后的天然地震、爆破波形变化明显,由此可见,阿尔山火山地震观测站受周边环境干扰严重。
(4)利用最大幅值对应的周期Tamax、倒谱平均值Cave、自相关函数的最大值Mxc能够较好地识别天然地震、人工爆破波形信号的有效特征。
(5)基于SVM交叉验证方法进行识别,由第2、3个IMF分量提取的特征值识别率较高,达80%以上。研究结果可为在阿尔山火山地震观测站识别天然地震和人工爆破提供依据。
毕明霞, 黄汉明, 边银菊, 等. 天然地震与人工爆破波形信号HHT特征提取和SVM识别研究[J]. 地球物理学进展, 2011, 26(4): 1 157-1 164. |
高云超. 希尔伯特—黄变换方法的仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2005.
|
黄汉明, 边银菊, 卢世军, 等. V-SVC算法在地震与爆破识别及窗长度选取中的应用[J]. 地震地磁观测与研究, 2010, 31(3): 24-31. |
霍祝青, 王俊, 张金川, 等. 江苏地区天然地震与人工爆破识别研究[J]. 地震工程学报, 2015, 37(1): 228-231. |
刘瑞丰, 陈翔, 沈道康, 等. 宽频带数字地震记录震相分析[M]. 北京: 地震出版社, 2014: 252.
|
王婷婷, 边银菊. 识别天然地震和人工爆破的判据选择[J]. 地震地磁观测与研究, 2011, 32(6): 62-67. |
席文雅, 贾宝金, 刘芳, 等. 乌兰浩特地震台与阿尔山火山地震观测站面波震级偏差分析[J]. 地震地磁观测与研究, 2020, 41(1): 8-12. |
杨培杰, 印兴耀, 张广智. 希尔伯特-黄变换地震信号时频分析与属性提取[J]. 地球物理学进展, 2007, 22(5): 1 585-1 590. |
曾宪伟, 赵卫明, 李鸿庭, 等. 利用小波包变换时频谱识别宁夏及邻区的地震和爆破[J]. 地震研究, 2010, 33(3): 300-307. |
周海军. 基于地震波形的震源类型自动识别研究[D]. 桂林: 广西师范大学, 2012.
|
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1 971): 903-995. |
 2023, Vol. 44
2023, Vol. 44


