准确可靠的地震序列参数是构建可操作的余震预测(Operational Aftershock Forecast,OAF)模型和快速实施震后余震预测、序列类型判定、危险性评估的基础。震后初期余震数量指数级增长,大量小地震“淹没”在大地震中而无法被及时识别出来,造成余震数量的大量缺失,导致一些依赖完整性震级的预测模型无法发挥其效能。而震区应力调整使得震后数小时至数天内的序列参数变化剧烈,且受到初值选择的严重制约。Omi等(2013)发展了一种可充分利用不完整地震记录并在震后极短期内快速开展参数拟合的Omi-R-J方法,蒋长胜等(2018)、Bi等(2020)将其用于2017年四川九寨沟MS 7.0地震和2008年四川汶川MS 8.0地震中,并与其他模型(ETAS模型、R-J模型)做了对比分析,发现Omi-R-J方法在震后初期能获得更为可靠的序列参数。2021年以来,中国的大陆地区强震之后相继发生多次强余震,如2021年5月21日云南漾濞MS 6.4地震之后的MS 5.2强余震,2021年5月22日青海玛多MS 7.4之后的MS 5.1强余震、2022年1月8日青海门源MS 6.9地震之后的MS 5.2强余震。
2 研究方法Omi等(2013)在R-J模型的基础上,将地震序列早期阶段完整性震级以下的余震考虑到参数拟合中,提出“Omi-R-J”模型。基于OK1993模型,给出对地震事件记录不完整部分检测程度的检测率函数q(M),可表示为
| $ q(M \mid \mu, \sigma)=\frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }} \sigma^2}} \int_{-\infty}^M \mathrm{e}^{-\frac{(x-\mu)^2}{2 \sigma^2} \mathrm{dx}} $ | (1) |
式中,参数μ表示在检测率为50%时的对应震级,σ表示检测到的震级范围。而实际记录的地震概率密度函数可表示为
| $ P(M \mid \beta, \mu, \sigma)=\frac{\mathrm{e}^{-\beta M} q(M \mid \mu, \sigma)}{\int_{-\infty}^{+\infty} \mathrm{e}^{-\beta M} q(M \mid \mu, \sigma) \mathrm{d} M}=\frac{\mathrm{e}^{-\beta M} q(M \mid \mu, \sigma)}{\mathrm{e}^{\left(-\beta \mu+\beta^2 \sigma^2 / 2\right)} / \beta}=\beta \mathrm{e}^{-\beta(M-\mu)+\beta^2 \sigma^2 / 2} q(M \mid \mu, \sigma) $ | (2) |
式中,β = bln10。
参数可由最大似然函数
| $ \ln L(k, c, p)=\sum\nolimits_{M_i \geqslant M_{\mathrm{c}}} \ln v\left(t_i, M_i\right)-\int_{M_{\mathrm{c}}}^{\infty} \mathrm{d} M \int_0^T \mathrm{~d} t v(t, M) $ | (3) |
式中,ti和Mi表示模型拟合“学习时段”[0, T]内发生的第i个余震的发震时刻与震级。
3 研究结果 3.1 序列参数的稳定性分析利用Omi-R-J方法,对2022年1月8日青海门源MS 6.9地震、2021年5月22日青海玛多MS 7.4地震、2021年5月21日云南漾濞MS 6.4地震进行连续、滑动拟合,拟合开始时间自震后0.05天开始,以0.05天步长,持续增加至10.00天,共进行100个时段的滑动拟合。拟合获得的p值、c值、k值以及b值随序列持续时间的变化见图 1。在地震序列早期,3个地震序列参数均变化较为剧烈,相应标准差数值范围也较大,这种剧烈变化反映了主震发生后震源区应力的快速调整过程。地震序列稳定时段,青海门源MS 6.9地震模型参数为p = 0.8428±0.0229、c = 0.0021±0.0024、k = 0.0051±0.0023、b = 0.8200±0.0273;青海玛多MS7.4地震模型参数分别为p = 1.0047±0.0187、c = 0.0094±0.0025、k = 0.0067±0.0020、b = 0.8181±0.0221;云南漾濞MS 6.4地震模型参数分别为p = 1.0767±0.0259、c = 0.0398±0.0105、k = 0.0288±0.0060、b = 0.7549±0.0156。青海门源序列参数变化较为稳定,p值相对较小,地震序列衰减相对较慢;青海玛多序列较为正常,发震4天后序列基本达到稳定状态;云南漾濞地震早期序列参数变化较为剧烈,达到稳定所需时间较长,其b值较小而k值相对较大,可能与其较为发育的余震和强余震有关。

|
图 1 3次地震序列Omi-R-J模型拟合参数随序列持续时间的变化 (a)青海门源MS 6.9地震;(b)青海玛多MS 7.4地震;(c)云南漾濞MS 6.4地震 Fig.1 The Omi-R-J model parameters against the duration time (since the mainshock occurred) in fitting three earthquake sequences |
基于稳定时段的序列参数,分别选取其邻近参数作为初值,利用控制变量法,即改变模型中的单一初值判断对序列参数的影响,自0.05天开始,分别进行11次拟合。考虑到c、k值较小,取对数处理,结果见图 2。
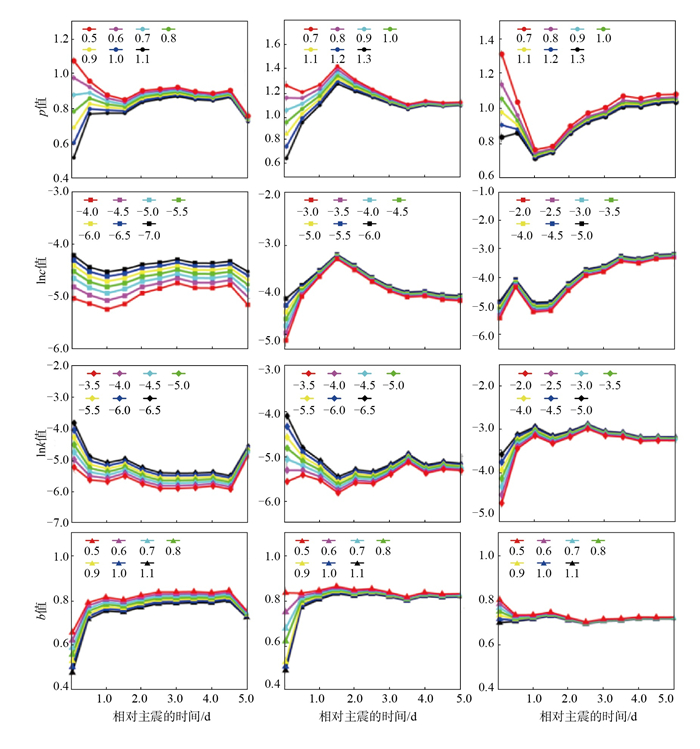
|
图 2 初值选取对地震序列参数的影响 (a) 青海门源MS 6.9地震;(b)青海玛多MS 7.4地震;(c)云南漾濞MS 6.4地震 Fig.2 Influence of initial value selection on parameters of an earthquake sequence |
总体看,参数初值的选取对0.05天的参数拟合影响较大,随着时间推移对序列参数的影响逐渐减弱。此外,p值受初值的影响最为显著,且影响时间较长,当去除因取对数产生的放大效应外,c、k、b值在震后1天内受到一定程度的影响,随着时间的推移,初值对Omi-R-J模型后续参数影响逐渐变小。作为具有减灾重大意义的震后初期(24小时内)的余震预测工作,选取合适的初值作为输入信息,才能更为真实地反映序列初期性质。
4 结束语震后早期地震序列参数包含大量的震源、地质构造以及地球物理特征等信息,参数变化反映了应力的调整状态、序列的活动特性以及余震的活动水平等特征。初值的选取对震后初期极短时间内的参数影响较大,或以相同构造带、相同地壳属性等条件下的参数平均值作为先验信息,可为最大限度地降低初值对序列参数的影响提供一种思路。
日本东京大学生产技术研究所Takahiro Omi博士为本研究提供了程序和技术支持,在此表示感谢。
蒋长胜, 毕金孟, 王福昌, 等. 利用早期余震预测的Omi-R-J方法对2017年四川九寨沟MS 7.0地震的应用研究[J]. 地球物理学报, 2018, 61(5): 2099-2110. |
Bi J M, Jiang C S. Comparison of early aftershock forecasting for the 2008 Wenchuan MS 8.0 earthquake[J]. Pure and Applied Geophysics, 2020, 177: 9-25. |
Omi T, Ogata Y, Hirata Y, et al. Forecasting large aftershocks within one day after the main shock[J]. Scientific Reports, 2013, 3: 2218. |
 2022, Vol. 43
2022, Vol. 43

