1 研究背景

b值为震级—频度统计关系中地震大小与频度分布的斜率，最早由Gutenberg和Richter（1944）提出，后有学者通过岩石模拟实验发现介质的不均匀性和应力状态是导致b值变化的主要因素，该发现为b值在地震预测研究中的应用建立了物理基础。b值用于地震预测研究始于20世纪70年代，研究者发现强震前震中附近b值多存在明显的时空变化特征，低值异常尤为普遍，因此认为b值时空扫描结果可应用于强震预测。前人研究主要聚焦于中强地震前b值的时空变化特征，而对于地震序列强余震前的b值变化研究甚少。而2022年1月2日云南宁蒗M_S 5.5地震序列b值在强余震前变化显著，可见序列强余震前b值变化特征也值得深入研究。

2 研究内容及方法

利用2022年1月2日云南宁蒗M_S 5.5地震序列目录，计算序列b值，进一步分析其随时间演化过程，旨在分析强余震前序列b值的变化特征。

Gutenberg-Richter幂律关系式log₁₀N = a – bM中，N是大于或等于M震级的累积次数，a和b是常数。参数a代表地震产生率，参数b代表地震的相对大小分布。最小二乘法和最大似然法为计算b值的常用方法，但最大似然法（Aki，1965）具有计算简便、不易受个别较大地震影响、计算结果较为稳定的优点，因此，本文使用该方法计算b值。计算公式如下

$b=\frac{\log \mathrm{e}}{M-\left(M_{\mathrm{c}}-\Delta M / 2\right)}$

(1)

式中：M为震级；ΔM为震级分档，文中取0.1；e为自然对数的底数。

b值误差计算公式为

$\delta b=2.3 b^2 \sqrt{\frac{\sum_{i=1}^n\left(M_i-\bar{M}\right)^2}{n(n-1)}}$

(2)

式中：M为平均震级，n为计算b值所用样本量。

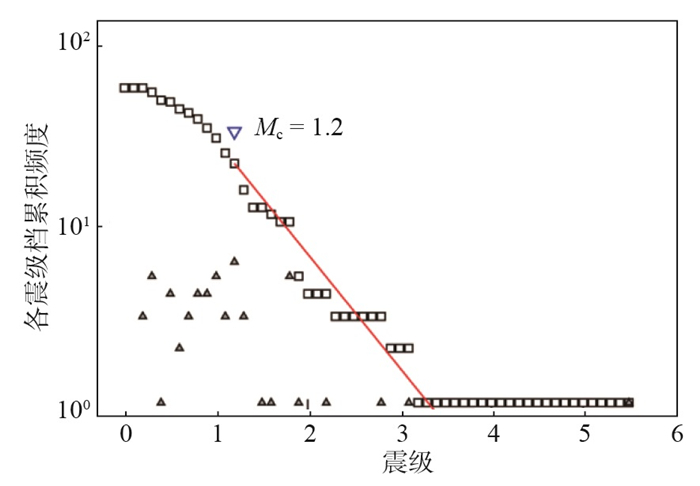
3 研究结果 3.1 最小完整性震级计算

在地震活动研究中，统计分析占较大比重，为了客观研究地震活动规律，应尽可能使用完整的地震记录，即应使用大于最小完整性震级的地震目录开展相关研究。根据序列参数计算要求，主震后第一个24 h内发生地震的最小完整性震级M_c的确定尤为重要，对结果的可信程度有较大影响。因此，取1月2日15时02分M_S 5.5地震后24 h内地震目录，使用Zmap程序，采用最大曲率法计算M_c。计算结果显示，主震发生后24 h内最小完整性震级M_c为1.2（图 1）。

3.2 序列b值变化特征及误差分析

利用2022年1月2日宁蒗M_S 5.5地震序列中1 043次M_L≥1.2（M_c）地震目录，利用公式（1），以100个地震为窗长、1个地震为步长计算该序列b值。计算结果如图 2所示，由图可见：该序列3次M≥4.0余震前，b值出现明显下降变化；4月7日以来，序列b值开始持续下降，4月16日M_S 4.6地震前最大下降幅度达0.2，此次地震后b值持续下降，下降过程中于4月17日再次发生M_S 4.1地震；此后，b值快速回升，4月23日以来再次出现下降，下降过程中发生4月30日M_S 4.2地震，震后下降过程持续1周左右，5月7日以来变化平稳。

利用公式（2）计算b值误差，结果显示平均误差为0.09，可见误差较小，表明b值计算结果可靠。

4 结束语

通过计算分析宁蒗地震序列b值变化特征，发现强余震前b值存在明显下降变化。众多研究指出，b值与区域应力水平呈负相关关系，分析认为，强余震前b值下降变化可能是区域应力水平增加的一种表现。由此可见，序列b值变化也许可作为强余震的预测依据之一。