1 研究背景

古登堡—里克特定律（logN = a - bM）揭示了震级和累积地震次数之间的关系，即地震发生频次的对数随地震震级数呈线性变化。矩震级比例定律解释了地震矩和地震释放的能量之间的关系（Kanamori，1983）。Templeton等（2009）以1984年加利福尼亚M_W 6.2地震为例，提出小型余震在大地震破裂后的分布特点。利用2004年帕克菲尔德M_W 6.0地震研究发现，重复地震序列符合大森定律分布，即主震发生后时间越久，余震发生频率越低。然而，以往研究多倾向于基于规则的水平区域探究地震矩（M_o）—发震间隔（seismic interval，SI）关系，第三维（深度）对于M_o — SI关系的影响作用仍有待研究。

近年来众多研究结果均显示余震持续时间长短不一，日本气象厅（JMA）发现1946年日本南海M_W 8.1地震后6个月内强度不一的余震活动频繁发生。虽然余震强度不大，但可能会引发一些危险性灾害（仲秋，1976）。本文以日本1997—2015年发生的全范围地震活动三维分布为基础，对余震复发时间间隔的分布特点进行规律性统计和分析，并对地震矩与地震重复间隔关系中的各项参数进行研究，从而探索影响余震复发频度的因素。

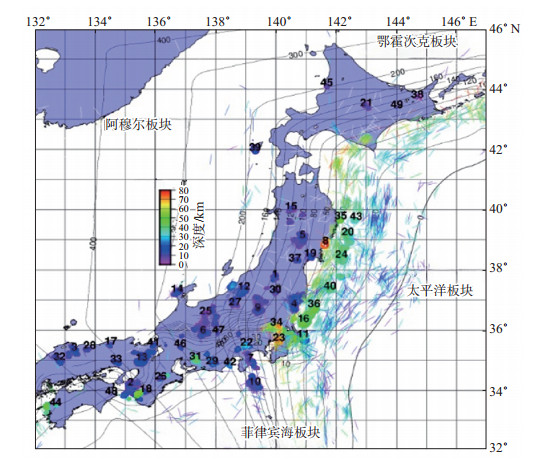
2 研究内容

以日本（132°—147°E，32°—46°N）为研究区域，基于JMA2001地震走时表，选取日本气象厅（JMA）1997年10月1日至2015年2月28日全范围震级地震记录，以三维地震活动统计方法，得到1 842 626个地震的三维分布，采用三维密集地震球法（Ji and Yoshioka, 2021）进行数据处理，得到49个最大震群，称其为密集地震球（seismically dense spheres，下文简称为SDS），震群分布见图 1。其中，大多数地震震级为日本气象厅（JMA）确定使用的矩震级或JMA震级（该值近似于一个地震的矩震级）（Utsu et al，2002）。此外，为详细了解研究区域构造背景，比较了俯冲板块表面等深线（Nakajima and Hasegawa, 2007）以及GCMT项目提供的全球质心矩震源机制解走向。

3 主要震群余震参数及分布特点

计算并给出有明显余震分布的9个震群的余震参数统计结果，见表 1。

（1）SDS3属于陆内震群，深度在10 km以内，余震地震矩最大值约10¹⁶，最小值约为10⁸，相差近8个数量级，余震回归周期约3.25年；SDS8、SDS10位于俯冲界面地震区，其中SDS8深度为67.22 km，余震地震矩最大值近似为10¹⁶，最小值约为10⁹，相差近7个数量级，余震回归周期近似为10.75年；SDS10深度约14 km，余震地震矩最大值为10¹⁶，最小值为10⁹，余震回归周期约为14年。结合余震分布图来看，3个SDS虽深度不一，幅度和余震回归周期也不尽相同，但其振幅均呈幂级数衰减，余震复发时间间隔存在明显的弹性回归分布特点，主震发生后，余震的复发时间间隔逐渐延长，从几分钟到几小时，最后延长至数十天，随后复发间隔趋于稳定，相应的地震震级逐渐衰减至一个稳定的值域范围。

（2）SDS12、SDS14和SDS17三个震群均属于内陆震区，深度均在10 km以内，且相差不大，余震地震矩最大值近似为10¹⁶，其中SDS12、SDS17最小值为10⁹，SDS14最小值为10⁸，余震回归周期均近似为2年。

（3）SDS19、SDS27和SDS38三个震群的深度在5.6—8.5 km的范围内，其中SDS19和SDS38位于俯冲界面地震区，余震地震矩均近似从10¹⁶衰减至10⁸，受深度影响，余震回归周期分别为7.5年、5.3年；SDS27属于陆内震区，余震回归周期约3年，地震矩从10¹⁶衰减至10⁹。3个震群振幅仍符合幂级数衰减规律，余震复发间隔同样从强震发生后几分钟逐渐延至数十天，整体上呈现幂级数衰减趋势。

不同震群的余震回归分布虽然受所在区域和深度影响，在振幅和回归周期上有所不同，但均符合幂级数衰减规律，即修正后的大森定律n(t) = K/(t + c)p（Utsu et al，1995）。余震地震矩振幅取决于K值，而回归周期取决于P值。内陆地震（如SDS3、SDS12、SDS14、SDS17、SDS27）回归周期总体上短于俯冲界面地震（如其他SDS）回归周期，这可能是由于俯冲界面地震P值更小，受俯冲地震楔区域的粘弹性结构影响，其弹性回跳周期更长。

4 结束语

对日本近十几年的地震记录进行分析，发现普通地震的地震矩（M_o）通常与地震复发时间间隔（SI）成正比，地震丛震事件的地震矩率约为10⁴—10⁶；余震复发时间间隔符合弹性回归分布，复发时间间隔逐渐延长，符合大森定律；三维地震断层滑动影响M_o— SI关系中各项参数的变化，且深度在其中具有重要作用。

感谢中国科学院青藏高原研究所超算中心对本研究的大力支持。