0 引言

随着科学技术的不断进步，地震仪器的精密程度越来越高，环境噪声对地震仪器监测能力的影响也越发不容忽视。Peterson（1993）通过研究全球75个地震台站近2 000条地震环境噪声功率谱密度曲线，得出全球高噪声模型（NHNM）和低噪声模型（NLNM），该模型的应用，为衡量全球地震台站环境噪声水平提供了依据。McNamara等（2004）在Peterson（1993）的研究基础上，运用功率谱概率密度函数（Probability Density Function，简称PDF）来分析环境噪声水平。运用PDF方法，在计算过程中不需要去除地震等突发事件记录，也不需要去除外界噪声较小时段数据，可以保证数据的完整性和连续性，从而可更加准确地反映地震环境噪声的时空变化特性。相关研究有：蔡辉腾等（2019）运用PDF方法，利用2014年福建地震台网宽频带地震仪连续观测数据，得出福建省地震台站不同时段的人文噪声水平；颜文华等（2016）提出利用背景噪声互相关提取经验格林函数，分析研究区域背景噪声源的时空特性，并根据地震台阵背景噪声得出甘东南地区噪声来源及其季节变化特性；王俊等（2009）提出通过研究地震台站在0.01 s—20 Hz频带范围内三分向背景噪声特征，了解江苏省数字地震台站的背景噪声情况，以及了解江苏省内地表噪声随区域地形变化的特性；侯颉等（2019a）认为，环境背景噪声在一定程度上限制了地震台站监测能力，不能清晰记录到小于地震台站背景噪声的微小信号；侯颉等（2019b）利用Welch算法，选取北京市28个测震台站不同时段地震连续波形，计算各台站台基噪声功率谱，得出北京市测震台网各地震台站台基噪声背景优势频率；安全等（2021）通过研究内蒙古区域背景噪声，得出山洞台站在低频段受温度和湿度的影响要比地面台小得多。

本文拟通过分析锡林浩特地震台2020年记录波形数据加速度功率谱密度和相应概率密度函数、1—20 Hz频段RMS值，研究该台背景噪声特征，深入了解全年不同时段、不同频段背景噪声对观测数据的影响程度，为该台地震观测数据质量分析及干扰处理提供参考。

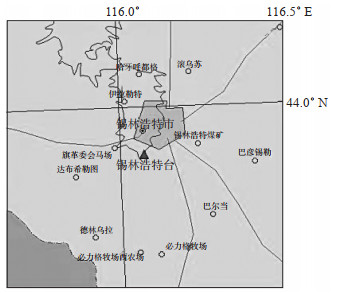
1 台站概况

锡林浩特地区地质构造复杂，属内蒙古弧形构造带东南边缘的三级构造单元，境内主要地质构造可并入弧形构造和新华夏系统构造体系。该区地貌为低山和丘陵，山脉走向呈NEE向，岩性为燕山期中性粒花岗岩，岩石坚硬完整。锡林浩特地震台（下文简称锡林浩特台）地处兴蒙造山带东南部，海拔高程1 020 m，位于人口较密集、交通相对发达的锡林浩特市郊区，近年来随着城市化进程，人类活动产生的噪声影响逐年增多，噪声源多且复杂。台站位置见图 1，基本信息见表 1。

锡林浩特台是内蒙古自治区中西部地区重要的观测台站，担负着本区近震和全球远震监测分析任务，为内蒙古自治区地震局数据分析、地震预报等研究提供重要的基础数据。

2 数据选取

受城市扩张影响，锡林浩特台观测数据质量逐年下滑。2020年1—2月，受疫情防控影响，锡林浩特当地人类活动较少，3—12月人类活动相对频繁，基于当年噪声数据，对比分析人类活动对台站观测数据的影响，为观测数据质量提升提供一定的理论依据。

选取锡林浩特台2020年测震数据，对原始波形进行预处理，采用PDF方法，分析台基噪声特性。采用PDF方法进行计算，不需要排除地震等突发事件及观测系统的瞬态变化、毛刺（如数据记录阶跃、限幅、尖峰、标定）等，因此，拾取的波形数据中含有上述信号，地震台站台基噪声特性图将更加精确。

3 数据分析

功率谱概率密度函数计算步骤如下：①为压制旁瓣效应，平滑傅里叶变换的计算结果，将正弦窗附加在数据序列上，加窗造成的影响在计算傅里叶变换后进行补偿；②计算数据序列的加速度功率谱密度PSD值，并以dB为单位进行展示，以便与全球低噪声模型（NLNM）、全球高噪声模型（NHNM）进行对比分析；③将PSD值进行1/9倍频程光滑，进而得到在对数坐标上均匀分布的PSD；④重复步骤①和③，计算PDF。

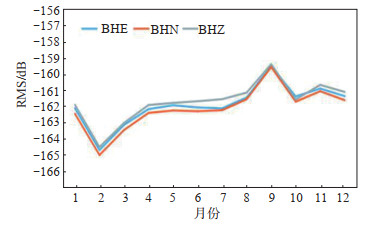
3.1 RMS值三分向月变化特征

选用锡林浩特台2020年1—12月连续波形数据，计算每月连续波形1—20 Hz频段RMS值，绘制三分向RMS平均值月变化折线图，见图 2，可见：三分向RMS值月变化特征基本一致，最大差值在1 dB以内；RMS值随月份不同有一定波动，其中2月数值最低，9月最高，差值达5 dB以上，而其他月份三分向RMS值变化均衡，差值较小。分析认为，2020年2月RMS值较低由春季及疫情防控造成人类活动减少所致，而9月RMS值偏高原因需进一步分析。

3.2 2月和9月垂直向PSD值变化特征

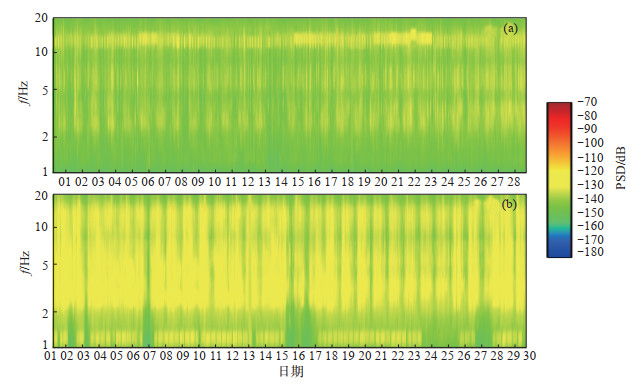
为进一步分析锡林浩特台2020年2月和9月背景噪声变化特征，选取2个月的连续波形数据，计算垂直向1—20 Hz频段PSD值，PSD值随时间的变化见图 3。

2020年2月，锡林浩特台PSD值在1—20 Hz频段数值变化幅度较小，且绝对值较低，由图 3(a)可见：在2—8 Hz和11—16 Hz频段，PSD值以一定规律呈高低交替变化，这种变化与人类昼夜活动规律有关。2020年9月，锡林浩特台PSD值在1—20 Hz频段变化幅度较大，可能由工厂、公路、人类活动等多重因素影响所致。由图 3(b)可见：在0.5—2 Hz和＞19 Hz频段，PSD值偏低；在2—6 Hz频段，PSD值偏高；在2—10 Hz频段，9月1日—16日和28日—30日PSD值呈无规律变化，9月17日—28日则以一定规律呈高低变化；在10—18 Hz频段，PSD值以一定规律呈高低变化。

对比2020年2月和9月锡林浩特台PSD值变化可知，在1—20 Hz频段，9月PSD值明显偏高，最高差值可达约20 dB，主要由这2个月所受人为活动干扰强度不同所致，2月人类活动较平静，而9月则相对活跃。

3.3 PSD平均值逐月变化

选取锡林浩特台2020年测震记录连续波形数据，计算每月PDF最高值对应的PSD平均值，并在0.01—50 Hz频段内绘制其分布图，结果见图 4。

由图 4可见：①在0.01—0.1 Hz频段，水平向PSD值明显高于垂直向，最高差值可达20 dB，可能与该频段水平向PSD值对地倾斜环境变化因素更敏感有关；②在0.1—1 Hz频段，PSD值呈一定季节性变化，各月PSD值在0.25 Hz附近均出现峰值变化，且峰值幅度不同，1月、2月和12月峰值最高，约-130 dB，7月峰值最低，约-138 dB，差值约8 dB；③在1—50 Hz频段，PSD值逐月分布有一定变化，其中：2月PSD值最低，应与春节期间和疫情防控期人类活动减少有关；9月最高，应与该月人类生产、生活等有关；3—12月PSD值在1—1.6 Hz频段出现峰值变化，应与距台站2 km左右的锡林浩特市人类活动影响有关。

4 结论

选用锡林浩特测震台2020年连续观测数据，通过计算加速度功率谱密度、功率谱概率密度及1—20 Hz频段RMS值，分析该台背景噪声变化特征，得到如下结论：

（1）锡林浩特台三分向RMS值逐月变化规律基本一致，2月数值最低，9月最高，其他月份变化均衡。

（2）2月背景噪声偏低主要与春节和疫情防控期人类活动减少有关，9月背景噪声偏高主要与人类生产、生活等因素有关。

（3）在0.01—0.1 Hz频段，水平向PSD值明显高于垂直向，最高差值可达20 dB；在0.1—1 Hz频段，各月PSD值在0.25 Hz附近均有峰值出现，且幅度呈一定季节性变化，应为受到Ⅱ类海洋噪声影响所致；在1—1.6 Hz频段，3—12月PSD值在均有峰值出现，应为距台站2 km左右的锡林浩特市人类活动影响所致。

本研究结果对于认识锡林浩特台背景噪声特征有较大参考意义，可根据背景噪声变化特征分析远震、近震波形特征，提高观测数据质量。