预测地震需依据地震孕育过程中导致的各种宏观和微观异常,即地震前兆(钱家栋,2010)。长期的地电阻率观测表明,在大震前记录的显著中短期异常多以趋势性下降、破年变为主,是一种被证实的有效的地震前兆(钱家栋等,1985)。然而,并非所有变化都与地震孕育过程相关,其中地电阻率年变化对地震监测预报造成较大干扰(方炜等,2019)。多项研究(赵和云等,1985;田山等,2000;沈红会等,2020)发现,地下水位、降雨、地温、气温、气压等均与地电阻率年变化相关。数值模拟研究(钱家栋等,1988;毛先进等,2003;解滔等,2020)表明,台址基岩电性断面、水文地质条件、观测系统装置参数等是地电阻率年变化的基本成因。对固定观测的地电阻率台站而言,影响系数将地电阻率的相对变化与台址下电性结构变化相联系,以此对地电阻率年变进行物理机制解释(杨明芝等,1986;Park et al,1991)。
银川望洪地电台(以下简称银川台)电阻率三测道整体存在“夏高冬低”的“反向年变”,年变幅度约为1%。本文通过流体观测井静水位和气象观测数据与地电阻率数据的相关分析,明确了影响该台年变的主要因素,结合影响系数理论和地电阻率年变化数值模拟,尝试对各影响因素物理机理进行分析。
1 台站概况及观测资料介绍银川台地电阻率观测场地位于银川市永宁县望洪镇农丰三队,距银川市区28 km,海拔高程1 087 m。该场地在地貌上属黄河二级阶地,地表为黄河冲积物,岩性组成为细砂、砂粘土等。观测区位于农田,周围地势平坦开阔,最大高差1.1 m;测区以西150 m为汉延渠,以东200 m为石中高速公路,交通、电力、通信便利。
在区域地质构造上,测区地处银川断陷盆地(图 1)。该盆地北起石嘴山以北正谊关断裂,南以青铜峡为界,东以鄂尔多斯盆地西缘为界,西以贺兰山东麓断裂为界(周佃刚,2014)。银川盆地的沉积和演化自西向东依次受到贺兰山东麓断裂、芦花台隐伏断裂、银川隐伏断裂及黄河断裂4条正断层控制,新生代沉积巨厚,是一个受断裂活动控制、构造运动强烈、地震频发的新构造单元(雷启云,2016),1739年平罗8级大震即发生于此。

|
图 1 银川台周边地质构造分布 Fig.1 Distribution of geological structures around the Yinchuan Seismic Station |
观测区地属中温带干旱气候区,大陆性气候特征明显。地表水和地下水主要受大气降水、农田灌溉补给。年平均气温8.7 ℃,多年平均降水量为201.4 mm,年平均蒸发量为1 470.1 mm。
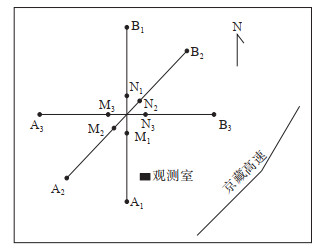
银川台采用ZD8M地电仪进行地电阻率观测,观测系统设置NS、EW、N45°E三个测道,电极布设采用对称四极装置,其中3测道供电极距AB均为1 000 m,测量极距MN均为200 m,电极埋深10 m(图 2)。
|
图 2 电极布设 Fig.2 Electrode layout diagram |
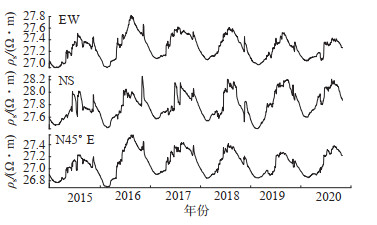
银川台地电阻率年变幅约为1.5%。通常认为,地下介质含水率越高,地电阻率观测值应当越小(Lu et al,2004),但该台地电阻率观测曲线则相反,春季后,随着温度升高,冻土层逐渐融化,浅层介质含水率增加,随后进入灌溉期(5—9月),浅层介质含水率进一步上升,三测向地电阻率呈上升变化,在灌溉末期地电阻率处于年变高值状态,具有典型的“夏高冬低”的“反向年变”形态(图 3)。
|
图 3 地电阻率日均值曲线 Fig.3 The daily mean curve of ground resistivity |
研究表明,在探测深度偏浅时,地电阻率年变受诸多气象因素(气温、气压、降雨、水位等)影响(张国苓等,2016;饶文等,2021)。为定性分析地电阻率年变影响因素,结合银川台流体观测井静水位和气象辅助观测数据,利用相关系数法确定其主要影响因素。
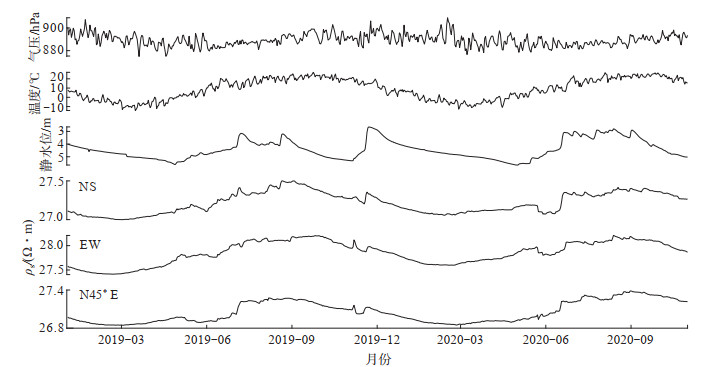
银川台静水位观测井建于2018年5月,同年11月正式观测,为保证数据的可靠性,选取2019年1月1日至2020年10月31日的静水位日均值,与同期地电阻率、气温、气压时序曲线进行对比,结果见图 4,可见地电阻率年周期变化与静水位变化呈负相关,与气温呈正相关,与气压呈正相关。
|
图 4 气压、温度、静水位与地电阻率同期对比 Fig.4 Simultaneous comparison of air pressure, temperature, static water level, and ground resistivity observations |
为了消除地电阻率测值中的随机干扰因素,突出地电阻率的周期变化和长期变化趋势,采用气压、温度、静水位和地电阻率的月均值数据,计算地电阻率与气压、温度、静水位等影响因素之间的相关系数r,计算公式如下
| $ r = \frac{{\sum\limits_i {\left({{x_i} - \bar x} \right)} \left({{y_i} - \bar y} \right)}}{{\sqrt {\sum\limits_i {{{\left({{x_i} - \bar x} \right)}^2}} \times \sum\limits_i {{{\left({{y_i} - \bar y} \right)}^2}} } }} $ | (1) |
式中,xi为地电阻率观测值,yi为相应影响因素观测值。
根据式(1)分别计算得到银川地电阻率三测向与水位、气温、气压的相关系数r值,结果见表 1。通过查询相关系数显著性检验表可知,除气压与地电阻率测值呈显著不相关外,其他2项均与地电阻率测值具有较好的相关性。采用多元线性回归方法,基于相关系数得到地电阻率拟合值,并计算其与实测值的残差值,以期消除地电阻率年变,提取地球物理异常。
| 表 1 地电阻率与气压、气温、静水位的相关系数 Table 1 Correlation coefficients of earth resistivity with air pressure, air temperature, and static water level |
线性回归方程如下
| $ y = {a_0} + {b_1}{x_1} + {b_x}{x_2} $ | (2) |
式中,y为地电阻率实测值,x1为温度实测值,x2为静水位实测值,a0为常数项,b1为地电阻率对温度的回归系数,b2为地电阻率对静水位的回归系数。选取同时段观测数据,利用最小二乘法,求得地电阻率与温度和静水位的系数值,得到地电阻率三测向对二者的线性回归方程,公式如下
| $ \begin{array}{l} {y_{{\rm{NS}}}} = 27.2306 + 0.011{x_1} - 0.0274{x_2}\\ {y_{{\rm{EW}}}} = 27.7094 + 0.0184{x_1} - 0.0045{x_2}\\ {y_{{\rm{N}}{{45}^ \circ }{\rm{E}}}} = 27.1971 + 0.0113{x_1} - 0.0546{x_2} \end{array} $ | (3) |
将温度和静水位同期观测数据代入式(3)中,得出该时段地电阻率拟合值,计算实测值与拟合值的差值,所得残差曲线即为消除温度和静水位年变影响的地电阻率观测曲线,见图 5,可见银川地电阻率测值基本处于正常变化范围,但仍存在局部畸变,可能与台址区农田灌溉有关,需进一步研究。

|
图 5 年变消除后的地电阻率残差曲线 Fig.5 Residual ground resistivity curves after eliminating annual variation |
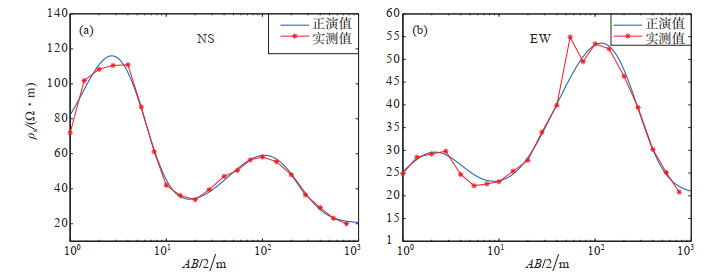
银川台地下介质电测深结果显示,NS、EW向电性结构差别不大,测区地下介质较均匀。基于水平层状介质理论,应用试错法来确定研究区地下介质电性结构参数(赵和云等,1986)。依据银川台地电场测区地质资料,假定一组电性结构参数(电阻率、层厚),通过滤波器算法计算不同观测极距下的地电阻率值,并与电测深观测值对比,不断修正电性结构参数,直至二者高度吻合,则表明该组参数满足台址区地电阻率物理建模计算的要求。将银川台台址区地下电性结构设为5层,各层参数设置见表 2,对不同供电极距下NS、EW向测值进行正演模拟,与实测曲线进行对比,结果见图 6,可见假定的电性结构参数满足银川台地电阻率物理建模计算的要求。
| 表 2 台址区地下电性结构参数设置 Table 2 Parameter setting of underground electrical structure in the site area |
|
图 6 台址区电性结构和电测深曲线实测值和正演值 Fig.6 The observed and simulated values of the electrical structure and electrical bathymetry curves in the site area |
上述相关性分析结果表明,银川台地电阻率年变与浅水位和季节性温度变化相关。一般认为,温度和表层水位的变化不能直接引起地电阻率变化,而是通过对台址表层介质的影响,导致电性结构剖面发生改变,从而引起地电阻率测值的变化。因此,地电台址下介质的电性结构剖面是变化的,特别是地表介质电性,随季节变化,受气象因素(气温、气压、降水、地温)和人为因素(灌溉、抽水)的影响而发生较大变化(金安忠,1981)。
根据扩展的阿契定律可知,温度升高,表层土壤中导电粒子活跃度增加,表层真电阻率减小。因此,可以假定测区表层介质真电阻率受气温和浅水位影响的变化规律服从正弦函数,即夏季(灌溉期)温度和水位升高,表层介质真电阻率降低,而冬季表层真电阻率则增大。因地表薄层效应影响一般仅局限在地下2 m以内,根据银川台台址下介质的电性结构剖面设置(表 2),确定NS、EW测道地表浅层(层1、层2)电阻率随时间的变化,即
| $ \rho _i^ * = {\rho _i}(1 + 0.8\sin (\omega t)) $ | (4) |
式中,ρi*为随时间变化的第i电性结构层电阻率,ρi为第i层电阻率,ω= 2π/T,T为1年。
将表 2所示组1、组2中层1、层2的数值代入公式(4),计算得到NS、EW测道层1、层2的模拟数值,结果见表 3。
| 表 3 台址区地下2层电性结构参数 Table 3 2-layered underground electrical structure parameters in the site area |
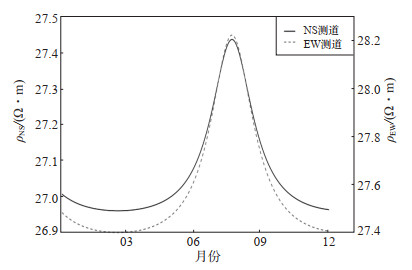
基于表 3,对银川台地电阻率NS、EW测向2019年度数值进行正演模拟,分析地电阻率年变模拟曲线变化特征,结果见图 7,可见地电阻率模拟曲线呈“夏高冬低”的“反向年变”形态,年变幅分别为1.7%和2%,与2测道数值年变形态基本一致,说明薄层效应对银川地电阻率年变形态影响明显。
|
图 7 地电阻率年变模拟 Fig.7 Simulation of ground resistivity annual variation |
将地电阻率测区按N层水平层状结构划分为N块区域,每一层介质电阻率为ρi,其中i = 1,2,…,N。在测区电性结构确定、观测装置确定的情况下,地电阻率观测值ρa是各层介质电阻率ρi的函数(解滔等,2015),公式如下
| $ {\rm{d}}\left({\ln {\rho _{\rm{a}}}} \right) = \sum\limits_{i = 1}^N {\frac{{\partial \ln {\rho _{\rm{a}}}}}{{\partial \ln {\rho _i}}}} {\rm{d}}\left({\ln {\rho _i}} \right) $ | (5) |
多数情况下,各层介质电阻率在一定时间内的相对变化较小,Δρi/ρi<<1,因此将式(5)进行Taylor级数展开,二阶及高阶项远远小于一阶,可忽略不计。地电阻率的相对变化可以简单表示为各分区介质电阻率相对变化的加权和,即
| $ \frac{{\Delta {\rho _{\rm{a}}}}}{{{\rho _{\rm{a}}}}} = \sum\limits_{i = 1}^N {{S_i}} \frac{{\Delta {\rho _i}}}{{{\rho _i}}} $ | (6) |
式中,N表示测点下方均匀介质的分层总数,i为介质分层的序号,Δρi/ρi表示第i层介质(真)电阻率的相对变化量,Δρa/ρa表示地表地电阻率装置系统所测相对变化量,比例系数Si为地电阻率影响系数,则有
| $ {S_i} = \frac{{\partial \ln {\rho _{\rm{a}}}}}{{\partial \ln {\rho _i}}} = \frac{{{\rho _i}}}{{{\rho _{\rm{a}}}}}\frac{{\partial {\rho _{\rm{a}}}}}{{\partial {\rho _i}}} $ | (7) |
同时,影响系数Si满足如下关系
| $ \sum\limits_{i = 1}^N {{S_i}} = 1 $ | (8) |
采用解析表达式和对称四极装置汉克尔滤波器算法,按照表 2所示层状电性结构,在水平层状均匀模型下计算地电断面各层介质地电阻率变化对地电阻率的影响系数,NS测向和EW测向电性结构的影响系数随观测极距的变化见图 8,可见在供电极距AB = 1 000 m时,测区地下介质层1、层2、层3影响系数S1、S2、S3均为负值。

|
图 8 台址区地下电性结构影响系数(实线表示正值,虚线表示负值) Fig.8 Influence coefficients of underground electrical structure in the site area (solid lines indicate positive values, dotted lines indicate negative values) |
用ρNS和ρEW分别表示NS、EW测向地电阻率地表观测值,当AB = 1 000 m、MN = 200 m时,银川台地电阻率ΔρNS/ρNS和ΔρEW/ρEW相对变化值分别为
| $ \frac{{\Delta {\rho _{{\rm{Ns}}}}}}{{{\rho _{{\rm{NS}}}}}} = - 0.0027\frac{{\Delta {\rho _1}}}{{{\rho _1}}} - 0.000583\frac{{\Delta {\rho _2}}}{{{\rho _2}}} - 0.1280\frac{{\Delta {\rho _3}}}{{{\rho _3}}} + 0.2420\frac{{\Delta {\rho _4}}}{{{\rho _4}}} + 0.8855\frac{{\Delta {\rho _5}}}{{{\rho _5}}} $ | (9) |
| $ \frac{{\Delta {\rho _{{\rm{EW}}}}}}{{{\rho _{{\rm{EW}}}}}} = - 0.0065\frac{{\Delta {\rho _1}}}{{{\rho _1}}} - 0.000139\frac{{\Delta {\rho _2}}}{{{\rho _2}}} - 0.1049\frac{{\Delta {\rho _3}}}{{{\rho _3}}} + 0.3051\frac{{\Delta {\rho _4}}}{{{\rho _4}}} + 0.8033\frac{{\Delta {\rho _5}}}{{{\rho _5}}} $ | (10) |
据式(7)计算得到银川台地电阻率NS、EW测向表层介质影响系数分别为-0.131和-0.111,表明地表介质电阻率对该台地电阻率观测值变化幅度影响不大,即地电阻率年变幅较小。影响系数为负表明,随着地表介质地电阻率的减小,地电阻率观测值上升,即温度升高,冻土层逐渐融化,且夏季灌溉期来临,表层潜水位埋深减小,地表介质地电阻率减小,地电阻率观测值上升,与实际观测资料相符。
5 结论通过对银川台地电阻率年变化影响因素及其机理分析,得出以下结论:
(1)根据相关分析和多元线性回归理论,明确了银川台地电阻率“夏高冬低”的年变形态受温度和水位的影响较大,受气压影响不明显。
(2)通过改变电性结构参数,模拟了银川台地电阻率年变形态,结果表明,银川地电阻率“夏高冬低”的年变形态主要由地表薄层介质电阻率的季节变化引起,薄层效应对年变影响较大。
(3)基于银川台电测深反演的层状介质结果,通过影响系数理论分析了地表介质电阻率对地电阻率年变化的影响。表层介质对地电阻率的影响系数为负,表明银川台地电阻率观测受地表浅层介质电阻率夏低冬高的季节性变动影响时,应表现夏高冬低的年变,与实际观测资料相符。
方炜, 张国强. 地电阻率年变化特征及机理解释[J]. 国际地震动态, 2019(8): 9. DOI:10.3969/j.issn.0253-4975.2019.08.007 |
金安忠. 地电阻率正常变化与电剖面的关系[J]. 地震学报, 1981, 3(4): 421-428. |
雷启云. 青藏高原东北缘弧形构造带的扩展与华北西缘银川盆地的演化[D]. 北京: 中国地震局地质研究所, 2016.
|
毛先进, 李志祥, 杨玲英. 台址下表层介质电阻率变化对视电阻率观测值影响特征的初步研究[J]. 地震研究, 2003, 26(4): 338-342. DOI:10.3969/j.issn.1000-0666.2003.04.007 |
钱家栋, 陈有发, 金安忠. 地电阻率法在地震预报中的应用[M]. 北京: 地震出版社, 1985.
|
钱家栋, 赵和云. 地电阻率的数值模拟和多极距观测系统[J]. 地震学报, 1988, 10(1): 77-89. |
钱家栋. 地震电磁学理论基础与观测技术(试用本)[M]. 北京: 地震出版社, 2010: 93-105.
|
饶文, 刘海洋, 张治广, 等. 柯坪地电阻率台年变特征及成因分析[J]. 地震地磁观测与研究, 2021, 42(1): 61-68. DOI:10.3969/j.issn.1003-3246.2021.01.009 |
沈红会, 叶碧文, 孙春仙, 等. 地电阻率与水位关系的机理分析[J]. 地震, 2020, 40(4): 183-190. |
田山, 郑文俊, 关华平, 等. 地电阻率年变化与气象因素及水位的关系[J]. 地震, 2000, 20(4): 45-49. |
解滔, 卢军. 地电阻率三维影响系数及其应用[J]. 地震地质, 2015, 37(4): 1125-1135. DOI:10.3969/j.issn.0253-4967.2015.04.015 |
解滔, 卢军. 含裂隙介质中的视电阻率各向异性变化[J]. 地球物理学报, 2020, 63(4): 1675-1694. |
杨明芝, 张文孝, 赵和云. 关于层状介质视电阻率响应系数的研究[J]. 西北地震学报, 1986, 6(2): 27-38. |
张国苓, 乔子云, 贾立峰, 等. 河北昌黎地电阻率频谱特征分析[J]. 地震地磁观测与研究, 2016, 37(1): 57-62. |
赵和云, 张文孝. 银川台地电阻率趋势变化及年变的分析[J]. 地震, 1985, 5(1): 32-38. |
赵和云, 钱家栋. 地电阻率观测中的地表薄层影响与数学模拟[J]. 地震, 1986, 6(5): 37-41. |
周佃刚. 贺兰山-银川盆地上地壳电性结构研究[D]. 成都: 成都理工大学, 2014.
|
Lu J, Xue S Z, Qian F Y, et al. Unexpected changes in resistivity monitoring for earthquakes of the Longmen Shan in Sichuan, China, with a fixed Schlumberger sounding array[J]. Physics of the Earth and Planetary Interiors, 2004, 145(1/4): 87-97. |
Park S K, Van G P. Inversion of pole-pole data for 3-D resistivity structure beneath arrays of electrodes[J]. Geophysics, 1991, 56(7): 951-960. |
 2022, Vol. 43
2022, Vol. 43

