2) 中国合肥 230031 安徽省地震局;
3) 中国南京 210014 江苏省地震局;
4) 中国邢台 054000 河北红山巨厚沉积与地震灾害国家野外科学观测研究站;
5) 中国廊坊 065201 华北科技学院计算机学院
2) Anhui Earthquake Agency, Hefei 230031, China;
3) Jiangsu Earthquake Agency, Nanjing 210014, China;
4) National Field Scientific Observation and Research Station for Huge Thick Sediments and Seismic Disasters in Hongshan, Xingtai 054000, China;
5) School of Computer, North China Institute of Science & Technology, Langfang 065201, China
地磁场是地球固有的基本特性,地磁数据的变化规律对于震磁关系研究具有重要意义。然而,伴随着工厂、铁路、高压直流输电线路等现代化基础设施建设,附近的地磁观测仪器日益受到严重影响,地磁观测数据质量下降,相关研究进展被制约。现有地磁场观测数据中的干扰事件种类繁杂,如仪器故障、基建工程或人为干扰等(李正媛等,2016),其表现形态多样,如短时突跳、尖峰、台阶等。通常情况下,同一台站地磁观测设备受同一类型干扰事件的影响,也会因为干扰事件的强度、距离等不同而表现出不同形态。为了提高地磁观测数据质量,除加强环境保护与仪器的抗干扰技术外,加强干扰事件识别技术研究,剔除干扰事件对数据的影响也是一种重要手段(樊俊屹等,2021)。本研究目标就是自动、快速、准确地判断一段给定的地磁场观测数据中是否包含干扰事件的影响,为下一步剔除干扰影响做准备。
目前,地磁台站通用的干扰事件识别方法是,选择一个未受干扰的近距离参考台站的观测仪器,与目标台站观测仪器对应测项分量的观测数据做差值,通过查看波形变化,结合专家经验判断是否为干扰事件,开展干扰落实工作,并向学科管理部门提交干扰落实报告(应允翔等,2021)。然而,这种半人工干扰事件识别方法不仅耗时耗力、效率低下,而且还伴随着人为误差,随着仪器数量的增多,观测数据规模激增,这种方法已不再适用。为了能够自动、快速、准确地识别干扰事件,提高地磁观测数据质量,研究人员提出基于滤波和统计学的干扰事件识别方法。如:王立辉等(2020)提出一种基于CEEMD滤波和IMF分类的多尺度干扰事件检测方法;杨学慧等(2020)利用一阶差分、线性插值和参考分量斜率反算等方法识别高压直流输电干扰事件;廖绍欢等(2021)利用一阶差分方法识别并去除地磁观测数据中的尖峰干扰;李章等(2021)依靠邻近台站地磁数据的加权拟合,重构因干扰事件而缺失的数据。这些干扰事件识别方法使得干扰事件检测和识别的效率显著提高,但这些方法一般只针对某种典型的干扰事件,通常还要依靠专家经验,自动化程度不高、泛化能力不足。因此,有必要研究一种泛化能力强,兼顾精度和效率的干扰事件识别方法。
随着计算机技术的进步,机器学习(Machine Learning,ML)方法的出现为地磁干扰事件识别提供了一种新的思路。相关研究有:王静等(2020)通过离散Gabor变换提取磁暴的特征值,并利用SVM算法识别正常数据和磁暴数据;刘军等(2020)采用基于混沌蚁群优化的小波阈值法去除地磁干扰噪声;程文凯等(2021)基于XGBoost方法,对因严重干扰而造成的缺失数据进行重构。相比于传统的滤波和统计学方法,基于机器学习的干扰事件识别方法不需要过多的人为干预,干扰事件识别的自动化程度有了明显提高。但是,机器学习方法严重依赖于特征选择(张帆等,2021),而地磁观测数据作为一种时间序列数据,难以准确刻画其数据特征,加之干扰事件持续时间不同,形态差异较大,导致基于机器学习的干扰事件识别方法泛化能力和识别精度仍然有限。
深度学习(Deep Learning,DL)方法往往对原始数据的人为加工较少,从而保留了其中大部分原始信息,不需要人为干预,使用多层神经网络自动提取数据特征,在图像分类、人脸识别、音频检索、时间序列异常检测与识别等领域取得巨大成功(周飞燕等,2017;Purwins et al,2019;Qian et al,2020;Ku et al,2021;Yin et al,2022)。近年来,卷积神经网络(Convolutional Neural Networks,CNN)等深度学习方法被应用在地震断层识别、地震速度建模、地震事件预测等领域(Geng et al,2019;韩明亮等,2021;杨晶等,2022)。例如,Xu等(2020)将包含5个卷积层的CNN用于地磁场异常信号识别;王军等(2021)应用6层CNN网络识别井水位观测数据中的抽水异常识别;Liu等(2022)应用MLP、SVN和CNN识别地磁场干扰事件。此外,Vaswani等(2017)提出基于自注意力(Self Attention,SA)机制的Transformer模型,通过对重点区域增加更多的注意力,从而提取样本的显著判别模式特征,并且具有参数少、训练速度快、效果好等特点,在自然语言处理(Natural Language Processing,NLP)等领域被广泛应用。近来,Transformer也衍生出多个变种(Wang et al,2022),大量实验结果表明注意力机制具有较好的泛化能力。
基于此,文中将卷积神经网络和自注意力机制深度学习方法引入地磁场观测数据干扰事件识别领域,利用深度学习方法自动提取干扰事件特征,从而实现地磁场观测数据干扰事件自动、快速和准确分类识别,开展了对比实验以评估该算法的有效性和稳定性。
1 干扰事件统计分析及样本制作地磁观测分为地磁相对观测和地磁绝对观测,在地磁相对观测中,地磁观测仪器通常产出多个测项分量数据,如垂直分量Z、水平分量H、磁偏角D等。已有研究人员从原理上开展了不同类型干扰对不同测项分量影响的理论分析(鲍海英等,2020),本研究从数据科学思维方法出发,通过对大量干扰事件样本的自动学习,提取干扰事件对地磁正常观测数据影响的内在特征,进而实现对干扰事件的识别。
因此,对国家地磁台网中心记录的地磁观测数据干扰事件统计发现,2000—2019年共记录30种干扰事件类别、360多万条干扰事件处理记录。海量地磁场干扰事件处理记录,为了解各类地磁干扰事件的数据特征打下了基础,也对应用深度学习技术、准确识别地磁场干扰事件提供了丰富的样本数据。
1.1 干扰事件统计分析对2000年1月1日至2019年12月31日地磁场干扰事件处理记录进行统计,结果见表 1,发现地磁场观测仪器Z(3123)、H(3124)、D(3125)3个测项分量受影响记录数量最多,分别占总数的45.75%、21.58%和20.99%。
| 表 1 2000年1月1日至2019年12月31日干扰事件处理记录数量统计 Table 1 Statistical results of interference eventrecords from January 1, 2000, to December 31, 2019 |
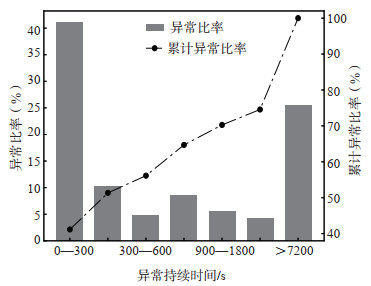
Z分量处理记录数占比较大,因此选择Z分量初步探索干扰事件深度学习识别方法研究。统计发现,造成Z分量影响的各类干扰事件中,24类干扰事件的处理记录数量超过100个,其中3类干扰事件数量占比大于10%,分别是高压直流输电影响、原因不明和基建工程影响事件,占比分别为28.17%、13.45%和11.25%,见表 2。由于干扰事件持续时间通常不同,对表 2列出的地磁观测仪器Z分量记录的干扰事件持续时间进行统计,结果见图 1,可见持续时间小于300 s的干扰事件数量约占总干扰事件数量的40%,持续时间小于7 200 s的干扰事件数量占比为74.56%,大于总干扰事件数量的2/3。鉴于深度学习网络输入的时间序列长度受限,因此选择2012年1月1日到2014年12月31日持续时间在2小时内的Z分量干扰事件数据和原始观测数据,制作干扰事件样本和正常样本,探索基于深度学习技术的地磁场干扰事件识别方法的有效性。
| 表 2 变化记录垂直分量记录的干扰事件占比统计 Table 2 Statistics on the proportion of disturbance events recorded by the vertical component of the change record |
|
图 1 垂直分量记录的干扰事件的分时段比率 Fig.1 The time ratio of disturbance events recorded by the vertical component of change record by time period |
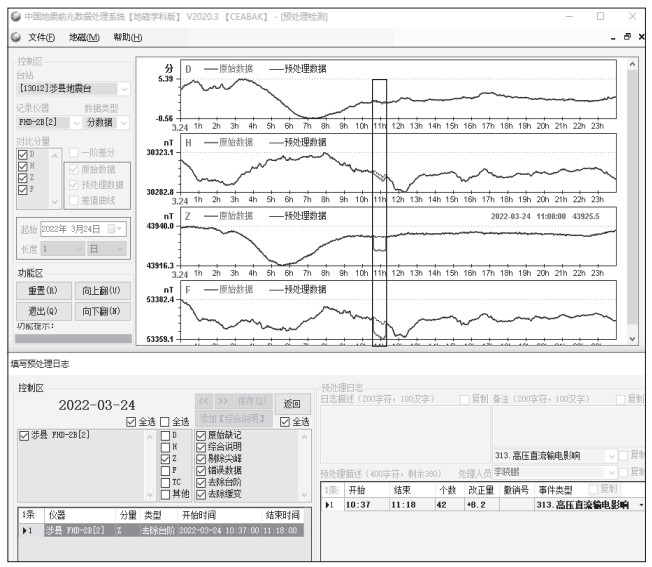
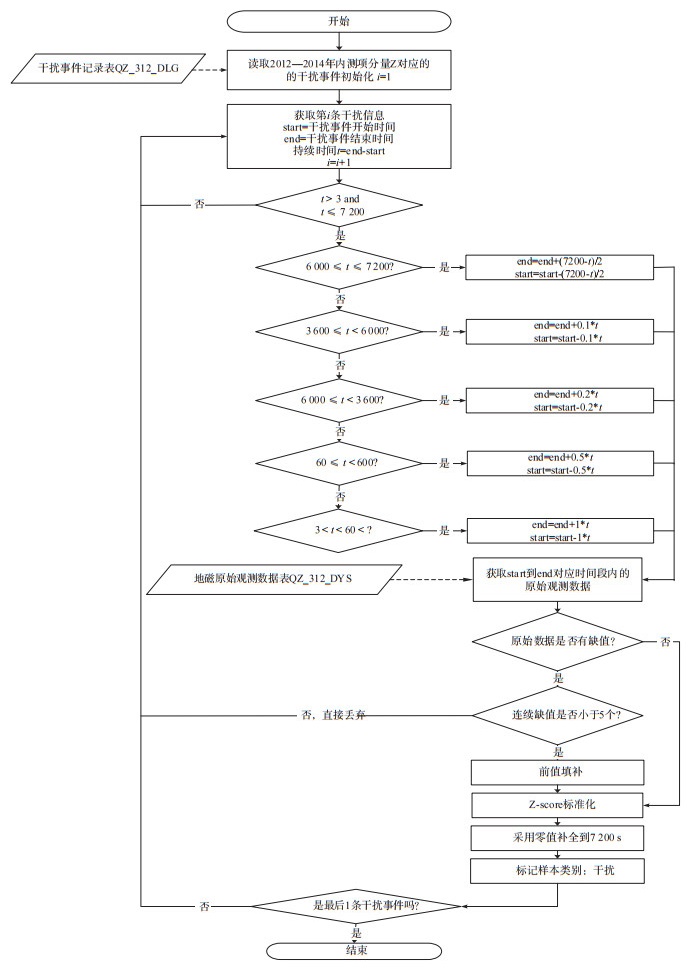
本研究的目的是,期望利用深度学习技术,准确、高效、自动地判断一段给定地磁观测仪器变化记录垂直分量的原始观测时间序列数据是干扰事件样本还是正常观测数据样本(即不包含任何干扰事件),为下一步自动矫正受干扰的数据奠定基础。因此,根据国家地磁台网中心记录的干扰事件起止时间,查找原始地磁观测数据,制作干扰事件样本数据集。由于系统中仅记录了干扰事件的开始和结束时间,若以此起止时间截取原始观测数据,难以完整展现干扰事件的形态变化,不利于识别干扰。如图 2所示,某一高压直流输电干扰事件在观测仪器的Z分量原始数据曲线中表现为一个台阶,若按照日志中记录的开始和结束时间直接截取原始数据制作样本,则样本数据可能近似表现为一条直线,而不是一个台阶。因此,为了提高地磁场干扰事件识别的准确率,在制作干扰事件样本时,尽量让单个样本包含干扰事件的完整变化形态。依据国家地磁台网中心记录的干扰事件持续时间,将样本开始时间和结束时间分别向前、向后延长一段时间。干扰事件样本数据集的制作流程见图 3,具体制作步骤如下:
|
图 2 高压直流输电干扰事件对原始观测数据的影响及处理记录 Fig.2 Influence of HVDC on original observation data and its processing records |
|
图 3 干扰事件样本制作流程 Fig.3 Flow chart of making interference events sample |
(1)读取中国地震台网地磁场干扰事件记录表内2012—2014年垂直分量Z记录的干扰事件信息,每一条干扰事件信息包括事件的开始时间、结束时间、影响的测项分量和干扰事件类型等信息(图 2下半部分)。
(2)从步骤(1)中顺序获取每一条干扰事件,若3 s<干扰事件持续时间≤7 200 s,则进入步骤(3),否则忽略该干扰事件。
(3)按规则向前、向后扩展干扰事件样本的起止时间,以便完整体现干扰事件的形态特征。基本原则是,干扰事件持续时间越短,扩展的时间就相对越长。重新计算干扰事件的开始时间和结束时间。假设干扰事件持续时间为t秒,扩展规则如下:当3<t<60时,干扰事件序列前后各弥补t长度的原始数据;当60≤t<600时,干扰事件序列前后各弥补0.5t长度的原始数据;当600≤t<6 000时,干扰事件序列前后各弥补0.25t长度的原始数据;当6 000≤t≤7 200时,干扰事件序列直接补全7 200 s的数据。选定起止时间后,从国家地磁台网中心原始观测数据表中获取新对应的原始观测时间序列数据。
(4)判断原始观测时间序列数据中空值数是否超过5个。若超过5个,则舍弃本条数据,转步骤(2)处理下一条干扰事件,否则使用前值替换空值。对本条原始数据标准化。
(5)判断干扰事件数据持续时间是否小于7 200 s,若小于7 200 s则使用零值补全。
(6)将该样本标记为干扰事件样本,并追加到干扰事件样本库中。
(7)判断干扰事件是否为最后一条干扰信息,若“是”则结束,否则重复步骤(2)至步骤(7),制作下一个干扰事件样本。
正常样本的制作流程及其时间扩展规则和缺值处理方法与干扰事件样本类似,不同之处在于,正常样本的开始时间和持续时间需要随机生成,且保证该时段内无干扰事件发生。
根据上述样本制作流程(图 3),共制作51 357个地磁场干扰事件样本,为保证样本均衡及模型的泛化能力,同样生成51 357个正常样本,样本数量总计102 714个。
为了提高模型泛化能力,首先将102 714个样本随机打乱,并按照8:1:1的比例划分训练集、验证集和测试集,即训练集占样本总数的80%,共82 171条数据,验证集占样本总数的10%,共10 271条数据,测试集占样本总数的10%,共10 272条数据。
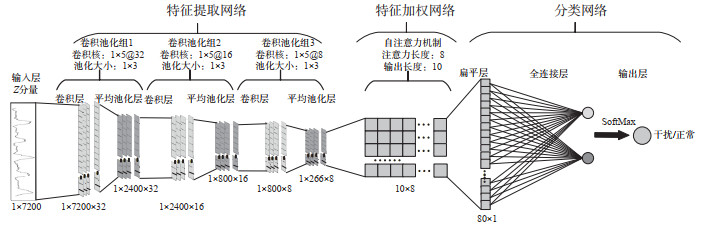
2 干扰事件识别模型利用地磁场原始观测数据,基于卷积神经网络和自注意力机制搭建干扰事件识别深度学习模型,用于自动提取地磁场观测数据中各类干扰事件特征,并实现干扰事件的识别分类。模型网络结构由3个子网络构成:特征提取网络、特征加权网络和分类网络,具体结构见图 4。
|
图 4 基于深度学习的地磁场干扰事件识别模型 Fig.4 The recognition model forgeomagnetic field disturbance eventsbased on deep learning |
特征提取网络由卷积神经网络实现,包含3组卷积池化层,每组各包含一个卷积层和一个池化层。目前,卷积神经网络(Krizhevsky et al,2012)广泛应用于时间序列分类(Qian et al,2020)、地震事件分类(Ku et al,2021)、地震事件定位(Perol et al,2018)等领域,并取得了较好的效果。特征提取网络主要是利用卷积层提取原始地磁观测数据中的高维、非线性特征,并通过使用平均池化层进行降维。单个卷积层可以提取输入数据的一些低级特征,多个卷积层的堆叠可以从低级特征中迭代出更多、更复杂的特征。考虑到一维时间序列数据内在特征不如二维图像数据特征复杂,文中使用3组卷积池化层,3个卷积层对应的卷积核个数分别为32、16和8,卷积核大小均为1×3,卷积步长为1。假设输入长度为n的地磁场变化记录垂直分量一维时间序列向量为X = [x1, x2, …, xn],Wk为卷积层的第k个卷积核的权重,则经过卷积后的输出X′为
| $ X^{\prime}=f\left(W_k * X+b\right) $ | (1) |
式中,*为卷积运算,b为偏置,f为激活函数。以第一层卷积为例,输入层n = 7 200,k为32,卷积核Wk大小为1×3,其输出为1×7 200×32的特征矩阵。
池化层可以有效降低数据维度,从而减少训练参数。使用池化层不仅可以加快计算速度,而且有利于防止过拟合。本实验池化窗口大小均为1×3,池化步长为3。假设池化层的输入为上一层卷积之后的特征向量X′ = [x0′,x1′,…,xm′ ],则池化过程可表示为
| $ \begin{aligned} &y_i=\operatorname{Avg}-\operatorname{pooling}\left(\left[x_{i \cdot t}^{\prime}, \quad x_{i \cdot t+r}^{\prime}\right]\right) \\ &r \in[2, \quad p], \quad p \leqslant m, \quad i \leqslant(m-p) / t \end{aligned} $ | (2) |
式中,Avg-pooling表示平均池化函数,m表示特征向量的长度,t表示池化步长,r表示池化窗口大小。以第一个池化层为例,其输入是第一层卷积神经网络的输出,因此m = 7 200,池化步长t = 3,池化窗口大小为1×3,池化后的输出为32个1×2 400特征向量。经3组卷积池化操作后,特征提取网络的输出为8个1×266的特征向量。
2.2 特征加权网络特征加权网络主要由自注意力机制组成。作为注意力机制的变种(Vaswani et al,2017;Ramachandran et al,2019),自注意力机制可以从大量输入数据中自动筛选并聚焦到少量重要信息上,忽略大多不重要的信息,擅长捕捉数据中蕴含的长期依赖关系。文中针对卷积神经网络提取多个特征向量,利用自注意力机制进一步提取其中的重要信息,进而放大这些需要注意部分的特征,提高模型分类精度。自注意力模块的核心是自注意力机制,模块的输入为特征提取网络输出的多个特征向量。对于多个特征向量Y ∈ RT×E(E为特征向量个数,T为单个特征向量长度),其注意力得分的计算过程如下
| $ \text { Attention }=\operatorname{Soft} \max \left(V \tanh \left(U Y^T\right)\right) $ | (3) |
| $ A-\text { score }=\text { Attention } \cdot Y $ | (4) |
其中,V∈RF×D与U∈RD×E为自注意力机制的权值矩阵,F表示输出长度,D为注意力长度,E为特征向量个数,·表示点积。利用公式(3)得到的注意力权重与每个特征向量相乘,即得到每个特征向量的注意力得分A - score。本实验规定了注意力长度D为8,输出长度F = 10。特征加权网络的输入是一个1×266×8的高维特征矩阵,经过公式(3)与公式(4)计算即可得到一个经过自注意力机制加权之后的新特征矩阵A - score∈R10×8。
2.3 分类网络分类网络的主要作用是对特征加权网络输出的注意力特征矩阵进行分类。此网络首先将自注意力模块的输出特征矩阵A - score扁平化,获得一个长度为80的一维特征向量,并将其作为全连接层的输入,使用Softmax函数激活,分类层的输出为Y*,计算公式如下
| $ Y^*=\operatorname{Soft} \max (W \cdot \text { flatten }(A-\text { score })+b) $ | (5) |
式中,Y*即为预测标签,文中使用交叉熵损失函数衡量预测标签与真实标签之间的损失,优化器采用Adam函数。
3 实验及结果分析使用Python3.7进行开发,基于Keras构建上述干扰事件识别模型。下文介绍了模型的评价指标及对比实验模型,并对实验结果进行了分析。
3.1 评价指标基于深度学习技术识别一段给定的地磁场原始观测数据是否受到干扰事件影响,本质上属于二分类问题。为了评估模型的分类效果,使用准确率(accuracy)、精准率(precision)、召回率(recall)和F1 - Score分别进行评价。文中样本被划分为干扰样本和正常样本2种类型,对应的混淆矩阵见表 3所示,表中:TP(True Positive)为真正类,即样本本来为正常样本,预测结果也为正常样本,预测结果正确;FN(False Negative)为假反类,即样本本来为正常样本,但预测为干扰样本,预测结果错误;FP(False Positive)为假正类,即样本本来为干扰样本,但被预测为正常样本,预测结果错误;TN(True Negative)为真反类,即样本本来为干扰样本,预测结果也为干扰样本,预测结果正确。
| 表 3 混淆矩阵 Table 3 Confusion matrix |
准确率是指所有分类正确的样本占全部样本的比例,包含正常样本预测准确和干扰样本预测准确的情况,公式如下
| $ \text { accuracy }=\frac{\mathrm{TP}+\mathrm{TN}}{\mathrm{TP}+\mathrm{FP}+\mathrm{TN}+\mathrm{FN}} $ | (6) |
精确率是指在预测为正常样本中实际为正常(预测正确)数据个数的比例,公式如下
| $ \text { precision }=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}} $ | (7) |
召回率又称为查全率,即所有真实类别为正常样本的样本中,被预测为正常样本的样本比例,公式如下
| $ \text { recall }=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} $ | (8) |
在二分类实验中,每一类别均有其精准率和召回率。文中使用各个类别精准率和召回率的平均值作为模型最终的精准率和召回率。
F1 - Score是精准率和召回率的调和平均,兼顾了精准率和召回率,其定义公式如下
| $ \frac{1}{F_1-\text { Score }}=\frac{1}{2}\left(\frac{1}{\text { precision }}+\frac{1}{\text { recall }}\right) $ | (9) |
整理可得
| $ F_1-\text { Score }=\frac{2 \times \text { precision } \times \text { recall }}{\text { precision }+\text { recall }} $ | (10) |
只有精准率和召回率二者均为高值,其调和平均值才会是高值。若其中一项较低,调和平均则接近较低值。
3.2 对比实验模型地磁场观测数据是一种典型的时间序列数据,而深度学习则在时间序列数据分类、异常识别和预测等领域应用广泛,可见深度学习算法适用于地磁场干扰事件识别领域,只是至今鲜有研究人员开展此项研究。为了验证本研究模型实验结果的有效性,选择多层感知机(Multi Layer Perceptron,MLP)、全卷积网络(Fully Convolutional Neural Networks,FCN)和残差网络(Residual Network,ResNet)3种在时间序列数据应用广泛的深度网络模型开展对比研究。
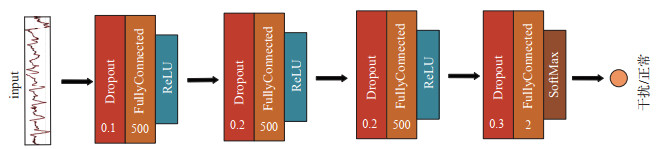
MLP是一种经典的、简单的前馈人工神经网络模型,相邻两层之间的神经元为全连接,其网络结构见图 5。除了输入层,该模型共包含4层,其中每一层都完全连接到其上一层的输出,最后一层是Softmax分类器,输出为正常样本或干扰样本的概率。中间3个隐层均由500个神经元组成,并选用ReLU作为激活函数。为了防止因模型的参数太多、训练样本少而导致模型出现过拟合的现象,除了Softamx层外,每层之后接一个Dropout操作,按照0.1、0.2、0.2和0.3的概率舍弃部分神经单元。
|
图 5 MLP网络模型 Fig.5 MLP network model |
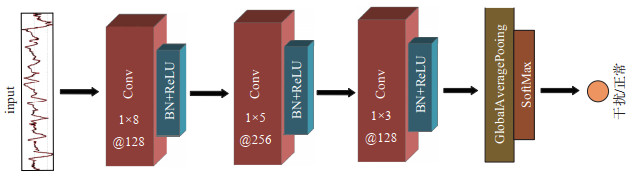
全卷积神经网络由Wang等(2022)首先提出,并将其用于单变量时间序列分类。FCN模型不包含任何本地池化层,用全局平均池层(Global Average Pooling,GAP)替代传统的全连接层(FC),减少了神经网络中参数的数量,网络结构见图 6。该网络由3个卷积模块组成,其中每个模块包含3个操作:卷积、批处理归一化(Batch Normalization,BN)和ReLU激活函数。第3卷积层的结果被送到全局平均池层,在整个时间维度上求平均值。最后,Softmax分类器输出正常样本和干扰样本的概率。所有卷积的滑动步幅均等于1,且两端用0填充。第1个卷积模块包含128个长度为1×8的卷积核,第2个卷积模块包含256个长度为1×5的卷积核,第3个卷积模块包含128个长度为1×3的卷积核。
|
图 6 FCN网络模型 Fig.6 FCN network model |
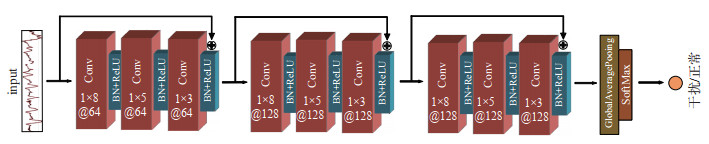
ResNet除了输入层,共有11层,其中前9层为卷积层,并被分为3个残差块,最后2层为全局平均池化层和Softmax层,网络结构见图 7。与常规卷积不同,ResNet通过快捷连接方式将残差块的输出链接至下一个残差块的输入,从而使梯度流直接通过这些连接流动。每个残差块由3个卷积层组成,卷积核大小分别设置为1×8、1×5和1×3。第1组残差模块中的卷积层过滤器数量固定为64个,第2组和第3组残差模块中的卷积层过滤器数量固定为128个。激活函数选择ReLU,引入BN层加快训练速度。
|
图 7 ResNet网络模型 Fig.7 ResNet network model |
在所有模型的实验中,最大迭代次数均设置为300次,并引入Early Stopping机制,防止模型因过度训练导致过拟合,以取得更好的泛化效果。本研究在模型训练过程中,通过监控模型在验证集上的准确率(val accuracy)来判断模型是否达到最优。如果模型在验证集上的损失在连续30次迭代(Epoch)后没有提升,则认为模型已达最优,结束训练。模型初始学习率设置为0.01。
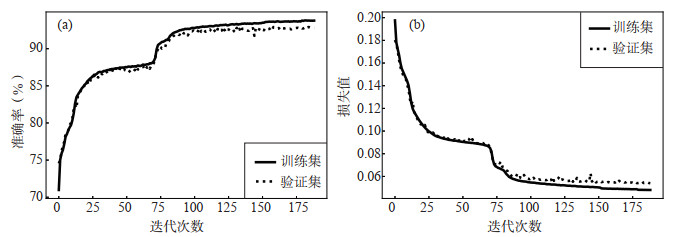
将样本训练集与验证集输入干扰事件识别模型进行训练。本研究模型训练过程中的模型准确率与损失变化见图 8,可见模型在迭代189次后停止训练,模型在训练集和验证集上的准确率分别为93.77%和92.93%,表明模型在训练集与验证集上的拟合情况较好,未发生明显的过拟合现象。
|
图 8 本研究模型训练过程中的准确率与损失变化曲线 (a) 准确率变化曲线;(b) 损失变化曲线 Fig.8 Thetrainingaccuracy and loss curve of the model this paper proposed |
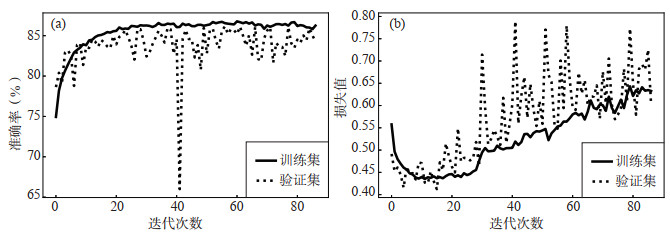
图 9、图 10和图 11分别显示了MLP、FCN和ResNet三个模型训练过程中准确率和损失的变化情况。由图 9可见,MLP在训练约20次时,训练集的准确率趋于平稳,损失曲线达最低点。随着迭代次数的增加,模型在训练集上的准确率基本处于稳定状态,但模型在验证集的准确率呈现大幅波动,无明显上升。此外,随着迭代次数的增加,MLP模型在训练集和验证集上的损失反而呈现逐渐上升趋势,且在验证集上的损失出现震荡,表明模型存在过拟合现象。最终,MLP在训练集和验证集上的准确率分别为86.88%、84.25%。
|
图 9 MLP训练过程中的准确率与损失变化曲线 (a) 准确率变化曲线;(b) 损失变化曲线 Fig.9 Thetrainingaccuracy and loss curve of MLP |
|
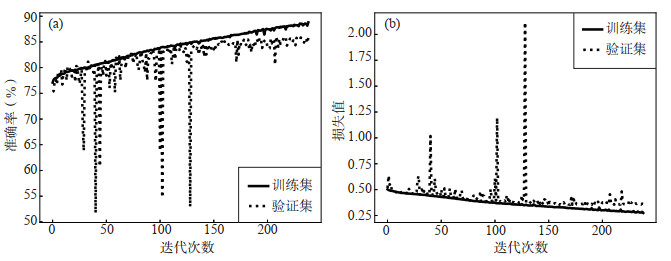
图 10 FCN训练过程中的准确率与损失变化曲线 (a) 准确率变化曲线;(b) 损失变化曲线 Fig.10 Thetrainingaccuracy and loss curve of FCN |
|
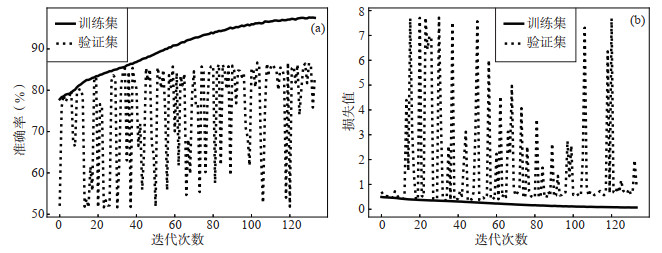
图 11 ResNet训练过程中的准确率与损失变化曲线 (a) 准确率变化曲线;(b) 损失变化曲线 Fig.11 Thetrainingaccuracy and loss curve of ResNet |
由图 10可知,随着迭代次数的增加,FCN在训练集上的准确率不断增加、损失逐步下降,但在验证集的准确率与损失先呈现震荡状态,在迭代150次之后,准确率增加缓慢,损失无明显下降,出现了较明显的过拟合现象。FCN在训练集和验证集上的准确率分别为85.87%和85.83%。
由图 11可知,随着迭代次数的增加,ResNet在训练集上的准确率呈上升趋势,损失呈下降趋势,但在验证集上的准确率与损失始终呈现震荡状态,存在较明显的过拟合现象。ResNet在训练集上的准确率为97.52%,为3种模型中的最高值,但在验证集上的准确率只有83.11%,为3种模型中的最低值,表明其泛化能力较差。
MLP、FCN、ResNet和本研究提出的干扰事件识别模型在训练集、验证集与测试集上的各评价指标得分统计结果见表 4。由表 4可知,在训练集上,ResNet模型的准确率得分最高,为97.52%,但该模型在验证集的准确率得分却最低,为83.11%,表明模型泛化能力较差。本研究所提出的干扰事件识别模型在验证集上的准确率最高,达92.93%,且仅比训练集上的准确率93.79%低0.86%,表明模型的泛化能力较强。在测试集上,本研究模型在准确率、召回率、精准率和F1 - Score四个指标中,均获得最高评分,分别为93.37%、93.40%、93.39%、0.933 9。按照F1 - Score指标统计,评分优劣次序为:本研究模型>FCN>MLP>ResNet,表明使用卷积操作的FCN网络效果整体上优于只使用全连接层的MLP网络。而网络层数最深的ResNet分类效果则表现最差,可能与时间序列内含特征较为简单有关。此外,本研究模型在测试集上的准确率、召回率、精确率均高于93.3%,并且与模型在训练集和验证集的结果类似,表明该模型比较稳定,泛化能力较好,具有一定的实用价值。
| 表 4 4种模型实验结果对比 Table 4 Comparison of experimental results of four models |
基于卷积神经网络和自注意力机制提出一种地磁场干扰事件识别深度网络模型。实验结果表明,本研究模型在测试集上的准确率达93.37%,召回率达93.40%,与MLP、FCN、ResNet三种模型相比,识别准确率和召回率更佳。该方法既避免了统计学方法严重依赖专家经验和自动化程度低的缺点,又避免了传统机器学习方法因手动特征提取不全面而导致识别精度不高和泛化能力不强的弱点,通过在大量样本数据中自动提取原始数据特征,实现快速、准确、自动地识别干扰事件。随着地磁干扰事件数量激增和地磁观测仪器大规模部署,本方法后期无需专家介入,可有效减少现有人工或半人工识别地磁场观测数据中干扰事件的工作量,是未来地磁场观测数据干扰事件识别技术研发的主要方向,并为识别其他地震前兆学科观测数据中的干扰事件提供了一种新思路。
为消除干扰事件对地磁场观测数据的影响,获取较高质量的地磁场数据,首先需要初步定位到干扰事件(干扰事件检测),然后准确识别该干扰事件(干扰事件识别),最后对受干扰影响的原始观测数据进行校正(数据预处理)。利用行业专家前期积累的干扰事件,检测和识别历史数据,开展基于深度学习技术的干扰事件识别技术研究,必须结合干扰事件检测和数据预处理技术,才能在实际应用中发挥其价值,而基于深度学习的干扰事件检测技术和数据预处理技术是正在研究的内容之一。此外,本研究将多种干扰事件归为一类,不同的干扰事件形态差异巨大,即使使用深度学习技术自动提取原始观测数据内含的数据特征也存在一定困难,导致模型训练后期在验证集上的准确率提升不甚明显。因此,针对不同类型的干扰事件开展多类别干扰事件识别是今后的研究内容。由于过长的时间序列数据会增加模型的训练成本,因此仅针对持续时间不超过2个小时的干扰事件开展研究,下一步将尝试采取数据压缩或降采样技术,处理更长持续时间的干扰事件识别技术研究,提高算法的实用性。
文中使用的地磁数据来自于中国地震局地球物理研究所国家地磁台网中心,在此表示感谢。
鲍海英, 蒋延林, 樊晓春, 等. 高压直流输电对地电场观测的影响探讨[J]. 中国地震, 2020, 36(3): 607-619. DOI:10.3969/j.issn.1001-4683.2020.03.022 |
程文凯, 杜劲松, 陈超, 等. 基于XGBoost机器学习的地磁日变重构方法研究[J]. 地震学报, 2021, 43(1): 100-112. |
樊俊屹, 刘高川, 王晓, 等. 地球物理台网观测环境干扰现状分析[J]. 地震地磁观测与研究, 2021, 42(3): 242-249. DOI:10.3969/j.issn.1003-3246.2021.03.030 |
韩明亮, 邹志辉, 马锐. 利用反射地震资料和多尺度训练集的深度学习速度建模[J]. 石油地球物理勘探, 2021, 56(5): 935-946. DOI:10.13810/j.cnki.issn.1000-7210.2021.05.001 |
李章, 李本有, 严吉, 等. 地磁数据缺失重构方法的研究[J]. 科技资讯, 2021, 19(17): 39-41. |
李正媛, 熊道慧, 刘高川, 等. 基于大数据挖掘的地震前兆台网观测数据跟踪分析[J]. 地震地磁观测与研究, 2016, 37(3): 1-6. |
廖绍欢, 李雪浩, 魏嘉曦. 成都地震基准台及其下属台站地磁干扰类型和数据预处理分析[J]. 四川地震, 2021(2): 36-41. |
刘军, 陈磊, 李文灿, 等. 基于混沌蚁群优化小波阈值法地磁信号噪声压制[J]. 科学技术与工程, 2020, 20(25): 10177-10181. DOI:10.3969/j.issn.1671-1815.2020.25.008 |
王静, 贺巍, 汪伟明. 基于离散Gabor变换的磁暴识别[J]. 地震地磁观测与研究, 2020, 41(4): 64-69. |
王军, 刘春国, 樊俊屹. 基于CNN的地震前兆台网观测数据异常图像识别方法[J]. 地震工程学报, 2021, 43(1): 28-32. |
王立辉, 刘庆雅, 许宁徽. 基于干扰检测和CEEMD的地磁信号降噪方法[J]. 中国惯性技术学报, 2020, 28(4): 474-479. |
杨晶, 丁仁伟, 林年添, 等. 基于深度学习的地震断层智能识别研究进展[J]. 地球物理学进展, 2022, 37(1): 298-311. |
杨学慧, 杨正纲, 姚休义, 等. 地磁观测数据中典型干扰识别与处理[J]. 高原地震, 2020, 32(3): 30-36. |
应允翔, 车濛琪, 刘红飞, 等. 安徽省地磁仪器观测质量分析[J]. 科技资讯, 2021, 19(22): 60-64. |
张帆, 杨晓忠, 吴立飞, 等. 基于短时傅里叶变换和卷积神经网络的地震事件分类[J]. 地震学报, 2021, 43(4): 463-473. |
周飞燕, 金林鹏, 董军. 卷积神经网络研究综述[J]. 计算机学报, 2017, 40(6): 1229-1251. |
Geng Y, Su L L, Jia Y H, et al. Seismic events prediction using deep temporal convolution networks[J]. Journal of Electrical and Computer Engineering, 2019, 2019: 7343784. |
Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Lake Tahoe, Nevada: Curran Associates Inc., 2012: 1 097-1 105.
|
Ku B, Kim G, Ahn JK, et al. Attention-based convolutional neural network for earthquake event classification[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 18(12): 2057-2061. |
Liu G C, Shan W F, Chen J, et al. Automatic classification and recognition of geomagnetic interference events based on machine learning[J]. Journal of Computational Methods in Sciences and Engineering, 2022, 22(4): 1157-1170. |
Perol T, Gharbi M, Denolle M. Convolutional neural network for earthquake detection and location[J]. Science Advances, 2018, 4(2): e1700578. |
Purwins H, Li B, Virtanen T, et al. Deep learning for audio signal processing[J]. IEEE Journal of Selected Topics in Signal Processing, 2019, 13(2): 206-219. |
Qian B, Xiao Y, Zheng Z J, et al. Dynamic multi-scale convolutional neural network for time series classification[J]. IEEE Access, 2020, 8: 109732-109746. |
Ramachandran P, Parmar N, Vaswani A, et al. Stand-alone self-attention in vision models[C]//Proceedings of the 33rd International Conference on neural Information Processing Systems. Vancouver, Canada: Curran Associates, Inc., 2019: 68-80.
|
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]//Proceedings of the 31st International Conference on neural Information Processing Systems. Long Beach, California, USA: Curran Associates Inc., 2017: 6 000-6 010.
|
Wang W H, Xie E Z, Li X, et al. PVT v2: Improved baselines with Pyramid Vision Transformer[J]. Computational Visual Media, 2022, 8(3): 415-424. |
Xu X, Huang L, Liu X J, et al. Deepmad: Deep learning for magnetic anomaly detection and denoising[J]. IEEE Access, 2020, 8: 121257-121266. |
Yin C Y, Zhang S, Wang J, et al. Anomaly detection based on convolutional recurrent autoencoder for IoT time series[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(1): 112-122. |
 2022, Vol. 43
2022, Vol. 43

