2) 中国南京 210014 江苏省地震局
2) Jiangsu Earthquake Agency, Nanjing 210014, China
通常,随着地震台站的增多和测震台网的升级改造,最小完整性震级会减小,区域测震台网监测能力的及时动态评估,是进行余震序列类型研究、地震预报b值估计、地壳速度结构区域探查、地震地质等科学研究的重要基础(Stein,1999;Knopoff,2000;Main,2000;Wiemer and Wyss, 2000;Gomberg et al,2001;Enescu and Ito, 2002;Woessner et al,2004;冯建刚等,2012)。测震台网的观测资料是开展地震监测预报业务的重要基础支撑,台网的地震监测能力在一定程度上影响了测震台网地震观测资料的质量优劣,因此对测震台网的地震监测进行科学的、准确合理的评估,对于地球科学的基础研究具有重要作用。
目前,区域测震台网监控能力评估多基于统计地震学方法,主要有2种方法:①假定震级—频度满足G-R关系,例如完整性震级范围(简称EMR)方法(Ogata et al,1993)、最大曲率(英文简称MAXC)方法以及拟合度监测(简称GFT)方法(Wiemer et al,2000)等;②基于理论评估不假定G-R关系的方法,例如基于概率的完整性震级(英文简称PMC)方法(Schorlemmer et al,2008)、贝叶斯完整性震级(简称BMC)方法(Mignan et al,2011,2013)等。目前,常规评估方法有PMC方法、EMR方法和震级—最大距离方法(中国地震局监测预报司,2003),获得的最小完整性震级分别表示为MP、Mc及Mr,其中PMC方法因其评估误差低、精度高而受到广泛关注。如:王亚文等(2017)研究表明,在南北地震带的个别地区,不同方法在地震监测能力评估中,实践应用效果差异显著,最小完整性震级差值可达ML 2.0,在统计均值上具有Mc<MP<Mr的关系,考虑到实际地震台网的空间布局,仍推荐使用PMC方法进行地震监测能力评估;Schorlemmer和Woessner(2008)将PMC技术和EMR方法用于南加州地区地震监测能力评估,发现在大部分点位上MP<Mc,表明PMC技术的应用效果更佳;Nanjo等(2010)基于PMC方法得到瑞士地震监测能力评估结果,尝试优化瑞士地震台网布局;李智超等(2014)采用PMC方法评估首都圈地区地震台网检测能力,发现基于测震台网和单台的最小完整性震级均呈现逐步降低趋势,通过增加虚拟台站进行模拟计算,证实其在测震台网检测能力的有效性,有利于首都圈台网今后建设。此外,刘芳等(2014)、蒋长胜等(2015)、王鹏等(2016, 2020)、安祥宇等(2019)、司政亚等(2021)采用PMC方法,分别得到内蒙古、首都圈、山东、辽宁、上海测震台网的地震监测能力。
青海省地处构造运动强烈、断裂带发育的青藏高原北部,是我国大陆地区强震多发省份之一。其地震监测系统工作最早可追溯至1953年,1972—1980年是系统奠定基础的主要时期,后经“九五”“十五”“十一五”规划发展,台网数字化改造完成,地震监控能力得到显著提升。受地域条件和外部环境限制,青海省地震台网建设存在明显的区域不平衡现象。此外,台站优化改造及设备的更新换代、台站搬迁及人类活动等均对地震监测能力造成了一定影响,其结果直接影响到相关研究的可信度,及时对台站仪器监测能力进行评估是优化台网建设的重要任务之一。因此,将基于概率的完整性震级(PMC)方法引入青海区域,计算单台检测概率PD、测震台网合成检测概率PE以及基于概率的最小完整性震级MP,通过考察MP对地震事件监控能力的真实反映,分析测震台网记录地震的完整程度,为优化台网布局奠定基础。
1 PMC方法的计算原理PMC方法的资料选取基于地震编目系统产出的正式观测报告(包括台站代码、震中经纬度、发震时刻、震级、震中距等参数)。采用PMC算法计算每个台站对周围所发生地震的时空监测能力(Schorlemmer et al,2008),所得结果与台站分布、台基噪声、台站密度密切相关。具体计算步骤如下:
(1)计算单台检测概率PD。据刘芳等(2014)的研究,单台检测概率的可靠性需符合以下条件:①规定台网对地震的触发条件不变,采用全国各区域相同的地方震震级的测定定义;②将每个地震参数标注在震级—震中距的二维空间中,作为原始数据;③根据地方震震级的测量定义,得到震级与震中距之间的关系。计算原理如下:
震级随距离的衰减关系为
| $ M=c_1 \lg A-c_2 \lg L^*+c_2 $ | (1) |
式中,L*为震中距,对于某一台站,假设记录的2个事件震中距离为L1、L2,振幅均为A,则对应震级为
| $ M_1=c_1 \lg A-c_2 \lg L_1+c_3 $ | (2) |
| $ M_2=c_1 \lg A-c_2 \lg L_2+c_3 $ | (3) |
将式(2)减式(3)可构建M与L的经验转换关系
| $ \Delta M^*=c_2 \lg L_1-c_2 \lg L_2 $ | (4) |
式中,ΔM*为震级差。青海省测震台网采用全国统一的MSDP软件,即在仿真短周期位移记录(伍德—安德森)上量取S波或Lg波最大振幅进行震级测定(中国地震局监测预报司,2003),公式如下
| $ M_{\mathrm{L}}=\lg A+R(L) $ | (5) |
式中:R(L)为量规函数。由此,式(4)中ΔM*仅与量规函数R(L)有关。据Schorlemmer和Woessner(2008)的定义,假设台站记录到周边某次地震(M′,L′),与位置(M,L)的地震对应的震级差为ΔM = (M′- M),加入震中距,代入式(4)可得ΔM* = R(L′) - R(L)。阈值选取满足(Schorlemmer et al,2008;Gentili et al,2011)
| $ L_M=\sqrt{\Delta M_2+\Delta M^{* 2}} \leqslant 0.1 $ | (6) |
假设地震数目Nt≥10,台站检测到的地震数记为N+,未被检测到的地震数记为N-,则单台检测概率PD(M, L)为
| $ P_{\mathrm{D}}(M, L)=\frac{N_{+}}{N_{+}+N_{-}} $ | (7) |
(2)计算合成检测概率PE。据Schorlemmer等(2008)所述,PE(M, x, t)为在空间x位置t时刻的某一地震至少被4个台站记录的联合概率,由1 - PEi得到,公式如下
| $ {P_{\rm{E}}}(M, x, t) = 1 - \sum\nolimits_{i = 0}^3 {P_{\rm{E}}^i} $ | (8) |
其中:PE0、PE3分别表示由0个、3个台站记录所得概率。
对于所有震级档,得到最小完整性震级MP(x, t),公式如下
| $ {M_{\rm{P}}}(x, t) = \mathop {\min }\limits_{M \in {M_0}} M\mid \left({{P_{\rm{E}}}(M, x, t)} \right) = 1 - Q $ | (9) |
其中:取Q = 0.000 1(误差标准),M0为可能的地震区间(刘芳等,2014)。
2 台网建设及资料选取1953年,中国科学院地质与地球物理研究所在青海省首次布设测震台站,拉开了青海地震监测工作的序幕;1972—1980年,先后建设9个专业地震台,即门源、西宁、乌兰、香日德、玛多、格尔木、大武、德令哈、湟源,承担青海省地震监测工作;1981—1994年,地震检测进入模拟记录时期;1995—2005年,分为2个时期:“九五”(1996—2000年)期间,地震监测技术从模拟向数字技术跨越,“十五”(2001—2005年)期间,全省地震台网进入数字化规划建设;截至2005年,青海省地震监测台网由20余个地震台组成(青海省地方志编纂委员会,2018);截至2021年,青海省测震台网已发展到69个数字测震台站,包括“‘十五’项目台站”“背景场项目台站”“青藏高原监测能力提升项目2019年新建台站”“青藏高原监测能力提升项目2020年新建台站”“青藏高原监测能力提升项目2021年新建台站”,同时引入甘肃、新疆、四川、西藏等邻省地区26个台站组成地震监测网络,青海地区地震监测能力明显提升。截至2021年,青海及邻区测震台站分布见图 1,可见研究区台站分布不均匀,其东部和东南部地区台站密度较大,中部、北部、西部、南部地区站点分布较为稀疏。
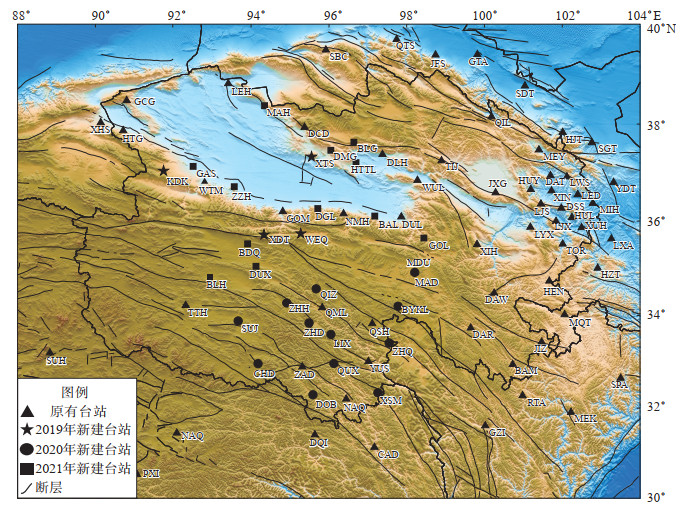
|
图 1 青海及邻区测震观测台站 Fig.1 Distribution of seismic observation stations in Qinghai Province and its adjacent area |
以青海地区(31°—40°N,88°—104°E)为研究区域,以青海测震台网稳定运行时段2014—2021年的地震观测报告数据为研究对象,共得到ML≥0.0地震24 964次,采用PMC方法对研究区地震监控能力进行评析。PMC方法是以概率为基础的统计学方法,地震数充足,才能充分反映地震台网的实际监测能力,计算结果才会更加稳定。青海及邻区位于地震活动频繁、现今构造活动强烈的青藏高原东北缘,其特殊性,为PMC方法的计算结果稳定性提供了有利保障。
3 单台检测概率计算和分析单台检测概率PD是PMC方法的基础内容,可以作为评估地震台网监测能力的定量指标之一。选取被≥4个台站记录的地震事件,通过计算获得69个台站的单台检测概率PD。为了能直观反映青海及邻区测震台网对地震事件检测能力的差异,使用以下条件评估(刘芳等,2014):①单台记录ML 1.0地震的最大震中距;②单台记录ML 3.0地震的最大震中距;③单台记录震中距L = 100 km地震的最小震级;④单台记录震中距L = 300 km地震的最小震级。按以上设定,统计得到青海测震台网69个台站的单台监测能力,结果见表 1。满足上述评估条件越多的台站,表明其单台地震监测能力越好,据此可知,研究区37个台站地震监测能力较好,32个台站(含29个2019年以来新架设台站)监测能力较差。新建台站监测能力差主要是因为,台站尚未验收,运行时间短,小震资料在定位过程中使用率低,且在编目过程中,为确保震相位置精准并保证地震编目质量,会人为剔除初至震相不清晰、台站空隙角过大的台站数据,直接影响了其单台检测能力。
| 表 1 青海测震台网单台检测概率统计 Table 1 Statistics of single station detection probabilities of the Qinghai Seismic Network |
由表 1可知,青海区域地震台网台站监测能力具有以下区域特征:①青海东部地区(32°—38°N,99°—104°E):24个台站中有23个台小震监测能力较高,仅西宁台监测能力较差,建议维护;②中北部地区(36°—40°N,88°—99°E):21个台站中有8个台,即都兰、诺木洪、格尔木、乌图美仁、花土沟、干柴沟、冷湖、德令哈台小震监测能力较高,小黑山、大柴旦台监测能力稍低,11个新建台站监测能力较差;③中南部地区(32°—36°N,88°—99°E):24个台站中有6个台,即沱沱河、杂多、囊谦、玉树、清水河、曲麻莱台小震监测能力较高,18个新建台站监测能力较差。经验证,单台检测概率统计结果与实际地震监测能力相符,说明上述评估条件设定在青海地区是可行的。以门源、兴海、花土沟台记录为例,验证单台检测概率评估条件的可行性,结果见图 2。
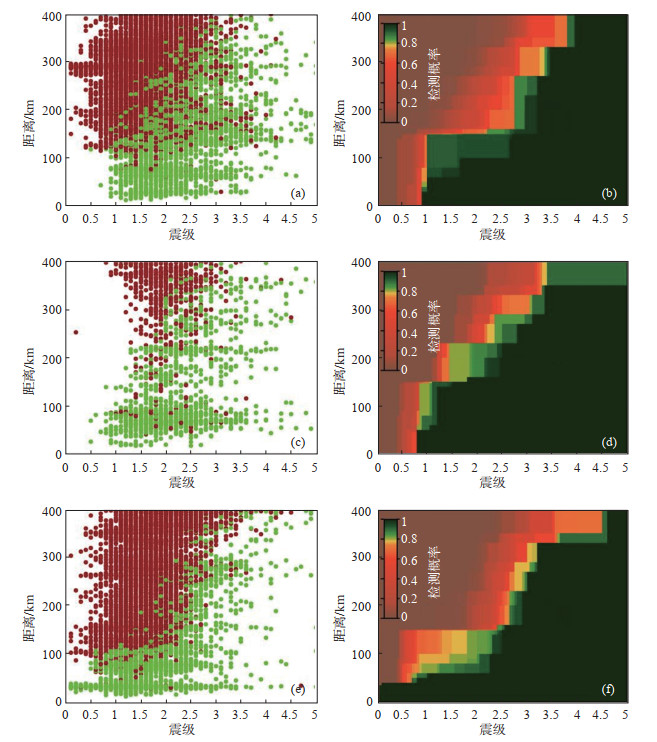
|
图 2 青海测震台网个别台站检测概率 (a)、(c)、(e)为兴海台、花土沟台、门源台震级—距离原始点阵图(红点为在台站附近发生但未被台站记录地震,绿点为台站实际记录地震);(b)、(d)、(f)为兴海台、花土沟台、门源台基于PMC监测方法的单台检测概率(色标表示对应震级—震中距检测能力概率) Fig.2 Detection probabilities of the individual stations of the Qinghai Seismic Network |
门源台位于祁连山地震带中东段冷龙岭北侧断裂附近,青藏高原隆起区东北缘,周围地震活动较强,历史上强震多发,2022年1月8日青海门源MS 6.9地震和2016年1月21日门源MS 6.4地震即发生在此处;兴海台位于共和同德盆地西侧,附近构造活动特征明显,褶皱和断裂发育;花土沟台地处茫崖凹陷带附近,茫崖地区褶皱和断裂发育,是中强地震多发地带。3个台站台基水平较高,系统运行质量较好,记录地震在点位及编目工作上使用率较高,地震监测能力较好。由图 2可见:震中距L越大,记录的地震震级也越大(图中绿色圆点所示)。其中,门源台在ML 1.0时PD达100%,检测震级下限甚至可达ML 0.1,在震中距60 km范围内,该台对ML 0.1—2.3地震的检测能力达100%,表明该台具有较高的检测能力。同时,通过查看门源台、兴海台、花土沟台震级—距离原始点阵图,发现3个台站参与了大量地震事件的定位,震中距密集分布在100 km范围内。
4 PE、MP空间分布特征利用合成检测概率PE,计算基于概率的完整性震级MP,二者具有基本一致性,可用来评价测震台网监测能力。基于69个台站的单台检测概率,获得ML 1.0—5.0各震级档的合成检测概率,其中ML 1.5、ML 2.0、ML 2.5地震的合成检测概率PE空间分布见图 3中(a)、(b)、(c)图,完整性震级MP空间分布见图 3(d)。
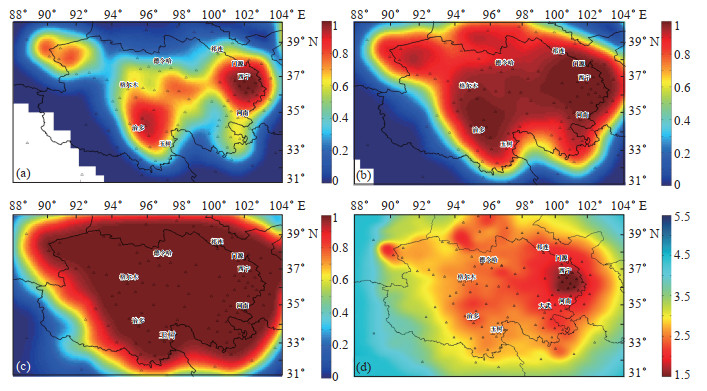
|
图 3 合成检测概率分布及MP空间分布特征 (a)ML 1.5地震检测概率的空间分布;(b)ML 2.0地震检测概率的空间分布;(c)ML 2.5地震检测概率的空间分布;(d)MP空间分布 Fig.3 Synthetic detection probability distribution and MP spatial distribution characteristics |
由图 3(a)可见,青海东部地区,即门源—西宁—海东—海南—黄南一带对ML 1.5地震的检测概率较强,PE可达100%左右;在治多一带,对ML 1.5地震的合成检测概率PE可达90%左右。由图 3(b)可见,对于ML 2.0地震,青海地区约85%的区域合成检测概率PE达100%,仅在青藏交界中西部地区合成检测概率较低,约10%。由图 3(c)可见,对于ML 2.5地震,青海地区90%的区域合成检测概率可达100%,但在青藏交界西部地区,PE较低,约20%。由图 3(d)可见,受台站布局和密度的影响,研究区MP空间分布不均,表明青海测震台网监测能力分布并不均衡,其中:台站较为密集的东部地区监测能力较好,MP为ML 1.5—2.0;中部次之,MP为ML 1.8—2.5;在台站较为稀疏的青海西部和南部地区,监测能力相对较差,西部地区MP为ML 2.5—3.5,南部地区MP为ML 2.2—2.7;青藏交界中西部监测能力最差,MP约为ML 2.5—3.5。通过对比MP与某一震级档PE的空间分布,发现二者对青海测震台网监测能力的指示作用基本一致,其中PE对某一震级档地震的检测更加精细,而最小完整性震级MP的空间分布则可更直观地反映青海测震台网地震监测能力。随着29个新建台站积累的地震资料越多,青海地区地震监测能力的提升空间将会更大。
5 结论和讨论 5.1 结论通过PMC方法求取青海测震台网69个台站的单台检测概率PD和ML 1.0—5.0各震级档的合成检测概率PE,对青海区域最小完整性震级MP的计算结果进行评估分析,结果表明:
(1)青海测震台网单台检测概率可以直观反映各台站对不同震级、不同震中距地震的检测能力,有利于台网布局优化及台站整改维护,加深对测震台网布局的了解,提高台站运维水平。
(2)合成检测概率PE可较为客观地反映台站对地震事件的实际检测情况,对某一震级档的地震检测能力更为精细,对于ML 1.5地震,在青海东部地区和治多一带检测能力较强;对于ML 2.0地震,青海地区约85%的区域检测能力可达100%;对于ML 2.5地震,青海地区约90%的区域检测能力可达100%,仅青海与西藏交界地区检测能力较差,PE约10%。
(3)由青海地区最小完整性震级MP分布结果可知,青海测震台网地震监测能力并不均衡,东部强,中部次之,西部和南部地区相对较差,青藏交界区域最差。这种不平衡性主要受台站密度、共享台站位置及数量的影响,其中:东部地区台站分布密集,检测概率显著高于其他地区;青海东部地区共享接入甘肃省地震局和四川省地震局的18个台站数据,使得检测能力明显提升,而青海西部和南部地区仅接入新疆和西藏的6个台站数据。此外,由于地震编目工作精度的要求,将剔除震中距过远、震相不清晰、空隙角过大的台站数据,导致新建台站检测概率降低,进而造成局部区域合成检测概率PE偏低。
5.2 讨论使用PMC方法评估测震台站监测能力,要求台站附近地区地震活动具有均匀性,而实际上,断层发育所致地震活动的丛集性,使得地震分布不均匀,尽管计算时已经删除多数丛集地震,但仍会对结果产生一定影响。同时,PMC方法对不同方位的地震分布具有各向同向性(刘芳等,2014),与实际情况会有差异。但是,PMC方法有其独特优点,在空间上“无缝”衔接,不会因地震覆盖过少而出现地震空区,评估MP震级不需要假定震级分布关系,使对估计区域地震台网整体空间分布的完整性成为可能,且评估震级误差低于0.1。此外,利用不同地震监测能力评估方法所得结果可能有所不同,其差异性备受关注。本研究所得地震监测能力评估结果与其他方法在青海地区地震监测中的应用存在一定差异,例如:在同一区域,与韩立波等(2012)利用EMR方法得到的Mc结果相当,但与2016年“震级—序号”法所得Mc约存在0.5的偏差;在同时段、同区域,与余娜等(2020)用多参数方法计算的Mc值,除青藏交界地区差别较大外,其他地区估算结果大体一致。分析认为,利用“震级—序号”法所得Mc值在ML 1.0以下,是因为受到2016年1月门源MS 6.4地震较多小余震的影响;利用多参数方法所得青藏交界地区Mc值偏高,由该区域台站较少、记录地震数过少所致。
内蒙古自治区地震局刘芳提供了基于PMC方法的计算程序,江苏省地震局顾勤平在本文撰写过程中给予指导,审稿专家亦对本文的完善提出了诸多宝贵意见,在此一并表示感谢。
安祥宇, 赵倩, 王晓睿, 等. 基于PMC方法的辽宁测震台网监测能力评估[J]. 地震工程学报, 2019, 41(6): 1545-1552. DOI:10.3969/j.issn.1000-0844.2019.06.1545 |
冯建刚, 蒋长胜, 韩立波, 等. 甘肃测震台网监测能力及地震目录完整性分析[J]. 地震学报, 2012, 34(5): 646-658. DOI:10.3969/j.issn.0253-3782.2012.05.006 |
韩立波, 蒋长胜, 李艳娥, 等. 用于地震可预测性CSEP计划的南北地震带地区地震最小完整性震级Mc研究[J]. 地震, 2012, 32(1): 17-27. |
蒋长胜, 房立华, 韩立波, 等. 利用PMC方法评估地震台阵的地震检测能力——以西昌流动地震台阵为例[J]. 地球物理学报, 2015, 58(3): 832-843. |
刘芳, 蒋长胜, 张帆, 等. 内蒙古区域地震台网监测能力研究[J]. 地震学报, 2014, 36(5): 919-929. |
李智超, 黄清华. 基于概率完备震级评估首都圈地震台网检测能力[J]. 地球物理学报, 2014, 57(8): 2584-2593. |
青海省地方史志编纂委员会. 青海省志-地震志[M]. 西宁: 青海人民出版社, 2018: 100-146.
|
司政亚, 钟世军, 林向东, 等. 基于PMC方法分析北京及邻区地震监测能力[J]. 地震地磁观测与研究, 2021, 42(Z1): 70-72. DOI:10.3969/j.issn.1003-3246.2021.S1.023 |
王鹏, 郑建常, 李铂. 基于PMC方法的山东省测震台网监测能力评估[J]. 地球物理学进展, 2016, 31(6): 2408-2414. |
王鹏, 毕波, 林航毅, 等. 基于PMC方法的上海测震台网地震监测能力评估[J]. 地震地磁观测与研究, 2020, 41(5): 18-24. |
王亚文, 蒋长胜, 刘芳, 等. 中国地震台网监测能力评估和台站检测能力评分(2008-2015年)[J]. 地球物理学报, 2017, 60(7): 2767-2778. |
余娜, 张晓清, 杨晓霞. 青海及邻区地震目录最小完整性震级分析[J]. 地震, 2020, 40(4): 23-32. |
中国地震局监测预报司. 数字地震观测技术[M]. 北京: 地震出版社, 2003: 521-522.
|
Enescu B, Ito K. Spatial analysis of the frequency-magnitude distribution and decay rate of aftershock activity of the 2000 Western Tottori earthquake[J]. Earth, Planets and Space, 2002, 54(8): 847-859. |
Gentili S, Sugan M, Peruzza L, et al. Probabilistic completeness assessment of the past 30 years of seismic monitoring in northeasternItaly[J]. Phys Earth Plane Inter, 2011, 186(1/2): 81-96. |
Gomberg J, Reasenberg P A, Bodin P, et al. Earthquake triggering by seismic waves following the Landers and Hector Mine Earthquakes[J]. Nature, 2001, 411(6 836): 462-466. |
Knopoff L. The magnitude distribution of declustered earthquakes in Southern California[J]. Proc Nat Acad Sci USA, 2000, 97(22): 11880-11884. |
Main I. Apparent Breaks in Scaling in the Earthquake Cumulative Frequency-Magnitude Distribution: Fact or Artifact[J]. Bull Seismol Soc Am, 2000, 90(1): 86-97. |
Mignan A, Werner M J, Wiemer S, et al. Bayesian estimation of the spatially varying completeness magnitude of earthquake catalogs[J]. Bull Seismol Soc Am, 2011, 101(3): 1371-1385. |
Mignan A, Jiang C, Zechar J D, et al. Completeness of the Mainland China earthquake catalog and implications for the setup of the China earthquake forecast testing center[J]. Bull Seismol Soc Am, 2013, 103(2A): 845-859. |
Nanjo K Z, Schorlemmer D, Woessner J, et al. Earthquake detection capability of the Swiss Seismic Network[J]. Geophysical Journal International, 2010, 181(3): 1713-1724. |
Ogata Y, Katsura K. Analysis of temporal and spatial heterogeneity of magnitude frequency distribution inferred from earthquake catalogues[J]. Geophysical Journal International, 1993, 113(3): 727-738. |
Stein R S. The role of stress transfer in earthquake occurrence[J]. Nature, 1999, 402(6762): 605-609. |
Schorlemmer D, Woessner J. Probability of Detecting an Earthquake[J]. Bull Seismol Soc Am, 2008, 98(5): 2103-2117. |
Wiemer S, Wyss M. Minimum Magnitude of Completeness in Earthquake Catalogs: Examples from Alaska, the Western United States, and Japan[J]. Bull Seismol Soc Am, 2000, 90(4): 859-869. |
Woessner J, Hauksson E, Wiemer S, et al. The 1997 Kagoshima (Japan) earthquake doublet: A quantitative analysis of aftershock rate changes[J]. Geophysical Research Letters, 2004, 31(3): L03605. |
 2022, Vol. 43
2022, Vol. 43


