0 引言

在地震台站的日常观测中，因地震计内部构造精密，故实际观测性能会受到外界环境的影响。地震计记录到的波形包括天然地震、人工爆破、地脉动波形、环境噪声（气流、海浪、人文、气压、温度等噪声）等，其中不是由天然地震产生的波形称之为背景噪声。地震台站的背景噪声水平直接决定了台站的地震记录能力，因此对背景噪声进行量化分析是研究台站噪声水平的首要步骤。Peterson（1993）通过研究全球范围的75个固定地震台站，给出地球正常噪声新模型来衡量地震台站的噪声水平。由此研究得出的地球高噪声模型（new high noise model，简写为NLNM）和地球低噪声模型（new low noise model，简写为NLNM），适用于全球所有地震台站。在Peterson（1993）的基础上McNamara等（2004）首次提出基于传统的噪声功率谱密度（power spectral density，简写为PSD）的分析方法，并分析了美国大陆的背景噪声水平，提出了用概率密度函数（probability density functions，简写为PDF）统计分析地震观测台站噪声水平的方法。该方法区别于传统的PSD方法，在计算中不需要排除地震在内的突发事件，这样就方便了选取连续性的波形数据，因此可以得到更准确的地震计噪声特性。此后，刘旭宙等（2018）研究认为，PDF方法可以有效判断不同观测仪器在相同观测环境下的细微差别，对不同仪器观测性能的差别给出量化、直观的结果。谢江涛等（2018）研究发现，地震台站连续观测波形的功率谱密度概率分布，对人为的活动、车辆等高频干扰以及地震事件反应较好，可以较好反应出地震监测台站的数据记录质量。在使用地震计之初，台站观测就一直存在环境干扰带来的监测能力不足的困扰，李雷等（2017）通过对比昆明地震台地面、井下宽频带地震计背景噪声，发现基岩地区井下观测可有效减少高频噪声干扰，高频噪声干扰即人为活动造成的噪声干扰。葛洪魁等（2013）研究认为，地震观测中的噪声主要包括人为噪声、微震噪声和风、大气压、温度等因素引起的自然噪声。人为噪声集中在短周期频段和高频频段，自然噪声集中在长周期频段。此外，通过研究噪声功率谱密度还可以为改进地震计的综合性能提供有力依据，安全等（2019）通过计算噪声功率谱密度的方法研究了地震计保温效能；此后，安全等（2021）用相同的方法评估了内蒙古区域测震台站背景噪声水平，也得到了较好结果。

本文拟通过对比乌加河地震台与乌力吉地震台不同观测环境所记录数据的PDF，定量观察2个台站台基背景噪声之间的差异，深入理解背景噪声对观测性能的影响，旨在为探究降低背景噪声方法提供参考。

1 乌加河地震台、乌力吉地震台简介

乌加河地震台位于内蒙古自治区巴彦淖尔市境内的阴山山脉南麓，观测洞体深约130 m，基岩为古生代闪长岩，观测室温度日变化不超过0.02 ℃，年变化不超过0.50 ℃。该台的台基条件较好，在“十五”数字地震观测网络项目中装配了JCZ-1型超宽（360—50 Hz）带地震计、BBAS-2型加速度计、EDAS-24GN6型数据采集器，提高了地震监测动态范围和频带宽度。数据采集器采样率为100 sps，动态范围大于140 dB；BBAS-2型加速度计的频带范围为DC—80 Hz，采样率为200 sps，动态范围大于130 dB。从2001年运行以来，该地震台一直为内蒙古测震台网乃至全国测震台网中记录能力较好的台站。近年来，随着台站周边交通状况的不断改善，特别是国道335的修建，乌加河地震台的记录能力逐渐减弱。本文即在此背景下拟量化分析乌加河地震台观测性能受干扰的程度。

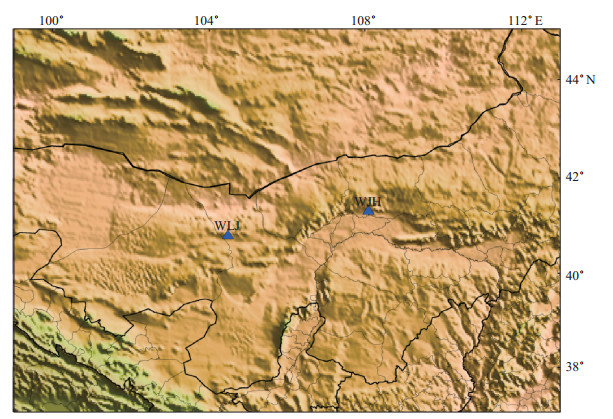
乌力吉地震台位于阿左旗北部，东与敖伦布拉格镇、巴盟乌拉特后旗接壤，南与吉兰泰镇、巴彦诺尔公苏木毗邻，西与阿右旗阿拉腾敖包镇相连，北与蒙古国交界。自然地形为南高北低，地貌以戈壁、荒漠、丘陵为主，区域气候受到海拔高度和沙漠的影响，干旱少雨，光、风资源较丰富，而水资源奇缺。干旱少雨的沙漠地形导致乌力吉日温差可达20 ℃，年温差可达60 ℃。台站基岩为花岗岩，台站配备了BBVS-120型甚宽频（120—50 Hz）带地震计和24位数据采集器。该台的观测方式为地面观测，较大的温差会对地震计所记录到的波形产生一定影响。本文拟定量研究乌力吉地震台观测数据受温度等的影响程度，以期为今后在沙漠中新建地震台提供一定的理论依据。台站信息及台站地理位置见表 1、图 1。

2 数据处理方法 2.1 数据预处理

使用乌加河地震台、乌力吉地震台原始波形，并进行预处理。由于采用PDF方法，该方法在计算中不需要排除地震在内的突发事件及观测系统的瞬态变化、仪器毛刺（如数据记录阶跃、限幅、尖峰、标定）等信号，因此，拾取的波形数据中没有去除上述信号，利用此方法可以得到更精确的地震台站台基噪声特性图。

2.2 计算功率谱密度

通过对随机稳态的离态波形数据进行傅里叶变换，可估算出噪声功率谱密度。

对周期时间序列y(t)的有限范围，傅里叶变换可表示为

$ Y\left({f, {T_r}} \right) = \int_0^{{T_r}} {\rm{y}} (t) \cdot {{\rm{e}}^{ - i2{\rm{ \mathsf{ π} }}ft}}{\rm{d}}t $

(1)

式中，T_r为时间序列长度；f为频率。对离散频率值f_k，傅里叶变换定义为

$ Y_k=\frac{Y\left(f_k, T_r\right)}{\Delta t} $

(2)

式中，f_k = k/(NΔt)，其中，k=1，2，3，…，N-1；Δt为采样间隔（0.01 s）；N=T_r /Δt为截取时间段的采样点数。

根据维纳—辛钦定理，PSD定义为

$ P_k(f)=\frac{2 \Delta t}{N}\left|Y_k\right|^2 $

(3)

对波形数据进行去均值、去长周期成分，将每小时波形分为13段，设采样率为100 Hz，则1 h的功率谱密度值由13段功率谱密度值进行平均得到。

地震计记录的连续波形数据为地脉动速度量，采用下式将速度PSD值转换为加速度PSD值

$ P_{\mathrm{a} k}(f)=(2 {\rm{ \mathsf{ π} }} f)^2 P_k(f) $

(4)

式中，P_k为速度功率谱密度；P_ak为加速度功率谱密度。

在仪器频带范围内计算噪声功率谱时，仪器传递函数对结果的影响不大。但如果超出频带范围，超出的频带范围越远，仪器自噪声等因素的影响越大。在超出频带范围的计算中若没有扣除仪器传递函数，PSD曲线将明显失真，所以需要扣除仪器传递函数的影响，以真实反映地噪声物理量值

$ {\rm{PS}}{{\rm{D}}_{\rm{a}}} = \frac{{{P_{{\rm{a}}k}}}}{{{{\left. {|H(s){|^2}} \right|}_{s = i \cdot 2{\rm{ \mathsf{ π} }}f}}}} $

(5)

式中，PSD_a为真实地面运动加速度功率谱；H(s)为系统传递函数。

2.3 平滑处理

为了得到PSD在频域对数坐标中呈等间隔均匀分布，采用1/3倍频积分作平滑处理

$ \operatorname{PSD}_{\mathrm{a}}\left(f_{\mathrm{c}}\right)=\frac{1}{n} \sum _{f_1}^{f_{\mathrm{h}}} \operatorname{PSD}_{\mathrm{a}}(f) $

(6)

其中，f₁ = 2^-1/6f_c为频带下限频率；f_h = 2^1/6f_c为频带上限频率；n为介于二者之间频率f的个数。由式（6）得到中心频率f_c的PSD_a（f_c）平均值PSD_a（f_c），将其作为f_c加速度的PSD值，中心频率f_c以1/9倍频程为增加步长，即下一个中心频率f_c^k+1与当前中心频率f_c^k的关系为f_c^k+1 = f_c^k2^1/9，按照新的中心频率重新计算相应的f₁和f_h，然后将新的f₁和f_h之间的PSD值平均值作为下一个中心频率f_c的PSD取值。如此，在f_c的取值范围0.02—40.00 Hz内，每个记录段的PSD平均值赋予中心频率依次在对数坐标系呈等间隔随频率变分布。

2.4 计算概率密度函数

每个中心频率f_c的PSD概率密度函数为

$ P_{\mathrm{PSD}}\left(f_{\mathrm{c}}\right)=N_{\mathrm{p} f_{\mathrm{c}}} / N_{f_{\mathrm{c}}} $

(7)

其中，N_fc为f_c频点的记录段总数；N_Pfc为f_c频点的PSD值落在某PSD取值范围内的记录段个数，在本研究中PSD窗长与步长都取1 dB，变化范围为-200— -50 dB。然后，以f为横坐标，以PSD为纵坐标，以P_PSD(f_c)为色块绘制三维平面图，得到PDF分布图，不同色块代表某频点在一定PSD窗内功率谱概率数。

台站环境背景噪声水平的速度均方根值（RMS）计算公式为

$ \mathrm{RMS}=\left[P_k(f) *\left(f_{\mathrm{h}}-f_1\right)\right]^{1 / 2}=\left[P_k(f) * f_{\mathrm{c}} * \mathrm{RBW}\right]^{1 / 2} $

(8)

式中，RBW=(f_h -f₁)/f_c为相对宽度。

3 RMS值计算及PDF图绘制

利用乌加河地震台、乌力吉地震台的观测数据，计算2个台站的背景噪声水平的速度均方根值、功率谱密度（PSD），通过得出的数据绘制各通道PSD值、PDF图。

3.1 RMS值

选取2020年5月1—7日乌加河地震台、乌力吉地震台记录的波形数据，计算2个台的背景噪声均方根（RMS）平均值，计算结果见表 2。

3.2 台基噪声

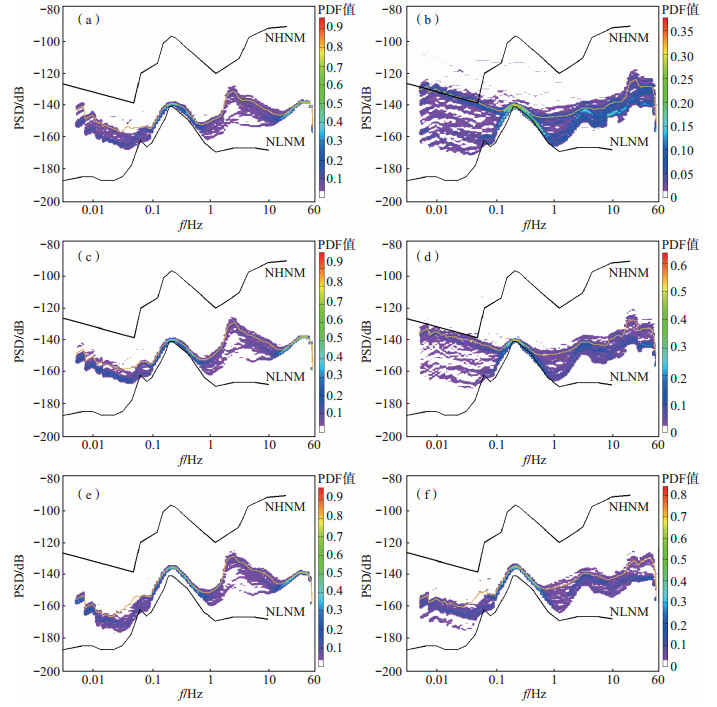
截取2020年5月1—7日乌加河地震台、乌力吉地震台的原始地震波形数据，运用PDF方法，不需要去除地震在内的突发事件及观测系统的瞬态变化、仪器毛刺等信号，直接计算相应台站的PSD值，通过计算出的PSD值绘制PDF图（图 2）。

由图 2可见，乌力吉地震台在低于0.1 Hz频段台基噪声曲线变化幅度较大，接近全球高噪声模型NHNM，其中，SN向已超过全球高噪声模型NHNM；乌加河地震台在低于0.1 Hz频段台基噪声曲线相对较平缓。但是，乌加河地震台在2—10 Hz频段的台基噪声曲线变化幅度较大，而乌力吉地震台在2—10 Hz频段曲线较平稳。

3.3 中午、凌晨2个不同时段台基噪声

选取乌加河地震台、乌力吉地震台9—13时与0—5时2个时段内波形数据，分析在其他外界环境不变的情况下，环境温度的变化对不同观测形式下台基噪声的影响。乌加河地震台地震计放置在由山体覆盖的山洞内，洞内全年恒温恒湿，受外界温度变化的影响较小；乌力吉地震台地震计放置在观测房内摆墩上，由于观测房结构简单，墙体较薄，不能起到较好的保温作用，故乌力吉地震台地震计受外界温度变化的影响较大。

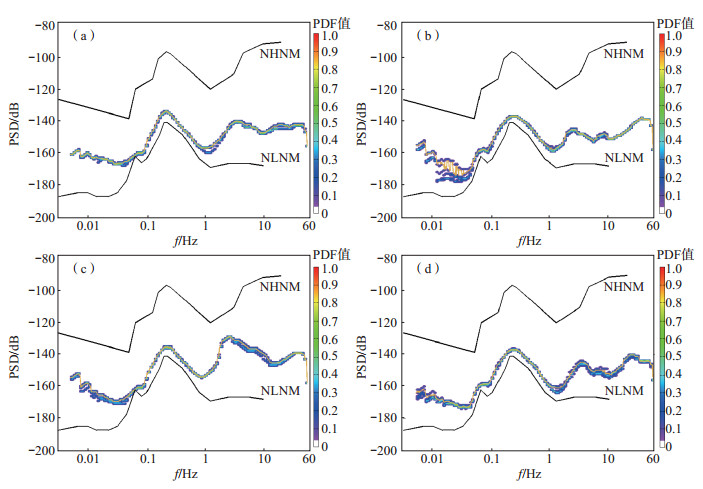
图 3为乌加河地震台、乌力吉地震台白天与夜间的台基噪声特性曲线。由图 3可见，温度的变化对地震计的影响明显。综合分析乌加河地震、乌力吉地震台的台基噪声特性曲线及台站环境可知，乌力吉地震台地震计受周围温度影响较大，这导致乌力吉地震台的台基噪声特性曲线在低于0.1 Hz的低频段内噪声曲线呈较大幅度的变化。

3.4 乌加河地震台、乌力吉地震台谷歌地图

为了充分了解不同环境因素对乌加河地震台、乌力吉地震台地震计台基噪声的影响，从谷歌地球上截取乌加河地震台、乌力吉地震台的谷歌地图（图 4），通过谷歌地图计算出乌加河地震台、乌力吉地震台距人类聚居区的直线距离，以间接地了解人为活动对台基噪声产生的影响。

对比乌加河地震台、乌力吉地震台三向2—10 Hz高频段台基噪声特性图（图 2），并结合谷歌地图（图 4）查看2个台2 km范围内的周围环境可知，乌加河地震台靠近村庄，人为干扰严重，这导致乌加河地震台的台基噪声特性曲线在2—10 Hz高频段呈现较大幅度变化；而乌力吉地震台距村庄较远，故2—10 Hz高频段噪声对其干扰较小，所以乌力吉地震台在2—10 Hz高频段台基噪声曲线较平稳。

4 结论

通过对比乌加河地震台、乌力吉地震台的波形数据功率谱概率密度谱，并考虑2个地震台所处的地理环境因素，得出以下结论。

乌力吉地震台的台基噪声主要包括人为噪声、微震噪声和由风、大气压、温度等因素引起的自然环境噪声，其中，乌力吉地震台地震计受到温度变化的影响较大，环境噪声对地震计的影响主要集中在低频段，这导致乌力吉地震台在低频段噪声曲线变化幅度较大；乌加河地震台地震计位于观测山洞内，洞内常年温度、气压变化较小，地震计受环境噪声的影响较小，人为噪声对地震计的影响主要集中在高频段，这导致乌加河地震台在高频段台基噪声曲线变化幅度较大。因此，在台站建设初期可通过改变洞体结构，以及使台站远离主要公路、村镇的方法降低观测中的背景噪声。