2) 中国西宁 810001 青海省地震局;
3) 中国乌鲁木齐 830011 新疆维吾尔自治区地震局
2) Qinghai Earthquake Agency, Xining 810001, China;
3) Earthquake Agency of Xinjiang Uygur Autonomous Region, Urumqi 830011, China
震后初期,地震现场救援是一项复杂、多任务、多兵种协同的工作,需要大量时间开展现场调查才能对震灾损失进行准确评估。地震灾害损失评估结果的快速获取,对于制定应急救援措施和实施救灾决策,具有重要的指导作用。因此,在地震灾害快速评估工作中,评估结果的精准性显得尤为重要。
地震灾害快速评估工作是指,地震灾害发生之后,快速估计地震成灾范围、人员伤亡和经济损失等相关工作(陈文凯等,2020)。此项工作的开展,不仅可为各级政府和应急管理部门地震应急指挥决策提供重要的信息服务,也可为地震应急救援与指挥决策提供重要的数据支撑平台(丁香等,2019)。其基本思路是:在地震发生时间、地点和震级确定后,开展地震现场调查前,利用震前当地人口、建筑、经济、环境等基础数据,按照地震烈度计算、伤亡估计、经济损失估计等数学和经验模型,估算烈度分布和震害损失。
影响地震灾害损失快速评估的因素主要有:地震发生时刻、震级、场地类型、烈度衰减关系、人员伤亡估计模型等(任静等,2020)。由于各因素之间存在非线性和离散性,评估与实际结果会存在差异。在现有研究条件下,如何克服上述因素的影响,进一步提高破坏性地震灾害损失快速评估的科学性、准确性和可靠性,是当前应急救援工作面临的挑战之一。
据中国地震台网中心测定,2021年5月22日青海省果洛藏族自治州玛多县发生MS 7.4地震(34.59°N,98.34°E),震源深度17 km(http://www.ceic.ac.cn)。此次地震造成19人受伤(https://www.mem.gov.cn/)。根据地震速报参数,震后即给出地震灾害损失快速评估结果:地震最高烈度达Ⅸ度(9度),可能造成个别人员死亡。为了探寻此次地震灾害损失快速评估与地震现场调查结果存在的偏差,本文拟从地震影响场分布、灾区人口分布、人员伤亡模型及其影响因素等进行对比分析,以便为提高地震灾害快速评估结果的准确性提供科学参考,为政府救援力量部署和抗震救灾阶段划分提供重要依据。
1 思路和方法选择不同的地震影响场烈度快速评估模型和不同的人员伤亡评估模型,从地震现场调查评估与所选影响场模型损失评估结果对比、地震影响场的不确定性分析、地震人员伤亡快速评估结果分析、各影响场模型下人员死亡模型损失计算结果对比、灾区人口分布特征对人员伤亡的影响等方面,综合分析各模型下地震快速评估与真实结果的偏差。在灾害损失快速评估中,公里网格人口数据集是基于受多种因素影响的数据集(人口数据、行政区划数据、DEM等地形数据等),数据集选自“南北地震带大震极灾区速判及关键技术研究——地震带区域基础数据更新与数据转换”项目成果。
2 地震影响场的快速评估 2.1 地震影响场烈度快速评估模型选择地震灾害损失主要受地震影响场的影响,地震影响场受则受地震强度(震级大小)、地震动衰减等因素的影响,而地震动参数确定的基础和前提是烈度衰减关系(任静等,2021)。为了分析地震灾害损失评估结果的精准性,采用地震现场调查烈度图与3种地震影响场评估模型的烈度分布进行分析,各评估模型见表 1。
| 表 1 地震现场评估与地震影响场评估模型 Table 1 On-site evaluation results and four types of earthquake-influenced field evaluation models |
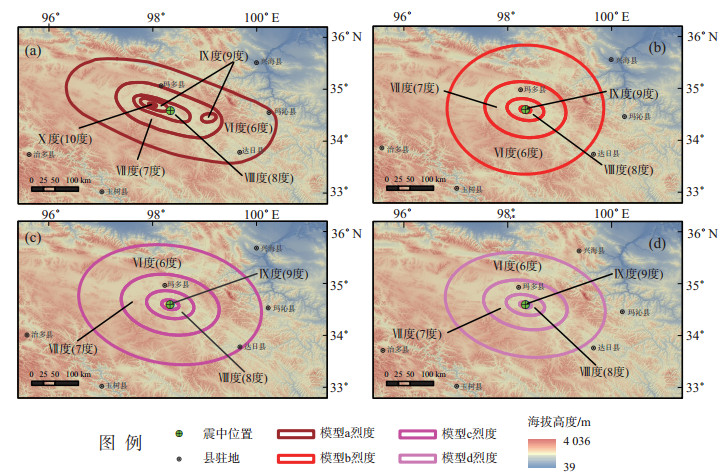
模型a——现场调查烈度图:采用地震现场调查评定结果的地震烈度图[图 1(a)],是基于实际震害调查(https://www.cea.gov.cn/)结果,即通过对震区进行抽样调查,并参考震区的构造背景、震源机制解、强震动观测记录等因素而确定的。
|
图 1 地震现场评估结果(模型a)与3种评估模型的地震影响场分布 (a)模型a;(b)模型b;(c)模型c;(d)模型d Fig.1 Distribution maps of seismic influence field based on on-site assessment results (model a) and three assessment models |
模型b——中国分区地震动衰减关系模型:采用青海省快速评估影响场[图 1(b)]的地震烈度衰减模型,其中涉及的地震参数为中国地震台网中心正式速报三要素结果:震级7.4,震中位置(34.59°N,98.34°E),震源深度17 km;震源破裂方向由震中附近活动构造方向而确定;模型烈度衰减关系选取汪素云等(2000)给出的中国分区地震动衰减关系(中国西部),其中
| $ {{I_{\rm{a}}} = 6.4580 + 1.2746M - 4.4700\lg \left({{R_{\rm{a}}} + 25.000} \right)} $ | (1) |
| $ {{I_{\rm{b}}} = 2.019 + 1.398M - 2.943\lg \left({{R_{\rm{b}}} + 8.000} \right)} $ | (2) |
式中,Ia、Ib为椭圆衰减模型沿长、短轴方向的烈度值,Ra、Rb为长、短轴半径(单位km),M为震级。
模型c——青海省烈度衰减关系模型:采用青海省快速评估影响场[图 1(c)]的地震烈度衰减模型,其中地震参数及震源破裂方向同模型b;模型选择评估系统中现存烈度衰减关系(评估系统),其中
| $ {{I_{\rm{a}}} = 6.2513 + 1.3046M - 4.4496\lg \left({{R_{\rm{a}}} + 25} \right)} $ | (3) |
| $ {{I_{\rm{b}}} = 3.4575 + 1.3046M - 3.4264\lg \left({{R_{\rm{b}}} + 10} \right)} $ | (4) |
式中,Ia、Ib为椭圆衰减模型沿长、短轴方向的烈度值,Ra、Rb为长、短轴半径(单位km),M为震级。
模型d——地震灾害快速评估系统烈度衰减模型:采用青海省快速评估影响场[图 1(d)]的地震烈度衰减模型,其中地震参数及震源破裂方向同模型b;模型选取中国西部分区地震烈度衰减关系模型(新疆区)(肖亮等,2011),其中
| $ {{I_{\rm{a}}} = 5.6018 + 1.4347M - 4.4899\lg \left({{R_{\rm{a}}} + 25.000} \right)} $ | (3) |
| $ {{I_{\rm{b}}} = 3.6113 + 1.4347M - 3.8477\lg \left({{R_{\rm{b}}} + 13.000} \right)} $ | (4) |
式中,Ia、Ib为椭圆衰减模型沿长、短轴方向的烈度值,Ra、Rb为长、短轴半径(单位km),M为震级。
2.2 4种模型损失评估结果对比依据模型b、模型c、模型d烈度衰减关系模型,计算得到3种影响场评估结果,与模型a,即地震现场评估结果列于表 2,并根据表 2所示极震区烈度及相应烈度区长、短轴距离,测量得到4种模型烈度区面积,结果见表 3。
| 表 2 地震现场评估结果(模型a)与3种影响场评估的地震损失结果对比(长、短轴,单位km) Table 2 Comparison of the on-site evaluation results of the impact field of the earthquake (model a) and the earthquake loss evaluation results of the three impact field evaluation schemes (long and short axis, unit: km) |
| 表 3 地震现场评估结果(模型a)与3种影响场评估的地震损失结果对比(面积,单位km2) Table 3 Comparison of the on-site evaluation results of the impact field of the earthquake (model a) and the earthquake loss evaluation results of the three impact field evaluation schemes (area, unit: km2) |
由表 2、表 3可知,模型a(地震现场调查评定烈度图)极震区烈度达Ⅹ度,而据模型b、模型c、模型d估算的极震区烈度均为Ⅸ度(9度),且无模型a所展现的Ⅸ度(9度)异常区。将3种影响场评估模型与模型a进行对比,由表 2、表 3可见:Ⅸ度(9度)区长轴相差21—32 km,短轴相差在2—8 km,面积相差222—522 km2;Ⅷ度(8度)区长轴相差23—42 km,短轴相差8—30 km,面积相差128—1 069 km2;Ⅶ度(7度)区长轴相差21—52 km,短轴相差15—38 km,面积相差在374—2 896 km2;Ⅵ度(6度)区长轴相差54—104 km,短轴相差21—52 km,面积相差2 826—6 919 km2。
由上述结果可知,模型b、模型c、模型d对应各烈度区的长、短轴、面积,均与地震现场调查评定结果(模型a)存在偏差,究其原因是:地震烈度衰减关系受震源特性、深部构造、传播介质、场地条件、建筑物结构类型和居民点分布、地形等因素的影响(Ren et al,2021),在模型b、模型c、模型d中,烈度衰减关系均采用椭圆模型,涉及变量仅有烈度、震级、长短轴半径,且认为烈度随震中距呈对数关系衰减,未过多考虑更多影响因素。
2.3 地震影响场的不确定性分析20世纪90年代初,中国地震局组织开展历次破坏性地震震害调查、烈度评估、震害损评估等现场相关工作,调查资料真实反映了历史地震造成的破坏。针对地震影响场评估的不确定性,选取我国西部1900—2020年6.0≤M≤8.0地震烈度分布数据(数据来源真实可靠)(国家地震局地震灾害应急救援司,2010;国家地震局地震应急救援司, 2015a, 2015b),对所选烈度图进行精准配准和数字化,测出历史地震震例各烈度圈的实际烈度面积(任静等,2021)。
在1979年以前,我国大部分房屋未烈度设防。2004年起,国家开始实施并建设西部农居抗震安居工程。据此,将测量烈度圈面积数据按时段分为3组:第1组:1900—1978年数据;第2组:1979—2003年数据;第3组:2004—2020年数据(任静等,2020)。按不同分组,绘制1900—2020年中国西部地区震例震级—烈度区面积分布图,结果见图 2。

|
图 2 所选震例震级—烈度区面积关系 Fig.2 The magnitude-intensity area relationship of selected earthquakes |
图 2中绿点表示1900—1978年中国西部地区6.0≤MS≤8.0地震数据,棕色圆点表示中国西部地区1979—2003年6.0≤MS≤8.0地震数据,粉红色圆点表示2004—2020年中国西部地区6.0≤MS≤8.0地震数据,红色圆点表示2021年5月22日青海玛多MS 7.4地震。由图 2可知:6.0≤MS≤8.0地震最大烈度可达Ⅹ度,当震级相同时,同一烈度值下,烈度区面积最大可相差2个数量级,差距较大。分析认为,房屋、建筑物的抗震设防水平对各烈度圈面积大小有一定影响,但烈度区面积应还受到生命线工程的破坏程度、地震地质灾害等因素影响(任静等,2021)。
3 震灾中人员伤亡的快速评估 3.1 人员死亡评估模型选取人员伤亡评估模型要求需具备应用、实证及有效性的方便和快捷。目前,常用模型有基于地震参数和基于建筑物易损性的2种模型。此外,基于时间序列、神经网络方法和动态评价方法等模型,应用条件较复杂,实证和性能评价较困难(齐凤娇等,2019)。
人员死亡评估模型因来源不同,所采用的数学表达方式不同,适用的空间范围和时间段也不同。考虑到震后数据第一时间获取的难易程度以及人员伤亡评估的快速性需求,采用以下6种模型,对青海玛多MS 7.4地震灾害中造成的死亡人数进行重新估算,分析各个模型的适用范围及结果精度。
3.1.1 模型1刘金龙等(2012)以我国1990—2006年造成人员伤亡的破坏性地震为例,以震中烈度为主要参数,以震级和人口密度为辅助参数,建立修正的人员伤亡预测模型,文中简称刘金龙模型。模型如下
| $ {D = {\alpha _m}{\alpha _{{\rm{den }}}}{D_m} = {{\rm{e}}^{12.2{\alpha _m}{\alpha _{{\rm{den}}}}{{\rm{e}}^{ - {{(\ln ({\mathop{\rm lnt}\nolimits}) - 2.445)}^2}/{{0.3}^2}}}}}} $ | (5) |
| $ {{\alpha _m} = \frac{{{\rm{Mag}}}}{{0.533 {\rm{lnt}} - 3}}} $ | (6) |
| $ {{\alpha _{{\rm{den }}}} = 0.113\ln ({\rm{Den}}) + 0.443} $ | (7) |
式中,lnt为震中烈度,Mag为震级,αm为震级修正系数,αden为人口密度修正系数,D为死亡人数。
此次玛多MS 7.4地震震中所在地青海省果洛州玛多县人口总数:14 490人,面积2.52 km2。
3.1.2 模型2P.A.Page等(马玉宏等,2000)将发震时间划分为白天(08:00—18:00)和夜晚(08:01—7:59),以烈度、人口为主要参数,建立人员评估模型,文中简称P.A.Page模型,公式如下
| $ \ln N_{\text {白 }}=-22.73+10.6 \ln I+0.34 \ln \rho $ | (8) |
| $ \ln N_{\text {夜 }}=-11.35+5.77 \ln I+0.36 \ln \rho $ | (9) |
| $ \ln N_{\text {夜 }} / N_{\text {白 }}=11.38-4.83 \ln I $ | (10) |
式中,N白、N夜分别为白天、夜间发震时的死亡人数,ρ为人口密度,I为烈度。
3.1.3 模型3肖光先等(1991)考虑了不同烈度区的烈度、人口密度对死亡人数的影响,分烈度区估算地震死亡人数模型,文中简称肖光先模型,公式如下
| $ {\ln {R_{{{\rm{D}}_j}}} = - 44.365 + 7.516{I_j} - 0.329I_j^2} $ | (11) |
| $ {\ln {R_{{{\rm{D}}_j}}} = - 44.466 + 14.331{I_j} + 0.96\ln \rho } $ | (12) |
| $ {N_{\rm{D}}} = \sum\limits_{I = 6}^{{I_{\max }}} {\left({{A_j} - {A_{j + 1}}} \right)} \rho \times {R_{{{\rm{D}}_j}}} $ | (13) |
式中,RDj表示烈度为Ij时每单位建筑面积平均死亡率,ρ为人口密度,ND为死亡数,Aj表示I≥Ij的面积。
3.1.4 模型4李雯等(2016)以1966—2016年中国大陆地震灾害生命损失数据为研究对象,以人口密度分组(表 4)为依据,选取震中烈度、震区面积(Ⅵ度及以上)、震中烈度与抗震设防烈度之差作为参数建立模型,文中简称李雯模型,公式如下
| $ D=\mathrm{e}^{b_{0}+b_{1} I+b_{2} S+b_{3} \Delta I} $ | (14) |
式中,D为地震死亡人数,I为震中烈度,S为震区面积,ΔI为震中烈度与抗震设防烈度之差,b0、b1、b2、b3为回归系数。
| 表 4 中国西北地区人口密度分组 Table 4 Groups of population density in Northwest China |
Chen等(2005)选取国内1980—2000年的震例数据,将发震时间按白天(7:00—19:00)、夜晚(19:00—7:00)划分,建立人员死亡数与烈度的经验公式,文中简称陈棋福模型,公式如下
| $ \lg N_{\text {日 }}=32.704 \lg I+0.689 \lg D-29.786 $ | (15) |
| $ \lg N_{\text {夜 }}=19.795 \lg I+0.292 \lg D-17.047 $ | (16) |
式中:N日、N夜分别为白天、夜晚地震发生时的死亡人数,I为地震烈度,D为人口密度。
3.1.6 模型6陈尧(2015)基于震级、震中烈度建立地震人员伤亡快速评估模型,文中简称陈尧模型,公式如下
| $ {D = {f_\rho } \cdot {D^\prime } = 9.6 \times {{10}^{ - 11}} \times (0.00592\rho + 0.1714){{\rm{e}}^{4.19M}}} $ | (17) |
| $ {D = {f_\rho } \cdot {f_t} \cdot {D_m} = {f_t} \cdot (0.00592\rho + 0.1714){{\rm{e}}^{\left({0.1938{I^2} - 0.53791 - 5.304} \right)}}} $ | (18) |
式中,D为评估的地震死亡人数,D′为据震级拟合的地震死亡人数,Dm为据震中烈度拟合的地震死亡人数均值,fρ为人口密度修正系数,ft为发震时间修正系数,M为震级,I为震中烈度,ρ为震区人口密度。陈尧(2015)给出不同烈度下ft取值结果见表 5(表中修正系数涉及烈度最高为Ⅸ度,故计算模型a时,选取Ⅸ度系数)。
| 表 5 发震时间修正系数 Table 5 Origin time correction factors |
此次玛多MS 7.4地震未造成人员死亡,依据上述6种人员死亡评估模型,分别计算在4种地震影响场模型(模型a、模型b、模型c、模型d)下的人员死亡数,结果见表 6。
| 表 6 6种死亡模型评估结果对比 Table 6 Comparison of evaluation results of six casualty models |
由表 6可知:①使用不同人口死亡模型估算,在地震影响场模型a下死亡人数最多,而其他影响场模型下所得死亡人数相同。究其原因是,模型a为地震现场评估结果,地震烈度高达Ⅹ度,而模型b、c、d最高烈度为Ⅸ度,极震区烈度不同,故导致所得死亡人数出现偏差;②在不同地震影响场模型下,利用P.A.Page模型估算的死亡人数,与实际调查结果偏差较小。
除上述人员死亡模型外,根据研究角度的不同,仍有诸多评估方法,如:基于宏观经济指标的人员伤亡评估方法、人员伤亡指数与状态及其动态评估法等。由于各死亡模型所用震害数据与采用的拟合参数各不相同,且震害所致人员伤亡因素颇多,故评估值与实际死亡人数必然存在偏差。
3.3 灾区人口分布特征对人员伤亡的影响采用“南北地震带大震极灾区速判及关键技术研究——地震带区域基础数据更新与数据模式转换”项目所得人口公里格网数据,应用GIS软件,计算不同地震影响场模型下青海玛多MS 7.4地震灾区各烈度区人口分布数,结果表 7。
| 表 7 各影响场模型下不同烈度区人口数估算结果 Table 7 Estimation results of population in different intensity zones under the influence field models |
地震现场评估结果(模型a)为此次玛多MS 7.4地震勘探现场真实烈度区,各烈度区范围如下:Ⅵ度(6度)区涉及青海省3个市州7个县32个乡镇,四川省1个市州1个县4个乡;Ⅷ度(8度)区涉及青海省果洛藏族自治州玛多县查理镇、黄河乡、扎陵湖乡、花石峡镇;Ⅸ度(9度)区涉及果洛藏族自治州玛多查理镇和黄河乡;Ⅸ度(9度)区有一个异常区,涉及青海省果洛藏族自治州玛沁县大武镇、优云乡;Ⅹ度(10度)区涉及果洛藏族自治州玛多查理镇(https://www.mem.gov.cn/)。
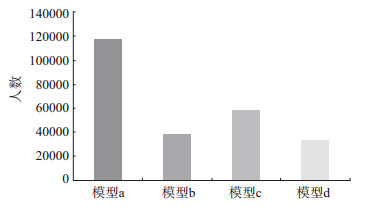
模型b、模型c、模型d烈度衰减关系不同,对于此次地震的烈度区估计范围也不同。利用3种模型估算人口公里格网人数,与模型a所得结果相差5.890 2—8.412 2万人,结果见图 3。
|
图 3 各影响场模型下人口数 Fig.3 Population under each intensity model |
4种影响场评估模型烈度区范围不同,人口分布估算结果不同。在以上6种不同类型人员伤亡模型,即刘金龙模型、P.A.Page模型、肖光先模型、李雯模型、陈棋福模型和陈尧模型中,涉及参数有烈度、各烈度圈面积、人口密度、设防烈度等,因参数各不相同,造成基于模型a、模型b、模型c、模型d的人员伤亡估算结果与地震所致真实死亡数据存在偏差。综上所述,地震灾害损失评估受灾区人口分布的影响,准确的人口数据和地震影响场对震灾害损失评估结果的精准性具有重要影响。
3.4 其他因素对此次地震中人员伤亡的影响在此次青海玛多MS 7.4地震中,实际死亡人数为0,远小于利用模型估算结果,这是因为,除上述影响因素外,尚有其他因素产生影响,如:房屋抗震性能、次生灾害等。
3.4.1 房屋抗震性能的影响在地震灾害中,房屋抗震性能是造成人员伤亡的主要因素之一。据统计,约75%的人员死亡由建筑物破坏和倒塌所致。地区抗震设防水平及设防烈度越高,建筑物的修建要求和标准越严格,抗震性能就越好,震后房屋倒塌和破坏数越少,人员伤亡就越小,反之,人员伤亡就越大(马玉宏等,2000)。提高房屋抗震性能是减小人员伤亡的重要手段之一。
此次地震仅造成震中附近个别土木结构、砖木结构房屋出现倒塌、破坏,部分砖混及框架结构楼梯间及填充墙出现开裂现象。据调查,房屋损失主要是因为牧区老旧建筑多未经抗震设计所致,而多数房屋基本完好,则是因为房屋设施加固工程项目的实施,提升了房屋抗震设防能力(殷翔等,2021)。
本次地震的一个突出特点是灾情重、伤亡轻,原因是该地区抗震设防烈度为8度,实施脱贫攻坚、农牧区定居点建设后,建筑物抗震能力显著提升,倒塌房屋占比小,加之人口密度小,进一步减少了人员伤亡。但是,建筑设施受损仍较严重,特别是道路、桥梁等基础设施,在此次地震中受损程度较大。若此次地震发生在人口密集区域,人员伤亡占比可能较大,建议加大全国各地房屋设施加固工程的实施力度,提升抗震设防能力。
3.4.2 次生灾害影响地震次生灾害是强烈震动发生后,以工程结构和自然环境破坏为导因而引起的一系列灾害,如火灾、爆炸、泥石流、滑坡等(吴微微,2013)。在破坏性地震作用下,除建、构筑物倒塌和破坏直接导致人员伤亡外,还经常伴随次生灾害的发生而造成人员伤亡。
受此次玛多地震影响,在震后6个调查点中,次生灾害主要表现为滑坡、地面裂缝、塌陷及喷砂冒水现象。其中:喷砂冒水现象广泛,遍布Ⅶ度烈度区内;地表裂缝达上千条,其总体走向为NW280°,且连续性较好,表明均由此次地震引起,而非滑坡、冻土开裂等其他原因所致(李鑫等,2021)。此次地震未造成人员死亡,但在利用死亡模型进行估算时,考虑次生地质灾害因素的伤亡模型,会对震中烈度较大评估值结果进行提升,从而造成数值偏大。
3.4.3 其他影响除上述因素外,影响地震灾害人员伤亡的因素还有:临震前震的影响、地震预警作用、地形地貌、公众自救互救能力、地质构造、区域救援能力、建筑物结构构件和内部设施情况、人员作业方式、地震时人员所处的周围囤陷环境等(马玉宏等,2000)。
总之,地震灾害中人员死亡评估是系统而复杂的工作,死亡人数是致灾因子、孕灾环境、承灾体等多因子耦合的结果。
4 结论与讨论在进行地震灾害快速评估时,选取模型评估与实际所得结果会有一定偏差,可能是受到地震震级、极震区烈度估计、烈度衰减关系模型、人员伤亡评估模型等影响所致,因为以上要素本身均存在随机性。
针对2021年5月22日青海玛多MS 7.4地震,选取不同地震影响场烈度快速评估模型进行估计,与真实影响场结果进行对比,根据我国西部地区烈度区面积进行地震影响场的不确定性分析;而后选取不同的人员伤亡评估模型,对比分析不同影响场模型下人员伤亡快速评估结果,并探讨人口分布特征等,结果显示:①地震影响场具有明显的区域特征,目前灾害损失快速评估采用模型c,相比国内其他模型(模型b、模型d),在评估青海省某具体区域地震影响场时更具合理性;②地震中人员死亡评估是系统而复杂的工作,死亡人数是致灾因子、孕灾环境、承灾体等多因子耦合的结果,由于青海省地区孕灾环境和承灾体时空差异大,目前人员死亡评估方法存在一定局限性和适用范围。
伴随着新时代算法的精进和仪器测量精准性的加强,震源破裂过程和震源深度反演的精准性不断提高,在地震烈度衰减关系和地震影响场方向的判定过程中,综合考虑震源机制解、发震构造环境、余震序列等因素,可进一步提高地震影响场评估的精准性。应用人口公里格网和房屋建筑易损性矩阵等数据开展相关研究,若启用“第一次国情普查建筑数据”,必将大幅提升评估结果的精准度。“第一次国情普查建筑数据”为真实的建筑数据,精准度高,但目前仍为涉密数据,尚未投入相关研究。此外,人员死亡评估受震区地形地貌、次生地质灾害、临震预警、区域救援能力、公众自救互救能力等因素的影响,鉴于评估系统的复杂性,应对地震损失快速评估结果进行专家干预,以确保结果的精准性。
陈文凯, 周中红, 张灿, 等. 新一代区域地震灾害快速评估系统设计与实现——以甘肃省为例[J]. 地震工程学报, 2020, 42(6): 1 683-1 692. |
陈尧. 破坏性地震人员伤亡快速评估方法研究[D]. 哈尔滨: 中国地震局工程力学研究所, 2015.
|
丁香, 王晓青, 袁小祥, 等. 2017年5月11日新疆塔什库尔干5.5级地震生命损失评估对比分析[J]. 震灾防御技术, 2019, 14(2): 431-437. |
国家地震局震灾应急救援司. 1966-1989年中国大陆地震灾害损失评估汇编[M]. 北京: 地震出版社, 2015a.
|
国家地震局震灾应急救援司. 2001-2005年中国大陆地震灾害损失评估汇编[M]. 北京: 地震出版社, 2010.
|
国家地震局震灾应急救援司. 2006-2010年中国大陆地震灾害损失评估汇编[M]. 北京: 地震出版社, 2015b.
|
李雯, 陈文凯, 周中红, 等. 中国典型区域地震灾害生命易损性模型适用性评价[J]. 北京师范大学学报, 2019, 55(2): 284-290. |
李鑫, 殷翔, 姚生海, 等. 青海玛多7.4级地震重灾区房屋震灾调查及分析[J]. 地震工程学报, 2021, 43(4): 896-902. DOI:10.3969/j.issn.1000-0844.2021.04.896 |
刘金龙, 林均岐. 基于震中烈度的地震人员伤亡评估方法研究[J]. 自然灾害学报, 2012, 21(5): 113-119. |
马玉宏, 谢礼立. 地震人员伤亡估算方法研究[J]. 地震工程与工程振动, 2000, 20(4): 140-147. |
马玉宏, 谢礼立. 关于地震人员伤亡因素的探讨[J]. 自然灾害学报, 2000, 9(3): 84-88. |
亓凤娇, 苏鹤军, 陈文凯, 等. 地震灾害人员死亡评估模型对比——以甘肃省中强震为例[J]. 华北地震科学, 2021, 39(1): 9-17. |
任静, 阿里木江·亚力昆, 李志强, 等. 2020年1月19日新疆伽师6.4级地震灾害损失快速评估精准性分析[J]. 震灾防御技术, 2020, 15(2): 349-358. |
任静, 张方浩, 李志强, 等. 2021年5月21日云南漾濞6.4级地震灾害损失快速评估结果分析[J]. 震灾防御技术, 2021, 16(3): 454-462. |
汪素云, 俞言祥, 高阿甲, 等. 中国分区地震动衰减关系的确定[J]. 中国地震, 2000, 16(2): 99-106. |
吴微微. 从汶川和芦山地震浅析四川地震次生地质灾害的特点及减灾对策[J]. 震灾防御技术, 2013, 8(4): 434-439. |
肖光先. 震后灾害损失快速评估[J]. 灾害学, 1991, 6(4): 12-17. |
肖亮, 俞言祥. 中国西部地区地震烈度衰减关系[J]. 震灾防御技术, 2011, 6(4): 358-371. |
殷翔, 李鑫, 马震, 等. 青海玛多MS 7.4地震震害特点分析[J]. 地震工程学报, 2021, 43(4): 868-875. |
中国地震局监测预报司. 1996-2000年中国大陆地震灾害损失评估汇编[M]. 北京: 地震出版社, 2001.
|
Chen Q F, Mi H L, Huang J. A simplified approach to earthquake risk in mainland China[J]. Pure and Applied Geophysics, 2005, 162(6/7): 1 255-1 269. |
Ren J, Li Z Q, Huang S T, et al. Comparative study on the deviation characteristics of post-earthquake intensity evaluation based on two intensity attenuation relationship models[J]. Earthquake Research Advances, 2021, 1(2): 7-14. |
 2022, Vol. 43
2022, Vol. 43

