0 引言

大地震除产生涉及地球局部运动的体波和面波外，还能激发全球规模、维持数天的地球自由振荡，属地球简正模运动（孙和平等，2017）。对地球自由振荡信号的观测与研究是认识地球内部大尺度结构的重要手段（严珍珍等，2008），通过将自由振荡频率观测值和不同地球模型下的理论频率值进行对比，可以对地球模型进行检验和修正，进而研究地球内部结构。此外，由大地震引起的基频地球自由振荡振幅大小与发震断裂的破裂过程及地震矩密切相关，可用于研究大地震的发震过程及机制（Joseph et al，1998；Park et al，2005）。地球自由振荡存在环型振荡和球型振荡2种基本振型，状态良好的重力仪适合观测球型自由振荡（Garland，2003）。

gPhone重力仪是目前监测地表垂直形变和重力场变化的精密仪器之一，具有动态线性测量范围宽及噪声水平低的特点，可检测几秒到几年周期尺度的地球重力场信号，具备检测球型地球自由振荡的观测能力。诸多研究表明，利用gPhone重力仪检测地球自由振荡信息在实际观测中是可靠的，如：刘正华等（2011）利用日本M_W 9.0强震检定4个台站gPhone重力仪探测地球自由振荡的有效性，并与超导重力仪SG的观测值以及HB1模型的理论值进行对比，结果吻合较好；周江林等（2016）利用北京地震台gPhone重力仪观测资料，检测到尼泊尔M_S 8.1地震激发的地球球型自由振荡周期，证实了gPhone重力仪能有效检测地球自由振荡信号；万禹等（2019）利用襄樊地震台gPhone重力仪观测数据，检测到2017年墨西哥M_W 8.2地震激发的自由振荡信息，与PREM模型的理论值基本相符。

泉州基准地震台（下文简称泉州台）gPhone重力仪于2015年12月安装，观测山洞覆盖层厚52.5—95.5 m，进深达190 m，从洞口到山洞最内段的重力观测区安装有9道不锈钢隔门，可有效防止空气对流，重力观测区年温度变化量小于0.5℃，日温度变化量小于0.05℃，观测环境良好，观测资料稳定、可靠、连续。2021年7月29日美国阿拉斯加州以南海域发生M_S 8.1地震（下文简称美国海域M_S 8.1地震），泉州台gPhone重力仪清晰记录到此次地震，为检测地球球型自由振荡提供了良好的数据基础。本文基于泉州台gPhone重力仪噪声水平特点，讨论预处理对自由振荡信息提取的影响，分析利用重力仪原始观测数据直接检测此次M_S 8.1地震自由振荡信息的可行性。

1 仪器噪声水平

重力观测数据中包含固体潮、气压、地球极移、仪器漂移、地震和海潮等大量信息（万禹等，2019），表达式如下

$ \operatorname{Obs}(t)=\operatorname{Tide}(t)+\alpha P(t)+D(t)+\operatorname{Res}(t) $

(1)

式中，Obs(t)为原始观测数据，Tide(t)为固体潮影响，α为大气重力导纳值，P(t)为台站气压观测值，D(t)为仪器的零点漂移，Res(t)为包括重力信号、环境噪声背景和其他未知干扰的重力残差及非潮汐分量，在无干扰情况下为白噪声序列（陈晓东等，2002）。

利用国际地球潮汐研究中心推荐的Tsoft软件（Vauterin，1998），对泉州台gPhone重力仪观测数据进行预处理，采用WDD潮汐模型，计算并扣除观测点的固体潮理论影响值Tide(t)。气压变化对重力观测的影响比较复杂，但对于台站重力观测而言，可以简单地用气压变化值P(t)乘以一个大气导纳常数α作为重力观测的气压改正。大气导纳常数α一般约为-0.3×10^-8 m·s^-2/hPa（徐建桥等，1999），而由气压引起的重力变化幅度一般在（2—3）×10^-8 m·s^-2范围内，故气压改正仅表现出较小变化，文中采用的气压改正值为-0.32×10^-8 m·s^-2/hPa；与超导重力仪漂移率极低不同，gPhone重力仪采用零长弹簧系统，需利用Tsoft软件中的九阶多项式拟合方法去除仪器漂移。

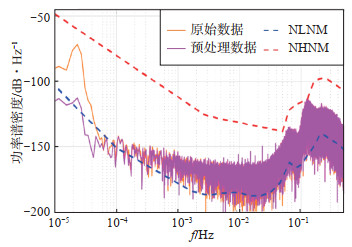
选择基本无震或人为干扰时段的原始观测数据Obs(t)和预处理数据Res(t)（剔除固体潮、气压影响以及漂移），计算泉州台gPhone重力仪噪声水平，结果见图 1，可见原始数据和预处理数据噪声水平均低于全球高噪声模型，部分频段低于全球低噪声模型，说明泉州台gPhone重力仪噪声水平良好，具备记录自由振荡信息的能力。

由图 1可见：在(1.0—6.0)×10^-5 Hz频段，预处理数据Res(t)比原始观测数据Obs(t)的噪声明显降低，特别在半日波处（图 1中频率约2.315×10^-5 Hz处），说明预处理数据去除了固体潮、漂移和气压影响，使得低频段噪声水平得到改善；在6×10^-5—0.5 Hz频段，预处理数据和原始数据的噪声水平无明显差别，表明泉州台重力观测数据受固体潮影响较大，气压干扰和仪器漂移对数据的影响较小；在地球自由振荡信号分布的主要频段(0.2—8)×10^-3 Hz内，原始数据和预处理数据噪声水平分布无显著差别。

2 资料处理方法

泉州台gPhone重力仪在低频段的低噪声水平有利于记录地球自由振荡信息。在正常工作状态下，该重力仪在福建省同类仪器中漂移量最小，2021年1月至7月28日（美国海域M_S 8.1地震发生前一天），其总漂移量约8 μGal。据前文分析，若该重力仪运行状态良好，是否采用预处理数据，对于提取地球自由振荡信息影响不大。由于大地震激发的地球振荡能持续数天时间，此次地震发震时刻为北京时间7月29日14:15:46，因此选用北京时间2021年7月29日14:00—8月3日14:00共120 h的原始秒采样数据进行分析。

采用功率谱密度估计方法获取数据的球型自由振荡频率。设信号x的自相关函数为R_n，定义信号x的功率谱密度值S_k为R_n的Fourier变换（万永革等，2012），则有

$ S_{k}=\sum_{n=0}^{N-1} R_{n} \mathrm{e}^{-i \frac{2 \pi n k}{N}} \quad k=0, 1, 2, \ldots, N-1 $

(2)

$ R_{n}=\frac{1}{N} \sum_{j=0}^{N-1} x_{j} x_{j+n} \quad n=-(N-2), -(N-1), \cdots, -1, 0, 1, \cdots, (N-2), (N-1) $

(3)

式中，x取重力原始秒采样数据序列，N为x的数目，n、k分别为R_n和S_k的序列号，j为求和参数。为了消除数据不能无限长而必须加窗造成的对功率谱密度估计的影响，采用Hanning窗来抑制旁瓣，突出主瓣（万永革等，2012）。

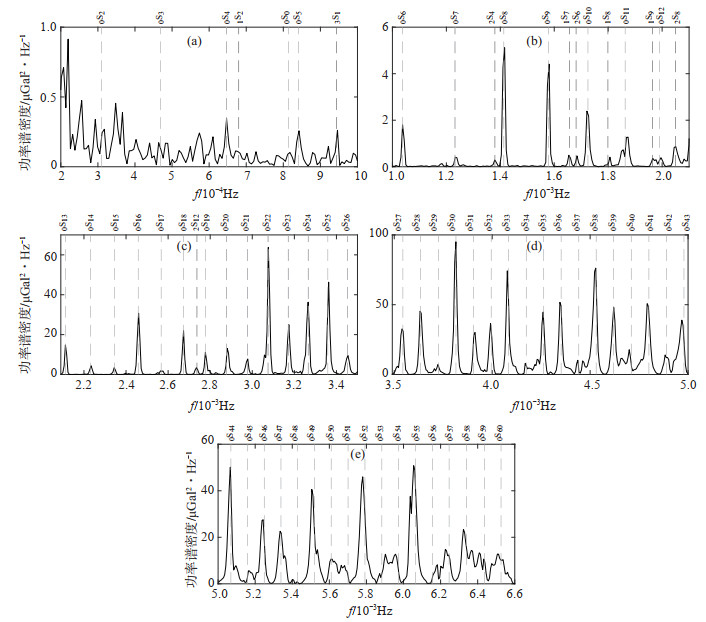
3 自由振荡信号提取

选取泉州台gPhone重力仪记录的美国海域M_S 8.1地震原始观测数据，采用功率谱密度估计方法，提取地球自由振荡信号，并与PREM模型（Wang et al，2012）的理论自由振荡周期进行对比。为将所检测地球自由振荡信号清晰分辨并标识出来，依据地球自由振荡信号在频域的分布特点，分(0.2—1.0)×10^-3 Hz、(1.0—2.1)×10^-3 Hz、(2.1—3.5)×10^-3 Hz、(3.5—5.0)×10^-3 Hz、(5.0—6.6)×10^-3 Hz五个频段进行功率谱密度估计，结果见图 2。图中虚线上方的数字和字母表示PREM模型下的理论自由振荡振型，红色虚线表示基频振型的理论频率值，蓝色虚线表示谐频振型的理论频率值，尖峰（凸起）所对应的频率值即为记录的自由振荡频率值。

图 2(a)给出最低频段(0.2—1.0)×10^-3 Hz范围内重力观测数据功率谱密度与PREM模型给出的理论球型自由振荡频率值的对应情况，可见在该频段能记录到₀S₄、₀S₅和₃S₁振型，₀S₂、₀S₃和₀S₀振型的功率谱密度值虽然有相应峰值对应，但与仪器自身噪声不能被较好地区分开，可能未满足激发条件，需能量更大的地震才能将其激发出来，同时₀S₂、₀S₃振型难以观测的原因在于2种振型存在谱线分裂现象，能量被分散在邻近几个频率，故在功率谱上较难观测（万永革等，2007）。

图 2(b)和图 2(c)给出(1.0—3.5)×10^-3 Hz范围内重力观测数据功率谱密度与PREM模型给出的理论球型振荡频率值的对应情况，可见随着频率的增大，自由振荡信号与噪声的信噪比更高，多数记录的自由振荡信号强度明显高于仪器自身噪声。在该频段，可识别的基频振型为₀S₆—₀S₂₆，但部分振型与PREM模型理论值有所偏离，其中₀S₁₁振型偏差最大，偏差率0.32%（观测值为1.868×10^-3 Hz，理论值为1.862×10^-3 Hz），而₀S₁₂振型偏差次之，偏差率0.30%；可识别的谐频振型是₂S₄、₁S₇、₂S₆、₁S₈、₁S₉、₂S₈、₂S₁₂，其中₁S₈振型偏差最大，偏差率0.44%（观测值为1.807×10^-3 Hz，理论值为1.799×10^-3 Hz）。由图 2可见，在(1.0—3.5)×10^-3 Hz内偏差率最大的₀S₁₁、₁S₈和₀S₁₂振型相邻，其中₀S₁₁在谱峰上表现为“分化”成2个振型，可能是3个振型所在频段(1.8—2.0)×10^-3 Hz内存在一些环境干扰，或者与仪器性能有关。除₀S₁₁和₀S₁₂振型外，在该频段内其他基频振型识别均较为理想，94%的振型偏差绝对值小于0.2%，偏差存在可能与地球介质的横向不均匀性或各向异性有关。

图 2(d)给出(3.5—5.0)×10^-3 Hz范围内重力观测数据功率谱密度与PREM模型给出的理论球型振荡频率值的对应情况，可见该频段噪声水平虽然比(1.0—3.5)×10^-3 Hz频段有所增大，但仍可检测到₀S₂₇—₀S₄₃振型，且88%的振型偏差绝对值小于0.2%。

图 2(e)给出(5.0—6.6)×10^-3 Hz范围内重力观测数据功率谱密度与PREM模型给出的理论球型振荡频率值的对应情况，由于频率越高，自由振荡能量衰减越快，且长时间序列观测数据对高频自由振荡信号的抑制效应（刘正华等，2011），造成₀S₄₄—₀S₆₀振型的观测值信噪比相对图 2(d)更低，部分振型的观测值与PREM模型理论值偏离增大，个别振型不能清晰分辨。

将各自由振荡振型的实际观测值与PREM模型理论值进行偏差统计，结果见表 1。

由表 1可见，大部分振型的观测值与理论值偏差绝对值在0.2%以内，总体平均偏差绝对值在0.15%以内，说明对基频振型₀S₄—₀S₆₀以及谐频振型₁S₃、₂S₄、₁S₇、₂S₆、₁S₈、₁S₉、₂S₈、₂S₁₂的检测结果与PREM模型理论值基本一致。结合图 2可知，实际观测值与理论值吻合较好，表明使用泉州台gPhone重力仪记录的原始数据，可有效检测美国海域M_S 8.1地震激发的地球自由振荡信号。

4 结论

泉州台gPhone重力仪记录到2021年7月29日美国阿拉斯加州以南海域M_S 8.1地震，分析利用原始数据检测该地震激发的地球自由振荡信号的可能性，得到以下几点认识：

（1）利用泉州台gPhone重力仪原始数据，成功检测到美国阿拉斯加州以南海域M_S 8.1地震激发的自由振荡信息。这是因为，对数据影响较大的固体潮与自由振荡研究频段不同，且地震发生时段受气压及仪器漂移影响较小。

（2）利用功率谱密度估计方法，检测到₀S₀—S₆₀基频振型以及部分谐频振型，结果与地球初步参考模型（PREM）的理论自由振荡频率吻合较好，既反映了泉州台gPhone重力仪运行状态良好，也表明了研究方法的正确性。

（3）₀S₂、₀S₃和₀S₀振型识别不清，主要原因可能是未满足激发条件，需更大能量才能将其激发出来，同时₀S₂、₀S₃振型存在谱线分裂现象，能量被分散在邻近几个频率。因此，有待进一步积累更大震级的震例来分析验证。

（4）部分振型观测值与理论值存在偏差，与地球介质的横向不均匀性或各向异性有关，也可能与环境干扰或者仪器在低频段的性能有关。在利用自由振荡信息反演修正地球模型时应注意剔除一些干扰信息。