太阳和月亮的引潮力作用使海水质量重新分布,地表荷载随之发生变化,引起固体地球产生形变,进而对地表的GNSS测站位置产生影响,且影响程度与测站所处位置有关(孙和平等,2002;周江存等,2005)。Baker等(1995)、Vey等(2002)、King等(2005)研究表明,海潮负荷对GNSS基准站基线解算有几个毫米精度的影响,沿海区域的海潮负荷对测站垂向位移的影响则可达到厘米级。自从Schwiderski于20世纪80年代构制第一个全球海潮模型以来,随着卫星测高等新技术的发展和应用,如NAO99.b、CSR4.0、FES2004等高精度、高分辨率的区域及全球海潮模型层出不穷。例如:FES2004海潮模型是根据动力模型、T/P卫星测高数据、ERS卫星测高数据、T/G潮高数据计算获得,该模型覆盖全球范围,格网分辨率为0.125°×0.125°。赵红等(2012)研究了不同海潮模型对单个不同位置的GPS测站定位的不同影响;张杰等(2013)分析了不同海潮模型对基线解的影响;雷锦韬等(2015)分析了海潮负荷对南极沿海地区基线解算带来的影响;刘洋洋等(2019)分析了海潮负荷对不同地区GPS测站的解算影响;翟丽娜等(2021)分析了海潮负荷对重力固体潮产生的影响。但上述文献大多围绕海潮模型对不同GNSS站点数据解算的影响展开分析,而未分析不同海潮模型的在中国范围内的不同影响,缺少对中国大陆构造环境监测网络(以下简称陆态网络)GNSS站点海潮模型的影响分析;同时,上述研究并未综合分析海潮负荷在整个GNSS基准站数据解算中的影响,选取指标仅包含基线或坐标结果。
本文选取2018年陆态网络GNSS基准站部分均匀分布站点,选用不同海潮模型分别参与数据解算,以基线解、坐标结果、站点时间序列等为指标,分析其所带来的不同影响,为选取海潮模型解算陆态网络GNSS数据提供参考。
1 数据选取及解算设置选取2018年陆态网络GNSS基准站及中国周边IGS站共48个测站数据,采用GAMIT/GLOBK软件,分别采用CSR4、FES2004、GOT00、NAO99b海潮模型,对所选站点GNSS数据进行解算,分别得到基线、定位、时间序列结果,以分析不同海潮模型对GNSS解算所带来的不同影响。所选站点分布见图 1(图中标注各站点代码),解算参数设置见表 1。
|
图 1 所选测站分布示意 Fig.1 Distribution of selected stations |
| 表 1 解算参数设置 Table 1 Main parameter settings of solution |
利用GAMIT/GLOBK软件,解算得到4种海潮模型影响下的基线、定位、时间序列结果,以单天解NRMS、基线相对精度、各基准站N、E、U精度、站点时间序列为指标,分析不同海潮模型对GNSS解算带来的不同影响。
2.1 基线结果对比标准化的均方根残差(normalized root mean square,NRMS)表示单时段基线解算值与其加权平均值的偏离程度。NRMS值是衡量基线解算质量的重要指标之一,计算公式为
| $ \mathrm{NRMS}=\sqrt{\frac{1}{N} \sum_{i=1}^{n} \frac{\left(Y_{i}-Y\right)^{2}}{\delta_{i}^{2}}} $ | (1) |
式中:N为测站数,Yi、Y分别代表基线解算值及其加权平均值,δi2即单位权中误差。一般认为NRMS值应小于0.3,但数值约0.25即可认为解算成功,且NRMS值越小,基线解算精度越高。若NRMS值> 0.5,则表明基线解算出现问题,需检查原因重新处理,可能原因是大周跳未去除、某解算参数设置有问题、解算模型设定有误等。
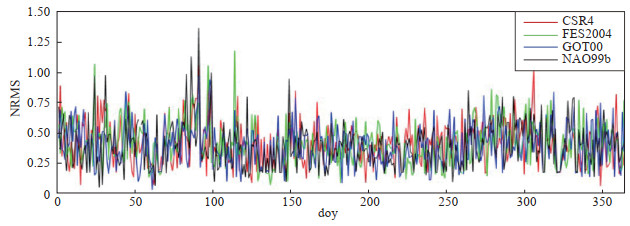
(1)NRMS值解算。由于解算结果是以天为单位的文件,故NRMS值存在于解算结果天文件中。利用CSR4、FES2004、GOT00、NAO99b四种海潮模型,绘制解算出的基准站单天解NRMS值变化图,提取每个结果文件NRMS值为纵坐标,年纪日为横坐标,绘制结果见图 2。由图 2可见,基于4种海潮模型解算的单天解NRMS值波动均较大,后期剔除不合格天数,各均值未超限定值。解算得到4种海潮模型的年均值,对应的单天解NRMS值分别为0.41、0.40、0.4、0.4,数值相差不大,表明基线解算合格。
|
图 2 基于不同海潮模型的单天解NRMS值 Fig.2 Single day baseline NRMS values calculated by different ocean tide models |
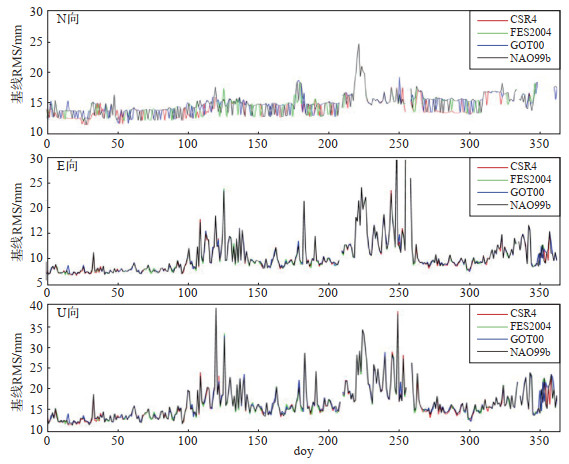
均方根误差(Root Mean Square,RMS)表明了观测值的精度,数值越小,精度越高。以云南施甸基准站(YNSD)与浙江温州基准站(ZJWZ)组成的基线YNSD-ZJWZ为例,提取单天结果文件中的基线N、E、U向RMS值精度,得到三方向年精度序列图及年均值,结果见图 3、表 2。
|
图 3 YNSD-ZJWZ基线N、E、U向精度年序列 Fig.3 Annual sequence diagram of N, E, U accuracy of YNSD-ZJWZ baseline |
| 表 2 YNSD-ZJWZ基线三方向解算精度年均值 Table 2 Annual mean of YNSD-ZJWZ baseline three directions |
由表 2可见,4种海潮模型的基线解精度基本一致,水平方向相差不大于1 mm,垂向相差不大于3 mm,其中CSR4模型三方向结果最佳,其余3种模型精度基本一致。综合年精度序列图(图 3)可知:4种海潮模型的基线精度解基本一致,CSR4模型的解算效果更佳。
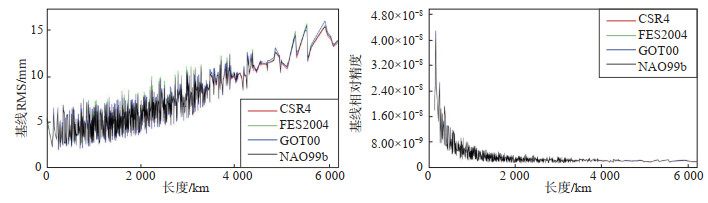
(2)基线精度与长度的关系。由于GAMIT软件对长基线的解算效果相对较好,为了在同一指标下对比海潮模型对不同长度基线解算结果的影响,挑选基线参与解算,并对比基线精度和相对精度,结果见图 4,图中横轴、纵轴分别表示基线长度、基线解算精度和相对精度。基线相对精度计算公式如下
| $ R=\frac{\text { NRMS }}{\text { length }} $ | (2) |
|
图 4 基线精度及相对精度与长度变化序列 Fig.4 Sequence diagram of baseline accuracy and length change |
由图 4可见:①4种模型的基线精度均值分别为6.3 mm、6.4 mm、6.4 mm、6.4 mm,变化趋势基本一致,表现为距测站越远,基线解算精度越差;②在长度4 000 km以上,精度开始发生突变(组成4 000 km以上长度的基线两端测站为陆态网络站与IGS站),相对精度达10-9,满足高精度解算要求,且4种海潮模型基线相对精度差别不大。
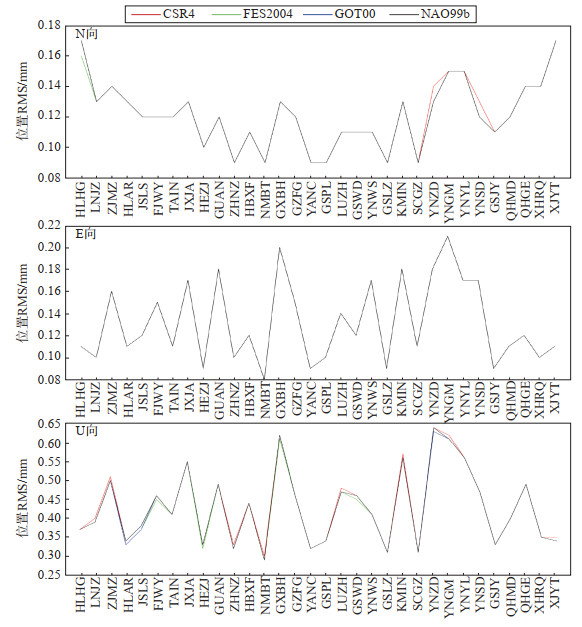
2.2 坐标结果对比联合全球IGS站,利用GLOBK软件对GAMIT软件解算的H文件进行网平差计算,坐标框架选择itrf2008参考框架,得到基于相同框架下不同海潮模型改正的基站三维位置坐标及精度,各测站三方向定位精度均值见见表 3。以云南耿马站(YNGM)坐标为基准,计算并绘制在4种海潮模型下,各测站N、E、U向位置解算精度,见图 5。
| 表 3 N、E、U向各测站精度均值 Table 3 Mean value of accuracy of each station in N, E, U directions |
|
图 5 不同海潮模型影响下站点定位精度 Fig.5 Station positioning accuracy under the influence of different sea tide models |
结合表 3、图 5可知,各测站位置标准差均在1 mm以下,且相差不大,其中FES2004模型解算精度值更小,在通用范围内,可选择该模型进行测站位置解算。
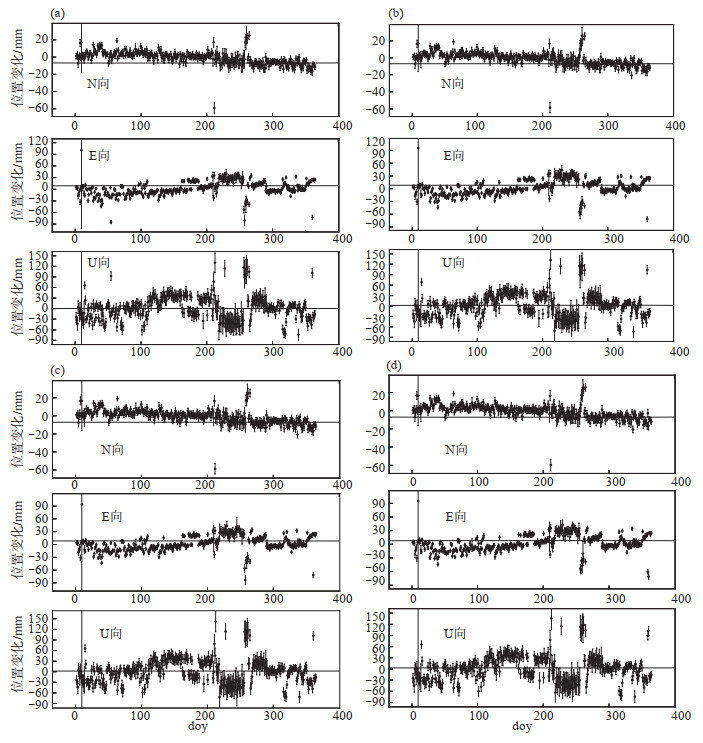
2.3 时间序列对比选用同一参考框架,分析各站点位置时间序列解算结果。文中以云南耿马站(YNGM)位置原始数据(未经滤波)为例,分析该站点时间序列变化,结果见图 6。由图 6可见,在4种模型下,时间序列变化较为一致,在趋势变化背景下,呈不同程度的跳跃,表明受同一因素影响较大,但站点运动趋势较为一致;CSR4模型的E向误差较大,FES2004模型的各向偏差趋势波动较其他模型弱,表明该模型年序列图更连续、稳定。
|
图 6 不同海潮模型影响下云南耿马站(YNGM)时间序列 (a)CSR4模型;(b)FES2004模型;(c)GOT00模型;(d)NAO99b模型 Fig.6 Time series of YNGM under the influence of different ocean tide models |
采用CSR4、FES2004、GOT00、NAO99四种海潮模型,对部分陆态网络站点位置进行实例解算分析,由基线、定位、时间序列结果可知:在所选陆态网络站点范围内,4种海潮模型均满足高精度定位解算要求,定位结果相差不大。利用不同海潮模型解算基线精度,水平方向相差不大于1 mm,垂向相差不大于3 mm,各测站位置标准差均在1 mm以下。简言之,在CSR4模型下,对基线的解算效果较好;在FES2004模型下,对站点位置和时间序列的解算结果均较好。
雷锦韬, 李裴, 张胜凯, 等. 不同海潮模型对东南极沿海地区GPS基线解算的影响[J]. 武汉大学学报(信息科学版), 2015, 40(11): 1479-1486. |
刘洋洋, 党亚民, 许长辉, 等. 海潮负荷对不同地区GNSS基准站的定位影响分析[J]. 测绘科学, 2019, 44(2): 1-5. |
孙和平, 周江存, 许厚泽. 中国地壳运动观测网络基准站应变场变化的海潮负荷信号改正问题[J]. 测绘学报, 2002, 31(3): 222-227. DOI:10.3321/j.issn:1001-1595.2002.03.008 |
张杰, 李斐, 楼益栋, 等. 海潮负荷对GPS精密定位的影响[J]. 武汉大学学报(信息科学版), 2013, 38(12): 1400-1404. |
翟丽娜, 王松阳, 孔祥瑞. 海潮负荷对大连地震台重力固体潮的影响[J]. 地震地磁观测与研究, 2021, 42(2): 214-216. DOI:10.3969/j.issn.1003-3246.2021.02.069 |
赵红, 张勤, 黄观文, 等. 基于不同海潮模型研究海潮负荷对GPS精密定位的影响[J]. 大地测量与地球动力学, 2012, 32(5): 108-112. |
周江存, 孙和平. 海潮负荷对GPS基线的影响[J]. 大地测量学与地球动力学, 2005, 25(4): 27-32. |
Baker T F, Curits D J, Dodson A H. Ocean Tide Loading and GPS[J]. GPS word, 1995, 6(3): 54-59. |
King M A. Validation of ocean tide models around Antarctica using onshore GPS and gravity data[J]. Journal of Geophysical Research: Solid Earth, 2005. |
Vey S, Calais E, Llubes M, et al. GPS Measurements of Ocean Loading and Its Impact on Zenith Tropospheric Delay Estimates: A Case Study in Brittany France[J]. Journal of Geodesy, 2002, 76(8): 419-427. DOI:10.1007/s00190-002-0272-7 |
 2022, Vol. 43
2022, Vol. 43

