0 引言

地磁观测用于地震预测研究已有多年，且取得了较好的进展。但地磁相对观测中哪个分量与地震孕育发生间关系较密切还不太明确。鉴于此，我们利用希尔伯特-黄变换方法（以下简称HHT方法）（Huang et al，1998, 2003）的频谱方法对地磁相对观测数据进行处理和分析。

HHT方法是Hilbert Huang等提出的一种新的信号处理方法。该方法首先对信号进行经验模态分解（empirical mode decomposition，简称EMD）（罗奇峰等，2003），有效地把各种频率成分以本征模态函数（intrinsic mode function，简称IMF）的形式从原始信号中分离出来，然后对上述分离出来的IMF利用Hilbert变换进行计算，并对计算结果在整个时间区间内进行积分，最终得到希尔伯特边际谱（公茂盛等，2003）。类似于通常频谱分析方法，利用该方法也可以得到研究信号的优势频率。安张辉等（2011）利用该方法对地电场观测数据中受城市轨道交通的干扰进行了数据剥离和分析，将数据受城市铁路干扰的程度降到了最低。

1 HHT方法计算原理

利用Hilbert-Huang（HHT）方法分析数据，即通过经验模态分解，将信号分解成一系列本征模态函数，再通过Hilbert变换得到三维时频空间的Hilbert谱（罗奇峰等，2003；石春香等，2003；段生全等，2005；葸晓宇等, 2006, 2007；张立等，2007；周挚等, 2008, 安张辉等，2010）。

对于任意1个时间序列X(t)，其Hilbert变换定义为

$ Y(t) = \frac{1}{\pi }\int {\frac{{X(\tau)}}{{t - \tau }}} {\rm{d}}\tau $

(1)

通过式（1）变换，X(t)、Y(t)可以组合成1个复数信号Z(t)

$ Z(t) = X(t) + iY(t) = a(t){{\rm{e}}^{i\theta (t)}} $

(2)

其中，$a(t) = \sqrt {{X^2}(t) + {Y^2}(t)}, \theta (t) = \arctan \left[ {\frac{{Y(t)}}{{X(t)}}} \right]$。HHT变换可以简单地看成信号序列与$\frac{1}{t}$的卷积，因此，对信号的局部特性进行了突出体现。此时，可以定义瞬时频率为

$ \omega (t) = \frac{{{\rm{d}}\theta (t)}}{{{\rm{d}}t}} $

(3)

为了使瞬时频率具有意义，进行Hilbert变换的信号序列必须是单组分的，即时间与频率间必须是一一对应的关系。经过经验模态分解所得到的本征模态函数可满足该要求，对X(t)的n阶本征模态函数分别进行Hilbert变换后，原始时间序列可以表示为

$ H(\omega, t) = {\mathop{\rm Re}\nolimits} \sum\nolimits_{j - 1}^n {{a_j}(t){{\rm{e}}^{\left. {i[i]{\omega _j}(t){\rm d}t} \right]}}} $

(4)

将式（4）称为X(t)的Hilbert谱，记为H (ω, t)。式（4）中省略了残余项Rn(t)。a_j(t)和ω_j(t)均为时间的函数，把振幅显示在频率时间平面上便可得到Hilbert谱H(ω, t)。如果对H(ω, t)进行时间积分，则可以得到Hilbert边际谱

$ H(\omega) = \int_{ - \infty }^{ + \infty } H (\omega, t){\rm{d}}t $

(5)

边际谱通常代表某固定频率在整个时间区域上所有振幅的总和。

2 震例分析 2.1 汶川M_S 8.0地震

成都地磁台始建于1971年，1997年地磁相对观测仪器正式观测 ，2000 年该台进行了数字化改造，M15观测仪器于2007年开始运行，观测数据准确可靠，台站周边环境良好，干扰较少。成都地磁台距汶川地震震中约100 km。

重庆地磁台始建于1982年2月，1992年成为国家Ⅱ类地磁台。2000年增上DI仪观测；2007年6月、7月先后安装2套GM4磁通门磁力仪，完成数字化改造。后因台站环境遭到破坏，2011年重庆地磁台停测。重庆地磁台距汶川地震震中约100 km。

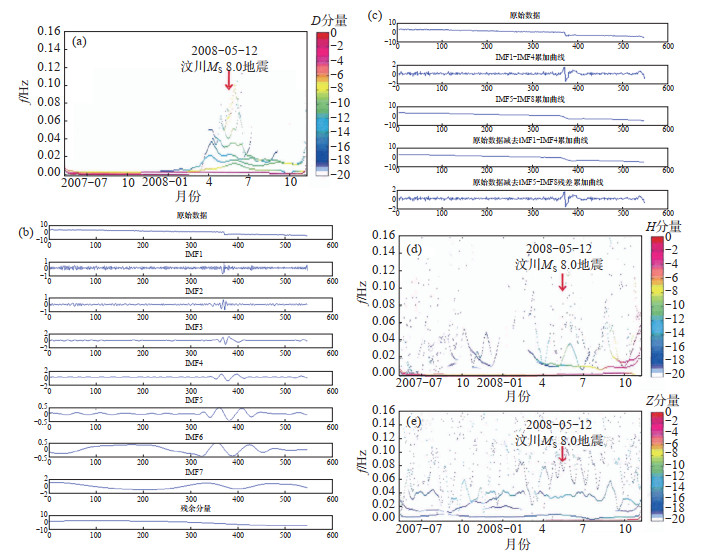
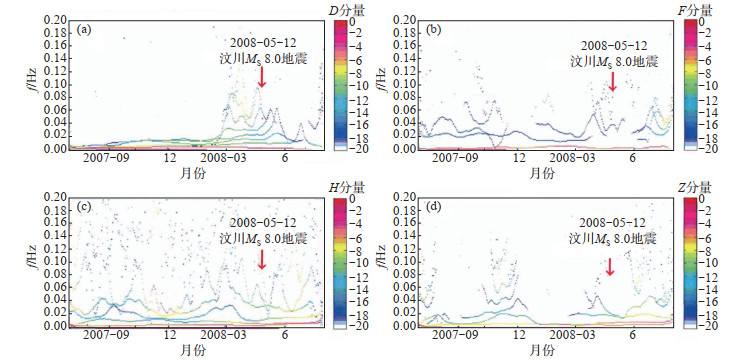
由前述可见，利用HHT数据处理方法进行分析，不受数据采集频率和振幅的影响，可随意定制处理，一般干扰在IMF1—IMF4就已经分解完毕。因此，在数据干扰无法判别时，可以用IMF5—IMF8的数据正常分析（限于篇幅，后面图件略），且不受其他因素的影响。图 1、2分别为成都地磁台2007年7月至2008年10月和重庆地磁台2007年9月至2008年6月地磁观测HHT频谱。由图 1、2可见，频率基本稳定不变，发生频率扰动的时刻反映了HHT所具有的瞬时特性，频谱图中较好地显示出分量优势频率为0.01 Hz，且各测向优势频率基本一致。由图 1、2还可见汶川M_S 8.0地震前兆异常的同震变化情况，成都地磁台、重庆地磁台地磁相对观测分量不同，HHT谱能量积累过程也不同，磁偏角D分量震前能量积累过程较集中、明显。

2.2 汶川M_S 8.0地震余震

拉萨地磁台位于拉萨市西郊“七一”农场内，其海拔高度约3655 m，是中国地震局地磁基本台网Ⅰ类基准台。台站建设于1957年4月完工，台基为砾石冲积层，厚约70 m，周围无明显干扰源，观测区磁场梯度为1 nT/m，分布较均匀。地磁绝对观测室（2006年“十五”数字地震观测网络项目新建）和相对记录室（2008年“子午”工程新建）为无磁或弱磁性材料的地面建筑。

2007年10月23日拉萨地磁台安装了地磁GM4数字磁通门磁力仪和FHDZ-M15地磁组合观测系统，实现了数字化观测，同时撤掉了57型记录仪、CB3型记录仪、Schmidt偏角磁力仪。台站使用M15组合观测系统、GM4磁通门磁力仪2套仪器对地磁场D、H、Z、F分量进行数字连续记录，其中，CTM-DI地磁经纬仪观测地磁D、I分量，G856仪、FHDZ-M15地磁观测系统对F分量进行绝对观测。

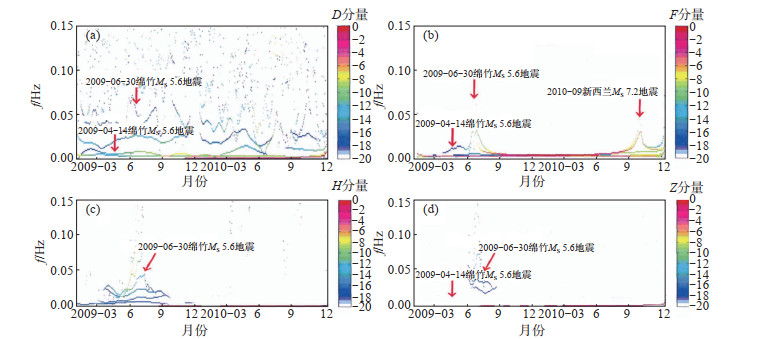
图 3是拉萨地磁台2009年3月至2010年12月地磁观测HHT频谱图。由图 3可见，频率基本稳定不变，发生频率扰动的时刻反映了HHT所具有的瞬时特性，大部分地磁分量的优势频率为0.01 Hz；地震前地磁总场F分量能量积累过程较显著，其他分量则较弱，能量变化较分散。

3 讨论与结论

如何消除实际信号中的噪声，从混有噪声的信号中提取与地震有关的异常信息一直是地震学研究的热点之一。传统的数据处理方法，如傅立叶变换只能处理线性非平稳的信号，小波变换可处理非线性非平稳信号。而HHT与传统的信号或数据处理方法相比，具有能分析非线性非平稳信号、完全自适应性、不受Heisenberg测不准原理制约——适合突变信号、采用求导得到瞬时频率等特点。因此，HHT方法具有更广阔的应用前景。尽管该方法得到了越来越多的关注，但仍存在以下未能很好解决的问题。

（1）边界处理问题。在HHT方法中，边界处理问题是EMD过程的核心问题，在边界常常出现数据端部的“飞冀”，这使得边界一定区域的数据分解后精度很差。

（2）理论的完备性。在处理非平稳信号时，HHT方法表现出了明显的优越性，但在基础理论方面，相关研究滞后，且缺少对其应用的研究，这包括对EMD和Hilbert变换的数学解释和数学证明。

通过对不同台站、地磁不同观测分量震例HHT频谱进行分析可见，震前有一定前兆反应，尤其是4级以上的中强度地震，大部分地震异常均发生在震前3个月内，且各分量的优势频率均为0.01 Hz。但因观测数据有限，并非震中周边300 km内的所有台站HHT频谱分析结果都反映出前兆异常，这可能还与台站所处的构造位置有关，即沿同一断裂带排列的台站才能监测到地震前兆现象。该问题有待进一步研究。