1 研究背景

图像信息学（Pattern Informatics，缩写为PI）作为一种判定区域中长期地震危险性趋势的统计物理学算法，以小地震活动强的地震区域作为未来可能发生较大地震的危险区，进行预测时段内的定量研究（蒋长胜等，2008；蒋卉等，2013）。

该算法被广泛应用于不同地震活动水平、不同地质构造背景地区的地震活动回溯性研究中，如：美国California地区（Rundle et al，2000；Tiampo et al，2002；Holliday et al，2006）、日本（Nanjo et al，2006）、中国川滇地区（蒋长胜等，2009）、中国山东地区（张盛峰等，2017）和中国青藏高原地区（袁伏全等，2016），均得到了较为有意义的结果。

2 研究内容和方法

PI算法假设地震活动具有“活跃”和“平静”特征的现象，其基本原理是，对研究区域进行网格化处理，通过对每一个网格地震活动强度多时间尺度变化的归一化处理，检测显著事件发生概率高的网格，减去地震背景概率，得到地震热点（Hotspots），即地震危险区。热点值为ΔP_i (t₀, t₁, t₂)，强度函数经归一化处理，用对数lg(ΔP/ΔP_max)值表示，值越大，颜色越深，表示地震危险程度越高。

将研究区进行网格划分，记为X_i，令每一网格X_i地震活动的时间序列为N_i (t)，即第i个网格在单位时间内发生地震的次数，这些地震震级必须大于序列截止震级M_c。定义3个时间范围，见图 1，图中：研究资料起始时刻记为t₀，t_b为以Δt为步长从t₀时刻向t₁时刻滑动的任意时刻，t₁—t₂为地震活动“异常学习”的变化时段，t₂—t₃为地震“预测时段”。Tiampo等（2002）研究发现，PI方法的地震预测效果比相对强度法和随机预测更优越，预测时间尺度为3—10年。

研究用的资料为中国地震台网中心“全国地震编目系统”提供的《统一正式目录》和青海省地震台网地震目录，采用10年尺度的地震“变化学习”时间段和3年尺度“预测”时间段进行统计，对2021年5月22日青海玛多M_S 7.4地震和3月19日西藏比如M_S 6.1地震的预测效果进行回溯性震例分析和“向前”预测。其中，“异常学习”时间段为10年（2008—2018年），“预测”时间段为3年（2019—2021年）。

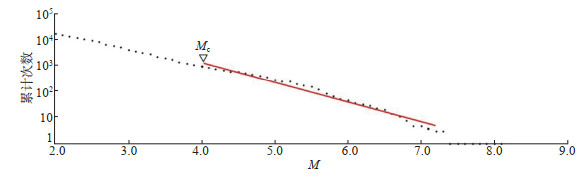
3 研究结果 3.1 截止震级选取

研究区域为（87°—105°E，31°—37°N），所用地震目录时间段为1970年至2021年6月，根据G-R统计关系（图 2），将截止震级（Mc）设定为M_S 4.0，目标震级（M_F）设定为M_S≥6.0。根据不同计算经验，截止震级至少小于预测目标震级2个震级单位（Rundle et al，2000；Holliday et al，2006；Nanjo et al，2006）。

3.2 回溯性检验结果

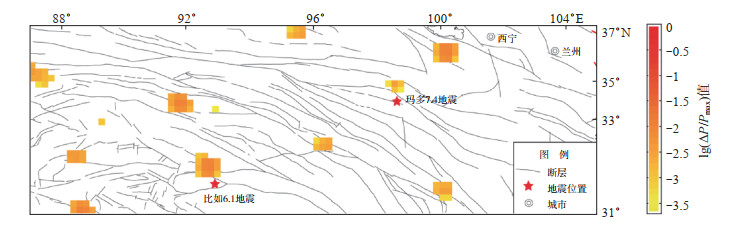
回溯性检验结果表明（图 3），3年预测时间段（2019—2021年）内，截至2021年6月29日，研究区发生2次M_S 6.0以上地震，即青海玛多M_S 7.4、西藏比如M_S 6.1地震，2次地震均位于PI图像的地震热点附近，表明“PI图像热点”具有较好的地点预测能力。

2019—2021年，研究区实际发生M_S 5.0—5.9地震4次，其中2021年3月30日双湖M_S 5.8地震位于PI图像的地震热点附近，其余3次地震漏报，分别为：2020年1月25日丁青M_S 5.1、2020年4月1日石渠M_S 5.6、2019年10月28日夏河M_S 5.7地震。漏报原因可能是多方面的，5级地震不是目标地震，另外算法本身的优化和区域地质背景的不同。在青藏高原地区应用该方法，PI算法包含的各项因子的最佳组合模式，是需要进一步研究的工作。

4 结束语

对2021年5月22日青海玛多M_S 7.4和3月19日西藏比如M_S 6.1地震进行震例回溯性检验，对于地震前可能的地震活动“前兆性”异常进行再认识，对于青海地区地震的中长期预测有一定实践意义。