1 研究背景

目前，在定点形变观测系统中，同一个测点包含多个测项和分量观测，这些观测蕴含不同维度的信息，彼此相互关联，共同反映了孕震区地壳变形信息。因此，需要一种数据降维方法，用于单个测点的信息综合（周硕愚等，1990；牛安福，1999）。另外，震前异常识别及其时空演化的研究，其实质是兼顾物理含义的时空数据挖掘，这种由点到面的空间演化特征研究，亟需构建无量纲参数，以实现单点数据的空间可比。

2 理论基础及研究内容

AF异常综合检测方法是在Fisher检验和动态场分析系统研究基础上完善形成的（Gitis et al，1995），可以较为广泛地对单点或局部多种变形观测进行综合异常检测，具有与变形“势”相同的意义，包括各个方向变形的综合信息。

任一自然过程时常与平稳和非平稳、线性和非线性、异常和正常、确定和随机等特征相联系。为便于描述，可将变形动态过程X_t分解为确定性D_t和随机性S_t两部分。D_t又可分解为平稳的A_t、线性项V_t和低阶非线性项NL_t，S_t可分为平稳的B_t、高阶非线性项H_t和高频随机振荡项R_t，确定性部分D_t通常被接受为正常动态，异常则包含在随机信号中。选取某一“标准时段”对X_t做差分，可将D_t化为线性平稳，而S_t中的高阶非线性项和高频随机振荡R_t仍保留原有特征，从而实现动态变化过程的“捕捉”。

结合观测量物理含义明确、数据质量及连续性相对较好、观测点位分布相对均匀、参考框架统一的GNSS数据，引入AF检验方法，探索GNSS单点时间序列异常及其时空演化特征与地震的关系。GNSS单点时间序列包括线性趋势项、年周期及半年周期项、同震影响（同震阶跃及震后非线性衰减）等，本研究采用Nikolaidis模型，对原始时间序列的线性趋势和同震影响进行拟合并扣除，得到变化相对平稳的数据集。对每一个GNSS点位时间序列N、E、U三分量，分别选取基准时段N₁—N₂，n₁ = N₂ - N₁ + 1，该时段内均值为向量X₀和协方差阵C₀，现时段L₁—L₂，n₁ = L₂ - L₁ + 1，均值向量X₁和协方差阵C₁，进而构造协方差矩阵C = (C₀ + C₁)/(n₁ + n₂ - 2)。定义并标准化Makhahnobis距离，得到统计量F值。F服从Fisher分布F(d，n₂ + n₁ - d - 1)（Gitis，1995），公式如下

$ F = \left({{n_2} - {n_1} - d - 1} \right) \cdot {n_1} \cdot {n_2} \cdot \frac{{{D^2}}}{d} \cdot \left({{n_1} + {n_2} - 2} \right) \cdot \left({{n_1} + {n_2}} \right) $

(1)

若给定信度p = 95%，可得到置信阈值F_p，若F ＞F_p接受为非稳态异常，反之为正常。定义

$ {\rm{AF}} = F/{F_p}(d) $

(2)

设定基准时段数据长度为365天（避免年变影响），待检测时段数据长度为30天，滑动步长30天，计算264个（含境外点）单点时间序列三分量的AF值（月值采样），得到每一个台站的AF异常强度时间序列。

3 研究结果

选取数据连续性较好、无显著干扰的GNSS连续站点，利用Matlab自带的4点样条函数插值算法，得到AF异常时空演化特征图像，以2016年11月25日新疆阿克陶M_S 6.7地震和2017年11月18日西藏米林M_S 6.9地震为例，总结震前异常时空演化特征。

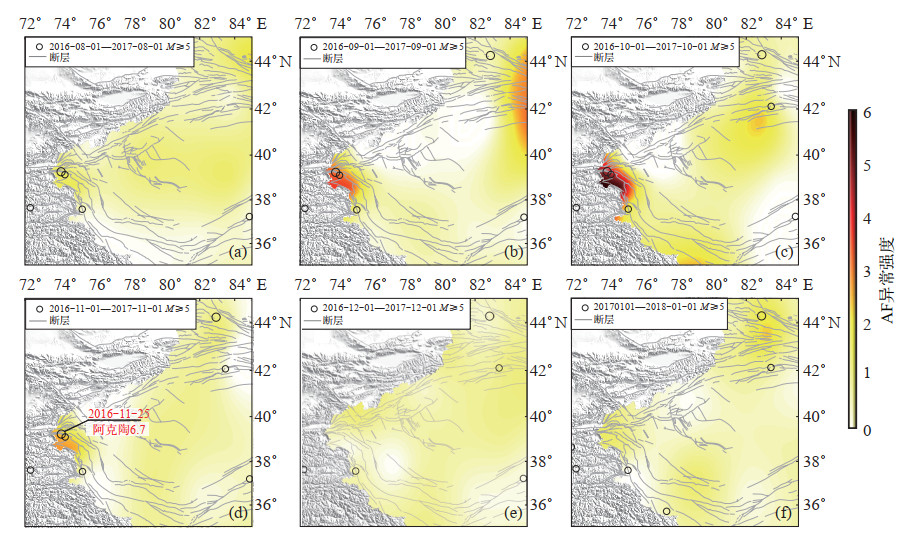
（1）2016年11月25日新疆阿克陶M_S 6.7地震。2016年8月（震前4个月），南天山西段开始出现AF高值异常，后逐渐增强，并于10月达最高值（震前1个月），在衰减过程中发生阿克陶M_S 6.7地震，震后异常消失，震前异常形态表现为增强—减弱—发震的变化过程（图 1）。

（2）2017年11月18日西藏米林M_S 6.9地震。2017年6月（震前5个月），藏东南地区开始出现AF高值异常，后逐渐增强，于同年8月达最高值（震前3个月），同时异常范围逐渐扩大，主体区向北侧移动，后在该区域发生2017年11月18日西藏米林M_S 6.9、2018年5月6日青海称多M_S 5.3和2018年8月3日玉树M_S 5.1地震，异常持续时间分别为5个月、11个月和14个月（图 2）。

4 结束语

通过上述研究，实现了单个GNSS测站AF异常强度计算，以及全国多个台站AF异常强度时空演化特征的总结。震例回溯结果显示，该指标在中国大陆西部地区具有较好的预测意义，震前AF异常多表现为高值—高值增强—高值减弱—发震的演化过程，时间指示意义多为半年至1年尺度。