0 引言

伊舒断裂带是郯城—庐江断裂带北延段进入黑龙江省以后的一个分支，大体NNE走向，从松辽盆地与三江盆地之间穿过，并沿着走向一直延展到俄罗斯境内。大多研究者认为，该断裂是由太平洋板块俯冲变化所形成的，在中生代时期其主要构造运动方式为以EW向拉张形成近SN向裂陷，其间也存在着太平洋板块俯冲引起的断裂带两侧持续挤压作用（陈洪洲等，2001）；在新生代时期，断裂带则以走滑拉分运动方式为主（许浚远，1997）。本文研究区域是伊舒断裂带北段，即依兰—萝北一段（朱玉瑛等，1991）。历史上，该区域多次发生较大震级地震，其中，1963年6月21日萝北发生5.8级地震；1964年3月29日在萝北再次发生4.3级地震；自1975年黑龙江省地震台网建成起，该区域发生4级以下地震200多次，1990年靠近萝北的俄罗斯境内又发生5.1级地震。因此，该区域已被划入黑龙江省地震跟踪监测重点区域之一（吴宝峰等, 2012, 2015）。

利用伊舒断裂带北段4个固定地震台站记录到的远震事件波形，采用频率域反褶积方法提取P波接收函数，采用H—κ叠加方法获得研究区域的莫霍面结构特点及壳内物质泊松比分布，以期为进一步确定壳内物质，探讨该区域孕震机理、动力学模式提供可靠的地球物理学参考。

1 研究方法 1.1 接收函数提取方法

三分量地震计记录到的远震事件时间序列，在不考虑背景噪声的情况下，主要由震源时间函数、射线传播路径、地震计本身的仪器响应等决定（Phinney，1964），所以，远震P波在时间域中地表位移卷积表达式为

$ \begin{aligned} &D_{\mathrm{V}}(t)=I(t) * S(t) \times E_{\mathrm{V}}(t) \\ &D_{\mathrm{R}}(t)=I(t) * S(t) \times E_{\mathrm{R}}(t) \\ &D_{\mathrm{T}}(t)=I(t) * S(t) \times E_{\mathrm{T}}(t) \end{aligned} $

(1)

其中，D_V(t)、D_R(t)、D_T(t)分别为垂直、径向和切向3个分量的波形记录；t为时间；I(t)为仪器响应；S(t)为震源时t间函数；E(t)为台站下方介质结构响应。再利用“等效震源假设”假定（Langston，1979），台站下方介质对远震P波垂直分量在时间域记录中没有影响，介质响应可简单地看作1个狄拉克函数

$E_{\mathrm{V}}(t) \approx \delta(t), \quad E_{\mathrm{V}}(\omega) \approx 1 $

(2)

将式（2）代入式（1）中的远震P波垂直向分量记录卷积表达式中，可得

$ D_{\mathrm{V}}(t) \cong I(t) * S(t) $

(3)

即D_V(t)可理解为因近似远震平面P波垂直入射，所以P波垂直向分量记录不受介质响应的影响，将式（3）代入式（1）中的径向、切向分量记录表达式中得到

$ \begin{aligned} &D_{\mathrm{R}}(t)=I(t) * S(t) * E_{\mathrm{R}}(t) \approx D_{\mathrm{V}}(t) * E_{\mathrm{R}}(t) \\ &D_{\mathrm{T}}(t)=I(t) * S(t) * E_{\mathrm{T}}(t) \approx D_{\mathrm{V}}(t) * E_{\mathrm{T}}(t) \end{aligned} $

(4)

将式（4）进行傅里叶变换，将时间域上的远震P波径向、切向分量记录转换到频率域，再应用卷积定理可得到

$ \begin{aligned} &E_{\mathrm{R}}(\omega)=\frac{D_{\mathrm{R}}(\omega)}{I(\omega) S(\omega)} \approx \frac{D_{\mathrm{R}}(\omega)}{D_{\mathrm{V}}(\omega)} \\ &E_{\mathrm{T}}(\omega)=\frac{D_{\mathrm{T}}(\omega)}{I(\omega) S(\omega)} \approx \frac{D_{\mathrm{T}}(\omega)}{D_{\mathrm{V}}(\omega)} \end{aligned} $

(5)

再将式（5）进行傅里叶逆变换，变换到时间域上，最终得到介质结构响应在时间域上的远震P波径向、切向接收函数。

1.2 莫霍面深度、泊松比的计算

当地震波穿过莫霍界面进行传播时，由于两侧介质波速不同，P波部分能量会转换成S波进行传播，甚至会出现自由表面与莫霍面之间多次转换和反射。利用上述震相与直达P波的到时差计算莫霍面深度的公式为

$ \begin{aligned} &t_{\mathrm{Ps}}=H\left[\sqrt{\left(v_{\mathrm{P}} / v_{\mathrm{S}}\right)^{2}-p^{2}}-\sqrt{1-p^{2} v_{\mathrm{P}}^{2}}\right] / v_{\mathrm{P}} \\ &t_{\mathrm{PpPs}}=H\left[\sqrt{\left(v_{\mathrm{P}} / v_{\mathrm{S}}\right)^{2}-p^{2}}+\sqrt{1-p^{2} v_{\mathrm{P}}^{2}}\right] / v_{\mathrm{P}} \\ &t_{\mathrm{PpSs}+\mathrm{PsSs}}=2 H \sqrt{\left(v_{\mathrm{P}} / v_{\mathrm{S}}\right)^{2}-p^{2} v_{\mathrm{P}}^{2}} \end{aligned} $

(6)

其中，t_Ps、t_PpPs、t_PpSs+PsPs分别为这些震相相对于直达P波的到时差；H为莫霍面深度；v_P、v_S分别为P、S波在地壳中平均速度；p为射线参数。当给定射线参数值时，到时差也可以从接收函数上得到，因此，式（6）可以理解为莫霍面深度与纵波、横波波速比（κ = v_P/v_S）之间的关系式。

实际上，直接从接收函数上获取转换波与多次反射波到时是非常困难的。采用H—κ叠加方法（Zhu et al，2000）来求得莫霍面深度和地壳内波速比。给出地壳内纵波平均速度，再给定莫霍面深度H和波速比κ取值范围，将扫描到的H和κ值代入式（6）算出各个震相相对于直达P波的到时差，同时可得到在接收函数上各个震相对应振幅的大小，再将每个震相振幅按照以下目标函数进行叠加

$ s(H, \kappa)=w_{1} r\left(t_{\mathrm{Ps}}\right)+w_{2} r\left(t_{\mathrm{PpPs}}\right)+w_{3} r\left(t_{\mathrm{PpSs}}+\mathrm{PsPs}\right) $

(7)

其中，r(t)为径向接收函数；ω₁、ω₂、ω₃为震相振幅叠加权重系数，并且满足绝对值相加等于1。式（7）取得最大值，也就是震相叠加后的能量最大值，说明每一个震相的到时与实际到时是对应的，此时得到的地壳厚度H和波速比κ也接近真实值的最佳结果（张宝文等，2015）。最后，根据波速比推算出泊松比，其关系式为

$ \sigma=\frac{1-\frac{1}{2} \kappa^{2}}{1-\kappa^{2}} $

(8)

2 观测资料的选取与处理

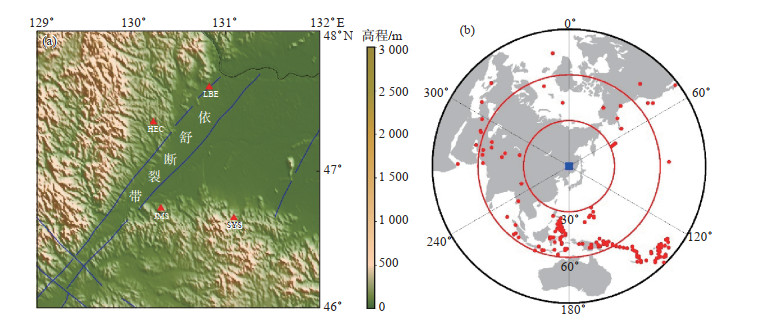
选取位于伊舒断裂带北段的萝北地震台（LBE）、鹤岗地震台（HEG）、佳木斯地震台（JMS）、双鸭山地震台（SYS）记录到的，2017年1月至2018年9月面波震级大于5.5，震中距为30°—90°的远震地震事件。从中挑选P波初动清晰、信噪比较高的事件，最终挑选得到261个地震事件（图 1）。由图 1可见，所选地震事件的震中位置相对研究区域台站的反方位角有较好的覆盖。利用SAC软件截取各个台站地震记录P波到时前10 s到后80 s共90 s的波形数据，同时完成去仪器响应、去趋势、去均值、坐标系旋转、滤波等数据预处理工作；然后，运用频率域反卷积的方法提取所有远震事件的P波径向接收函数。计算过程中，选择不同参数进行测试后，高斯滤波系数选取1.0，水准量选取0.01（吕睿等，2016）。

在利用H—κ叠加方法计算莫霍面深度和波速比时，结合杨宝俊（1999）的人工地震剖面测深结果进行分析，得出给定地壳内P波平均速度为6.3 km/s时最合理；莫霍面深度H和波速比κ搜素范围分别设定为20—60 km和1.5—2.0，且H和κ的搜索步长分别为0.1 km和0.01。根据实际接收函数波形，最优振幅加权系数分别给定为0.7、0.2、0.1。

3 结果与讨论

经过前文所述的数据处理流程后，得到伊舒断裂带北段区域内4个固定地震台站下方莫霍面深度及泊松比，并将其与张广成（2012）研究结果进行对比（表 1）。

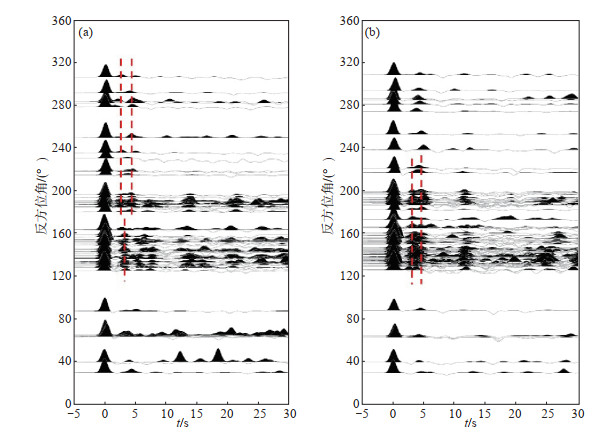
从表 1可见，2种方法所得的莫霍面深度，双鸭山地震台台（SYS）的相差9.0 km，萝北地震台（LBE）的相差1.5 km，均在误差范围内，其他台站的莫霍面深度无太大差别。2种方法所得的波速比，相对其他台的差异，鹤岗地震台（HEG）差异较大，双鸭山地震台差异较小。为了探究其原因，再将2个台的径向接收函数按照反方位角从小到大排列（图 2）。从图 2可见，鹤岗地震台（HEG）反方位角大于180°时，即P波从台站西侧入射时，在约2.8 s处有1个明显波峰，利用反方位角小于180°的接收函数再进行计算，得到莫霍面深度为32 km，波速比为1.642；双鸭山地震台（SYS）在反方位角为120°—280°、大致方向为WN—ES向时，在3.0—4.8 s之间有明显的震相叠加。在双鸭山地震台（SYS）观测到的现象与张广成（2012）的结果相似，符合其提出的双莫霍界面结构的推测。

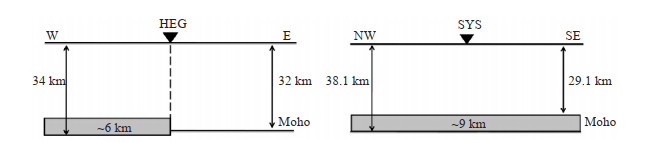
根据上述讨论，推测了鹤岗地震台（HEG）、双鸭山地震台（SYS）下方简单的莫霍界面结构模型（图 3）。鹤岗地震台下方西侧莫霍面深度为34 km，而且上方大约6 km处还存在1个速度间断面，其东侧的莫霍面深度为32 km；而双鸭山地震台WN—ES方向上，莫霍面出现了错断层叠，有了一定的厚度，造成本文计算所得双鸭山地震台莫霍面深度与前人结果不同。

泊松比对岩石组成成分的变化非常敏感，因此泊松比的大小及变化常用来推断地壳（尤其是下地壳）物质成分组成及运动演变过程。一般认为，低泊松比值（σ＜0.26）代表地壳中长英质矿物含量高的物质居多；中间值（0.26≤σ≤0.28）代表地壳物质中长英质与铁镁质矿物的含量相当的中间型；高泊松比值（σ＞0.28）代表铁镁质矿物含量高的物质构造（Holbrook et al，1992）。伊舒断裂带北段区域内4个固定地震台站泊松比为0.266—0.277，属于中间值，说明台站下方地壳物质岩性为长英质与铁镁质含量相当的中间型。因此推测，由于太平洋板块俯冲作用，伊舒断裂带北段长期处于强烈持续挤压状态，造成深切地壳的断裂带两侧岩石破碎，应力得到了释放，上地幔物质上涌到下地壳中，甚至可能在下地壳中以部分熔融状态存在，致使该断裂带附近的台站下方地壳增厚，泊松比增大，这也说明了伊舒断裂带北段是一个地震活动性较强的大规模岩石圈破裂区。

4 结论

选取伊舒断裂带北段4个地震台记录到的震中距为30°—90°、面波震级大于5.5的远震地震事件，提取P波径向接收函数；再采用H—κ叠加方法计算各台站下方的莫霍面深度和泊松比。得到以下结论。

（1）各台站接收函数信噪比较高，关键震相清晰，反演得到的莫霍面深度及泊松比结果精确可靠。

（2）除双鸭山地震台外，其他台站莫霍面较深，大于全球平均的33 km；且双鸭山地震台接收函数波形上有莫霍面错断叠置的结构发生，鹤岗地震台西侧莫霍面上方存在1个明显的速度间断面。

（3）各台站下方泊松比较高，为0.266—0.277；地壳较厚，泊松比值较高，反映了上地幔铁镁物质上涌到下地壳中。

（4）莫霍面结构与泊松比值的特点也验证了在太平洋板块俯冲作用的影响下块体间的挤压致使研究区域存在复杂的构造背景。