震级是对地震大小的量度,是地震的基本参数之一,在地震监测、预测、信息发布、科学普及、新闻报道、防震减灾中具有重要作用(陈运泰等,2004;国家质量技术监督局等,2004),是地震研究中的重要参数之一。震级国家标准GB 17740—1999《地震震级的规定》(国家质量技术监督局,2004)自实施以来,规范了地震震级的测定方法和使用,在地震监测、震害防御、应急救援等防震减灾相关工作中发挥了重要作用,取得了良好的科学效益和社会效益(中华人民共和国国家质量监督检验检疫总局等,2017)。
2001年,基于国家标准GB 17740—1999《地震震级的规定》(国家质量技术监督局,2004),中国地震局颁布了《地震及前兆数字观测技术规范(地震观测)》(以下简称“规范”),规定我国地震台站(网)在日常地震监测中要测定地方性震级ML、水平向面波震级MS、垂直向面波震级MS7、短周期体波震级mb、中长周期体波震级mB等5种震级(中国地震局,2001),这些震级均基于模拟地震记录。
目前,我国地震观测系统实现了数字化和网络化,地震台站全部升级为数字化台站。仪器特性、数据传输方式、数据分析处理方式、震级测定的时效性等都发生了根本变化。自GB 17740—1999《地震震级的规定》(国家质量技术监督局,2004)实施以来,我国已经积累了大量的地震观测资料,在地震震级测定方面有了新的认识(中华人民共和国国家质量监督检验检疫总局等,2017)。随着数字地震观测系统的广泛应用,震级测定方法研究也取得了重要进展,矩震级测定被纳入国际主流地震监测机构日常工作,国际地震学与地球内部物理协会(IASPEI)也制定了新的震级标准,我国与国际主流地震监测机构在震级测定方面的差异逐渐显现(Bormann et al,2008;IASPEI,2013;刘瑞丰等,2015;王丽艳等,2016)。为此,中国地震局于2011年成立项目组,开展震级国家标准的修订工作,新的震级国家标准GB 17740—2017《地震震级的规定》(中华人民共和国国家质量监督检验检疫总局,2017)于2017年5月12日正式发布,新标准对地方性震级ML、面波震级MS、宽频带面波震级MS(BB)、短周期体波震级mb、宽频带体波震级MB(BB)和矩震级MW等6种震级标度的测定方法及使用作出了规定。
新的震级国家标准保留了ML、MS和mb,取消了MS7和mB,增加了IASPEI推荐的MS(BB)、MB(BB)和MW,既在一定程度上保持了震级测定的连续性,同时也充分借鉴了国内外震级测定方面的研究成果,最大程度上实现了与国际主流地震监测机构震级标度的一致。
对于同一次地震,使用不同的震级标度测定,通常会得到多个不同的震级,而不同震级标度测定值之间的关系一直是研究者所关注的重要研究课题(刘瑞丰等, 2005, 2006, 2007;Castellaro et al,2007;任克新,2008;杨晶琼等,2016)。新的震级国家标准在测定方法、测定结果方面与原规范中的震级间具有怎样的关系?值得深入研究。对新的国家标准震级标度与原规范涉及的震级种类较多,震级测量分向一致、震相相同、适用震中距范围和地震波周期相近的震级标度之间的比较,对于确定同类型震级之间的关系更具意义。因此,以陕西地震台网2008年5月至2021年5月记录到的104次ML≥4.5地震为研究对象,使用差值统计和线性回归方法,对新的国家标准震级标度中的ML、MS(BB)与原规范中的ML、中国地震台网的MS以及MW进行对比。
1 地方性震级ML的对比 1.1 计算公式和测量方法的差别新国标ML震级与旧国标ML震级相比,计算公式相同,均为
| $ M_{\mathrm{L}}=\lg A+R(\Delta) $ | (1) |
它们的差别主要体现在2个方面:一是仿真模式。原规范规定,可以仿真成DD-1型或W.A.型短周期记录,新标准规定则只能仿真成DD-1型。二是量规函数。原规范使用了李善邦(1981)根据Richter(1935)原始形式量规函数并结合我国地震仪器特性和华北地区地震波衰减规律修改后的量规函数R。该量规函数为全国统一的量规函数,并没有考虑到我国地壳结构的分区性,新标准则是根据地震波在不同区域的传播规律建立了分区量规函数。
1.2 对比结果选取2008—2020年陕西测震台网记录清晰且距省边界100 km范围内的56个地震事件,分别对这56个测试地震按照新、旧国家标准进行了ML震级测定。按照要求,波形在仿真成DD-1后在位移记录上量取新国标ML震级,波形在仿真成W.A.型短周期记录后量取旧国标ML震级,详细结果见表 1。
| 表 1 利用新、旧国标测量ML震级结果 Table 1 ML Magnitudes measured by new and old national standards |
对表 1的新、旧国标ML震级作了正交回归分析,新、旧国标ML震级关系如图 1所示,相关系数为0.964 2,RMS为0.103 4,并且新ML震级与旧ML震级间存在以下线性关系
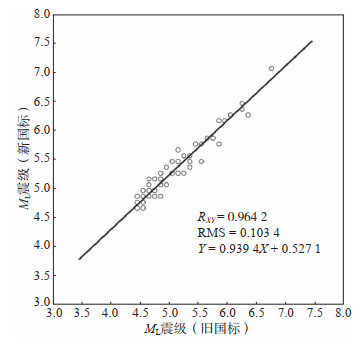
|
图 1 ML震级(旧国标)与ML震级(新国标)间的线性关系 Fig.1 The linear relationship between ML magnitudes measured by old and new national standards |
| $ M_{\mathrm{L}}=0.9394 M_{\mathrm{L}(\mathrm{OLD})}+0.5271 $ | (2) |
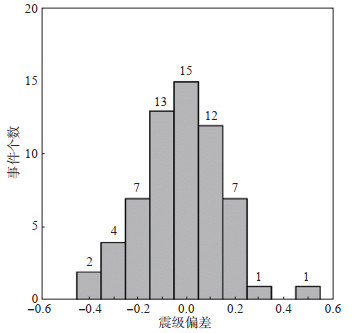
由图 1可见,新、旧国标ML震级之间存在一定的差值,差值分布如图 2所示。由图 2可见,如果以旧ML震级为基准,新ML比旧ML系统性偏大,但总体小于0.3。

|
图 2 新、旧国标ML震级间偏差分布 Fig.2 Distribution of ML magnitude differences measured by old and new national standards |
新国标MS(BB)使用未仿真垂直向记录的最大速度值计算得到,其计算公式为
| $ M_{\mathrm{S}(\mathrm{BB})}=\lg \left(\frac{v_{\max }}{2 \pi}\right)+1.66 \lg \Delta+3.3 $ | (3) |
MS(CENC)使用仿真为基式地震仪后在水平分量量取最大位移计算得到,其计算公式为
| $ M_{\mathrm{S}(\mathrm{CENC})}=\lg \left(\frac{A}{T}\right)_{\max }+1.66 \lg \Delta+3.5 $ | (4) |
而对于MW,可使用波形反演得到,MW能较好地体现地震的量级大小。
为检验MS(BB)震级的稳定性,选取陕西地震台网2008—2020年记录到的M≥4.5地震作为研究对象,并通过国家地震科学数据中心网页和GCMT网页分别查询MS(CENC)和MW震级(Dziewonski et al,1981;Ekström et al,2012;国家地震科学数据中心,2021)。由于有些地震震级偏小,在远台无法观测到长周期面波震相,最终得到62个同时具有MS(CENC)和MW震级记录的地震事件,按照新的标准量取其MS(BB)震级后,对其进行了对比(表 2)。
| 表 2 MS(BB)、MS(CENC)、MW震级对比结果 Table 2 Comparison among MS(BB), MS(CENC), and MW magnitudes |
通过正交回归分析,可以得到MS(BB)震级与MW震级间的关系(图 3),其相关系数为0.952 3,RMS为0.118 5,并且MS(BB)震级与MW震级间存在以下线性关系
| $ M_{\mathrm{W}}=0.9429 M_{\mathrm{S}(\mathrm{BB})}+0.3342 $ | (5) |

|
图 3 MS(BB)震级与MW震级间的线性关系 Fig.3 A linear relationship between MS(BB) and MW magnitudes |
MS(BB)、MW震级的差值分布如图 4所示。由图 4可见,MS(BB)与MW无系统偏差,二者偏差在0附近呈正态分布,大部分偏差为-0.1—0.1。仅个别地震偏差较大,造成这种差异的主要原因可能是使用资料的不同,GCMT在进行矩张量反演时主要使用远台的长周期面波,震中距一般大于1 000 km;而我们量取MS(BB)时主要采用区域台网资料,震中距相对较小,长周期面波可能还未发育完全。
|
图 4 MW震级与MS(BB)震级间偏差分布 Fig.4 Distribution of differences between MW and MS(BB) magnitudes |
通过正交回归分析,可以得到MS(BB)震级与MS(CENC)震级间的关系(图 5),其相关系数为0.964 2,RMS为0.105 9,并且MS(BB)震级与MS(CENC)震级间存在以下线性关系
| $ M_{\mathrm{S}(\mathrm{CENC})}=1.0045 M_{\mathrm{S}(\mathrm{BB})}+0.1929 $ | (6) |

|
图 5 MS(BB)震级与MS(CENC)震级间的线性关系 Fig.5 A lLinear relationship between MS(BB) and MS(CENC) magnitudes |
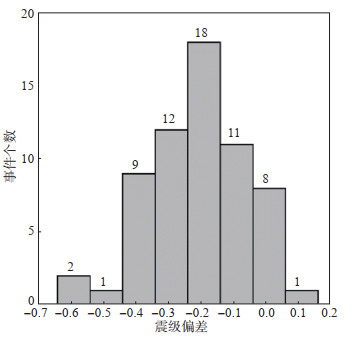
MS(BB)、MS(CENC)震级的偏差分布情况如图 6所示。由图 6可见,MS(BB)比MS(CENC)整体平均偏小0.2,这主要是因为二者的量规函数间存在0.2的差值。
|
图 6 MS(BB)震级与MS(CENC)震级间偏差分布 Fig.6 Distribution of differences between MS(BB) and MS(CENC) magnitudes |
正交回归分析可以看出MS(CENC)震级与MW震级间的关系(图 7),其相关系数为0.945 7,RMS为0.126 6,MS(CENC)震级与MW震级间存在以下线性关系
| $ M_{\mathrm{S}(\mathrm{CENC})}=0.9382 M_{\mathrm{W}}+0.1558 $ | (7) |
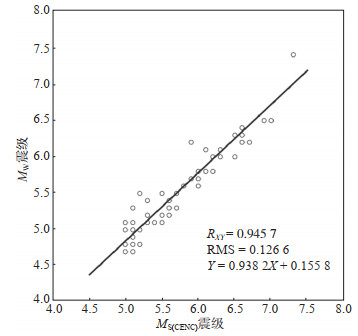
|
图 7 MS(CENC)震级与MW震级间的线性关系 Fig.7 A linear relationship betweenMS(CENC) and MW magnitudes |
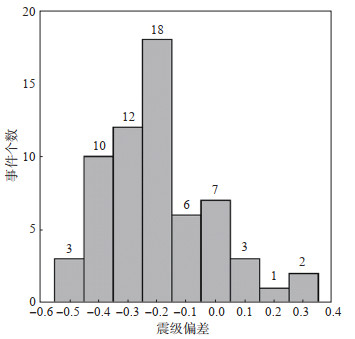
MS(CENC)、MW震级的偏差分布情况如图 8所示。由图 8可见,MS(CENC)震级相比MW震级系统性偏大,绝大多数地震的MS(CENC)比MW偏大0.2—0.3,拟合残差在所述3种震级对比中相对最大。
|
图 8 MS(CENC)震级与MW震级间偏差分布 Fig.8 Distribution of differences betweenMS(CENC) and MW magnitudes |
将新的震级国家标准应用于陕西地震台网得到新国标震级,并与原规范震级进行了分析对比,得到以下结果。
(1)新国标地方性震级ML较旧国标ML震级系统偏大,这主要是采用了新的量规函数。目前,陕西省测震台网使用的是东北、华北地区新量规函数,台站震中距为0—100 km时,新国标中东北、华北地区量规函数比旧国标中量规函数偏大;震中距分别为100—300 km、580—600 km时,新国标中量规函数和旧国标中量规函数基本一致;震中距为300—600 km时,新国标中量规函数比旧国标中的量规函数偏小。总体来看,新量规函数比旧量规函数偏大0.1—0.2。
(2)宽频带面波震级MS(BB)与矩震级MW相比,二者间无系统偏差,绝大多数地震震级差为-0.1—0.1。GCMT公布的MW震级主要由波形长周期面波反演获得,均能较好地描述地震的实际大小。但测定MS(BB)震级时使用的是未仿真的垂直向记录,因此,在震后快速产出效率上,MS(BB)震级更具有优势。
(3)宽频带面波震级MS(BB)比面波震级MS(CENC)整体偏小0.2,二者之间存在系统偏差。
(4)绝大多数地震的面波震级MS(CENC)比MW偏大0.2—0.3,二者之间存在系统偏差。
由此认为,新的国家标准震级标度对传统震级标度有很好的继承和衔接。新国标ML震级较稳定,较旧国标ML震级系统偏大0.3左右。MS(BB)震级具有良好的稳定性,并且只需要在垂直向未仿真状态下量取,震后只需要测量几个较精确的长周期面波震相,即可得到较精确的震级,更便于测量。新的分区量规函数更符合区域地质特性,故可以为震后快速、稳定产出提供有力支撑。
陈运泰, 刘瑞丰. 地震的震级[J]. 地震地磁观测与研究, 2004, 25(6): 1-12. DOI:10.3969/j.issn.1003-3246.2004.06.001 |
国家地震科学数据中心. 中国地震台网(CSN)地震目录[EB/OL]. (2021-06-12)[2021-06-15]. https://data.earthquake.cn/gcywfl/index.html.
|
国家质量技术监督局. GB 17740-1999地震震级的规定[S]. 北京: 中国标准出版社, 2004.
|
李善邦. 中国地震[M]. 北京: 地震出版社, 1981.
|
刘瑞丰, 陈运泰, Bormann P, 等. 中国地震台网与美国地震台网测定震级的对比(Ⅰ)——体波震级[J]. 地震学报, 2005, 27(6): 583-587. DOI:10.3321/j.issn:0253-3782.2005.06.001 |
刘瑞丰, 陈运泰, Bormann P, 等. 中国地震台网与美国地震台网测定震级的对比(Ⅱ)——面波震级[J]. 地震学报, 2006, 28(1): 1-7. DOI:10.3321/j.issn:0253-3782.2006.01.001 |
刘瑞丰, 陈运泰, 任枭, 等. 中国地震台网震级的对比[J]. 地震学报, 2007, 29(5): 467-476. DOI:10.3321/j.issn:0253-3782.2007.05.003 |
刘瑞丰, 陈运泰, 任枭. 震级的测定[M]. 北京: 地震出版社, 2015.
|
任克新, 刘瑞丰, 张立文, 等. IASPEI新震级标度与传统震级标度的对比[J]. 地震地磁观测与研究, 2008, 29(5): 16-21. DOI:10.3969/j.issn.1003-3246.2008.05.003 |
王丽艳, 刘瑞丰, 杨辉. 全国分区地方性震级量规函数的研究[J]. 地震学报, 2016, 38(5): 693-702. |
杨晶琼, 杨周胜, 蔡明军, 等. IASPEI宽频带面波震级与传统面波震级的对比[J]. 地震研究, 2016, 39(2): 303-307. DOI:10.3969/j.issn.1000-0666.2016.02.017 |
中国地震局. 地震及前兆数字观测技术规范: 地震观测(试行)[M]. 北京: 地震出版社, 2001.
|
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB 17740-2017地震震级的规定[S]. 北京: 中国标准出版社, 2017.
|
Bormann P, Joachim. The New IASPEI Standard Broadband Magnitude mB[J]. Seismological Research Letters, 2008, 79(5): 698-705. DOI:10.1785/gssrl.79.5.698 |
Castellaro S, Bormann P. Performance of different regression procedures on the magnitude conversion problem[J]. Bulletin of the Seismological Society of America, 2007, 97(4): 1 167-1 175. DOI:10.1785/0120060102 |
Dziewonski A M, Chou T A, Woodhouse J H. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity[J]. Journal of Geophysical Research: Solid Earth, 1981, 86(B4): 2 825-2 852. DOI:10.1029/JB086iB04p02825 |
Ekström G, Nettles M, Dziewoński A M. The global CMT project 2004-2010:Centroid-moment tensors for 13, 017 earthquakes[J]. Physics of the Earth and Planetary Interiors, 2012(200/201): 1-9. |
IASPEI. Summary of Magnitude Working Group recommendations on standard procedures for determining earthquake magnitudes from digital data[EB/OL]. (2013-03-27). http://www.iaspei.org/commissions/commission-on-seismological-observation-and-interpretation/Summary_WG_recommendations_20130327.pdf.
|
Richter C F. An instrumental earthquake magnitude scale[J]. Bulletin of the Seismological Society of America, 1935, 25(1): 1-32. DOI:10.1785/BSSA0250010001 |
 2021, Vol. 42
2021, Vol. 42

