0 引言

我国开展钻孔应变观测已有60多年的历史，而采用四分量钻孔应变仪进行观测，自仪器结构设计的提出至今已40多年。21世纪初，四分量式钻孔应变仪被纳入中国地震台网，开始全面为我国地震监测、预测、预报服务。据统计，该仪器在我国布设近百台，多次记录到大中地震前后的应变异常（苏恺之，2020），钻孔应变观测的重要实用性正在得到证实和发扬。相关文献有：池顺良等（2014）对四川和青海的四分量钻孔应变仪观测资料进行分析，发现在远距离的汶川、鲁甸、康定地震前，S₁ + S₃和S₂ + S₄两组面应变数据曲线相关系数在震前出现异常；Kong等（2018）、苏恺之等（2018）指出，云南昭通的四分量钻孔应变仪观测资料，在近距离的彝良M_S 5.7和鲁甸M_S 6.5地震前，2组面应变相关系数在震前数天和震时均出现异常变化。

北京时间2015年9月14日18时10分，河北省秦皇岛市昌黎县发生M_S 4.2地震（39.7°N，118.8°E），震源深度14 km，距震中约300 km的易县地震台（以下简称易县台）四分量钻孔应变仪观测数据在震前出现不同程度的异常。文中收集整理易县台四分量钻孔应变仪记录的昌黎M_S 4.2地震数据，计算并提取面应变和切应变异常，分析发现，S₁ + S₃和S₂ + S₄两组面应变相关系数在震前数天出现异常，此为继2014年池顺良等和2018年孔向阳和苏恺之的报道后，再一次出现面应变相关系数异常。

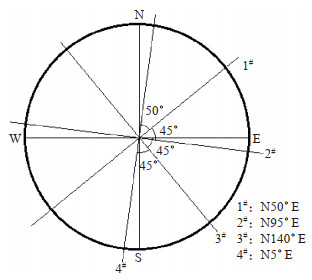
1 台站概况

易县台位于河北省保定市易县西陵镇龙里华村，地处太行山北段丘陵地区，紫荆关断裂带东侧，太行山隆起带与华北平原拗陷区分界部位。该台YRY四分量钻孔应变仪（下文监测钻孔应变仪）于2009年8月安装，孔深38.0 m，井段9—70.3 m为中生代侵入闪长岩。钻孔应变仪有4个受力元件，分别命名为1号、2号、3号、4号，各元件安装位置依次相差45°，但实际角度与理想位置稍有偏差，方位角分别为50°、95°、140°和5°。元件分布示意见图 1。

2 计算原理 2.1 面应变与切应变计算

钻孔内水泥和钢筒各个层位的应力、应变、位移等均有同形式的关系式，只是表达式不同。根据钻孔应变仪安装原理，各元件均匀分布（夹角基本相等），受到岩石应力作用时，应变测值S_i应符合如下关系式（苏恺之，1985；蒲小武等，2013）

$ {S_i} = {A_i}\left({{\varepsilon _1} + {\varepsilon _2}} \right) + B\left({{\varepsilon _1} - {\varepsilon _2}} \right)\cos 2{\theta _i}\;\;\;\;\left({i = 1, 2, 3, 4} \right) $

(1)

式中：S_i为元件测量值依时间的变化量；θ_i为最大主应变方位角；ε₁、ε₂为岩石的最大、最小主应变；A_i为第i号元件对(ε₁ + ε₂)的灵敏系数；B_i为第i号元件对(ε₁ - ε₂)的灵敏系数；(ε₁ + ε₂)为主应变之和，即面应变；(ε₁ - ε₂)为主应变之差，严格来说是最大切应变。

A_i、B_i的值取决于岩石、水泥及钢筒应变仪的力学参数及其边界条件。当A₁ = A₂ = A₃ = A₄ = A，B₁ = B₂ = B₃ = B₄ = B时，有

$ {S_1} + {S_3} = {S_2} + {S_4} = 2A\left({{\varepsilon _1} + {\varepsilon _2}} \right) $

(2)

$ {S_1} - {S_3} = 2B\left({{\varepsilon _1} - {\varepsilon _2}} \right)\cos 2{\theta _1} $

(3)

式（2）表明，1号与3号元件应变测值之和等于2号与4号元件应变测值之和，其变化值仅与面应变(ε₁ + ε₂)有关（苏恺之，2004）。式（3）则表明，1号与3号元件应变测值之差（或者2号与4号应变测值之差）仅与最大切应变(ε₁ - ε₂)有关。

若切应变灵敏系数B已知，则切应变计算公式如下

$ {\varepsilon _1} - {\varepsilon _3} = \frac{{\sqrt {{{\left({{S_1} - {S_3}} \right)}^2} + {{\left({{S_2} - {S_4}} \right)}^2}} }}{{2B}} $

(4)

式（4）的本质是勾股弦定律，(S₁-S₃)和(S₂-S₄)相当于勾和股，最大切应变值则是弦长的1/2（当B = 1时）。

2.2 相关系数计算

设观测数据序列{y_1i}、{y_2i}，i = 1, 2, ..., N，其相关系数定义为k = S₁₂/(S₁S₂)，其中

$ {S_{12}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left({{y_{1i}} - {{\bar y}_1}} \right)\left({{y_{2i}} - {{\bar y}_2}} \right)}, \;S_1^2 = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left({{y_{1i}} - {{\bar y}_1}} \right)}^2}} \\S_2^2 = \frac{1}{N}\sum\limits_{i = 1}^N {{{\left({{y_{2i}} - {{\bar y}_2}} \right)}^2}, {{\bar y}_1} = \frac{1}{N}\sum\limits_{i = 1}^N {{y_{1i}}}, {{\bar y}_2}} = \frac{1}{N}\sum\limits_{i = 1}^N {{y_{2i}}} $

3 震前应变异常分析

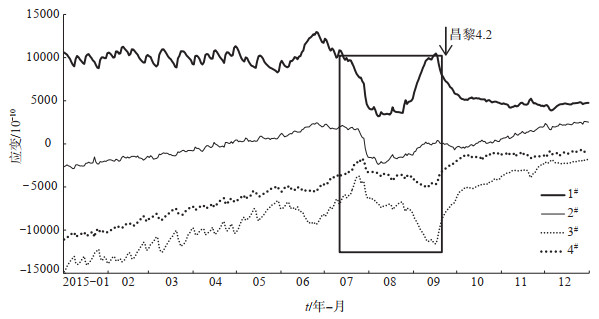
昌黎M_S 4.2地震前，易县台钻孔应变仪四分量在震前均出现大幅度异常变化，且异常形态相似（图 2，图中应变曲线向下为压缩，向上为拉伸）。1号与2号元件应变记录曲线于2015年6月25日出现大幅度下降变化，呈张性状态，8月8日达极值，变化幅度分别为-9 733.161×10^-10，-4 721.042×10^-10，后转为上升恢复阶段。3号与4号元件应变记录曲线于2015年6月25日出现大幅度上升变化，呈压性状态，7月25日和7月28日达极值，变化幅度分别为5 558.441×10^-10和3 633.624×10^-10，后转为下降恢复阶段，并在持续80天后发生昌黎M_S 4.2地震（赵慧琴等，2017）（在A/B具体数值未给定前，设定A = B = 1，对曲线形态无太大影响，仅差一个具体修正值）。

3.1 面应变和切应变异常

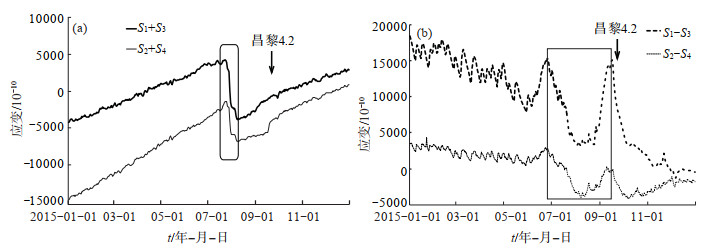
图 3给出易县台钻孔应变观测2015年面应变与切应变曲线。由图 3(a)可见，在异常出现前6个月以上，面应变曲线呈均匀平缓上升趋势，而切应变曲线则近于直线变化，伴有斜率的缓慢变化，表明方位角发生改变。由图 3(b)可见，切应变存在明显的应力波动现象。

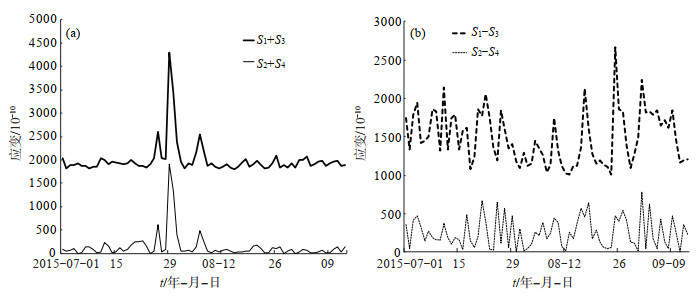
为进一步分析切应变应力波动周期，使用差分绝对值法，对震前约75天的面应变和切应变数据进行一阶差分分析（图 4）。一阶差分是抑制较长周期，突出前兆信息的有效方法，表示曲线变化的速率，可能反映了地壳介质应力变化过程中较高频扰动部分，多属短临前兆。差分值的月或日频次反映了应力扰动的月或日频次。不同台站的构造、介质、电性等条件不同，对应力扰动的响应有所差别，异常判断指标难以统一，可根据某台以往差分值月或日频次对应地震的情况确定相对指标（张凌空等，2013）。

由图 4(a)可见，面应变无明显周期，而切应变应力波动周期约为7天。由图 4(b)可见，在此次昌黎M_S 4.2地震发生前，2组切应变曲线于8月16日—23日在快速下降过程中出现一次近同步的向上抖动，该异常现象是否为震前地壳应力应变的结果，值得深入研究。

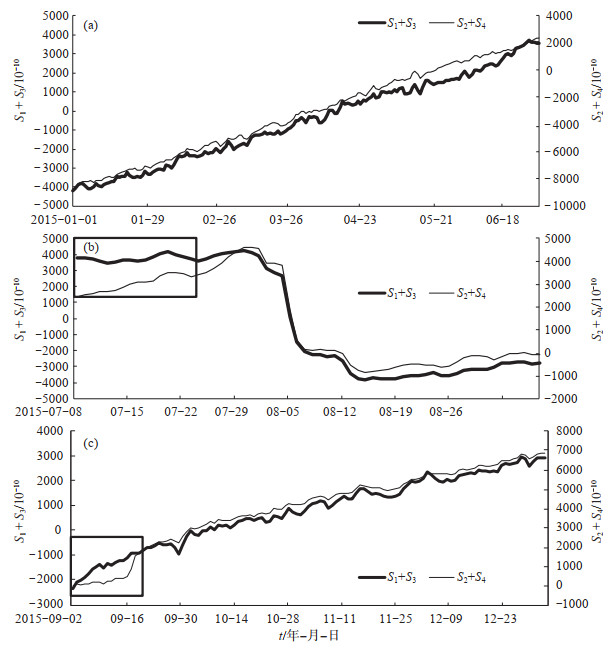
3.2 相关系数异常

选取2015年昌黎M_S 4.2地震发生前后1年面应变观测数据，按1—6月、7—8月和9—12月进行分时段分析，观测曲线见图 5。由图 5可见，1—6月，S₁ + S₃和S₂ + S₄两组面应变曲线近乎同步[图 5(a)]；7月1日—21日[图 5(b)中黑色框线区域]、9月2日—23日[图 5(c)中黑色框线区域]，2个时段内S₁ + S₃和S₂ + S₄两组面应变曲线同步性相对较差，其余时段近乎同步。

根据图 5所示，计算相应时段S₁ + S₃和S₂ + S₄两组面应变的相关系数k，以深入研究面应变曲线变化的同步性。计算结果如下：①2015年1月1日—6月30日：k = 0.996＞0.99；②7—8月：k = 0.975（综合计算）。其中：7月1日—21日，k = 0.676 1＜0.99；7月22日—8月31日，k = 0.998＞0.99；③9—12月：k = 0.988（综合计算）。其中：9月2日—23日，k = 0.843＜0.99；9月24日—12月31日，k = 0.997＞0.99。

由k值计算结果可知，在1—7月、7月22日—8月31日、9月24日—12月31日，k值均大于0.99，表明2组面应变曲线相关性较好，满足自检原理；在7月1日—21日、9月2日—23日，k值均小于0.99，相关性较差，面应变曲线变化不同步。

为寻找异常规律，进一步缩小时间尺度，以天为单位，详细统计震前不同时间S₁ + S₃和S₂ + S₄两组面应变曲线相关系数k值的变化，具体结果见表 1，可见2015年1—7月，2组面应变相关系数k值均大于0.99，8月2日面应变曲线出现差异，k值降低至0.989 1，8月23日面应变曲线出现明显差异，k值继续降低，到9月7日降至0.820 1，7日后发生昌黎M_S 4.2地震。

4 结论和讨论

通过对易县台2015年昌黎M_S 4.2地震钻孔应变观测记录进行分析，可以得出以下结论：①此次地震发生前，钻孔应变仪四分量均出现大幅度异常变化，且形态相似。切应变总变化量不大，但2组曲线出现近同步抖动异常，周期约7天，而面应变出现较大幅度异常，周期不明显；②在此次地震发生前43天起，2组面应变曲线出现分叉现象，相关系数k值由大于0.99下降到0.989 1，之后随着地震的临近，k值继续下降，至震前7天，k值降至0.820 1，并于7天后发震。

与池顺良等（2014）、Kong等（2018）和苏恺之（2018）所分析的震例相比，此次昌黎M_S 4.2地震相对较小，震中距适中，震后2组面应变相关系数在几天至十几天内仍未恢复自洽，与苏恺之（2018）的结论不同，有待进一步积累震例资料进行深入研究。对于震前切应变总变化量不大，而面应变出现较大幅度异常的特异现象，需从地质和断层力学结构等方面进行深入研究。