地球自由振荡是一种重要的地球物理和动力学现象,是指地球局部受到某种因素激发时,地球整体产生的连续振动,如在受到大地震、火山爆发或地下核爆炸激发后,会发生整体振动,并能持续一段时间。地球自由振荡可以变换分解为一些特定的频率,称为地球的本征频率,对应2种本征振荡:①球型地球自由振荡,其质点位移既有径向运动,也有水平运动;②环型地球自由振荡,其质点位移只作水平运动。地球自由振荡的本征频率可以反映地球内部介质的固有特征,准确获得自由振荡的频率特征,可以有效反映地球内部的结构信息。19世纪末期,Lamb从理论上推导出地球自由振荡的存在;1961年,Benionff等使用应变地震仪和摆式仪,准确观测到智利大地震激发的长周期地球自由振荡,确认了地震自由振荡的真实存在(邱泽华等,2007;唐磊等,2007)。21世纪以来,国内外进行地球自由振荡观测主要采用宽频带地震仪、重力仪、应变仪、倾斜仪等灵敏的、可记录长周期振动的高精度仪器。随着各类观测资料的积累,地球自由振荡的理论研究及观测资料的分析已成为探查地球内部结构的有效手段。
20世纪70年代,国际上开始利用倾斜仪观测记录地球自由振荡信号。目前,对于大地震激发的地球自由振荡,国内多针对单台或多台单型号的应变仪、形变仪记录进行球型自由振荡振型的检测分析,取得不少研究成果,如:邱泽华等(2007)利用泰安地震台钻孔差应变仪观测资料、唐磊等(2007)利用中国钻孔应变台网体应变观测资料,杨跃文等(2010)利用云南水管仪观测资料,检测2004年苏门答腊地震激发的地球自由振荡;任佳等(2009)利用垂直摆仪和水管仪观测资料,检测2008年汶川地震激发的地球自由振荡。利用同一场地不同形变测项(倾斜、应变)观测资料进行自由振荡检测,特别是环型自由振荡振型的检测,相关文献较少。
常熟地震台(下文简称常熟台)形变观测山洞进深220 m,环境良好,自2007年起,安装DSQ水管倾斜仪(下文简称水管仪)、VS垂直摆倾斜仪(下文简称垂直摆)、SS-Y洞体应变仪(下文简称洞体应变仪)、TJ-2体应变仪(下文简称体应变仪)等数字化观测仪器,记录的固体潮汐和同震响应清晰,各类测项观测精度均达全国形变Ⅰ类台标准。
利用常熟台水管仪、垂直摆、洞体应变仪、体应变仪观测资料,对2011年3月11日日本9.0级大地震激发的地球基频球型振荡、谐频球型振荡、基频环型振荡进行检测,并与现有PREM模型理论值进行对比分析,研究同一场地各类形变观测仪对地球自由振荡信号的检测能力及共异特性,检定该台站形变观测仪器的运行状态的同时,进一步证明形变仪器对自由振荡的检测效能,检测结果可为约束和改善地球自由振荡模型理论值提供参考。
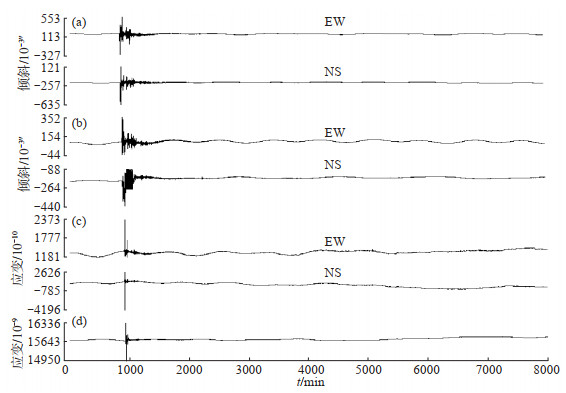
1 观测数据选取及预处理2011年3月11日13时46分在日本本州东海岸附近海域发生9.0级大地震,在造成巨大灾害的同时,为研究地球自由振荡提供了机会,如姚家俊等(2012)、栾威等(2015)、孟方杰等(2018)均对此次地震激发的地球自由振荡进行了相关分析。常熟台水管仪、垂直摆、洞体应变仪、体应变仪清晰记录到此次大地震,其中垂直摆NS向受幅值限制,震时出现暂短靠摆现象,各仪器记录曲线(分钟值)见图 1,图中所用数据均未经干扰消除处理。
|
图 1 常熟形变观测仪对日本大地震的分钟值记录曲线 (a)水管仪EW、NS向;(b)垂直摆EW、NS向;(c)洞体应变仪EW、NS向;(d)体应变仪 Fig.1 Minute value curves of Japan earthquake recorded by Changshu deformation observatory |
据Rosat等(2003)的研究,自由振荡检测的最优起始时间为震后5 h(Rosat,2005)。因此,选取常熟台水管仪、垂直摆、洞体应变仪、体应变仪2011年3月11日17时46分—16日17时46分共5天7 200个分钟值采样数据,提取日本9级大地震激发的地球自由振荡振型。为去除固体潮影响,选用db4小波变换方法对观测数据进行6层滤波预处理(丁浩等,2013),剔除固体潮汐成分,得到数据残差值。
大地震激发的地球自由振荡信号可持续数日至数月,但振荡信号是随着时间衰减的,选取合适的数据长度是能否有效检测更多振荡信号的前提,同时时间长度越长,观测资料携带的背景噪声越多,但某些振型之间的频率间隔太小,若将这些振型清晰分辨出来,要求数据长度(丁浩等,2013)为
| $ T = N\Delta t = 1/\Delta \omega $ | (1) |
式中,N为采样点数,Δt为采样间隔,Δω为最小频率间隔。
综合考虑频谱分辨率与背景噪声水平因素,通过实测比对,选取一定数量的残差数据进行功率谱计算,其中:①洞体应变仪:4 000个残差数据;②水管仪、垂直摆、体应变仪:各5 000个残差数据。
功率谱用于描述随机信号能量特征随频率的变化关系,通常用来描述随机信号的频域特征,也是检测地球自由振荡的主要方法。采用改进的平均周期图法,求取随机信号的功率谱密度估计,并运用信号重叠分段、加窗函数与FFT算法等,提高运算效率与效果。设信号X的自相关函数为Rn,定义其Fourier变换Sk为X的功率谱密度估计(雷湘鄂,2007),即
| $ {S_k} = \sum\limits_{n = 0}^{N - 1} {{R_n}} {{\rm{e}}^{ - i\frac{{2{\rm{ \mathsf{ π} }}nk}}{N}}}\;\;\;\;\;\;k = 0, 1, 2, \cdots, N - 1 $ | (1) |
其中,自相关函数Rn为
| $ {R_n} = \frac{1}{N}\sum\limits_{j = 0}^{N - 1} {{x_j}} {x_{j + 1}}\;\;\;\;\;\;n = - \left({N - 2} \right), - \left({N - 1} \right), \cdots, - 1, 0, 1, \cdots, N - 1, N - 1 $ | (2) |
式(1)、(2)中,N为残差值序列数值长度,x为残差值序列数值,Sk离散值为功率谱密度值。为了消除数据不能无限长而必须加窗对功率谱密度估计造成的影响,采用Hanning窗抑制功率谱旁瓣,突出主瓣。
对于检测频率值是否有效可信,文中参考雷湘鄂等(2007)的甄别方法,利用检测振型的信噪比(每个检测振型的谱峰值与该振型附近观测背景噪声谱的比值,即该振型的信噪比)予以判别,即若被检测振型的信噪比大于3,则检测结果有效,而且检测频率值与理论频率值不能相差太大(胡小刚,2006)。
2 功率谱密度计算结果采用上述方法,计算常熟台4组形变仪观测数据在2011年日本大地震后的功率谱密度估计谱值(PSD),结果见图 2、图 3、图 4,观测频段分别为0.4×10-3—1.8×10-3 Hz、1.8×10-3—3.5×10-3 Hz和3.5×10-3—5.6×10-3 Hz,图中虚线为地球初步参考模型(PREM)的理论频率值,实线表示实测结果。
|
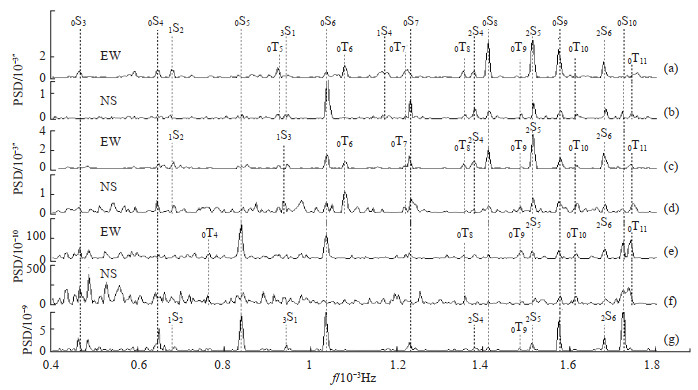
图 2 (0.4—1.8)×10-3 Hz频段形变观测数据功率谱密度估计曲线 (a)水管仪EW向;(b)水管仪NS向;(c)垂直摆EW向;(d)垂直摆NS向;(e)洞体应变仪EW向;(f)洞体应变仪NS向;(g)体应变仪 Fig.2 Power spectral density estimation curves of deformation observation data in (0.4—1.8)×10-3 Hz frequency band |
|
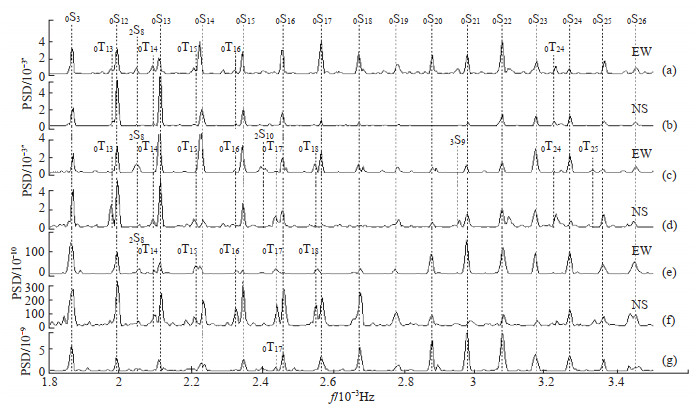
图 3 (1.8—3.5)×10-3 Hz频段形变观测数据功率谱密度估计曲线 (a)水管仪EW向;(b)水管仪NS向;(c)垂直摆EW向;(d)垂直摆NS向;(e)洞体应变仪EW向;(f)洞体应变仪NS向;(g)体应变仪 Fig.3 Power spectral density estimation curves of deformation observation data in (1.8—3.5)×10-3 Hz frequency band |
|
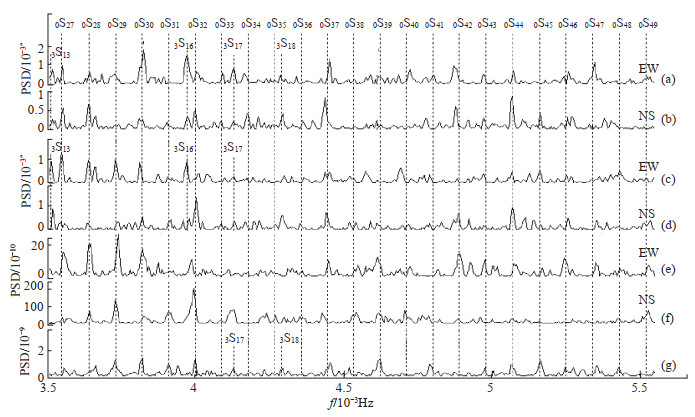
图 4 (3.5—5.6)×10-3 Hz频段形变观测数据功率谱密度估计曲线 (a)水管仪EW向;(b)水管仪NS向;(c)垂直摆EW向;(d)垂直摆NS向;(e)洞体应变仪EW向;(f)洞体应变仪NS向;(g)体应变仪 Fig.4 Power spectral density estimation curves of deformation observation data in (3.5—5.6)×10-3 Hz frequency band |
图 2显示了(0.4—1.8)×10-3 Hz频段内检测的常熟台形变仪观测数据功率谱密度(相对值)与PREM模型给出的自由振荡频率的对应情况。在此频段,常熟台形变观测资料检测到基频球型振型0S3—0S10,基频环型振型0T5—0T11以及谐频球型1S2—1S4、2S4—2S6、3S1。其中水管仪、体应变仪检测到低阶振型0S3、0S4,且振型谱峰较清晰,信噪比>3;垂直摆检测到0S4振型,未检测到0S3振型;洞体应变仪检测到0S3、0S4,振型观测效果不明显,观测值谱峰相对于周边噪声水平未明显分开。
图 3显示了(1.8—3.5)×10-3 Hz频段内检测的常熟台形变仪器观测数据功率谱密度(相对值)与PREM模型给出的自由振荡频率对应情况。在此频段,常熟台形变观测资料检测到基频球型振型0S11—0S26,基频环型振型0T13—0T18、0T24、0T25,谐频球型2S8、2S10、3S9。该频段内无较大干扰,各个振型附近噪声水平较低,观测振型谱峰清晰,与理论值偏离小,信噪比较高。
图 4显示了(3.5—5.6)×10-3 Hz频段内检测到的常熟台形变仪器观测数据功率谱密度(相对值)与PREM模型给出的自由振荡频率的对应情况。该频段内虽然噪声水平较大,但仍较清楚地检测到基频球型振型0S27—0S49以及谐频球型振型3S13、3S16—3S18。在此频段范围内,观测值与理论值的偏离与其他频段比相对较大。
3 计算结果对比分析此次日本9级大地震释放的能量巨大,常熟台形变观测仪不仅检测到0S3—0S49全部基频球型振荡,还检测到基频环型振荡及谐频球型振荡。统计4组形变仪检测的地球自由振荡振型观测频率值和PREM模型理论值的相对偏差,结果见表 1、表 2。
| 表 1 常熟台4组形变仪检测的环型自由振荡值与PREM理论值及其偏差 Table 1 Torsional free oscillation values detected by four groups of deformation instruments at Changshu station and PREM theoretical value and their deviations |
| 表 2 常熟台4组形变仪检测的球型自由振荡值与PREM理论值及其偏差 Table 2 The spheroidal free oscillation values detected by four groups of deformation instruments at Changshu station and the theoretical values of PREM and their deviations |
由表 1、表 2可知:①水管仪检测到45个基频球型振型、10个谐频球型振荡、12个基频环型振型;②垂直摆检测到36个基频球型振型、11个谐频球型振荡、14个基频环型振型;③洞体应变仪检测到41个基频球型振型、3个谐频球型振荡、9个基频环型振型;④体应变仪检测到40个基频球型振型、7个谐频球型振荡、2个基频环型振型。
4组形变仪球型振型观测频率值与PREM理论值整体平均偏差分别为:水管仪为0.112%,垂直摆为0.086%,洞体应变仪为0.088%,体应变仪为0.100%。
常熟台形变仪较清晰检测到与地球内部深部结构有密切关系的低阶基频球型振型0S3、0S4,但观测值与PREM理论值相对偏差高于其他振型,可能存在振型谱线分解现象,能量分散到临近几个频率上(姚家俊等,2012)。除0S3、0S4外,常熟台4组形变仪在低、中频段检测到的基频球型振型谱峰清晰,与PREM理论值相对偏差均低于0.22%(表 1),低、中频段观测振型振幅明显比高频段基频球型振荡振幅高。但随着频率的增加,自由振荡能量逐步衰减,在4.3×10-3 Hz以上频段,部分振型谱峰虽能分辨,但并不突出(图 4),检测的振型观测频率值与PREM理论值相对偏差量明显变大,信噪比较低(表 1),如水管仪0S42振型观测值与PREM理论值偏差为0.339%。观测频率值与理论值偏差较大的原因可能是,高频段的地球自由振荡活动范围随着地球基型振荡阶数的增大趋近于表层,介质的不均匀性和各向异性开始变的明显,即正常观测下的背景噪声影响变高。
与短基线形变仪相比,长基线水管仪、洞体应变仪及深井下体应变仪更容易受到地表高频噪声的干扰。常熟台垂直摆在高频段4.0×10-3—5.6×10-3 Hz噪声水平较高,检测到的自由振荡振型较少,水管仪在0.4×10-3—5.6×10-3 Hz频段背景噪声干扰较小。由表 1、表 2可知,常熟台形变仪检测的基频环型振型、谐频球型振型集中分布在1.0×10-3—4.3×10-3 Hz频段,观测振型谱峰均较清晰,信噪比>3,振型振幅小于基频球型振型;基频环型振型与PREM理论值的相对偏差均低于0.27%,部分基频环型振型与邻近球型振型有不同程度的耦合现象;常熟台形变仪检测的谐频球型振型除1S2、1S3相对偏差较大外,其余谐频球型振型相对偏差小于0.20%。
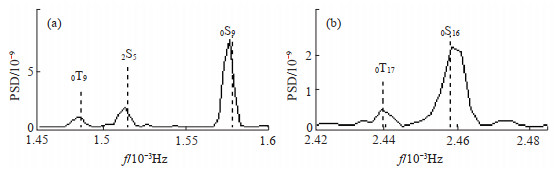
如图 5所示,利用常熟台日本震后5天体应变观测数据,采用小波变换方法,检测到地震激发的2个基频环型振荡:0T9、0T17振型,其观测频率值与PREM理论值相对偏差分别为0.027%、0.041%(表 2),信噪比SNR>3,其他3组形变仪同样检测到2个环型振荡振型。
|
图 5 TJ-2体应变功率谱密度估计 Fig.5 Power spectral density estimation of the observation of TJ-2 volume strainmeter |
检测结果显示:①在倾斜观测仪中,与垂直摆相比,水管仪检测振型数量较多,但整体平均偏差较高。在应变观测仪中,与体应变仪相比,洞体应变仪检测振型总数量较多,整体平均偏差较小;②在4组形变仪中,水管仪检测球型振荡振型(含谐频)能力最强,垂直摆检测环型振荡振型能力最强,从检测自由振荡振型总体数量来看,水管仪潮汐观测精度最高、背景噪声干扰最低,检测的振型数量最多,垂直摆次之,体应变仪最少,表明常熟台倾斜观测仪对自由振荡信号的检测能力优于应变观测仪。
4 结论利用常熟台同一场地观测的4组形变观测仪,检测提取日本9级大地震激发的地球自由振荡信号,不仅准确检测到球型振荡0S3—0S49全部47个基频振型和14个谐频振型,还检测到环型振荡0T5—0T25之间15个基频振型,与PREM理论频率值基本符合,检测结果较好。结果显示,常熟台水管仪检测球型振荡振型能力最强,垂直摆检测环型振荡振型能力最强,且倾斜仪对自由振荡信号的检测能力优于应变仪。
利用小波变换进行潮汐信号滤除处理,对形变观测数据提取地球自由振荡信号效果较好,可有效压制观测数据中的背景噪声干扰,在此基础上,在体应变观测数据中检测到清晰、信噪声比高的基频环型振型。
4组形变观测仪处于同一场地,所检测振型的振幅随着频率的增大出现下降趋势,证明自由振荡信号传播随着频率的增加衰减加快。同时,随着自由振荡阶数的增加,与PREM理论值存在偏差是因为地球介质的横向不均匀或各和向异性,对这些数据加以研究可以得到地球介质的各向异性信息。
地球自由振荡频率可以用来探测地球内部结构,将观测结果与PREM模型理论值进行对比,研究PREM模型与真实地球存在的差异,为约束和改善地球模型提供参考,以使其更接近于真实地球。
丁浩, 申文斌. 探测一阶模态三重分裂的MSE技术和SHS方法的比较研究[J]. 地球物理学报, 2013, 56(10): 3313-3323. DOI:10.6038/cjg20131008 |
胡小刚, 柳林海, 柯小平, 等. 利用小波方法处理2004年苏门答腊大地震后的超导重力数据检测低于1.5 mHz自由振荡信号的耦合和分裂术[J]. 中国科学: 地球科学, 2006, 36(10): 925-935. |
雷湘鄂, 孙和平, 许厚泽. 苏门答腊大地震激发的地球环型自由振荡及其谱线分裂的检测与讨论[J]. 中国科学: 地球科学, 2007, 37(4): 504-511. |
栾威, 申文斌, 贾剑钢. 利用VP型垂直摆倾斜仪观测数据检测2011日本MW 9.0地震激发的低频地球自由振荡[J]. 地球物理学报, 2015, 58(3): 844-856. |
孟方杰, 张燕. 利用不同倾斜仪和应变仪检测地球自由振荡的对比与分析[J]. 中国地震, 2018, 34(1): 133-140. DOI:10.3969/j.issn.1001-4683.2018.01.013 |
邱泽华, 马瑾, 池顺良. 钻孔差应变仪观测的苏门答腊大地震激发的地球环型自由振荡[J]. 地球物理学报, 2007, 50(3): 797-805. DOI:10.3321/j.issn:0001-5733.2007.03.019 |
任佳, 陈华静, 王松, 等. 汶川大地震激发的地球球型自由振荡[J]. 中国地震, 2009, 25(1): 73-80. |
唐磊, 邱泽华, 阚宝祥. 中国钻孔体应变台网观测到的地球球型振荡[J]. 大地测量与地球动力学, 2007, 27(6): 37-44. |
万永革. 数字信号处理的MATLAB实现[M]. 北京: 科学出版社, 2007: 252-279.
|
杨跃文, 秦嘉政, 任佳, 等. 利用云南水管仪观测资料检测地球自由振荡[J]. 地震研究, 2010, 33(2): 189-193. DOI:10.3969/j.issn.1000-0666.2010.02.011 |
姚家骏, 万永革, 王培玲, 等. 利用重力资料检测日本9.0级地震激发的地震自由振荡[J]. 地震研究, 2012, 35(2): 53-58. |
Rosat S, Sato T, Imanishi Y, et al. High-resolution analysis of the gravest seismic normal modes after the 2004 MW = 9.0 Sumatra earthquake using superconducting gravimeter data[J]. Geophys Res Lett, 2005, 32(13): L13304. |
 2021, Vol. 42
2021, Vol. 42


