作为一种全局优化算法, 模拟退火算法因算法简单、可对目标函数全局寻优且不易陷入局部极小值, 最初被应用于计算机辅助设计、图像处理、代码设计等领域, 帮助解决组合优化问题(Van Laarhoven et al, 1987), 继而被广泛用于地球物理反演。1994年Billings将模拟退火算法引入地震定位, 发现可以得到更可靠和准确的全局最小值解。此后, 利用模拟退火算法, Gao等(2002)对1999年9月21日中国台湾集集地震进行了重定位, 窦立婷等(2018)、杨波等(2019)对模拟地震数据和少量大陆震例进行了地震定位, 尹奇峰等(2019)对井中微地震事件进行了反演定位, 均表明模拟退火算法能够对实际地震事件进行地震定位, 具有地球物理实用价值。与Geiger(1912)提出的经典线性方法相比, 模拟退火算法在解决地震定位问题时避免了线性方法处理过程中容易出现的高阶项省略、初始模型选定等问题, 不会出现线性迭代中陷入局部极小值的情况(师学明等, 2007; 田玥等, 2002)。此外, 模拟退火算法不需要进行偏导数计算, 可以使用更少的计算量定位到全局最小值附近, 有效提高了计算效率和精度(Billings, 1994)。
为验证模拟退火算法在江苏及邻区地震事件定位的适用性, 文中利用P波走时数据构建全局寻优模型, 以2019年4月6日江苏溧水ML 3.3地震为例, 进行反演试算, 确定合适的初始温度、扰动函数和降温策略, 运用于2019年江苏省测震台网中心记录的105次ML≥1.8地震事件重定位, 并对定位误差进行分析。
1 算法原理模拟退火算法(Simulated Annealing)是一种解决非线性问题的直接反演方法, 其基本思路是, 假设物质处于状态m0(即模型参数), 该模型对应的能态为E(m0), 利用扰动函数, 在一定范围内对初始模型m0进行扰动, 得到新模型mi, 对应能态为E(mi); 计算2个模型的能量差ΔE, 即ΔE = E(mi) - E(m0), 若ΔE<0, 则接受新模型mi, 若ΔE>0, 则有一定概率接受该新模型, 如果0—1之间的随机数R<P [P = exp (-ΔE/T)(T为绝对温度)], 则接受该新模型, 并以之替代旧模型, 否则重新产生新模型; 当有新模型被接受时, 即以一定策略进行降温, 不断循环直至模型收敛, 迭代结束(师学明等, 2007; Sen et al, 2013)。由于ΔE>0时, 新模型有一定概率被选择, 因此的值尤为重要。若T很大, 则P将接近1, 那么每个新模型(ΔE>0)均有类似概率被接受; 若T很小, 则P趋近于0, 反演结果易陷入局部极小值。因此, T应当与ΔE具有相同数量级。本文使用2种扰动函数, 分别为非常快速模拟退火算法(VFSA)和局部收敛加强型方法。
(1) 扰动函数1。Ingber(1989)提出非常快速模拟退火算法(VFSA), 公式如下
| $ {y_i} = T \times {\mathop{\rm sign}\nolimits} (R - 0.5) \times \left[ {{{\left( {1 + \frac{1}{T}} \right)}^{|2R - 1|}} - 1} \right] $ | (1) |
| $ {{\mathit{m'}}_i} = {\mathit{m}_\mathit{i}} = (\mathit{m}_\mathit{i}^{{\rm{max}}} - \mathit{m}_\mathit{i}^{{\rm{min}}}) \times {\mathit{y}_\mathit{i}} $ | (2) |
式中, T为温度, R为0—1之间的随机数, mi′为新模型, mi为旧模型, mi的取值范围是[mimin, mimax]。
(2) 扰动函数2。Pishro-Nik(2014)提出局部收敛加强型方法, 公式如下
| $ \mathit{u} = \mathit{T} \times {\rm{tan}}[\mathit{pi} \times (\mathit{R} - 0.5)] $ | (3) |
| $ \mathit{m' = u} \times ({\mathit{m}_{{\rm{max}}}} - {\mathit{m}_{{\rm{min}}}}) + \mathit{m} $ | (4) |
式中, T为温度, R为0—1之间的随机数, m′为新模型, m为旧模型, m的取值范围是[mmin, mmax]。
2 反演模型构建地震定位可以简化为利用P波到时来确定震源位置。设某次地震事件中共有m个台站记录到直达波, 任一台站位置为(xk, yk, hk), 实际震源位置为(x0, y0, h0), 则直达P波到达台站的走时可以表示为
| $ {\mathit{t}_\mathit{k}} = \frac{{\sqrt {{{({\mathit{x}_\mathit{k}} - {\mathit{x}_0})}^2} + {{({\mathit{y}_\mathit{k}} - {\mathit{y}_0})}^2} + {{({\mathit{h}_\mathit{k}} - {\mathit{h}_0})}^2}} }}{{{\mathit{v}_{\rm{P}}}}}\;\;\;\;\;\;\;\;\mathit{k} = 1,2,3, \ldots ,\mathit{m} $ | (5) |
式中, vP为P波速度。
利用式(5)进行实际反演, 需将经纬度坐标转化到平面坐标系下, 反演结束后再转化为经纬度坐标系。选用江苏省测震台网中心地震定位所用的速度结构, 设定vP = 6.01 km/s。定义模拟退火算法中的能态为, 所有台站记录的直达P波走时tk与P波拾取震相走时ttrue之差的二范数, 即E=‖tk-ttrue‖2, k=1, 2, 3, …, m。
3 震例试算及参数分析以江苏省测震台网中心记录的2019年4月6日江苏溧水ML 3.3地震为例, 进行反演试算, 确定模拟退火算法中的关键参数。在反演过程中, 使用20个地震台站记录的P波到时信息。为确定模拟退火算法中的相关参数, 设定初始温度T为1、25、50, 降温策略设置为T = 0.9T和T = 0.96T, 分析扰动函数1、2对反演结果的影响。反演参数见表 1, 定位结果见表 2。
| 表 1 反演参数 Table 1 Inversion parameters |
| 表 2 真实及反演定位结果 Table 2 Real and inverted earthquake locations |
将初始温度设置为1、25和50, 分别代入降温策略进行反演, 对比相同降温策略下(同为T = 0.9T或T = 0.96T)被接受模型的走时差二范数变化曲线, 结果见图 1。

|
图 1 被接受模型的走时差二范数变化曲线 Fig.1 The curves of the 2-norm of travel time differences for selected models |
由图 1可见, 3种初始温度设置对模型收敛影响不明显。同时, 由反演参数可知, 走时差二范数的值最终均收敛于Ecov = 1.44, 故认为1、25和50均为合理初始温度。
由表 2可知, 当初始温度改变时, 反演所得定位结果无明显差别。
3.2 扰动函数改变在每种温度条件下, 设置反演计算最多迭代200次, 以此选择合适的反演模型, 并按前述规则选择接受或不接受, 当模型被接受时就降温到下一个温度, 依此循环, 直至残差收敛。由反演参数(表 1)可知: ①对于扰动函数1、2, 当初始温度升高时, 被接受模型的总个数Nm也会增多; ②对比总迭代次数i与迭代中被接受模型的总个数Nm可知, 扰动函数1的迭代次数明显大于扰动函数2, 但2种情况下被接受模型的数量接近, 故扰动函数2比扰动函数1更高效。
由表 2可知, 扰动函数的改变对定位结果无明显影响。
3.3 降温策略改变将降温系数由0.9改变为0.96, 由反演参数(表 1)可知, 由于降温速率变慢, 相同初始温度下的迭代次数增加, 被接受模型的数量随之增加。
由表 2可知, 降温策略的改变, 对定位结果的影响并不显著。
4 实际地震定位2019年, 江苏省测震台网中心记录到本省及行政区界线外30 km以内ML≥1.8地震事件105次, 采用模拟退火算法, 对以上事件进行重新定位。根据对典型震例的试算分析, 在地震重定位反演中, 将初始温度设置为25, 使用效率较高的扰动函数2产生随机模型, 降温策略为T = 0.96T, 且设置低收敛阈值以保证模型收敛。将地震经纬度及深度反演结果与江苏省测震台网中心编目结果进行对比, 并计算误差。为清晰对比二者差别, 剔除定位结果中经纬度误差大于1°的4次黄海海域地震, 其余事件定位误差见图 2、图 3。
|
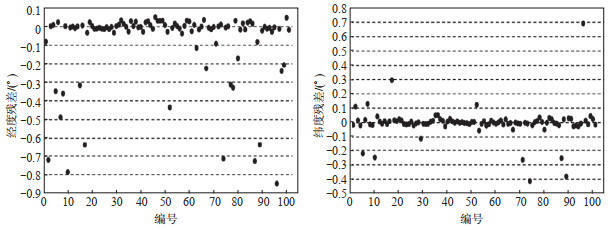
图 2 经、纬度坐标误差分布 Fig.2 Error distributions of Longitude and Latitude |
|
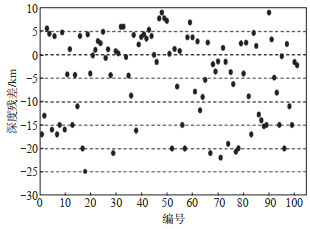
图 3 深度误差分布 Fig.3 Depth error distribution |
(1) 震中经、纬度坐标位置误差(图 2)。在105次地震中, 80次地震事件的经纬度坐标定位误差绝对值在0.1°以内, 占比约76%;25次地震事件定位误差大于0.1°, 其中海域地震19次, 陆地地震6次。
江苏东部临海且地震台站多建设在陆地上, 在对海域地震进行定位时, 可用台站偏于一侧, 在反演过程中, 模型范围的设置存在较大误差, 所以海域地震定位结果较差。对于6次误差大于0.1°的陆地地震, 可能是由于所使用含有效P波到时信息的台站数量少, 且台站空间分布较差, 未能较好地包围震中, 导致反演的震中位置结果误差较大。
(2) 震源深度误差(图 3)。在105次地震中, 31%的地震事件深度定位误差绝对值大于10 km, 由缺乏深度约束所致。
5 结论利用模拟退火算法, 对2019年江苏及邻区105次地震重新定位, 认为该算法对于江苏及邻区陆地地震的定位结果较为可信, 具体结论如下: ①选取典型震例进行反演试算, 通过设置不同的初始温度, 分析不同降温策略及在扰动函数1、2下的反演结果, 从而确定合适的反演参数; ②使用模拟退火算法进行地震定位反演时, 经度和纬度的反演结果较好, 由于缺乏深度约束, 定位深度有一定误差; ③模拟退火算法对P波到时信息多且地震台站分布较好的地震事件反演结果更优, 对可用台站偏向于震中一侧的海域地震而言, 因模型范围存在明显误差, 反演结果较差; ④对于江苏省测震台网中心记录的地震事件, 使用模拟退火算法进行地震定位反演, 大部分陆地地震事件重定位结果较为可信, 但海域地震事件的重定位结果可信度不足。
窦立婷, 成诚, 李云, 等. 利用模拟退火法反演大陆地震位置[J]. 地震地磁观测与研究, 2018, 39(1): 31-35. |
师学明, 王家映. 地球物理资料非线性反演方法讲座(三)模拟退火法[J]. 工程地球物理学报, 2007, 4(3): 165-174. DOI:10.3969/j.issn.1672-7940.2007.03.001 |
田玥, 陈晓非. 地震定位研究综述[J]. 地球物理学进展, 2002, 17(1): 147-155. |
杨波, 张炳, 隆爱军, 等. 模拟退火算法在地震定位中的应用[J]. 华北地震科学, 2019, 37(4): 73-77. |
尹奇峰, 潘冬明, 郭全仕, 等. 基于快速模拟退火算法的井中微地震事件定位反演[J]. 地球物理学进展, 2019, 34(5): 1954-1961. |
Billings S D. Simulated annealing for earthquake location[J]. Geophysical Journal International, 1994, 118(3): 680-692. DOI:10.1111/j.1365-246X.1994.tb03993.x |
Gao X, Wang W M, Yao Z X. Hypocentral determination using the simulated annealing method[J]. Chinese Journal of Geophysics, 2002, 45(4): 546-553. |
Geiger L. Probability method for the determination of earthquake epicenters from the arrival time only[J]. Bull St Louis Univ, 1912, 8: 60-71. |
Ingber L. Very fast simulated re-annealing[J]. Mathematical and Computer Modelling, 1989, 12(8): 967-973. |
Pishro-Nik H. Introduction to probability, statistics, and random processes[M]. Kappa Research LLC, 2014: 703-723.
|
Sen M K, Stoffa P L. Global optimization methods in geophysical inversion[M]. 2nd ed. Cambridge: Cambridge University Press, 2013: 81-117.
|
Van Laarhoven P J M, Aarts E H L. Simulated annealing: theory and applications[M]. Dordrecht: Springer, 1987: 99-135.
|
 2021, Vol. 42
2021, Vol. 42

