2. 中国北京 100081 中国地震局地球物理研究所
2. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China
1773年, 库仑(Coulomb, Charles Augustine, 1736—1806)提出破裂的最大剪切应力理论(Coulomb, 1785; Jeffreys, 1942, 1976). 他假设, 在应力作用下, 当脆性物质(例如岩石)中某一点的最大剪切应力达到某一确定值时, 就沿着最大剪切应力平面破裂。通常把这个值称为该物质的剪切强度(shear strength).
1849年, 霍普金斯(Hopkins)根据库仑提出的准则, 证明了破裂平面(即最大剪切应力平面)是通过中间主应力轴并平分最大与最小主应力轴之间的夹角的平面, 而作用于此平面上的剪切应力(最大剪切应力)等于最大与最小主应力之差的一半. 通常, 把最大主应力与最小主应力之差称为应力差(stress-difference). 应力差总为正值.
以p1, p2, p3代表脆性物质(例如岩石)中某一点的主应力[图 12(a)]. 若使用以主应力的方向为直角坐标系xi(i = 1, 2, 3)的坐标轴的方向, 过某一点取一个xi为常数的平面, 按弹性理论与地震学通常的习惯(Bullen, 1953; Jeffreys, 1976), 那么应力分量pik表示的是作用于该平面两侧的物质之间单位面积上, 并使xi较小一侧的物质朝xk增大方向位移的力. 因此, 若按照弹性理论与地震学通常的习惯, 主应力以张应力为正. 不过, 在把理论分析结果应用于地学问题, 特别是岩石力学、土力学、构造地质学时, 考虑到所涉及的正应力以压应力为主, 则通常把符号的规定反过来, 以压应力为正(Jaeger, 1962; Jeffreys, 1976; Jaeger and Cook, 1979; Atkinson, 1987; Turcotte and Shubert, 2001). 在以下分析中, 为避免混淆, 除非特别说明, 均按弹性理论与地震学通常的习惯, 以张应力为正.

|
图 12 最小主压应力轴(p1)、最大主压应力轴(p3)、破裂面法线方向(n)、滑动方向(e)和剪切破裂面之间的几何关系 (a) 破裂的最大剪切应力理论;(b) 安德逊理论 Fig.12 Minimum principal compressive stress axis (p1), maximum principal compressive stress axis (p3), normal direction of fracture surface (n), geometric relationship between slip direction (e) and shear fracture surface (a) Maximum shear stress theory of fracture; (b) Anderson theory |
设p1>p2>p3, 也就是说, p1, p2, p3依次是最大、中间、最小主(张)应力轴. 与主应力p1, p2, p3的方向相应的x1, x2, x3轴的方向依次称为最大、中间、最小主(张)应力轴方向. 若按岩石力学的规定, 则p1, p2, p3依次是最小、中间、最大主(压)应力轴. 与p1, p2, p3轴相应的方向依次称为最小、中间、最大主(压)应力轴方向.
今以ni(i = 1, 2, 3)表示某一平面的法线n的方向余弦, 以li和mi分别表示该平面上两条互相垂直的直线l和m的方向余弦. 以l, m, n构成一个右旋直角坐标系, 即以朝外的法线方向n的左方为l的正方向, 那么作用于该法线方向n的平面的应力矢量(stress-vector traction)pn为
| $ \boldsymbol{p}_{n}=\left(p_{1} n_{1}, \quad p_{2} n_{2}, \quad p_{3} n_{3}\right) . $ | (7) |
pn的法向分量即作用在该平面上的法向应力pnn, 则有
| $ p_{n n}=\boldsymbol{p}_{n} \cdot \boldsymbol{n}=p_{1} n_{1}^{2}+p_{2} n_{2}^{2}+p_{3} n_{3}^{2} ; $ | (8) |
而剪切应力在l和m方向的分量分别为pnl和pnm, 则有
| $ p_{n l}=\boldsymbol{p}_{n} \cdot \boldsymbol{l}=p_{1} n_{1} l_{1}+p_{2} n_{2} l_{2}+p_{3} n_{3} l_{3}; $ | (9) |
| $ p_{n m}=\boldsymbol{p}_{n} \cdot \boldsymbol{m}=p_{1} n_{1} m_{1}+p_{2} n_{2} m_{2}+p_{3} n_{3} m_{3}. $ | (10) |
在该平面内与l和m的夹角分别为ϕ和ϕ-(π/2)的方向上, 剪切应力为
| $ p_{n l} \cos \phi+p_{n m} \sin \phi . $ | (11) |
该剪切应力在
| $ \phi=\tan ^{-1}\left(\frac{p_{n m}}{p_{n l}}\right) $ | (12) |
时达极大值, 其数值p为
| $ p=\left(p_{n l}^{2}+p_{n m}^{2}\right)^{1 / 2}. $ | (13) |
由式(13)及式(9)与式(10)容易求得作用于该平面的最大剪切应力的数值p. 为书写简单起见, 给出该数值p的平方, 则有
| $ \begin{aligned} p^{2}=& p_{1}^{2} n_{1}^{2}\left(l_{1}^{2}+m_{1}^{2}\right)+2 p_{1} p_{2} n_{1} n_{2}\left(l_{1} l_{2}+m_{1} m_{2}\right) \\ &+p_{2}^{2} n_{2}^{2}\left(l_{2}^{2}+m_{2}^{2}\right)+2 p_{2} p_{3} n_{2} n_{3}\left(l_{2} l_{3}+m_{2} m_{3}\right) \\ &+p_{3}^{2} n_{3}^{2}\left(l_{3}^{2}+m_{3}^{2}\right)+2 p_{3} p_{1} n_{3} n_{1}\left(l_{3} l_{1}+m_{3} m_{1}\right) . \end{aligned} $ | (14) |
因为(l1, m1, n1), (l2, m2, n2), (l3, m3, n3)分别为p1, p2, p3轴在l, m, n坐标系中的方向余弦, 所以
| $ l_{1}^{2}+m_{1}^{2}+n_{1}^{2}=1, \quad l_{2}^{2}+m_{2}^{2}+n_{2}^{2}=1, \quad l_{3}^{2}+m_{3}^{2}+n_{3}^{2}=1, $ | (15) |
| $ l_{1} l_{2}+m_{1} m_{2}+n_{1} n_{2}=0, \quad l_{2} l_{3}+m_{2} m_{3}+n_{2} n_{3}=0, \quad l_{3} l_{1}+m_{3} m_{1}+n_{3} n_{1}=0. $ | (16) |
利用这些关系式, 可将p2表示为
| $ p^{2}=\left(p_{1}^{2} n_{1}^{2}+p_{2}^{2} n_{2}^{2}+p_{3}^{2} n_{3}^{2}\right)-\left(p_{1} n_{1}^{2}+p_{2} n_{2}^{2}+p_{3} n_{3}^{2}\right)^{2}, $ | (17) |
即
| $ p^{2}=\left|p_{n}\right|^{2}-p_{n n}^{2} . $ | (18) |
注意到
| $ n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1, $ | (19) |
则容易将p2表示成
| $ p^{2}=\left(p_{1}-p_{2}\right)^{2} n_{1}^{2} n_{2}^{2}+\left(p_{2}-p_{3}\right)^{2} n_{2}^{2} n_{3}^{2}+\left(p_{3}-p_{1}\right)^{2} n_{3}^{2} n_{1}^{2} . $ | (20) |
欲求最大剪切应力所在平面的法线方向n, 就是要求在
| $ g=1-\left(n_{1}^{2}+n_{2}^{2}+n_{3}^{2}\right)=0 $ | (21) |
所限制的条件下p2的极大值. 采用拉格朗日乘子法求p2取极大值的必要条件. 为此, 引进一个新的参量, 即拉格朗日乘子λ, 并定义一个新的函数F, 有
| $ F=p^{2}+\lambda g. $ | (22) |
由于g ≡ 0, 所以F取极值的条件也就是p2取极值的条件, 这些条件是
| $ \frac{\partial F}{\partial n_{1}}=0, \quad \frac{\partial F}{\partial n_{2}}=0, \quad \frac{\partial F}{\partial n_{3}}=0, \quad \frac{\partial F}{\partial \lambda}=0. $ | (23) |
由这些条件可以决定n1, n2, n3和λ. 将式(17)代入式(23), 由式(23)的最后一个条件给出式(21), 其余三个可以表示为
| $ \left\{\begin{array}{l} n_{1}\left(p_{1}^{2}-2 p_{n n} p_{1}-\lambda\right)=0, \\ n_{2}\left(p_{2}^{2}-2 p_{n n} p_{2}-\lambda\right)=0, \\ n_{3}\left(p_{3}^{2}-2 p_{n n} p_{3}-\lambda\right)=0. \end{array}\right. $ | (24) |
式中, n1, n2, n3至少有一个应当等于零, 如其不然, 则p1, p2, p3应满足同一个二次方程
| $ x^{2}-2 p_{n n} x-\lambda=0, $ | (25) |
然而二次方程至多只能有两个不等的根, 而不可能有三个不等的根p1, p2, p3. 这就导致了与p1>p2>p3的假设相矛盾的结论. 因此, n1, n2, n3中至少有一个等于零, 也就是说, 最大剪切应力平面应当通过某一主应力轴.
如果最大剪切应力平面通过p2轴, 即n2 = 0, 而n1, n3≠0, 那么由式(24)的第一与第三式可得
| $ \lambda=p_{3}^{2}-2 p_{n n} p_{3}=p_{1}^{2}-2 p_{n n} p_{1}, $ | (26) |
因此
| $ \left(p_{3}-p_{1}\right)\left[\left(p_{3}+p_{1}\right)-2 p_{n n}\right]=0 . $ | (27) |
既然p3≠p1, 则有
| $ p_{3}+p_{1}-2 p_{n n}=0 . $ | (28) |
将式(28)中的pnn用式(8)代入, 可得
| $ p_{3}\left(1-2 n_{3}^{2}\right)+p_{1}\left(1-2 n_{1}^{2}\right)=0 . $ | (29) |
由式(19)可知, 当n2 = 0时
| $ \left(1-2 n_{3}^{2}\right)+\left(1-2 n_{1}^{2}\right)=2-2\left(1-2 n_{2}^{2}\right)=0, $ | (30) |
则式(29)便简化为
| $ \left(p_{3}-p_{1}\right)\left(1-2 n_{3}^{2}\right)=0 . $ | (31) |
再次运用p3≠p1的条件, 可得
| $ n_{3}^{2}=n_{1}^{2}=\frac{1}{2} . $ | (32) |
把n2 = 0, n32=n12=1/2代入式(19), 则得到p2的最大值.
| $ n_{2}=0, \quad n_{3}^{2}=n_{1}^{2}=\frac{1}{2}, \quad p^{2}=\frac{\left(p_{3}-p_{1}\right)^{2}}{4} . $ | (33) |
若依次设n3 = 0及n1 = 0, 那么按照类似的步骤可以求得
| $ n_{3}=0, \quad n_{1}^{2}=n_{2}^{2}=\frac{1}{2}, \quad p^{2}=\frac{\left(p_{1}-p_{2}\right)^{2}}{4} . $ | (34) |
| $ n_{1}=0, \quad n_{2}^{2}=n_{3}^{2}=\frac{1}{2}, \quad p^{2}=\frac{\left(p_{2}-p_{3}\right)^{2}}{4} . $ | (35) |
既然p1>p2>p3, 所以只有式(33)给出的p才是数值最大的剪切应力值. 最大剪切应力平面的法向是
| $ \boldsymbol{n}=\left(\pm 2^{-1 / 2}, \quad 0, \quad \pm 2^{-1 / 2}\right) . $ | (36) |
如式(17), (20), (32), (36)诸式所表示的, n对于p1和p3轴均具有对称性, 因此只需分析
| $ \boldsymbol{n}=\left(2^{-1 / 2}, \quad 0, \quad 2^{-1 / 2}\right), $ | (37) |
一种情形. 此时, 若取
| $ \boldsymbol{m}=(0, \quad 1, \quad 0), $ | (38) |
| $ \boldsymbol{l}=\left(-2^{-1 / 2}, \quad 0, \quad 2^{-1 / 2}\right), $ | (39) |
则由式(8)—(10)可得
| $ p_{n l}=-\frac{p_{1}-p_{3}}{2}, p_{n n}=0, p_{n n}=\frac{p_{1}+p_{3}}{2} . $ | (40) |
这就是说, 最大剪切应力平面通过中间主应力轴并平分最大与最小主应力轴之间的夹角. 最大剪切应力的数值是最大与最小主应力之差的一半, 其作用方向在垂直于中等主应力轴并且位于剪切平面内的-l方向[图 12(a)].
既然n对于p1和p3轴有对称性, 则另一种情形(以p3轴为对称轴的情形)是
| $ \boldsymbol{n}=\left(2^{-1 / 2}, 0,-2^{-1 / 2}\right), $ | (41) |
| $ \boldsymbol{m}=(0,-1,0), $ | (42) |
| $ \boldsymbol{l}=\left(2^{-1 / 2}, 0,2^{-1 / 2}\right), $ | (43) |
| $ p_{n l}=\frac{p_{1}-p_{3}}{2}, p_{n m}=0, p_{n n}=\frac{p_{1}+p_{3}}{2} . $ | (44) |
上式所表示的结果即是与式(37)—(40)所表示的结果共轭的情形. 其他2种情形, 即n=(-2-1/2, 0, -2-1/2)与n=(-2-1/2, 0, 2-1/2)情形则分别与式(37)与式(41)给出的情形相同.
上述脆性破裂的最大剪切应力理论称为库仑—霍普金斯理论.
2.2 安德逊理论实验证明, 在单轴压力下, 脆性物质的破裂与库仑—霍普金斯理论预期的结果相符, p3轴与破裂面之间的夹角约为45°. 地震是地表面下岩石的破裂, 在地质条件下, 地表面下的岩石承受着其上方岩石重量引起的沉重的载荷, 也即高围压, 称为静岩压(lithostatic pressure). 许多证据表明, 在高围压下, 上述角度可减至20°—30°. 为解释这一现象, 安德逊(Anderson, 1905, 1942, 1951)将库仑—霍普金斯的理论加以修正, 他运用了库仑关于岩石脆性破裂的准则[图 12(b)]. 库仑准则亦称库仑—纳维(Navier)准则、纳维—库仑准则、库仑—莫尔(Mohr)准则, 但后三者与前者所涉及的物理背景实际上并不相同, 因此这里仍称之为库仑准则(Jaeger, 1962; Jaeger and Cook, 1979).
按照库仑准则, 岩石要发生破裂, 产生滑移, 除了要克服表征材料特征的内聚力以外, 还要克服与法向压应力(|pnn|)成正比的固体摩擦力的阻碍. 因此, 只有当作用于岩石中某一个面上的剪切应力达到剪切强度, 即内聚强度(cohesive strength)S和摩擦阻抗(µi|pnn|)之和时, 岩石才能沿着该平面发生脆性破裂, 也就是
| $ |p|=S+\mu_{i}\left|p_{n n}\right|, $ | (45) |
式中, µi是内摩擦系数(coefficient of internal friction). 地壳中大部分, 特别是地壳上部都有流体(主要是水)存在. 水和其他流体的存在影响断层的摩擦滑动. 在湿断层情况下, 式(45)中的压应力|pnn|应改为有效正应力(effective normal stress), 即破裂面上压应力|pnn|与孔隙压(pore pressure)pf的数值|pf|之差. 孔隙压即孔隙中的流体对断层的压强. 因此
| $ |p|=S+\mu_{i}\left(\left|p_{n n}\right|-\left|p_{\mathrm{f}}\right|\right). $ | (46) |
以水为例. 如果孔隙中的流体(水)与地表面是自由地连通的, 且无流动耗损, 则孔隙压即静水压, 有
| $ \left|p_{\mathrm{f}}\right|=\rho_{\mathrm{f}} g h, $ | (47) |
式中, ρf是流体(水)的密度, g是重力加速度, h是断层所在的深度. 设岩石的平均密度是ρ, 则岩石重量引起的载荷即静岩压, 有
| $ \left|p_{n n}\right|=\rho g h. $ | (48) |
因为水的密度比岩石的密度小得多, 所以静水压一般只是静岩压的35%至50%. 但是, 在某些情况下, 例如当水处于圈闭状态时, 孔隙压可能几乎等于甚而大于静岩压. 此时, 阻止断层运动的剪切应力很小.
若pnn是压力, |pnn| = -pnn; 若pnn是张力, |pnn| = pnn. 所以, 在干摩擦情况下, 有
| $ |p|=S \mp \mu_{i} p_{n n}. $ | (49) |
在上式以及以下的讨论中, 上、下方的符号(在上式中是+号)分别对应pnn是压力或张力的情形. 在干摩擦情况下, 为了求破裂平面的法向n, 需要求在式(21)所限制的条件下|p|±µipnn这个量的极大值, 在这里以及以下的讨论中, ±号分别对应pnn是压力或张力的情形. 与上节类似, 定义一个新的函数Φ, 则
| $ \varPhi=|p| \pm \mu_{i} p_{n n}+\lambda g, $ | (50) |
式中, λ是拉格朗日乘子, g仍如式(21)所示. 由于g ≡ 0, 所以Φ取极值的条件也就是|p|±µi pnn取极值的条件, 这些条件是
| $ \frac{\partial \varPhi}{\partial n_{1}}=0, \quad \frac{\partial \varPhi}{\partial n_{2}}=0, \quad \frac{\partial \varPhi}{\partial n_{3}}=0, \quad \frac{\partial \varPhi}{\partial \lambda}=0. $ | (51) |
上式表示的最后一个条件仍给出式(21), 其余三个条件可以表示为
| $ \left\{\begin{array}{l} n_{1}\left[\frac{p_{1}^{2}-2 p_{n n} p_{1}}{2|p|} \pm \mu_{i} p_{1}-\lambda\right]=0, \\ n_{2}\left[\frac{p_{2}^{2}-2 p_{n n} p_{2}}{2|p|} \pm \mu_{i} p_{2}-\lambda\right]=0, \\ n_{3}\left[\frac{p_{3}^{2}-2 p_{n n} p_{3}}{2|p|} \pm \mu_{i} p_{3}-\lambda\right]=0. \end{array}\right. $ | (52) |
与前面讨论库仑—霍普金斯理论的情况类似, n1, n2, n3应当至少有一个等于零. 若设n2 = 0, 而n3, n1≠0, 则由上式的第一与第三式可得
| $ \lambda=\frac{p_{1}^{2}-2 p_{n n} p_{1}}{2|p|} \pm \mu_{i} p_{1}=\frac{p_{3}^{2}-2 p_{n n} p_{3}}{2|p|} \pm \mu_{i} p_{3}, $ | (53) |
因此
| $ \left(p_{1}-p_{3}\right)\left[\left(p_{1}+p_{3}\right)-2 p_{n n} \pm 2 \mu_{i}|p|\right]=0 . $ | (54) |
因为p1≠p3, 所以
| $ \left(p_{1}+p_{3}\right)-2 p_{n n} \pm 2 \mu_{i}|p|=0 . $ | (55) |
将式(8)和式(19)代入上式, 可得
| $ p_{3}\left(1-2 n_{3}^{2}\right)+p_{1}\left(1-2 n_{1}^{2}\right) \pm 2 \mu_{i}\left|\left(p_{3}-p_{1}\right) n_{1} n_{3}\right|=0 . $ | (56) |
今以θ表示n与p1轴的夹角, 即n与最大主(张)应力轴(p1轴)的夹角(Scholz, 1990, 2002). 则
| $ \left\{\begin{array}{l} n_{1}=\cos \theta, \\ n_{3}=\sin \theta. \end{array}\right. $ | (57) |
按这里采用的定义, 在式(45)—(56)的分析中, 只涉及剪切应力的数值|p|, 因此在式(56)中, 改变n1或(和)n3的符号, 该式照样成立. 换句话说, n对于p1, p3轴都是对称的. 由于n对于p1和p3轴的对称性, 只需求0≤θ≤90°的解. 因此, 式(56)可以表示为
| $ \left(p_{1}-p_{3}\right)\left(\cos 2 \theta \mp \mu_{i} \sin 2 \theta\right)=0 . $ | (58) |
因为p1≠p3, 所以
| $ \tan 2 \theta=\pm \frac{1}{\mu_{i}} . $ | (59) |
这就是说, 当pnn是压应力即上式右边取正号时, 有
| $ \theta=\frac{1}{2} \tan ^{-1} \frac{1}{\mu_{i}} \text {, } $ | (60) |
而当pnn是张应力即式(59)右边取负号时, 有
| $ \theta=\frac{{\rm{ \mathit{ π} }}}{2}-\frac{1}{2} \tan ^{-1} \frac{1}{\mu_{i}} . $ | (61) |
此时, |p|±µi pnn达极大值, 也就是
| $ |p| \pm \mu_{i} p_{n n}=\frac{1}{2}\left(p_{1}-p_{3}\right) \sin 2 \theta \pm \mu_{i}\left(\frac{p_{1}+p_{3}}{2}+\frac{p_{1}-p_{3}}{2} \cos 2 \theta\right) . $ | (62) |
由式(59)可得
| $ \left\{\begin{array}{l} \sin 2 \theta=\frac{1}{\sqrt{1+\mu_{i}^{2}}}, \\ \cos 2 \theta=\pm \frac{\mu_{i}}{\sqrt{1+\mu_{i}^{2}}} . \end{array}\right. $ | (63) |
无论pnn是压应力还是张应力, sin2θ均由上式第一式表示, 而上式第二式的±分别对应于pnn是压应力与张应力情形. 所以
| $ |p|+\mu_{i} p_{n n}=\pm \frac{1}{2}\left[p_{1}\left(\mu_{i}+\sqrt{1+\mu_{i}^{2}}\right)+p_{3}\left(\mu_{i}-\sqrt{1+\mu_{i}^{2}}\right)\right] \quad\left(n_{2}=0\right). $ | (64) |
对于n3 = 0和n1 = 0的情形, 可以作类似的讨论. 在这两种情形下, 若以θ依次表示n与p2和n与p3轴的夹角, 可以求得
| $ |p|+\mu_{i} p_{n n}=\pm \frac{1}{2}\left[p_{2}\left(\mu_{i}+\sqrt{1+\mu_{i}^{2}}\right)+p_{1}\left(\mu_{i}-\sqrt{1+\mu_{i}^{2}}\right)\right] \quad\left(n_{3}=0\right) . $ | (65) |
| $ |p|+\mu_{i} p_{n n}=\pm \frac{1}{2}\left[p_{3}\left(\mu_{i}+\sqrt{1+\mu_{i}^{2}}\right)+p_{2}\left(\mu_{i}-\sqrt{1+\mu_{i}^{2}}\right)\right] \quad\left(n_{1}=0\right) . $ | (66) |
因为
| $ p_{1}\left(\mu_{i}+\sqrt{1+\mu_{i}^{2}}\right)>p_{2}\left(\mu_{i}+\sqrt{1+\mu_{i}^{2}}\right)>p_{3}\left(\mu_{i}+\sqrt{1+\mu_{i}^{2}}\right), $ | (67) |
| $ p_{3}\left(\mu_{i}-\sqrt{1+\mu_{i}^{2}}\right)>p_{2}\left(\mu_{i}-\sqrt{1+\mu_{i}^{2}}\right)>p_{1}\left(\mu_{i}-\sqrt{1+\mu_{i}^{2}}\right), $ | (68) |
这就证明了无论pnn是压应力还是张应力情形, 以
| $ \boldsymbol{n}=\left(\begin{array}{ll} \cos \theta, & 0, &\sin \theta \end{array}\right) $ | (69) |
为法向的平面是欲求的剪切破裂面. θ由式(60)(当pnn是压应力时)或式(61)(当pnn是张应力时)给出. θ是破裂面法向n与最大主(张)应力轴(p1轴即最小主压应力轴)的夹角, 也是剪切破裂面与最小主(张)应力轴(p3轴即最大主压应力轴)的夹角. 当µi = 0时, θ = π/4;当µi =1时, θ = π/8(pnn是压应力情形)或3π/8(pnn是张应力情形); 当µi→∞时, θ = 0(pnn是压应力情形)或π/2(pnn是张应力情形). 这就是说, 随着µi的增大, 对于pnn是压应力情形, 剪切破裂面的法向趋向最大主(张)应力轴, 剪切破裂面趋向最小主(张)应力轴(p3轴, 即最大主压应力轴)与中间主应力轴(p2轴)构成的平面. 这是很自然的. 在pnn是压应力情形, 压应力起着增加对剪切破裂的阻抗作用, 因此剪切破裂在主(压)应力轴与破裂面的夹角变小、剪切应力增加的情况下发生; 而在pnn是张应力情形, 张应力起着减小对剪切破裂的阻抗作用, 因此剪切破裂在主(压)应力轴与破裂面的夹角变大、剪切应力减小的情况下发生. 今取
| $ \boldsymbol{m}=(0,1,0), $ | (70) |
| $ \boldsymbol{l}=(-\sin \theta, 0, \cos \theta). $ | (71) |
则由式(8)—(10)可得
| $ p_{n l}=-\frac{p_{1}-p_{3}}{2} \sin 2 \theta, \quad p_{n m}=0, \quad p_{n n}=\frac{p_{1}+p_{3}}{2}+\frac{p_{1}-p_{3}}{2} \cos 2 \theta, $ | (72) |
| $ |p|+\mu_{i} p_{n n}=\frac{\mu_{i}}{2}\left(p_{1}+p_{3}\right)+\frac{1}{2}\left(p_{1}-p_{3}\right)\left(\sin 2 \theta+\mu_{i} \cos 2 \theta\right) . $ | (73) |
这就是说, 剪切破裂面是通过中间主应力轴并与最小主(张)应力轴(p3轴)成θ角的平面, 在该平面上剪切应力的数值为(1/2)(p1 - p3)sin2θ, 其作用方向在-l方向. 图 12(b)表示了p1, p3轴, n, 滑动方向e和破裂面之间的几何关系. 若以σ1>σ2>σ3依次表示最大、中间与最小主压应力轴, 则由于n对于σ1轴和σ3轴都有对称性, 所以有两个可能的破裂面, 它们都与σ1轴成θ的夹角.
破裂的安德逊理论与地质条件下地表面下岩石的破裂是相符的. 这是因为: 破裂一旦开始便是不连续的运动. 如果在张力的作用下发生破裂, 岩石的块体彼此脱离分开, 便无从发生摩擦. 如果岩石的块体不彼此脱离分开, 只要岩石块体相对滑移继续进行, 则摩擦力将成为岩石块体相对滑移的主要阻力. 因此, 库仑—霍普金斯理论适用于滑移起始时, 而安德逊的理论则可正确地决定滑移开始后的方向.
有许多证据表明, 深源地震也是岩石的破裂. 如果真是这样, 式(49)中的内摩擦系数µi一定随深度急遽地减小. 而根据式(60), θ就应趋于π/4, 即破裂面与主应力方向成45°角. 任何有关因体积变化而发生深源地震的假说都应符合极端应力近乎水平并且破裂面与竖直方向成45°角的结果.
2.3 地震断层在常温下, 若应力足够高, 岩石将发生脆性破裂. 在地球表面的岩石中, 可以看到许多类型的破裂. 如果沿破裂面发生侧向位移, 那么这个破裂就称为断层. 在地壳中有着各种尺度的断层, 尺度小的断层错距仅几毫米; 尺度大的断层有着由破碎了的岩石构成的宽阔地带, 称为断层泥带, 断层泥带的宽度可达数千米, 而断层的错距可达数百千米; 规模较小的断层的断层泥带宽度只有几厘米. 地震与许多断层的错动有关, 大地震的断层位错数量级为10 m, 最大可达数10 m.
刚性板块的相对运动通过大断层得到调整. 在海沟, 海洋岩石层板块沿下倾的断层面俯冲到邻接的海洋或大陆岩石层板块下, 两大板块的汇聚导致了俯冲作用以及世界上频繁发生的绝大多数的大地震. 通过这些规则地发生的地震, 连续的俯冲过程得到了调整.但这些断层的地面形迹在海沟底部, 比较难以进行详细的实地考察. 在发散带, 在大洋中脊边缘, 有许多正断层(normal fault). 因为在大洋中脊, 岩石层很薄, 所以由此导致的地震就比较小. 洋脊系中的分段的洋脊是通过转换断层连接起来的. 在转换断层上, 发生了黏滑作用. 转换断层在陆地上常有出露, 所以研究得比较多. 在大陆板块碰撞地带, 上述三种情形的断层都会出现. 我国大陆内部的许多大地震与印度板块和欧亚板块的碰撞所发生的大范围的形变地带有关; 土耳其强震活动也与这个碰撞带往西延续有关. 在大陆板块碰撞地带, 俯冲带以及转换断层, 地震的频度高、强度大. 在板块内部, 也发生大地震, 不过频度低一些.
由上述情况可知, 有三种基本类型的断层: 逆断层(reverse fault), 走滑断层(strike-slip fault)和正断层(normal fault). 这三种断层的发生是由主应力轴在空间的取向决定的(Jaeger, 1962; Jaeger and Cook, 1979; Turcotte and Schubert, 2001).
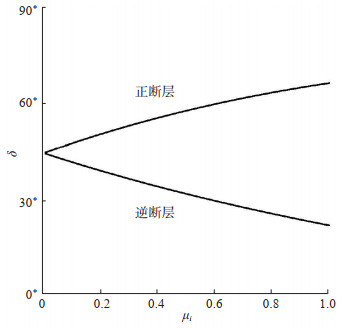
2.3.1 逆断层如果p1轴垂直于地面, p2和p3轴平行于地面, 则破裂面过p2轴并与p3轴成θ角, 0°<θ<45°, 这种断层称为逆断层, 也称为逆滑断层(reverse-slip fault)或压性断层(compressional fault). 如图 13(a)所示, 有两个断层面共轭的逆断层, 其断层面的倾角δ都等于θ. 断层面的倾角的取值范围是0°≤δ ≤45°. 随着摩擦系数由零开始增加, δ由45°逐渐减小(图 14).

|
图 13 地震断层 (a) 逆断层; (b) 走滑断层; (c) 正断层 Fig.13 Earthquake faults (a) Reverse fault; (b) Strike slip fault; (c) Normal fault |
|
图 14 正断层和逆断层的断层面倾角δ与内摩擦系数μi的关系 Fig.14 Relationship between dip angle δ of fault plane and internal friction coefficient μi of normal fault and reverse fault |
为了确定内摩擦系数µi, 不但在野外对地质断层做了许多观测, 而且在实验室内对各种岩石做了测量(Byerlee, 1967, 1968, 1977, 1978). 结果表明, µi是数量级为1的量, 通常介于0.5和1.0之间. 图 15是各种不同类型的岩石开始摩擦滑动时的最大剪切应力p与正应力|pnn|的关系图, 除了一些表示滑动面之间充塞着断层泥的岩石的数据点外, 结果比较集中: 当正应力低于相当于地壳中部深度的正应力数值200 MPa(2 kbar)即|pnn|<200 MPa时, 有

|
图 15 各种不同类型的岩石开始摩擦滑动时的最大剪切应力(p)与正应力(|pnn|)的关系 Fig.15 The relationship between the maximum shear stress (p) and the normal stress (| pnn |) at the beginning of frictional sliding of different types of rocks |
| $ p=0.85\left|p_{n n}\right|,$ | (74a) |
当200 MPa<| pnn |<1 700 MPa时, 有
| $ p=50+0.6\left|p_{n n}\right|. $ | (74b) |
上式称为拜尔理定律(Byerlee, 1978). 在这个公式中, 最大剪切应力p和正应力的数值|pnn|均以MPa为单位, 1 MPa = 10 bar. 若以kbar为单位, 则式(74b)等号右边第一项的常数应改为0.5. 对于式(74a)所表示的µi = 0.85的情形, 逆断层的倾角δ = 24.8°; 对于式(74b) 所表示的µi = 0.6的情形, 逆断层的倾角δ = 29.5°。
2.3.2 走滑断层如果p2轴垂直于地面, p3与p1轴平行于地面, 则图 13(b)所示的两个共轭的断层面都与p3轴成θ角.这种断层称为走滑断层(strike-slip fault), 也称为横推断层(transcurrent fault)、横断层(lateral fault)、捩断层(tear fault)或扭断层(wrench fault). 走滑断层的倾角δ常接近于90°. 对于走滑断层情形, p1可以是数值比p2和p3都小的压应力, 也可以是张应力.
走滑断层分为右旋走滑断层(dextral strike-slip fault, right-lateral slip fault)和左旋走滑断层(sinistral strike-slip fault, left-lateral slip fault). 走滑断层是右旋还是左旋可以用下述方法判别: 站在断层的一盘沿着与断层走向垂直的方向观看另一盘的运动, 若该盘向右运动则断层为右旋走滑断层[图 13(b)右图中的断层AB], 若该盘向左运动则断层为左旋走滑断层[图 13(b)右图中的断层CD].
2.3.3 正断层在地下某一深度处, 竖直方向的主应力可能变成最大主压应力, 即最小主(张)应力轴(p3)轴垂直于地面. 此时, 破裂面与垂线的夹角等于θ [图 13(c)]. 这种断层称为正断层, 也称为正滑断层(normal fault), 张性断层(tensional fault)或重力断层(gravity fault). 如图 13(c)所示, 正断层的断层面的倾角δ = 90°- θ, 其取值范围为45°<δ<90°. 随着内摩擦系数由零增加, δ由45°逐渐增加. 若µi = 0.85, 正断层的倾角δ = 65.2°, 逆断层的倾角δ = 24.8°; 若µ = 0.6, 正断层的倾角δ = 60.5°, 逆断层的倾角δ = 29.5°. 正断层和逆断层统称倾滑断层(dip-slip fault). 由于正断层的断层面的倾角δ = 90°-θ, 而因为0°<θ<45°, 所以45°<δ<90°; 而逆断层的断层面的倾角δ = θ, 0°<δ<45°, 所以正断层的断层面要比逆断层的陡峭[图 13(a), (c)及图 14]. 倾滑断层是正断层还是逆断层是由断层面上方的地块即上盘(hanging wall block)相对于下方的地块即下盘(foot wall block)的运动是向下[图 13(c)]还是向上[图 13(a)]确定.
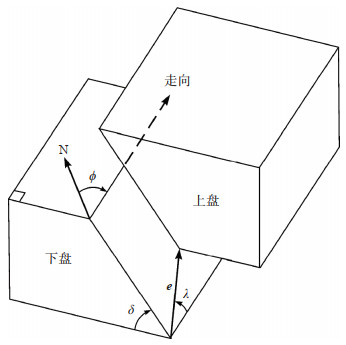
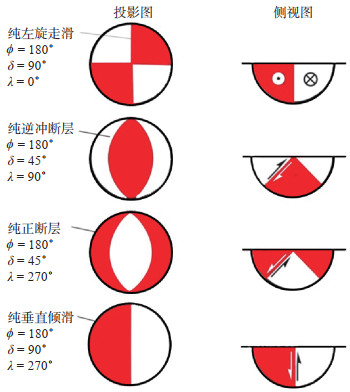
2.3.4 斜滑断层实际情况要比上述三种情形复杂, 一般的断层兼有走滑和倾滑两种分量(图 16). 如果断层面上的走向滑动和倾向滑动的分量都很明显, 则称这种断层为斜向滑动断层(oblique fault), 简称斜滑断层, 相应的滑动称为斜滑(oblique slip). 断层面两侧的地块的运动可以用滑动矢量e描述. 滑动矢量是表示断层的上盘相对于下盘的运动方向的单位矢量. 对于剪切滑动来说, 滑动矢量可以位于断层面上的任何方向上。滑动矢量与断层面走向的夹角λ称为滑动角(slip angle或rake angle, 分别简称为slip或rake)。断层面走向(strike)是断层面与地面的交线, 它有两个方向, 相差180°。为明确起见, 规定选取站在上盘向右看的方向为断层面走向。这样一来, 断层面的倾向(dip direction)比断层面的走向恒大90°, 一旦说明了断层面的走向ϕ, 0°≤ϕ<360°, 便意味着断层面的倾向是ϕ + 90°。当倾角δ = 90°时, 断层面的走向以及上盘与下盘的选取原则上是任意的。但是, 为明确起见, 规定先任选两个方向中的一个方向为断层面的走向, 一旦选定, 便以沿该方向朝前看时右手边的那一盘为“上盘”。规定0°≤λ<360°, 逆时针为正(Ben-Menahem and Singh, 1981, p.183)。有的作者(Aki and Richards, 1980, p.106; Lay and Wallace, 1995)则规定-180°<λ ≤180°, 显然, 这两种规定并无本质差别。随着λ由0°逆时针增至360°, 相应的剪切滑动断层的地质学术语如表 1所示。有时, 又将倾角σ<45°的逆断层特别称为冲断层(thrust fault), 将δ<10°的逆断层特别称为上冲断层或逆冲断层(overthrust fault)。作为举例, 图 17以震源球下半球等面积投影表示走向为N-S方向(ϕ = 0°), 倾角为45°(δ = 45°)的断层面当滑动角λ由0°增至330°时震源机制解所表示的断层滑动类型的变化。图中, 黑色区域表示初动为压缩(+)的区域, 白色区域表示初动为膨胀(-)的区域。以这种投影图的方式表示的震源机制解(断层面解)在西方形象地称为“海滩球(beach ball)”或“沙滩球”, 在我国则形象地称为“西瓜皮”。图 18则以投影图即“海滩球”或“西瓜皮”(左图)和侧视图(右图)表示走向为N-S方向(ϕ = 180°), 倾角δ = 45°的几种震源机制解(Ben-Menahem and Singh, 1981; Stein and Wysession, 2003)。
|
图 16 斜滑断层 图中表示断层面的走向ϕ, 倾向ϕ + 90°, 倾角δ, 断层的上盘, 下盘, 滑动矢量e, 滑动角λ Fig.16 Oblique fault The figure shows the strike ϕ, dip direction ϕ + 90°, dip angle δ, the hanging and foot wall blcoks, slip vector e and slip angle λ of fault plane |
| 表 1 剪切滑动断层的地质学术语 Table 1 Geological terminology of shear slip fault |

|
图 17 与各种不同的滑动角相应的地震的震源机制解 当λ = 0°, …, 90°, …, 180°, …, 270°, …, 330°时, 由N-S节面(ϕ = 0°, σ = 45°的节面)所表示的震源机制, 由纯左旋走滑断层(λ = 0°), 变至纯逆冲断层(λ =90°), 变至纯右旋走滑断层(λ = 180°), 变至纯正断层(λ = 270°), 变至以走滑为主的左旋—正断层(λ = 330°) Fig.17 Focal mechanism for earthquakes with the same N-S striking fault plane (nodal plane ϕ = 0°, δ = 45°), but with slip angles varying from pure left lateral strikeslip (λ = 0°), to pure reverse dip-slip (λ = 90°), to pure right lateral strike-slip (λ = 180°), to pure normal dip-slip (λ = 270°), to mostly left lateral strike-slip with some normal dip-slip (λ = 330°) |
|
图 18 几种地震震源机制解投影图(左图)与侧视图(右图) Fig.18 Projection of solutions of several seismic source mechanisms (left) and side view (right) |
Aki K and Richards P G. Quantitative Seismology: Theory and Methods, 1 & 2[M]. San Francisco: W. H. Freeman, 1980: 1-932.
|
安芸敬一, P. G. 理查兹. 定量地震学. 第1, 2卷[M]. 李钦祖, 邹其嘉, 等译. 北京: 地震出版社, 1986: 1-620, 1-406.
|
Anderson E M. Dynamics of faulting[J]. Trans Geol Soc Edinburgh, 1905, 8: 387-402. DOI:10.1144/transed.8.3.387 |
Anderson E M. The Dynamics of Faulting and Dyke Formation with Application to Britain[M]. 2nd edition. Edinburgh: Oliver and Boyd, 1951: 1-206.
|
Anderson E M. The Dynamics of Faulting[M]. London: Oliver and Boyd, 1942: 1-183.
|
Atkinson B K. Fracture Mechanics of Rock[M]. London: Academic Press, 1987: 1-534.
|
Ben-Menahem A and Singh S J. Seismic Waves and Sources[M]. New York: Springer-Verlag, 1981: 1-1 108.
|
Bullen K E. An Introduction to the Theory of Seismology[M]. 2nd edition. Cambridge: Cambridge University Press, 1953: 1-296.
|
K E布伦著. 地震学引论[M]. 朱传镇, 李钦祖译, 傅承义校. 北京: 科学出版社, 1965: 1-336.
|
Byerlee J D. Brittle-ductile transition in rocks[J]. J Geophys Res, 1968, 73: 4741-4750. DOI:10.1029/JB073i014p04741 |
Byerlee J D. Friction of rocks[C]//Proc. Conf. II Experimental Studies of Rock Friction with Application to Earthquake Prediction, USGS, 1977: 55-77.
|
Byerlee J D. Friction of rocks[J]. Pure Appl Geophys, 1978, 116: 615-626. DOI:10.1007/BF00876528 |
Byerlee J D. Frictional characteristics of granite under high confining pressure[J]. J Geophys Res, 1967, 72: 3639-3648. DOI:10.1029/JZ072i014p03639 |
Coulomb C A. Theorie des Machines Simples//Memoires de Mathématique et de Physique de l'Académie Royale des Sciences, 1785: 161.
|
Jaeger J C and Cook N G W. Fundamentals of Rock Mechanics[M]. 3rd edition. London: Chapman and Hall, 1979: 1-593.
|
Jaeger J C. Elasticity, Fracture and Flow, with Engineering and Geological Applications[M]. 2nd edition. London: Methuen, 1962: 1-212.
|
Jeffreys H. On the mechanics of faulting[J]. Geol Mag, 1942, 79: 291-295. DOI:10.1017/S0016756800076019 |
Jeffreys H. The Earth: Its Origin, History, and Physical Constitution[M]. 6th edition. Cambridge: Cambridge University Press, 1976: 1-574.
|
H. 杰弗里斯. 地球: 它的起源、历史和物理组成[M]. 张焕志, 李致森译. 北京: 科学出版社, 1985: 1-437.
|
Lay T, Wallace T C. Modern Global Seismology[M]. New York: Academic Press, 1995: 1-521.
|
Stein S, Wysession M. An Introduction to Seismology, Earthquakes, and Earth Structure[M]. Malden, MA: Blackwell Publishing, 2003: 1-498.
|
Turcotte D L, Schubert G. Geodynamics[M]. 4th edition. Cambridge: Cambridge University Press, 2001: 1-456.
|
 2021, Vol. 42
2021, Vol. 42
