2. 中国昆明 650224 云南省地震局
2. Yunnan Earthquake Agency, Kunming 650224, China
地震发生受到构造运动控制(中国科学院地质研究所,1997),构造运动伴随着岩石圈磁场的变化,岩石圈磁场及其变化是地球深部物理过程的重要信息来源之一(丁鉴海等,1994)。地磁总强度数据通过日变通化、长期变改正处理后剥离得到岩石圈磁场,岩石圈磁场位场分离后得到地壳深部、浅表和居里面的能量加卸载信息,直接反映了地球内部各深度的物理过程和构造活动能量,比较真实可靠。但获取的地磁总强度数据是离散分布的点位,而实际采集的数据点位有限,难以直观反映岩石圈磁场变化,进而不利于判定岩石圈磁场异常区,需要对岩石圈磁场数据进行网格化处理。网格化数学模型的好坏不但影响到网格化岩石圈磁场数据的精度和可信程度,而且会进一步影响解释处理图件的质量、效果和可靠性。常用网格化数学模型有最小曲率、克里格、改进Shepard、反距离加权和径向基函数等(李振海等,2010)。文中将以上5种数学模型应用于小江断裂带岩石圈磁场数据网格化,并采用实验方法对其精度进行比较分析。
1 数学模型基本原理 1.1 最小曲率最小曲率法用公式表示为
| $ \left\{\begin{array}{l} \nabla^{2}\left(\nabla^{2} z\right)=\sum\limits_{i} f_{i} \delta\left(x-x_{i}, y-y_{i}\right) \\ \frac{\partial^{2} z}{\partial n^{2}}=0, \frac{\partial^{2}}{\partial n}\left(\nabla^{2} z\right)=0, \quad \frac{\partial^{2} z}{\partial x \partial y}=0 \end{array}\right. $ | (1) |
式中,∂/∂n表示对边界取法向导数(Smith et al,1990)。
1.2 克里格克里格模型根据所给数据趋势,构造一个只与点间空间距离相关的半方差函数,从而求取各拟合点的权系数,据此进行数值内插(刁鑫鹏等,2012)。
对于区域化变量Z(xi, yi),假设在n个位置取样,有Z(x1, y1),Z(x2, y2),…,Z(xn, yn),则点(xp, yp)处的估计量为
| $ Z\left(x_{p}, y_{p}\right)=\sum\limits_{i=1}^{n} \lambda_{i} Z\left(x_{i}, y_{i}\right) $ | (2) |
式中,λi为待定克里格权系数,为满足无偏、方差最小的条件,需
| $ \left\{\begin{array}{l} \sum\limits_{i=1}^{n} \lambda_{i}=1 \\ \sum \lambda_{i} \gamma\left(x_{i}, x_{j}\right)+\mu=\gamma\left(x_{0}, x_{i}\right) \end{array}\right. $ | (3) |
式中,μ为拉格朗日乘子,γ(xi, xj)为变异函数。求出λi便可求得未采样点值。
理论变异函数模型较多,常用线性模型、指数模型、高斯模型和球面模型等(Pan,1997)。
1.3 改进ShepardShepard是一种改进的加权平均法,采用1964年提出的局部逼近模型,以R为半径的拟合区分为2个环带,并分别定义权函数(管泽霖等,1994)。
| $ p(r)= \begin{cases}\frac{1}{r_{i}} & 0<r_{i} \leqslant \frac{R}{3} \\ \frac{27}{4 R}\left(\frac{r_{i}}{R}-1\right) & \frac{R}{3}<r_{i} \leqslant R \\ 0 & R<r_{i}\end{cases} $ | (4) |
式中,ri为已知点与待定点之间的平面距离。
| $ r_{i}=\sqrt{\left(B-B_{i}\right)^{2}+\left(L-L_{i}\right)^{2}} $ | (5) |
拟合数学模型为
| $ \zeta(x, y)= \begin{cases}\frac{\sum\limits_{i=1}^{n} f_{i}\left(p\left(r_{i}\right)\right)^{\mu}}{\sum\limits_{i=1}^{n}\left(p\left(r_{i}\right)\right)^{\mu}} & r_{i} \neq 0 \\ f_{i} & r_{i}=0\end{cases} $ | (6) |
反距离加权的基本思想是将权函数看作距离倒数的二次方(郑晓月等,2008),则
| $ Z(x, y)= \begin{cases}\frac{\sum\limits_{i=1}^{n}\left(d_{i}\right)^{-2} Z_{i}}{\sum\limits_{i=1}^{n}\left(d_{i}\right)^{-2}}& d_{i} \neq 0 \\ Z_{i} & d_{i}=0\end{cases} $ | (7) |
式中,Z(x, y)表示坐标点(x, y)上的插值结果;Zi为第i个点的已知值;di为第i点与插值点之间的距离。
1.5 径向基函数径向基函数是多个数据网格化方法的组合,其基函数由单个变量的函数构成(陈欢欢等,2007),一个点(x, y)的基函数形式往往是hi(x, y)=h(di),其中di表示由点(x, y)到第i个数据点的距离。基函数类型有如下几种。
(1)倒转复二次函数,公式如下
| $ B(h)={}^{1}\!\!\diagup\!\!{}_{\sqrt{{{h}^{2}}\times {{R}^{2}}}}\; $ | (8) |
(2)复对数,公式如下
| $ B(h)=\lg \left(h^{2}+R^{2}\right) $ | (9) |
(3)复二次函数,公式如下
| $ B(h)=\sqrt{h^{2} \times R^{2}} $ | (10) |
(4)自然三次样条函数,公式如下
| $ B(h)=\left(h^{2}+R^{2}\right)^{3 / 2} $ | (11) |
(5)薄板样条法函数,公式如下
| $ B(h)=\left(h^{2}+R^{2}\right) \lg \left(h^{2}+R^{2}\right) $ | (12) |
数学模型精度的检验方法主要有交叉验证和验证方法(杨元德等,2013),即预留一个或多个数据样本点,对预留数据点进行预测,计算所有估计值与实际值的误差,以此来判断估值方法的优劣。交叉验证的原理是:使用全部数据评价自相关模型,逐一删除每个数据点,并预测被删除点的值。验证方法的原理是:删除部分数据(称之为验证数据),使用剩余数据研究趋势及预测的自相关模型。
综上,选取采样点计算的均方根预测误差(RMSPE,Root Mean Square Predictive Error)来评定各种插值方法的精度,其值越小说明插值结果越接近真实值,结果越可靠;使用插值数据残差均方根(RMS)来评价网格数据与插值数据的一致性。
均方根预测误差的计算式为
| $ \mathrm{RMSPE}=\sqrt{\frac{1}{k} \sum\limits_{j=1}^{k}\left(z_{j}-z_{j}^{\prime}\right)^{2}} $ | (13) |
式中,k表示用于估计网格数据精度的样本数,zj表示第j(1≤j≤k)个样点插值后的值,z′j表示第j个样点实测值。
插值数据残差均方根计算式为
| $ \mathrm{RMS}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(z_{i}-z_{i}^{\prime}\right)^{2}} $ | (14) |
式中,n表示全部用于插值的样本数据点数,zi表示第i个点插值后的值,z'i表示第i点的实测值。
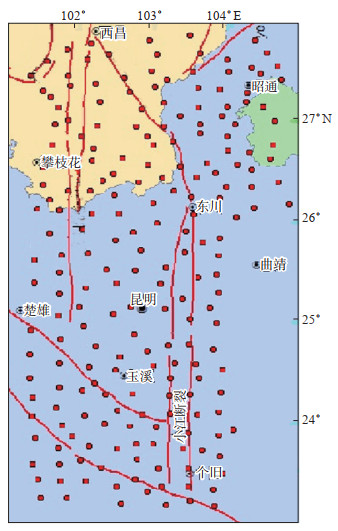
2.2 实验数据小江断裂地磁总强度加密区纬度跨度约23°-28°,经度跨度约101°-104°,测点间距约25 km,共布设了216个测点。选取该测区2017年和2018年各2期岩石圈磁场数据作为本文的实验数据。测点分布和实验数据信息见图 1和表 1。
|
图 1 小江断裂总强度加密区测点分布 Fig.1 Distribution of measuring points in the total intensity of Xiaojiang fault |
| 表 1 小江断裂总强度加密区数据信息 Table 1 Data information on the total intensity of the Xiaojiang fault |
对表 1中每一期地磁总强度数据进行预处理,剔除变迁测点和孤立异常点数据。对预处理后的总强度数据进行日变通化改正和长期变改正,用长期变改正得到的磁场数据减去国际地磁参考场模型数据得到岩石圈磁场数据。由于每期数据独立测量,实验数据不具有相关性。选用均方根预测误差(RMSPE)和插值数据残差均方根(RMS)等评定指标,对5种数学模型的网格化数据结果进行精度评定,评定结果见表 2-表 5。结果表明:①克里格与反距离加权插值方法的数据网格化精度优于最小曲率、径向基函数和改进Shepard等3种插值方法;②克里格与反距离加权插值方法的数据网格化精度相当,2种插值方法均可用于岩石圈磁场数据的网格化。
| 表 2 2017年3月数据不同数学模型精度评定结果(单位:nT) Table 2 Data accuracy of different mathematical model assessment results in March 2017(Unit: nT) |
| 表 3 2017年8月数据不同数学模型精度评定结果(单位:nT) Table 3 Data accuracy of different mathematical model assessment results in August 2017(Unit: nT) |
| 表 4 2018年3月数据不同数学模型精度评定结果(单位:nT) Table 4 Data accuracy of different mathematical model assessment results in March 2018(Unit: nT) |
| 表 5 2018年8月数据不同数学模型精度评定结果(单位:nT) Table 5 Data accuracy of different mathematical model assessment results in August 2018(Unit: nT) |
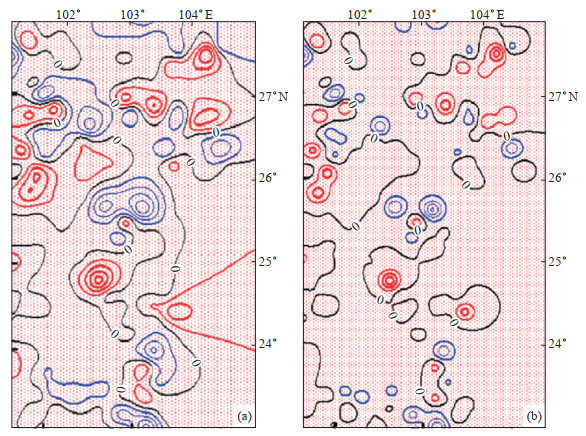
进一步从网格化图形质量、数据点位空间相关性等结果来比较克里格插值与反距离加权插值法的优劣。如图 2所示,反距离加权插值主要考虑数据的光滑性,而数据点位空间相关性不足,网格化结果失真;相反,克里格插值网格化图形平滑,能更好反映数据点的空间相关性,岩石圈磁场变化的分布和大小特征明显,克里格插值优于反距离加权插值法。
|
图 2 2018年3月小江断裂岩石圈磁场数据克里格插值和反距离加权插值结果 (a)克里格插值;(b)反距离加权插植 Fig.2 The meshing results of the Kriging model and inverse distance weighted method for the magnetic field data of the Xiaojiang fault in March 2018 |
通过比较小江断裂地磁总强度加密区岩石圈磁场数据的格网化结果可以发现,克里格与反距离加权插值的数据网格化精度优于最小曲率、径向基函数和改进Shepard等插值方法;克里格插值方法的网格化数据精度略优于反距离加权插值方法。进一步从网格化图形质量、数据点位空间相关性等结果来比较克里格插值与反距离加权插值法的优劣。结果表明克里格插值兼顾数据平滑性和各实测点与待估点之间的空间位置关系,并较好利用已有实测数据空间分布的结构特征,避免了系统误差,岩石圈磁场变化的分布和大小特征明显,得出克里格插值是岩石圈磁场数据网格化的最优数学模型的结论。
陈欢欢, 李星, 丁文秀. Surfer8.0等值线绘制中的十二种插值方法[J]. 工程地球物理学报, 2007, 4(1): 52-57. |
刁鑫鹏, 吴侃. 基于Kriging算法与曲面拟合的三维激光扫描点云数据插值研究[J]. 大地测量与地球动力学, 2012, 32(1): 110-113. |
丁鉴海, 卢振业, 黄雪香, 等. 地震地磁学[M]. 北京: 地震出版社, 1994: 97-98.
|
管泽霖, 李建成, 晁定波, 等. WZD94中国重力大地水准面研究[J]. 武汉测绘科技大学学报, 1994, 19(4): 292-297. |
李振海, 汪海洪. 重力数据格网化方法比较[J]. 大地测量与地球动力学, 2010, 30(1): 140-144. |
杨元德, 熊云琪, 王泽民, 等. 几种插值方法在构建南极DEM中的比较[J]. 大地测量与地球动力学, 2013, 33(5): 63-66. |
郑晓月, 康锟鹏. 一种基于加权平均的曲面拟合算法在电法勘探中的应用[J]. 河南理工大学学报(自然科学版), 2008, 27(1): 106-108. |
中国科学院地质研究所. 中国地震地质概论[M]. 北京: 科学出版社, 1997: 53-54.
|
Pan Guocheng. Geostatistical analysis of the structure of the theory and methods[J]. Global Geology, 1997, 16(3): 70-82. |
Smith W H F, Wessel P. Gridding with continuous curvature splines in tension[J]. Geophysics, 1990, 55(3): 293-305. |
 2021, Vol. 42
2021, Vol. 42
