2. 中国郑州 450000 中国地震局地球物理勘探中心;
3. 中国乌鲁木齐 830011 新疆维吾尔自治区地震局;
4. 中国海口 570203 海南省地震局
2. Geophysical Exploration Center, China Earthquake Administration, Zhengzhou 450000, China;
3. Earthquake Agency of Xinjiang Uygur Autonomous Region, Urumqi 830011, China;
4. Hainan Earthquake Agency, Haikou 570203, China
地震灾害发生之后,对地震成灾范围、人员伤亡和经济损失等快速估计,统称为地震灾害快速评估。地震灾害快速评估是地震应急决策辅助建议的重要基础和科学依据(杨天青等,2006)。
“九五”以来,中国先后有20余个城市和地区开展了震害预测工作,并各自建立了防震减灾信息管理与辅助决策系统(GB/T 19428-2003地震灾害预测及其信息管理系统技术规范)。“十五”期间,以震害预测研究成果为基础,基本实现了覆盖中国大陆的全国一体化地震应急指挥技术系统网络(帅向华等,2009),形成了国家、区域、城市三级地震应急指挥体系。这些震害快速评估系统或震害预测系统的工作原理是,在观测到地震发生时间、地点和震级后,未达地震现场调查前,利用对应地区地震烈度衰减关系给出震区不同烈度分布及影响范围,并快速估算地震灾害损失,提出地震应急决策和救援方案,供抗震救灾指挥部决策使用。此烈度分布确定的偏差程度决定了整个系统的可靠程度(许卫晓等,2012)。
中国幅员辽阔,历史地震资料丰富,研究者对不同地区、不同地质构造环境的地震烈度衰减关系进行了研究,得出了各研究区统计关系,例如:汪素云等(2000)将中国大陆以105°E分为东部和西部2个区,并确定两区地震烈度衰减关系;崔鑫等(2010)使用20世纪华南地区48次中强地震事件96条等震线数据,拟合得到华南地区地震烈度衰减关系;王继等(2008)收集了1991-2006年华中、华南25次地震的烈度分布图,配合1918-1989年9次地震烈度分布图,重新拟合两区地震烈度衰减关系。利用这些烈度衰减关系,可对相应地区将来发生的某次地震进行烈度分布评估,并对初评结果的偏差程度进行深入研究。
通常,地震烈度衰减关系受震源特性、深部构造、传播介质、场地条件、建筑物结构类型和居民点分布、地形等因素的影响,存在较大地区差异(汪素云等,2000)。为此,选取我国大陆地区发生的中强地震,建立西部(西北地区、西南地区)、东部(华北、东北地区、华中、华南地区)地区的地震烈度衰减关系,并就某些强震震例进行烈度分布评估,对其偏差特性和一般趋势进行分析,旨在研究利用烈度衰减关系进行烈度分布评估的一般规律。
1 我国大陆地区椭圆地震烈度衰减关系的建立 1.1 震例选取可依据以下原则选取震例烈度资料:①震例数据来源可靠;②震例等震线分布图清晰;③等震线图中参考点较充分,可准确地进行地理坐标配准和数字化;④烈度I和震级MS独立测定,以降低烈度I和震级MS之间相关性。
文中资料主要取自《中国近代地震目录(公元1912-1990年)》(中国地震局震害防御司,1999)、《中国地震灾害损失资料汇编(1966-1989)》(国家地震局震灾应急救援司,2015)、《中国震例1966-2007》、(中国地震局监测预报司,2001)、《中国大陆地震灾害损失汇编(2001-2005)》(中国地震局震灾应急救援司,2010)、《中国大陆地震灾害损失汇编(2006-2010)》(中国地震局震灾应急救援司,2015)、中国地震局网站及相关文献等。基于以上原则,选取1900年以来我国大陆西部地区4.0级以上震例488个,东部地区4.0级以上震例182个,分区统计结果见表 1。
| 表 1 1900年以来我国震例统计 Table 1 The earthquakes on the Chinese mainland since 1900 |
沿用中国地震烈度区划图的做法,以105°E为界,将中国大陆地区划分为东部和西部2个区(汪素云等,2000)。中国西部进一步细分为西南及西北2个子区域,其中:西南地区指中国西南部广大腹地,包括青藏高原东南部、四川盆地、云贵高原等,研究区域包括:四川、贵州、云南、西藏、重庆、广西;西北地区指大兴安岭以西,昆仑山-阿尔金山、祁连山以北广大地区,研究区域包括:陕西、甘肃、青海、内蒙古(105°E以西)、宁夏、新疆。中国东部进一步细分为华北、东北及华中、华南2个子区域(汪素云等,2000),其中华北、东北地区范围大体包括华北、辽东地区以及渤海和黄海大部,北至大青山,西至六盘山,南至大别山,研究区域包括:北京、天津、河北、山西、辽宁、吉林、黑龙江、山东、河南、内蒙古(105°E以东)(崔鑫等,2010);华中、华南地区包括:上海、江苏、浙江、安徽、福建、江西、湖北、湖南、广东、海南(王继等,2008)。
1.3 地震烈度衰减模型受发震构造的影响,我国西部地区地震烈度图多呈椭圆形(杨彦明等,2017),故本研究采用椭圆模型进行烈度衰减关系拟合,公式如下
| $ I=A+B M-C_{1} \operatorname{Ln}\left(R_{\mathrm{a}}+R_{\mathrm{a} 0}\right)-C_{2} \operatorname{Ln}\left(R_{\mathrm{b}}+R_{\mathrm{b} 0}\right)-D_{1} R_{\mathrm{a}}-D_{2} R_{\mathrm{b}}+\varepsilon $ | (1) |
式中:I为地震烈度;R表示震中距;M为地震震级;R0为近场饱和因子;参数A、B、C1、C2、D1、D2为回归常数,其中C1和C2表示几何扩散阻尼的影响,D1和D2表示介质阻尼的影响;ε为回归分析中表示不确定的随机变量,通常假定为正态分布,其均值为零。
1.4 Levenberg-Marquardt法应用非线性回归理论,任何反演问题可以如下形式表达。
| $ G(m)=d $ | (2) |
式中,m代表模型参数,d代表观测数据,G为构造算子,由向量m和d构造而得。反演问题可以表述为给定观测数据d,通过最优算法寻找模型参数值m。文中采用Levenberg-Marquardt非线性反演方法(简称LM方法),寻找加权残值范数f (m)最小时模型参数值A、B、C1、Ra0、C2、Rb0,公式如下
| $ f(m)=\sum\limits_{i=1}^{m} \frac{G(m)_{i}-d_{i}^{2}}{\sigma_{i}} $ | (3) |
定义标量值函数(sclar-valued functions)为
| $ f_{i}(m)=\frac{G(m)_{i}-d_{i}}{\sigma_{i}} \quad i=1,2, \ldots, m $ | (4) |
定义向量值函数(vector-valued function)为
| $ f(m)=\begin{array}{c} f_{1}(m) \\ \vdots \\ f_{m}(m) \end{array} $ | (5) |
通过下式计算梯度值,即
| $ \nabla f(m)=2 J(m)^{\mathrm{T}} F(m) $ | (6) |
LM方法是一种迭代算法,根据式(6)计算Δm的值,并按照下式对模型参数进行更新,进入下一次迭代过程。
| $ J\left(m^{k}\right)^{\mathrm{T}} J\left(m^{k}+\lambda I\right) \Delta m=J\left(m^{k}\right)^{\mathrm{T}} F\left(m^{k}\right) $ | (7) |
式中,I为单位矩阵,J(m)代表雅克比(Jacobian)行列式,定义为
| $ J(m)=\begin{array}{ccc} \frac{\partial f_{1}(m)}{\partial m_{1}} & \cdots & \frac{\partial f_{1}(m)}{\partial m_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}(m)}{\partial m_{1}} & \cdots & \frac{\partial f_{m}(m)}{\partial m_{n}} \end{array} $ | (8) |
| $ m^{k}=m^{k}+\Delta m $ | (9) |
当满足下式时,模型参数收敛,即加权值范数为最小,此时模型参数即为所求结果。
| $ \nabla f(m)=0 $ | (10) |
根据式(1)和(3),得到本研究烈度衰减模型的标量值函数,有
| $ f_{i}(m)=\frac{A+B M-C_{1} \operatorname{Ln}\left(R_{\mathrm{a}i}+R_{\mathrm{a} 0}\right)-C_{2} \operatorname{Ln}\left(R_{\mathrm{b} i}+R_{\mathrm{b} 0}\right)-I_{i}}{\sigma_{i}} \quad i=1,2, \cdots, n $ | (11) |
根据式(8),得到雅克比行列式,公式如下
| $ J(m)=\begin{array}{cccccc} \frac{1}{\sigma_{1}} & \frac{M}{\sigma_{1}} & \frac{\operatorname{Ln}\left(R_{\mathrm{a1}}+R_{\mathrm{a0}}\right)}{\sigma_{1}} & \frac{C_{1}}{\sigma_{1}\left(R_{\mathrm{a} 1}+R_{\mathrm{a} 0}\right)} & \frac{\operatorname{Ln}\left(R_{\mathrm{b} 1}+R_{\mathrm{b} 0}\right)}{\sigma_{1}} & \frac{C_{2}}{\sigma_{1}\left(R_{\mathrm{b} 1}+R_{\mathrm{b} 0}\right)} \\ \frac{1}{\sigma_{2}} & \frac{M}{\sigma_{2}} & \frac{\operatorname{Ln}\left(R_{\mathrm{a} 2}+R_{\mathrm{a} 0}\right)}{\sigma_{2}} & \frac{C_{1}}{\sigma_{1}\left(R_{\mathrm{a} 1}+R_{\mathrm{a} 0}\right)} & \frac{\operatorname{Ln}\left(R_{\mathrm{b} 2}+R_{\mathrm{b} 0}\right)}{\sigma_{2}} & \frac{C_{2}}{\sigma_{2}\left(R_{\mathrm{b} 2}+R_{\mathrm{b0}}\right)} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ \frac{1}{\sigma_{n}} & \frac{M}{\sigma_{n}} & \frac{\operatorname{Ln}\left(R_{\mathrm{a} n}+R_{\mathrm{a} 0}\right)}{\sigma_{n}} & \frac{C_{1}}{\sigma_{n}\left(R_{\mathrm{a}n}+R_{\mathrm{a} 0}\right)} & \frac{\operatorname{Ln}\left(R_{\mathrm{b}n}+R_{\mathrm{b} 0}\right)}{\sigma_{n}} & \frac{C_{2}}{\sigma_{n}\left(R_{\mathrm{b} n}+R_{\mathrm{b} 0}\right)} \end{array} $ | (12) |
将式(5)、(11)、(12)带入式(7),得出Δm,进入迭代过程,直至满足条件式(10)时的m值,即为所求模型参数值,进而得出烈度衰减关系式。
当Rb = 0时,代入式(1),得到沿长轴方向的地震烈度椭圆衰减关系,即
| $ I_{\mathrm{a}}=A+B M-C_{1} \operatorname{Ln}\left(R_{\mathrm{a}}+R_{\mathrm{a} 0}\right)+\varepsilon $ | (13) |
当Ra = 0时,代入式(1),得到沿短轴方向的地震烈度椭圆衰减关系,即
| $ I_{\mathrm{b}}=A+B M-C_{2} \operatorname{Ln}\left(R_{\mathrm{b}}+R_{\mathrm{b} 0}\right)+\varepsilon $ | (14) |
基于已选震例和中国大陆分区原则,应用LM迭代算法进行线性回归,得到各分区地震烈度衰减关系模型,回归系数结果见表 2。
| 表 2 中国大陆地区各分区地震烈度衰减系数 Table 2 Regional attenuation coefficients of seismic intensity in Chinese mainland |
我国大陆地区幅员辽阔,历史地震烈度资料丰富,相关地震烈度衰减关系研究成果较多,如:①西部地区:汪素云等(2000)采用椭圆长、短轴联合衰减模型,选用云川藏、甘青宁、新疆发生的190个震例,统计得出中国西部地区烈度衰减关系;在此基础上,肖亮等(2015)选取新疆和川藏2个统计单元区247次震例烈度等震线资料,重新拟合西部地区地震烈度衰减关系;②东部地区:汪素云等(2000)采用椭圆长、短轴联合衰减模型,统计得出中国东部地区烈度衰减关系;崔鑫等(2010)利用华南地区20世纪48次中强地震事件96条等震线数据,拟合得到该区地震烈度衰减关系;王继等(2010)收集华中、华南地区1991-2006年25次中强地震烈度分布图,配合l9l8-l989年9次地震烈度分布图,拟合得到两区地震烈度衰减关系。以上文献所得烈度衰减系数见表 3。
| 表 3 我国大陆地区已有文献中地震烈度衰减系数 Table 3 Attenuation coefficients of seismic intensity in Chinese mainland from previous researches |
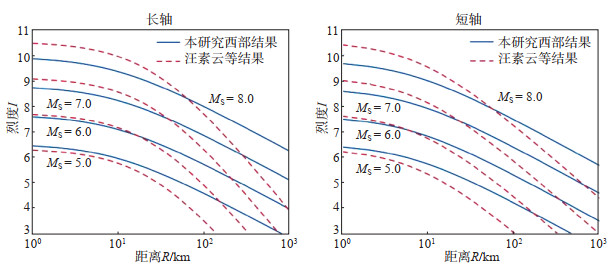
重新整理1900年以来,MS≥4.0震例的烈度等震线资料,在前人研究基础上,增加2010年以来各研究区发生的显著有感和破坏性地震,采用线性最小二乘法进行回归拟合,得到我国大陆西部、东部地区及其细分地区的地震烈度衰减关系,并与汪素云等(2000)的研究结果进行对比,结果见图 1-图 6。
|
图 1 西部地区不同文献中烈度衰减关系对比 Fig.1 Comparison of intensity attenuation relations in western China from different studies |
|
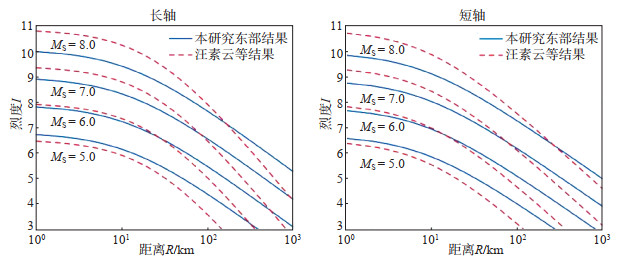
图 2 东部地区不同文献中烈度衰减关系对比 Fig.2 Comparison of intensity attenuation relations in eastern China from different studies |
|
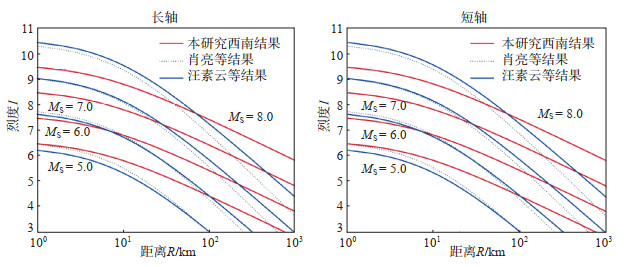
图 3 我国西南地区不同文献中地震烈度衰减关系对比 Fig.3 Comparison of seismic intensity attenuation relationships in Southwest China from different studies |
|
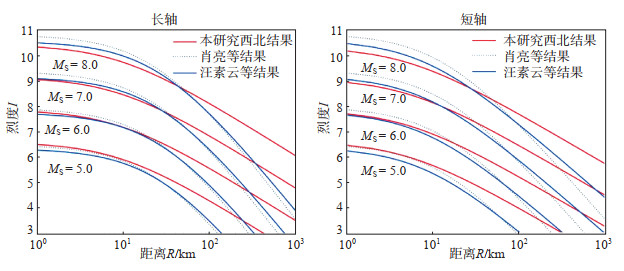
图 4 我国西北地区不同文献中地震烈度衰减关系对比 Fig.4 Comparison of seismic intensity attenuation relationships in Northwest China from different studies |
|
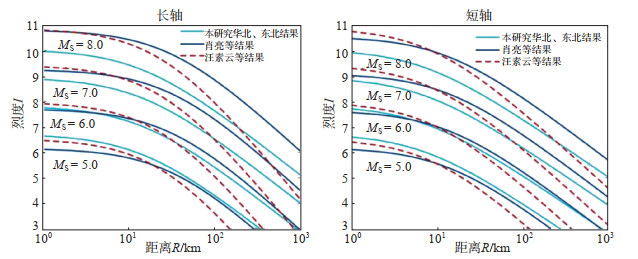
图 5 我国华北、东北地区不同文献中地震烈度衰减关系对比 Fig.5 Comparison of seismic intensity attenuation relationships in North China and Northeast China from different studies |
|
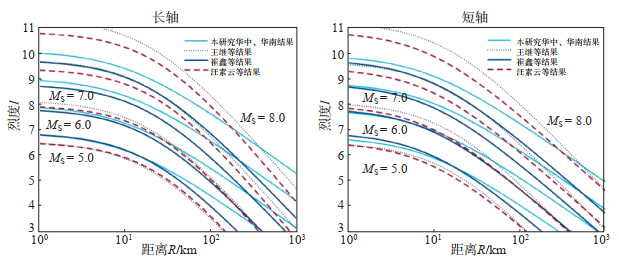
图 6 我国华中、华南地区不同文献中地震烈度衰减关系对比 Fig.6 Comparison of seismic intensity attenuation relationships in Central China and South China from different studies |
采用式(2)、(3),计算得到我国大陆西部、东部地区地震烈度衰减关系,并与汪素云等(2000)的研究结果进行对比,见图 1、图 2,可见大陆东西部地区地震烈度衰减关系趋势一致。
与汪素云等(2000)的研究结果相比,地震烈度衰减关系具有以下特点:①在近场半径R<50 km范围内:当MS震级为5.0、6.0时,两研究结果相近,当震级MS≥7.0时,本研究结果偏小;②在中远场R≥50 km范围内,本研究结果衰减更慢。
究其原因可能是:①二者参与研究的震例样本地震强度组成不同,本研究中MS≤4.0震例样本比例较高,而在汪素云等(2000)的研究中,MS≥5.0震例样本比例存在较高;②在实际工作中,对于震级5.0以下的较小地震,低烈度区现场评估烈度值存在过大倾向;③在我国大陆东部地区地震烈度衰减关系分析中,本研究使用了少量海域地震资料。
2.2.2 西部分区地震烈度回归分析采用式(2)、(3),计算我国大陆西南和西北地区的地震烈度衰减关系,并与汪素云等(2000)、肖亮等(2015)的研究结果进行对比,结果见图 3、图 4,可见不同文献中地震烈度衰减关系具有相似性。
与汪素云等(2000)、肖亮等(2015)研究结果相比,在我国西南地区和西北地区,地震烈度衰减关系具有以下特点:①在R<50 km近场范围内,当震级MS ≥ 6.0时,本文的拟合曲线略低于肖亮等(2015)和汪素云等(2000)研究者的拟合曲线,在烈度值上,沿长、短轴方向烈度估计值与两者相差0.1-0.5度左右。当震级MS = 5.0时,本研究拟合曲线和肖亮等(2015)和汪素云等(2000)研究者的拟合曲线一致;②在R>100 km远场范围内,本文的拟合曲线高于肖亮等(2015)和汪素云等(2000)研究者的拟合曲线,但长、短轴的“拟合曲线”比其他条曲线整体衰减缓慢。
在西南地区和西北2个区域内,造成本研究与肖亮等(2015)和汪素云等(2000)研究结果有所不同的原因可能是:①研究区域划分范围:本研究与肖亮等(2015)和汪素云等(2000)稍有不同;②震例样本:在回归分析中,肖亮等(2015)和汪素云等(2000)选取MS≤5.0震例样本较少,而在西南地区和西北地区的地震烈度衰减关系研究中,本研究MS≤5.0震例样本占比较高;③烈度估值:在实际工作中,对于震级5.0以下的较小地震,低烈度区现场评估烈度值结果往往有过大倾向。
2.2.3 东部分区地震烈度回归分析采用式(2)、(3),计算我国大陆华北、东北地区和和华中、华南地区的地震烈度衰减关系,并与崔鑫(2010)、汪素云等(2000)和王继等(2010)的研究结果进行对比,结果见图 5-图 6,可见不同文献中地震烈度衰减关系具有相似性。
(1)华北、东北地区。由图 5可见,地震烈度衰减关系具有以下特点:①在R<10 km近场范围内,当震级MS = 5.0时,本研究的拟合曲线略高于崔鑫(2010)和汪素云等(2000)研究者的拟合曲线,沿长、短轴方向烈度估计值与其他二者相差0.3度左右。当震级MS ≥ 7.0时,本研究的拟合曲线要略低于崔鑫(2010)和汪素云等(2000)研究者的拟合曲线;②在远场,本研究的拟合曲线在崔鑫(2010)和汪素云等(2000)研究者的拟合曲线之间。在统计回归中,本研究选用震例为震级MS ≥4.0,长、短轴拟合曲线比崔鑫(2010)和汪素云等(2000)的拟合曲线整体衰减缓慢。
(2)华中、华南地区。由图 6可见,地震烈度衰减关系具有以下特点:①在R<10 km近场范围内,当MS≤7.0时,本研究拟合曲线的斜率,从MS = 5.0到MS = 8.0,具有从大到小的变化过程;②在远场,与王继等(2010)、崔鑫(2010)和汪素云等(2000)的拟合曲线相对比可知,本研究拟合曲线较高,且长、短轴拟合曲线衰减缓慢。
在华北、东北和华南、华中2个区域内,造成本研究与王继等(2010)、崔鑫(2010)和汪素云等(2000)研究者结果有所不同的原因可能是:①研究区域划分范围:本研究与王继等(2010)、崔鑫(2010)和汪素云等(2000)研究者稍有不同;②震例样本:在回归分析中,肖亮等(2015)和汪素云等(2000)选取MS≤5.0震例样本较少,而在华北、东北地区和华南、华中地区的地震烈度衰减关系研究中,本研究MS≤5.0震例样本占比较高;此外,在华中、华南地区,本研究使用了少量海域地震资料;③烈度估值:在实际工作中,对于震级5.0以下的较小地震,低烈度区现场评估烈度值结果往往有过大倾向。
3 灾情评估根据上述分析,得出我国根据各分区地震烈度衰减关系,公式如下。
(1)西南地区烈度衰减关系,即
| $ I_{\mathrm{a}}=2.7295+1.00372 M-0.67429 \operatorname{Ln}\left(R_{\mathrm{a}}+6.7391\right) $ | (15) |
| $ I_{\mathrm{b}}=2.7493+0.99204 M-0.70817 \operatorname{Ln}\left(R_{\mathrm{b}}+4.8988\right) $ | (16) |
(2)西北地区烈度衰减关系,即
| $ I_{\mathrm{a}}=2.24+1.2685 M-0.91526 \operatorname{Ln}\left(R_{\mathrm{a}}+8.6547\right) $ | (17) |
| $ I_{\mathrm{b}}=1.8026+1.227 M-0.8572 \operatorname{Ln}\left(R_{\mathrm{b}}+0.7677\right) $ | (18) |
(3)西部地区烈度衰减关系,即
| $ I_{\mathrm{a}}=2.5766+1.1372 M-0.7854 \operatorname{Ln}\left(R_{\mathrm{a}}+9.0078\right) $ | (18) |
| $ I_{\mathrm{b}}=2.4734+1.0899 M-0.80135 \operatorname{Ln}\left(R_{\mathrm{b}}+5.7984\right) $ | (19) |
(4)我国华北、东北地区的烈度衰减关系,即
| $ I_{\mathrm{a}}=4.2068+1.1089 M-1.1527 \operatorname{Ln}\left(R_{\mathrm{a}}+13.7867\right) $ | (20) |
| $ I_{\mathrm{b}}=3.1247+1.1048 M-1.0033 \operatorname{Ln}\left(R_{\mathrm{b}}+6.7178\right) $ | (21) |
(5)我国华中、华南地区的烈度衰减关系,即
| $ I_{\mathrm{a}} =4.0229+1.0734 M-1.0594 \operatorname{Ln}\left(R_{\mathrm{a}}+10.4091\right) $ | (22) |
| $ I_{\mathrm{b}} =3.5078+1.0716 M-1.0334 \operatorname{Ln}\left(R_{\mathrm{b}}+7.9512\right) $ | (23) |
(6)东部地区的烈度衰减关系,即
| $ I_{\mathrm{a}} =4.0404+1.0870 M-1.0809 \operatorname{Ln}\left(R_{\mathrm{a}}+11.8607\right) $ | (24) |
| $ I_{\mathrm{b}} =3.3340+1.0897 M-1.0223 \operatorname{Ln}\left(R_{\mathrm{b}}+7.4965\right) $ | (25) |
选取1990-2007年23次MS≥6.0地震事件及2008年以来88次MS≥5.0地震事件,以实际震害面积与烈度衰减经验统计模型所得面积之比为指标,验证模型与实际震害的吻合程度,结果见表 4。地震烈度10度、11度区震害资料有限,未在表 4列出。因涉及震例较多,表 4仅给出部分典型震例结果。
| 表 4 统计地震的实际震害面积与模型面积之比 Table 4 Statistics of the ratio of actual earthquake-damaged area to model area |
对于不同烈度区实际震害与模型面积比结果,由表 4可见:9度区面积比最大值为40.00%,最小值为6.07%,中位值为7.25%,剔除奇异点后平均值为6.62%;8度区面积比最大值为52.31%,最小值为0.39%,中位值为3.00%,剔除奇异点后平均值为3.70%;7度区面积比最大值为70.00%,最小值为0.09%,中位值为1.15%,剔除奇异点后平均值为1.75%;6度区面积比最大值为24.10%,最小值为0.01%,中位值为1.28%,剔除奇异点后平均值为2.22%。
通过以上数据对比发现,震害面积比最大值与最小值的比值可达数百倍以上,说明地震作用的离散性大,但中位值与平均值的变化趋势基本一致,说明利用地震烈度衰减关系评估震害面积有一定规律可循,具体体现在:与模型面积相比,高烈度区实际震害面积往往偏大,而低烈度区实际震害面积往往偏小。究其原因是可能是:①在椭圆烈度衰减关系模型中,烈度随震中距呈对数关系衰减,而实际烈度衰减关系受震源特性、深部构造、传播介质、场地条件、建筑物结构类型和居民点分布、地形等因素的影响;②采用LM算法进行回归分析,等震线仅由式(1)中的6个系数确定,忽略了各影响因素彼此之间的耦合作用,故造成本研究结果与真实烈度数据有所偏差。
4 结果与建议收集整理1900-2019年,我国大陆西部地区488个地震和东部地区182个地震的烈度等震线资料,采用长、短轴椭圆模型,应用LM算法,拟合得到东、西部地区及各分区地震烈度衰减关系。将研究结果应用到:1990-2007年MS≥6.0地震震例和2008-2019年MS≥5.0地震事件的烈度评估计算,以实际震害面积与烈度衰减经验统计模型所得面积之比为指标,验证模型与实际震害的吻合程度,结果发现:利用本研究所得地震烈度衰减关系,对实际震害面积进行预判和评估时,与模型面积相比,高烈度区实际震害面积往往偏大,而低烈度区实际震害面积往往偏小。
建议按照本研究所得烈度衰减关系估计实际震害面积时,将8度区模型面积放大约1.5-2.0倍,7度区模型面积缩小约1.5-1.6倍,6度区模型面积缩小约1.8-2.0倍。
在进行烈度分布评估工作时,为了避免烈度衰减关系标定的等震线彼此之间产生耦合作用,可以分别统计不同震级下各烈度圈的长、短轴半径,与烈度衰减关系模型相结合进行判断。
陈达生, 刘汉兴. 地震烈度椭圆衰减关系[J]. 华北地震科学, 1989, 22(3): 77-82. |
崔鑫, 苗庆杰, 王金萍, 等. 华北地区地震烈度衰减模型的建立[J]. 华北地震科学, 2010, 28(2): 18-21. DOI:10.3969/j.issn.1003-1375.2010.02.004 |
国家地震局. 中国地震烈度区划图(1990)概论[M]. 北京: 地震出版社, 1996.
|
帅向华, 姜立新, 王栋梁. 国家地震应急指挥软件系统研究[J]. 自然灾害学报, 2009, 18(3): 99-103. DOI:10.3969/j.issn.1004-4574.2009.03.017 |
汪素云, 俞言祥, 高阿甲, 等. 中国分区地震动衰减关系的确定[J]. 中国地震, 2000, 16(2): 99-106. DOI:10.3969/j.issn.1001-4683.2000.02.001 |
王继, 俞言祥. 华中、华南中强地震区地震烈度衰减关系研究[J]. 震灾防御技术, 2008, 3(1): 20-26. DOI:10.3969/j.issn.1673-5722.2008.01.003 |
肖亮, 俞言祥. 中国西部地区地震烈度衰减关系[J]. 震害防御技术, 2015, 6(4): 358-371. |
许卫晓, 孙景江, 杨松伟, 等. 应用烈度衰减关系进行烈度分布快速评估的偏差特性研究[J]. 世界地震工程, 2012, 28(4): 100-104. |
杨天青, 姜立新, 杨桂岭. 地震人员伤亡快速评估[J]. 地震地磁观测与研究, 2006, 27(4): 39-43. |
杨彦明, 姜立新, 王祯祥. 基于Levenberg-Marquardt方法的内蒙古及邻区地震烈度影响场改进技术[J]. 地震, 2017, 37(3): 117-126. |
中国地震局震害防御司. 中国近代地震目录(公元1912-1990年)[M]. 北京: 地震出版社, 1999.
|
中国地震局震监测预报司. 1996-2000年中国大陆地震灾害损失评估汇编[M]. 北京: 地震出版社, 2001.
|
中国地震局震灾应急救援司. 1966-1989年中国大陆地震灾害损失评估汇编[M]. 北京: 地震出版社, 2015.
|
中国地震局震灾应急救援司. 2001-2005年中国大陆地震灾害损失评估汇编[M]. 北京: 地震出版社, 2010.
|
中国地震局震灾应急救援司. 2006-2010年中国大陆地震灾害损失评估汇编[M]. 北京: 地震出版社, 2015.
|
 2021, Vol. 42
2021, Vol. 42

