2. 中国北京 100029 中国地震局地质研究所地震动力学国家重点实验室
2. State Key Laboratory of Earthquake Dynamics, Institute of Geology, China Earthquake Administration, Beijing 100029, China
地震孕育过程中产生的地壳变形和震源介质变化在地表会引起重力变化,通过开展连续重力观测或定期相对重力复测,有可能捕捉到地震的这些前兆信息。重力场具有明确的地球物理含义,属于构造运动的一种表现形式,一般分为“静态”重力场和“动态”重力场。“静态”重力场是指,基于地球重力模型或实测重力数据,获取布格重力及均衡重力异常信息,用来研究地质构造特征、地壳物性密度变化及地壳均衡状态等地质时间尺度的地学问题(陈石等, 2011a, 2011b, 2014);“动态”重力场是指,在年时间尺度内,利用流动作业方式获取的重力异常变化信息,主要用来认识强震孕育机理、捕捉地震前兆信息和判定地震危险区(祝意青等, 2009, 2017, 2020;申重阳等2010,2011;陈石等,2015;Chen et al,2016a)。
当前主要基于“场”模式开展地震监测预测,而应用地表观测的重力场变化信息来开展异常源的研究,即“以场求源”问题的研究仍不够深入。众所周知,地表观测的重力场变化是测量误差、地表水影响、测点三维形变、地下介质密度变化及物质迁移等信息的综合反映(陈运泰等,1980;陈石等,2011c)。准确分离并识别这些因素对重力场变化信息的影响,是比较困难的事情,原因如下:①深部介质变化的先验信息及参数难以观测或获取;②现有重力仪器观测精度偏低,信噪比不高。此外,在重力场变化的相关研究中,经常采用大地测量学方法进行数据计算和解释,间接造成了上述困难无法克服。为此,尝试将三维欧拉反褶积方法引入重力场变化分析。该方法是Reid等(1990)结合Thompson(1982)在欧拉齐次方程的研究基础上建立起来的,其最大优势是,在先验信息缺乏情况下,仍能较好完成位场数据反演与解释工作(范美宁,2006)。
文中对鄂尔多斯南缘地区EGM2008重力场模型数据及2014—2017年相对重力观测数据进行精细化处理。在此基础上,以布格重力异常、1年尺度差分重力场和3年尺度累积重力场为研究对象,分析上述重力场异常变化的场源特征。设计一个与实际重力观测相似的理论模型模拟地表重力场变化,同时利用三维欧拉反褶积方法对场源参数进行反演,优选与模型接近的构造指数及滑动窗口大小等参数,对相对重力观测网数据进行欧拉反演,并利用水平梯度滤波法对发散的反演结果进行优化,结合地震目录资料,对获取的三维场源信息进行分析与解释。
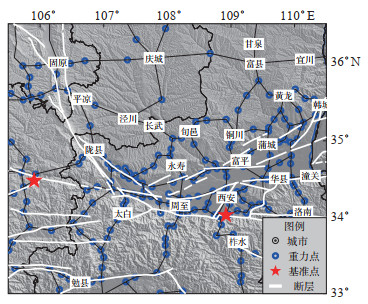
1 测区概况与数据处理鄂尔多斯南缘地区位于我国青藏块体与华北块体交汇区域,地质构造形式多样,动力学环境复杂。同时,该地区位于我国重要的汾渭地震带和南北地震带北段,历史上曾发生多次6级以上大震,属于我国地震活动重点监视区。该区发育多条活动断裂,其中鄂尔多斯南缘断裂、渭河断裂及秦岭北缘断裂控制着该区主要构造变形演化格局,区内其他断裂进一步把鄂尔多斯南缘地区分隔为不同样式的地质构造单元,单条或多条断裂边界或交汇处成为地震孕育的主要场所。为了监测鄂尔多斯南缘地区地震活动潜在危险性,尤其是渭河断陷盆地内主要断裂的地球物理场异常变化,陕西省地震局于20世纪80年代建立了相对重力观测网,每年观测1期。2008年汶川8.0级地震后,依托“震后恢复重建”等项目,对原有相对重力观测网进行优化改造,改造后的重力测网覆盖陕西全境,加上“陆态网络”一、二期建立的重力站点,重力站点总计达200余座,点间距基本在20—30 km,站点分布见图 1。这些重力站点覆盖渭河盆地及邻区大部分断裂,且分布相对合理,为监测断裂活动引起的重力变化奠定了坚实的基础(曹建平等,2014;张永奇等,2014)。
|
图 1 鄂尔多斯南缘地区重力点及断裂分布 Fig.1 Distribution of gravity points and faults in the southern margin of the Ordos |
基于重力资料开展鄂尔多斯南缘地区的研究,以往集中在数据精细化处理、重力场变化及重力网的映震能力分析等方面,针对深部场源特征的研究相对较少。因此,尝试基于EGM2008重力场模型数据及相对重力数据,利用欧拉反褶积方法,对该区进行场源特征反演。反演前将相对重力观测数据进行平差计算,具体流程为:①采用中国地震局实用化攻关推广软件——LGADJ,对多期重力观测资料进行独立平差计算,解算重力仪一次项周期误差等参数的区域适定解,计算各台仪器观测精度,合理确定其先验方差;②以四川广元、西安子午、甘肃天水等绝对测点为起算基准,采用经典平差方法进行平差计算,对其中因周围环境改变而出现异常的个别测点进行改正或删除;③采用克里金插值算法拟合离散重力场,获得不同时间尺度的重力场。
2 方法原理欧拉反褶积方法不依赖场源密度参数,仅与场源位置的几何参数相关,使得反演问题得以简化(Reid et al,1990)。通过求解欧拉方程,可以确定场源位置的三维空间位置,并可对不同类型地质体给出参数估计,公式如下
| $ \left({x - {x_0}} \right)\frac{{\partial T}}{{\partial x}} + \left({y - {y_0}} \right)\frac{{\partial T}}{{\partial y}} + \left({z - {z_0}} \right)\frac{{\partial T}}{{\partial z}} = N\left({B - T} \right) $ | (1) |
式中,(x,y,z)为观测点的位置,(x0,y0,z0)为场源位置,T为位场异常,
构造指数N反映了位场异常强度随场源深度变化的衰减率,一般与场源几何结构有关。N的选取是场源位置确定的关键。根据不同构造特征,针对重力场异常数据,N的范围一般取0—2较为合适,其中断层、岩脉、台阶等构造指数皆不同(范美宁,2006;高倩等,2015;刘芳等,2016;翟丽娜等,2020)。三维重力欧拉反褶积方法的反演流程如下:①对实测离散重力位场数据进行网格化;②计算重力位场异常在x、y、z三个方向的导数;③选择适当的构造指数N及窗口大小。根据异常体性质选择构造指数N,窗口大小根据异常体大小进行选择,一般应覆盖异常范围,不得低于3倍测点间距。根据精度要求确定允许误差;④解方程组,求出场源位置参数及背景值;⑤根据解的汇聚位置、深度调整参数。如果对反演结果满意,结束计算,否则重新选择参数重复步骤②、③,直至对结果满意为止(高倩等,2015;刘芳等,2016;翟丽娜等,2020)。
3 模型反演欧拉反褶积方法不需要已知场源先验信息,即可对场源参数进行反演与解释。反演计算时,应选择合适的构造指数N,并求出异常在x、y、z三个方向的导数,即可组成线性方程组进行求解(范美宁,2006)。在实际应用中,地质情况复杂,场源形态也不确定,所以如何选择构造指数,需要对不同模型进行反复计算来确定(鲁宝亮等,2009)。此外,滑动窗口大小的选取,一般需考虑测点间距、异常形态特征等,在一个窗口内应有足够多的测点满足方程组的求解,并要覆盖一个场源异常形态。对于反演结果的评价,需要通过求得场源位置参数的水平误差和垂直误差大小,及反演场源位置解的三维空间聚集程度和与地质认识是否符合等判断,即场源位置越集中,其精度及收敛性越好,反之解的收敛性差(高倩等,2015;刘芳等,2016)。
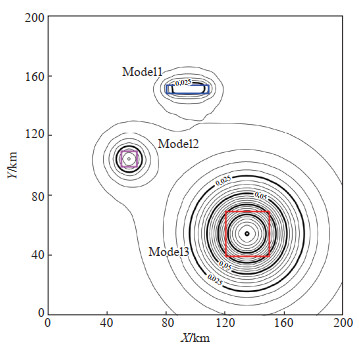
基于对欧拉反褶积法的认识,根据鄂尔多斯地块南缘地区现有重力观测网形态及规模,设计一个相对符合实际观测情况的理论模型。以3个直面正六面体组合模型为研究模型,假设其分别位于上地壳、中地壳和下地壳。其中模型1(Model1)位于上地壳,单元尺寸为20 km×20 km×20 km,中心埋深为5.5 km;模型2(Model2)位于中地壳,单元尺寸为10 km×10 km×10 km,中心埋深为11.5 km;模型3(Model3)位于下地壳,单元尺寸为30 km×30 km×30 km,中心埋深为22.5 km。3个模型密度变化统一取为3.0 g·cm-3,正演计算模型在地表重力测网的理论异常值,用于模拟观测的重力变化信号和优选反演参数,模型异常见图 2,矩形框表示场源模型在地表的水平投影。地表重力测网点间距设计为5 km,测网长度在X、Y方向均为200 km、深度方向为50 km,3个不同深度的场源模型参数见表 1,可见3个模型的尺度特征不同,埋深也不同,正演结果显示理论异常范围在(0—120)×10-8 m·s-2。
|
图 2 不同深度场源组合模型及正演异常 Fig.2 Combination models of different depth field sources and forward modeling anomalies |
| 表 1 理论场源模型参数 Table 1 The theoretical field source model parameters |
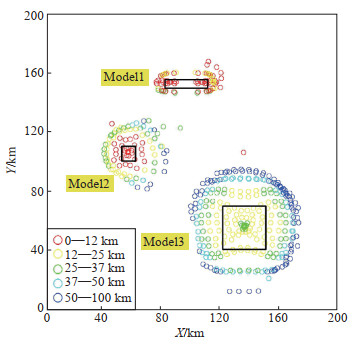
基于上述理论测试结果,实际测试时设计多个参数组合,其中构造指数分别选择0.5、1、1.5、2,滑动窗口分别选择4—8倍的测点距离。通过对多次试验结果进行对比分析,认为选择构造指数N = 1,滑动窗口大小在4个测点距离时,反演结果的聚集程度更符合模型的几何结构,组合模型的反演深度误差范围限制在10%以内。图 3给出计算所得一组最佳反演结果,图中彩色圆圈为反演的场源参数,共获得467组解,黑色矩形框为理论组合模型位置,可见聚集程度相对较好,场源特征明显。其中模型2(Model2)和模型3(Model3)反演结果最好,模型1(Model1)反演结果稍差。
|
图 3 基于欧拉反褶积的反演结果空间分布 Fig.3 Spatial distribution of inversion results based on Euler deconvolution |
欧拉反演的基本条件是模型满足欧拉齐次方程的假设条件,此时反演结果应该是准确的。然而实际上地质体的位置和构成情况复杂,无法用任何一种模型准确表达,这就会导致反演解出现发散现象(姚长利等,2004;管志宁等,2005;石磊等,2008),因此需要寻找一种减弱或消除反演解发散的方法,研究表明水平梯度滤波法是一种比较有效的方法。在利用欧拉反褶积方法开展反演研究时,当窗口滑动到异常体边缘时,梯度值变小甚至趋近于零,此时反演容易出现发散解。理论上,水平梯度决定了场源的水平位置,构造指数决定了场源的深度,因此构造指数越大,反演的深度越深,结果将更加发散(姚长利等,2004;郑秋月等,2021),使用水平梯度滤波法即可克服上述问题。
设
水平梯度滤波法优势在于:①可剔除水平梯度较小的区域网格点,选择水平梯度模相对较大的区域参与反演;②可去除因测网不均匀插值带来的虚假网格点信息(姚长利等,2004;管志宁等,2005;郑秋月等,2021)。文中在计算场源位置时,采用水平梯度滤波法,对传统的欧拉反演结果予以优化,其中k值取为1。
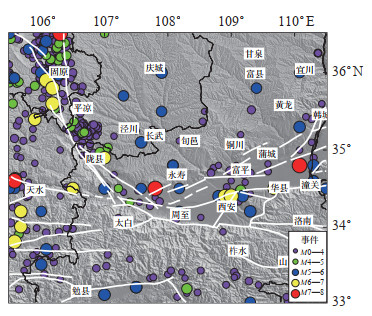
5 重力场变化及场源特征反演与解释 5.1 鄂尔多斯南缘地区“静态”重力场变化特征地震孕育发生是区域构造应力积累与释放的过程,震源位置和震源机制是岩石圈动力学过程的反映,通过地震可以了解地下深部的地质构造和应力状态,同时可为分析重力异常变化与地震分布的关系提供便利。为此,统计鄂尔多斯南缘地区历史地震目录,绘制历史地震分布图,见图 4。
|
图 4 鄂尔多斯南缘地区地震分布 Fig.4 Earthquake distribution in the southern margin of the Ordos area |
重力位场异常可以表征地质构造运动过程,常用于划分构造单元、识别断裂形态和盆地边界(马宗晋等,2006)。一般认为,自由空气重力异常可以表征地下物质盈亏程度;布格重力异常可以反映深部构造特征,被称为构造运动的“活化石”(陈石等,2011b)。在分析鄂尔多斯南缘地区“动态”重力场变化之前,分析“静态”重力场变化特征。基于EGM2008地球重力模型,计算自由空气重力异常和布格重力异常(Sandwell et al,2009;Pavlis et al,2012),结果见图 5。
|
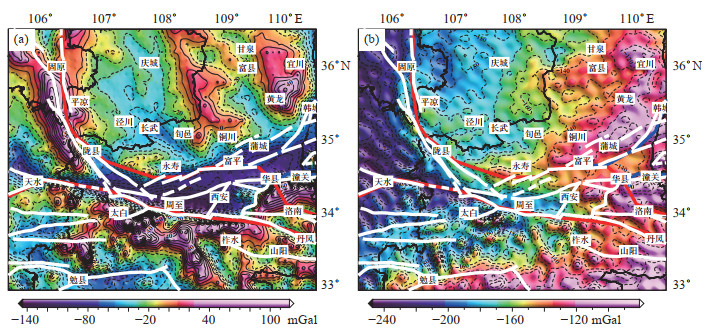
图 5 鄂尔多斯地块南缘地区重力异常 (a)自由空气异常;(b)布格重力异常 Fig.5 Gravity anomaly in the southern margin of the Ordos block |
图 5(a)为自由空气重力异常,异常范围基本在(-140—110)×10-5 m·s-2。该异常与地形具有较强的相关性,在高海拔的山地,重力异常表现为正值,在低海拔的平原和盆地,重力异常表现为负值,自由空气异常基本反映了该区构造单元的大体轮廓。图 5(b)为布格重力异常,研究区整体表现为负值异常,范围在(-240—-80)×10-5 m·s-2。研究区西北端靠近青藏高原东北缘地区,其布格重力异常呈现极小负值,向SE,重力异常呈逐渐增大趋势,异常整体形态与断裂及构造区分布具有一定对应关系。结合图 4所示的地震分布,发现大部分地震震中与断裂带发育位置具有较好的一致性,但有些地震与断裂之间的对应关系不明显。此外,重力异常的变化特征与地震分布也具有一定相关性。进一步说明,重力异常变化、断裂活动与地震孕育发生具有较好的协调性和一致性。
5.2 “静态”重力场欧拉反演与解释为了全面掌握鄂尔多斯南缘地区重力异常变化的场源特征,对该区布格重力异常进行欧拉反演计算。反演前,对布格重力异常进行坐标转换,将大地坐标转换为平面直角坐标,采用克里格插值算法进行插值,并采用高斯滤波进行平滑。在此基础上,对布格重力异常数据进行欧拉反演,策略如下:①构造指数取1.5;②X、Y方向点距均设置为10 km;③水平梯度滤波倍数k = 0.5;④滑动窗口设为4—8倍点距。由此获得基于布格重力异常的鄂尔多斯南缘地区场源特征,见图 6。从“静态场”角度分析鄂尔多斯南缘地区场源特征,由图 6可知,在4—8倍的欧拉反演结果中,场源分布的水平位置和深度基本相同,聚集性相对较好的区域集中在断裂边界带附近,尤其是研究区西部的海原—六盘山地区以及南北地震带北部地区,异常源聚集性较好且与断裂走向基本一致,呈NS向分布。渭河盆地内部场源呈EW向分布特征,主要沿断裂走向展布。在鄂尔多斯地块内部出现平凉—泾川和庆城—富县地区2个场源特征较显著区域。秦岭造山带场源集中在勉—略大断裂、月河断裂和山阳断裂附近。从场源深度看,0—30 km深度的场源占整个反演结果的90%以上,表明该区布格重力异常变化主要由浅部异常源引起。结合图 4可知,地震分布的三维位置与基于布格重力异常计算的场源位置吻合程度较高。

|
图 6 基于布格重力异常的鄂尔多斯南缘地区场源特征 Fig.6 Field source characteristics in the southern margin of Ordos based on Bouguer gravity anomaly |
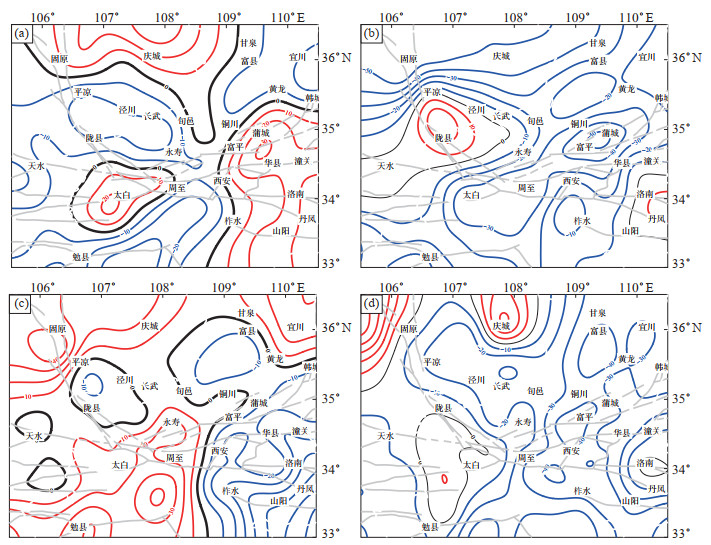
选取研究区2014—2017年相对重力数据,计算“动态”重力异常变化,结果见图 7。其中(a)—(c)图分别表示2014年8月—2015年8月、2015年8月—2016年7月、2016年7月—2017年7月的1年尺度重力差分变化结果,(d)图表示2014年8月—2017年7月3年尺度的重力累积变化结果。图中灰色线表示断裂带,蓝色等值线表示负变化,红色等值线表示正变化,黑色等值线表示“0”值线,等值线间距10×10-8 m·s-2。因部分地区重力站点分布不均,采用克里格插值算法,对平差后重力数据进行插值及高斯滤波,等值线覆盖范围与测网范围基本一致。在测点稀疏地区,重力场变化的可信度偏低,不做深入分析。
|
图 7 鄂尔多斯地块南缘地区2014—2017年重力变化(单位:10-8 m· s-2) (a) 观测时段:2014-08 — 2015-08;(b) 观测时段:2015-08 — 2016-07;(c) 观测时段:2016-07 — 2017-07;(d) 观测时段:2014-08 — 2017-07 Fig.7 Gravity changes in the southern margin of the Ordos block from 2014 to 2017 (unit: 10-8 m· s-2) |
由图 7(a)可见,2014年8月—2015年8月,该区重力变化基本以西安为界,以西大部分地区以负值变化为主,以东地区以正值变化为主。在成县—太白断裂与秦岭北缘断裂交汇处出现局部重力正值变化,量值约20×10-8 m·s-2。另一个重力正值变化区位于海原—六盘山断裂带以东固原、庆城一带,量值在30×10-8 m·s-2。以渭河断裂与长安—临潼断裂交界为中心出现不规则重力四象限分布特征,整体来看,重力场展布特征受主要断裂控制。由图 7(b)可见,2015年8月—2016年7月,研究区重力以负值变化为主,在西秦岭北缘断裂、六盘山—宝鸡断裂带附近出现重力变化梯度带,差异变化达70×10-8 m·s-2。其他地区重力场变化相对平稳,变化量基本在(-40— -10)×10-8 m·s-2。由图 7(c)可见,2016年7月—2017年7月重力场变化相对复杂。与图 6(a)相比,重力场出现反向变化,基本以西安为界,以西地区重力表现为大范围正值变化,而东部则为负值变化。在六盘山—宝鸡断裂附近不仅存在重力变化梯度带,还具有四象限分布特征。在秦岭中部及鄂尔多斯东南部地区也出现了重力变化梯度带。由图 7(d)可见,2014年8月—2017年7月,研究区重力变化相对平稳,且以负值变化为主,变化量基本在(-40— -10)×10-8 m·s-2,仅在海原—六盘山断裂以西地区出现局部正值变化,变化量最大为50×10-8 m·s-2,可见3年尺度重力累积变化不明显,未出现大震、中强震的孕育特征。
由图 7可见,1年尺度的重力场变化在某些区域存在一定继承性,但大部分地区的重力变化存在明显差异。海原—六盘山—陇县断裂带附近重力变化梯度带位置在不同时间尺度上基本一致,但是变化量存在差异,重力变化等值线的展布和断裂分布具有一定对应关系。研究表明:半年尺度,甚至1年尺度的重力变化依然存在正负波动的变化特征。这种波动可能由近地表局部影响、观测误差所导致,目前尚无法有效分离各种场源引起的重力变化。理论上,若为深部场源引起的区域重力变化,其在不同时间尺度内应具有相似性和一致性,此区域即为比较可靠的异常源位置,也是物质汇集、应力积聚区域,未来发生地震的可能性相对较大。
5.4 “动态”重力场欧拉反演结果与解释基于常规欧拉反褶积方法,对不同时间尺度的重力变化进行反演,寻找聚集性好、场源重复性好的区域。此类区域往往物质积累相对集中、构造活动频繁。实际反演时设定网格化间距为10 km,构造指数为1,窗口大小为5—8倍测点间距。反演完成后,对反演结果进行统计,发现反演解个数存在差异,具体结果见表 2。
| 表 2 改正前后基于不同滑动窗口获得的反演结果个数 Table 2 The number of inversion results obtained based on different sliding windows before and after correction |
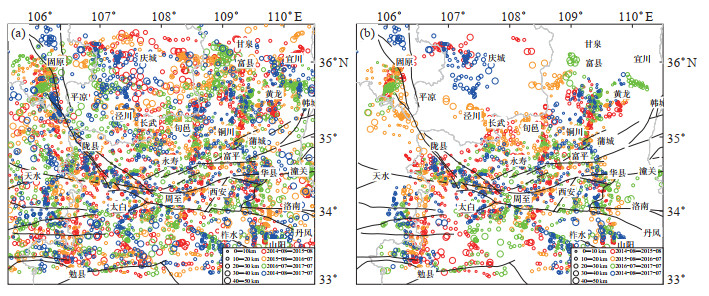
对不同反演结果进行对比分析,将6倍测点间距获得的结果作为最优解来进行分析,具体反演结果见图 8(a)。图中圆圈表示反演的场源位置,圆圈大小与场源深度相对应,采用红、黄、绿、蓝4种颜色表示2014—2017年不同时间段的反演结果。由图 7可知,从引起重力场变化的不同时间尺度结果来看,场源位置相对分散,无明显规律性。总体而言,研究区边缘地区场源深度反演结果相对较深,内部区域场源则相对较浅。在不同时间尺度下,海原—六盘山—陇县断裂带、成县—太白断裂、华山山前断裂以及韩城断裂附近地区场源位置集聚性较高,而鄂尔多斯地块南部及秦岭造山带南部场源位置相对分散。作为一种地震前异常信号,场源位置的分散型分布特征表明,鄂尔多斯南缘地区近年来不具备中强地震孕育与发生的条件,同时说明,2014—2017年重力场变化属于一种随机的、正常的波动变化,地震紧迫性相对较弱。此外,统计得到不同深度的反演解个数,具体结果见表 3。
|
图 8 鄂尔多斯南缘地区2014—2017年重力变化场源特征 (a) 常规欧拉反演结果;(b) 水平梯度滤波结果 Fig.8 Field source characteristics of gravity changes in the southern margin of Ordos from 2014 to 2017 |
| 表 3 改正前后不同深度的反演结果个数 Table 3 The number of inversion results at different depths before and after correction |
由表 3可知,2014—2017年,发生重力变化的场源深度集中在0—50 km,其中场源深度为5—30 km的反演结果约占60%。对比发现,2014年8月—2015年8月,场源深度0—10 km的反演解数量较少,深度50—100 km的反演解数量较多,说明该期重力场变化受深部物质影响较大。在该时间范围之前曾于2013年7月22日发生岷县—漳县MS 6.6地震,该地震距研究区西部仅150 km,因此重力变化可能受到地震远程应力调整及物质运移的影响。其他3期的反演结果显示,大部分场源深度在30 km以上,与该区震源深度基本吻合。
利用常规欧拉反演方法可获得比较合理的场源特征,但反演结果发散性严重,采用水平梯度滤波法对反演结果进行优化,发现欧拉反演结果更加聚集收敛,发散现象显著减弱,场源特征更加明显,具体结果见图 8(b),与图 8(a)对比可知,研究区边缘大部分区域反演结果数量明显减少。这是因为,水平梯度法删除了测点稀疏造成的不真实反演结果。总体来看,研究区西北部的海原—六盘山地区出现场源丛集现象,鄂尔多斯地块内部场源集聚性较好地区分布在庆城一带。渭河断陷盆地内部反演结果集聚性较好区域基本分布在主要断裂附近,且场源展布与断裂走向基本一致。秦岭造山带的场源特征相对分散,且场源位置相对较深。同时,统计水平梯度滤波反演结果,与常规欧拉反演结果(表 2,表 3)进行对比,可知:从5—8倍测点间距滑动窗口结果看,采用水平梯度滤波法效果较好,反演解数量较常规欧拉反演结果至少减少50%,剔除了大部分不真实的场源信息;采用水平梯度滤波法处理后,对场源深度反演结果改正效果显著,进一步表明相对重力观测结果主要反映深度在30 km以内的异常源信息。
5.5 重力变化场源特征与地震的关系鄂尔多斯南缘地区在地质构造划分上主要包含鄂尔多斯地块南部、渭河断陷盆地及秦岭造山带,在地震带划分上主要包含汾渭地震带的渭河地震带及南北地震带北部。该研究区历史上曾发生多次6级以上强震,具备强震发生的历史背景和构造条件。据历史地震记录和震源机制解结果,鄂尔多斯南缘地区震源深度相对较浅,多在30 km以内(王卫东,2009;杜建军,2016)。对图 4、图 6、图 8及表 2进行细致分析,发现基于布格重力异常数据计算的“静态”场源位置和基于相对重力观测数据计算的“动态”场源位置,均与研究区历史地震分布位置具有高度一致性,表明场源集聚性较好的地区有利于地震的孕育与发生(刘芳等,2016;郑秋月等,2021)。本研究结果表明,海原—六盘山断裂带、陇县—宝鸡断裂带、渭河断裂带西段以及华山山前断裂东段场源积聚性较好,未来发生地震的可能性较高。其他构造区异常源呈现相对性和随机性,地震危险性相对较弱。此外,据欧拉反演深度,重力场源集中在30 km以内,位于中上地壳,与王卫东(2009)、杜建军(2016)等研究所得震源深度一致。
6 结论作为我国东、西部不同构造单元的连接部位,鄂尔多斯南缘地区不仅是物质流通的重要通道,也是青藏块体和华北块体相互作用的关键部位。受2种不同构造应力的影响,该区山地隆升,盆地下陷,断裂发育,地震频发,历史上发生多次6级以上强震,甚至8级巨震。因此,鄂尔多斯南缘地区的地震危险性历来是地学研究的重点关注问题之一。近年来,随着地震观测手段的日益丰富、观测技术的不断提高,对孕震机理、发震构造、前兆信号的研究日趋成熟,并取得长足进展(陈石等, 2011c, 2014, 2015;祝意青等, 2017, 2020),如基于重力观测资料开展地震监测预测,取得丰硕成果(祝意青等,2009;申重阳等,2010;Chen et al,2016a, 2016b)。但是,大多数工作是基于重力异常“场”开展的,针对重力异常“源”开展的工作相对较少,主要原因是缺少足够的先验信息。为此,本研究尝试采用在地球物理勘探工作中应用广泛的三维反褶积方法,进行重力变化场源特征研究,取得以下认识。
(1)利用欧拉反褶积方法进行反演,关键在于选择合适的构造指数、滑动窗口大小等参数。通过构建模型,正演得到基本可以反映真实重力变化的模型参数。通过不同实验方案进行测试,发现当构造指数为1,滑动窗口为4—8倍点位间距时,反演效果最佳。
(2)反演结果表明:海原—六盘山—陇县断裂、陇县—宝鸡断裂、渭河断裂和华山山前断裂附近,在不同时间尺度下场源特征一致性较好。结合图 4,可知以上地区也是中小地震频发区域,即更易于应力积累、能量积聚而发生地震的位置。由图 8、表 3可知,场源反演深度集中在5—30 km范围内,属中上地壳。据地震震源机制解,可知该深度范围也是鄂尔多斯南缘地区的主要震源深度。
(3)欧拉反褶积方法适用于反演重力场变化异常的场源信息,不同的场源位置及深度揭示了不同的构造信息,多期重力变化反演三维场源特征一致性较好,表明该区存在物质积聚和应力增强;反之,则该区地震危险性较弱。图 8(a)显示,在不同时间尺度下,场源位置相对分散,表明大部分地区的重力变化是随机的物质运动现象,属于较短期的地壳活动现象或者与观测误差不确定性有关。但图 8(b)显示,经水平梯度滤波的欧拉反演结果聚集性和收敛性更强,场源特征更加明显。因此,在实际反演时,需要对欧拉反演结果做进一步滤波处理。
需要说明的是,选择2014—2017年相对重力观测数据开展研究,主要是因为,2013年陕西重力测网进行了优化改造,增建大量站点,而2018年进行了二次优化改造,删减了大量站点。因此,陕西重力测网在该时间范围内点位密度相对较高,分布较均匀。此外,本研究在建立正演模型时,仅考虑了直立六面体组合,实际地质构造更复杂,而文中测试模型相对简单。尽管如此,本研究结果仍能验证欧拉反褶积方法的可靠性和适用性。希望通过本研究,为鄂尔多斯南缘地区地震危险性研判提供一种新的研究思路和技术途径。
文中流动重力数据由国家重力台网中心提供,撰写过程中多次与云南省地震局郑秋月工程师进行讨论,匿名审稿专家及编辑部老师对本文提出的修改意见与建议,对文章质量的提升大有益处,在此一并表示感谢!
曹建平, 祝意青, 韩美涛, 等. 陕西重力网优化改造及监测能力评估[J]. 地震地磁观测与研究, 2014, 35(Z1): 165-170. |
陈石, 王谦身, 祝意青, 等. 青藏高原东缘重力导纳模型均衡异常时空特征[J]. 地球物理学报, 2011a, 54(1): 22-34. |
陈石, 王谦身, 徐伟民, 等. 华北地区热均衡、重力均衡与深部构造[J]. 地球物理学报, 2011b, 54(11): 2864-2875. |
陈石, 王谦身, 祝意青, 等. 汶川MS 8.0震前区域重力场变化与震质中研究[J]. 地球物理学进展, 2011c, 26(4): 1147-1156. |
陈石, 王青华, 王谦身, 等. 云南鲁甸MS 6.5地震震源区和周边三维密度结构及重力场变化[J]. 地球物理学报, 2014, 57(9): 3080-3090. |
陈石, 徐伟民, 蒋长胜. 中国大陆西部重力场变化与强震危险性关系[J]. 地震学报, 2015, 37(4): 562-574. |
陈运泰, 顾浩鼎, 卢造勋. 1975年海城地震和1976年唐山地震前后的重力变化[J]. 地震学报, 1980, 2(1): 21-31. |
杜建军. 渭河盆地东南缘主要断裂晚更新世以来的活动性及灾害效应[D]. 北京: 中国地质科学院, 2016.
|
范美宁. 欧拉反褶积方法的研究与应用[D]. 吉林大学, 2006.
|
高倩, 陈石. 基于欧拉反褶积方法计算川滇交界重力变化场源特征[J]. 地球物理学进展, 2015, 30(2): 503-509. |
管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005.
|
刘芳, 祝意青, 梁伟锋, 等. 基于欧拉反褶积方法估算华北地区重力变化的等效源参数[J]. 地震, 2016, 36(4): 163-170. DOI:10.3969/j.issn.1000-3274.2016.04.014 |
鲁宝亮, 范美宁, 张原庆. 欧拉反褶积中构造指数的计算与优化选取[J]. 地球物理学进展, 2009, 24(3): 1027-1031. DOI:10.3969/j.issn.1004-2903.2009.03.029 |
马宗晋, 高祥林, 宋正范. 中国布格重力异常水平梯度图的判读和构造解释[J]. 地球物理学报, 2006, 49(1): 106-114. DOI:10.3321/j.issn:0001-5733.2006.01.015 |
申重阳, 李辉, 孙少安, 等. 2008年于田MS 7.3地震前重力场动态变化特征分析[J]. 大地测量与地球动力学, 2010, 30(4): 1-7. |
申重阳, 谈洪波, 郝洪涛, 等. 2009年姚安MS 6.0地震重力场前兆变化机理[J]. 大地测量与地球动力学, 2011, 31(2): 17-23. |
石磊, 郭良辉, 孟小红. 估计磁场源位置的倾斜角梯度算法改进[J]. 物探与化探, 2012, 36(2): 287-292. |
王卫东. 西安地裂缝形成的区域稳定性动力学背景研究[D]. 长安大学, 2009.
|
姚长利, 管志宁, 吴其斌, 等. 欧拉反演方法分析及实用技术改进[J]. 物探与化探, 2004, 28(2): 150-155. DOI:10.3969/j.issn.1000-8918.2004.02.017 |
翟丽娜, 贾晓东, 焦明若, 等. 基于欧拉反褶积方法计算辽宁地区重力变化场源特征[J]. 地震研究, 2020, 43(2): 388-393. DOI:10.3969/j.issn.1000-0666.2020.02.022 |
张永奇, 曹建平, 郝洪涛, 等. 陕西地区流动重力历史资料清理分析[J]. 地震地磁观测与研究, 2014, 35(Z1): 171-176. |
郑秋月, 王青华, 刘东, 等. 基于时变重力数据的川滇地区场源模型反演与解释[J]. 地震, 2021, 41(1): 205-218. |
祝意青, 徐云马, 吕弋培, 等. 龙门山断裂带重力变化与汶川8.0级地震关系研究[J]. 地球物理学报, 2009, 52(10): 2538-2546. DOI:10.3969/j.issn.0001-5733.2009.10.012 |
祝意青, 梁伟锋, 赵云峰, 等. 2017年四川九寨沟MS 7.0地震前区域重力场变化[J]. 地球物理学报, 2017, 60(10): 4124-4136. DOI:10.6038/cjg20171037 |
祝意青, 张勇, 张国庆, 等. 21世纪以来青藏高原大地震前重力变化[J]. 科学通报, 2020, 65(10): 622-632. |
Chen Shi, Liu M, Xing L, et al. Gravity increase before the 2015 MW 7.8 Nepal earthquake[J]. Geophysical Research Letter, 2016a, 43. DOI:10.1002/2015GL066595 |
Chen Shi, Jiang C S, Zhuang J C. Statistical evaluation of efficiency and possibility of earthquake predictions with gravity field variation and its analytic signal in western China[J]. Pure and Applied Geophysics, 2016b, 173(1): 305-319. DOI:10.1007/s00024-015-1114-x |
Pavlis N K, Holmes S A, Kenyon S C, et al. The Development and Evolution of the Earth Gravitational Model 2008 (EGM2008)[J]. Journal of Geophysical Research, 2012, 117: B04406. |
Reid A B, Allsop J M, Granser H, et al. Magnetic interpretation in three dimensions using Euler deconvolution[J]. Geophysics, 1990, 55(1): 80-91. DOI:10.1190/1.1442774 |
Sandwell D T, Smith W H F. Global Marine Gravity from Retracked Geosat and ERS-1 Altimetry: Ridge Segmentation Versus Spreading Rate[J]. Journal of Geophysical Research: Solid Earth, 2009, 114(B1). |
Thompson D T. EULDPH: A new technique for making computer-assisted depth estimates from magnetic data[J]. Geophysics, 1982, 47(1): 31-37. DOI:10.1190/1.1441278 |
 2021, Vol. 42
2021, Vol. 42

