2. 中国武汉 430071 中国地震局地震研究所;
3. 中国武汉 430071 中国地震局地震大地测量重点实验室
2. Key Laboratory of Earthquake Geodesy, Institute of Seismology, China Earthquake Administration, Wuhan 430071, China;
3. Key Laboratory of Earthquake Geodesy, China Earthquake Administration, Wuhan 430071, China
地震波在地球介质中经多次散射形成尾波。尾波在地球介质中传播时间长,由于重复采样、叠加和放大作用,其对介质的微小变化更加敏感,能识别直达波不能识别的介质的细微变化(张金川等,2014)。基于该特性,可利用尾波干涉方法识别震源、散射体位置、地震波速度与介质的细微变化,并广泛应用于断层活动性、工程材料检测、冰川活动、火山监测等领域(肖卓等,2015)。近年来,诸多地震学者利用尾波干涉方法开展了一系列研究,如:宋丽莉等(2012)通过室内试验,利用尾波干涉方法观测到直达波难以分辨的岩石物性变化;张金川(2014)利用尾波干涉技术研究广西龙滩水库重复地震,发现散射体运移可能与库水向地下裂隙中的运移有关;肖卓等(2016)运用尾波干涉技术分析2014年云南盈江双震期间地壳介质状态的变化;李乐等(2017)利用重复地震尾波研究汶川强震破裂区震后波速的微变化;鲍子文(2019)利用重复地震尾波研究安徽霍山地区介质变化,发现地震波速度存在季节性变化,与大气降水有较好的相关性。
2017年11月23日17时43分,重庆武隆区发生MS 5.0地震。该地震事件是有地震仪器记录以来重庆渝东南地区发生的最大地震。文中利用尾波干涉原理,研究武隆MS 5.0地震发生后,余震期间震源区地下介质的变化,有助于了解强震发生时地壳介质性质和应力状态的变化。
1 资料选取武隆区地处重庆市东南部,位于乌江下游峡谷区,岩石成分以碳酸盐、砂岩和页岩为主,岩溶地貌发育,形成大量溶洞群、天坑群、地缝等自然景观。该地区附近分布方斗山基底断裂、七曜山—金佛山基底断裂及彭水基底断裂,中小断裂有三会冲断裂、芙蓉江断裂、文复断裂、马武断裂、火石垭断裂、郁山断裂、和尚岩断裂(戴应洪等,2020)(图 1)。李翠平等(2019)分析认为,震中附近流体的深部渗透作用导致局部断层活化,诱发此次武隆MS 5.0地震,发震断层与文复断裂关系较为密切。
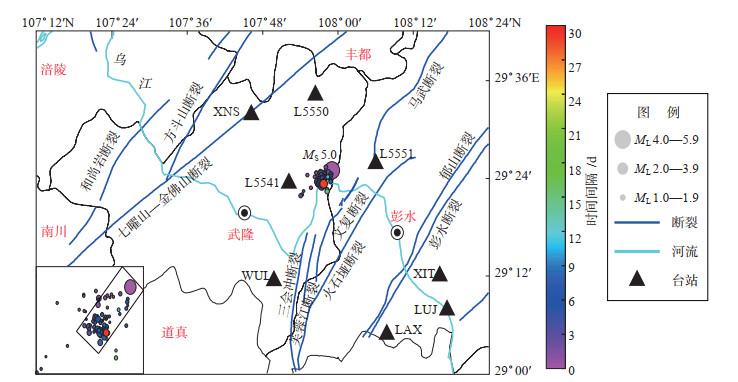
|
图 1 研究区地震台站、震中及区域构造 Fig.1 Seismic stations, epicenters, and regional structure in the study area |
武隆MS 5.0地震发生后,在震中附近架设3套流动台(L5541、L5550、L5551),均配备短周期地震计(采样率100 Hz),进行地震监测。各流动台台基噪声测试参数见表 1,可见环境地噪声水平均在Ⅱ级或以上。截至12月23日,重庆数字地震台网共记录到武隆及邻区(29°00′—29°42′N,107°12′—108°24′E)发生ML≥1.0地震108次(含MS 5.0主震),最大余震为2017年11月29日10时34分武隆ML 3.1地震。选取108次ML≥1.0地震波形数据和观测报告,分析地壳介质变化。
| 表 1 流动台站台基噪声参数 Table 1 Noise parameters of three mobile stations |
重复地震概念于20世纪60年代被提出,目前尚无统一定义(李宇彤等,2011),Nadeau等(1995)将发生在同一断层位置,震级和复发间隔相近,震源机制与波形高度相似的一组地震称为重复地震。Schaff等(2004)则将重复地震定义为被至少一个台站记录到,且波形相关系数不小于0.8的地震对事件。文中通过计算波形互相关系数(cross-correlation简称cc)和约束震源位置的方法,来挑选武隆MS 5.0地震发生后的重复地震。
2.1 地震序列重定位汪建等(2020)利用武隆地区2010—2017年重复地震和观测报告资料,发现该区地震定位和震相拾取精度较高。为得到更精确的震源位置,利用双差定位法,采用武隆地区精细地壳速度结构模型(表 2)(王小龙等,2013),对所选108次地震序列进行重定位。双差定位结果显示,MS 5.0主震发生在三会冲、芙蓉江、文复断裂与马武断裂交汇部位,震中位于乌江上游彭水电站与下游银盘电站水位段之间,与乌江水系最近距离约2 km,震源深度约10 km,余震序列呈条带分布,与附近断裂走向平行,地震序列破裂面呈NE—SW向单侧破裂(图 1)。
| 表 2 武隆地区速度结构模型(据王小龙等,2013) Table 2 The seismic velocity model used in the location (According to Wang Xiaolong et al, 2013) |
将地震波形转换为SAC格式,选取垂直分量,进行去倾斜、去线性趋势及0.5—10 Hz带通滤波预处理(汪建等,2018),挑选重复地震,步骤如下:①计算同一台站中任意2个地震波形的互相关系数,计算起点为P波到时前1 s,计算长度选择4倍Sg、Pg震相走时差;②找出同时被3个台站(L5541、L5550、L5551)记录且各台互相关系数(cc)≥0.9的地震对事件作为相似地震;③结合双差定位结果,寻找间距(不考虑震源深度的影响)小于1 km的相似地震。
经挑选,得到3组满足条件的地震对,均包含2个地震事件。重复地震以D1、D2、D3编号,主震设为D0。重复地震与流动台站分布见图 2,可见D1、D2、D3均分布在主震D0南侧,由北向南依次扩展,结合发震时刻可知,重复地震对均发生在余震活动相对减少阶段。
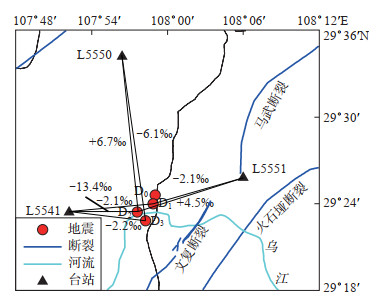
|
图 2 台站与重复地震分布 Fig.2 Distribution of seismic stations and repeating earthquakes |
对武隆MS 5.0地震序列重复地震对参数信息进行统计,结果见表 3,可知:D1、D2、D3的震级均小于ML 2.0,震级差值最大ML 0.5,最小ML 0.3;震源深度差值最大2 km,最小1 km;地震对重复周期具有明显变化,时间间隔从十几小时至几天不等,最大间隔近4天,D1、D2时间间隔相近。
| 表 3 武隆MS 5.0地震及重复地震对的参数统计 Table 3 Parameter statistics of the Wulong MS 5.0 earthquake and repeating earthquakes |
Snieder(2002)基于前人研究提出尾波干涉方法,并对其原理进行了系统阐述。尾波干涉法基于路径叠加理论,认为波场是沿可能散射路径传播的子波的叠加,重复地震与台站之间的传播路径大致相同,波形差异由介质变化所引起,重复地震尾波的变化反映了以台站和重复地震为焦点的椭球体上介质的变化,可以利用重复地震尾波研究地壳介质的波速变化,进而分析引起波速变化的原因(肖卓等,2016)。
波形数据原始采样率为100 Hz,即两列波形走时延迟最小为0.01 s。为获得更小的走时延迟,在尾波干涉测量之前,采用插值法将原始信号的采样率提升至10 000 Hz(Peng et al,2006),即两列波形的走时延迟最小为0.000 1 s。当波速在介质中发生变化时,重复地震的尾波穿过该介质时也将发生走时扰动,在接收点表现为波形的走时偏移。文中采用移动窗口互相关法(Niu et al,2003;肖卓等,2016)计算重复地震之间的走时偏移,即将发震时刻较早的重复地震当作参考地震,从P波初至到时起算,对重复地震进行尾波干涉分析。通过移动时间窗,计算每一个时间窗内波形的走时延迟,得到走时延迟及不相关系数随流逝时间的分布。结合前人经验(张金川,2014;肖卓等,2016),选取P波初至到时至S波到时的2倍加4 s作为尾波干涉测量窗口,移动窗口长度为1 s,移动步长为0.05 s,即每1 s内有20个干涉测量点。
假设介质中波速变化是均匀的,若波速下降(增大),则两列波形的走时偏移将随着流逝时间线性上升(减小)(Snieder,2006)。设原始波速为v,介质整体发生大小为δv的波速变化,则走时偏移τ与波速变化δv的对应关系(Snieder,2006;Payan et al,2011)为
| $ \frac{{\delta v}}{v} = - \frac{\tau }{t} $ | (1) |
式中,走时偏移τ与流逝时间t经线性拟合得到的直线斜率即为介质波速的相对变化。在计算每小时时间窗j内波形的走时偏移τj时,其测量误差估计(Liu et al,2010)为
| $ {E_{\delta v/v}} = \sqrt {\frac{{{\eta _\tau }}}{{\sum\limits_{j = 1}^M {t_j^2} }}} $ | (2) |
式中,tj为小时间窗j的中心位置,M为时间窗的数量,ητ为拟合残差,表示为
| $ {\eta _\tau } = \frac{{\sum\limits_{j = 1}^M {} {{({\tau _j} - {t_j}\frac{{\delta v}}{v})}^2}}}{M} $ | (3) |
测量误差下限στ需满足Cramer-Rao Lower Bound法则(Quazi,1981;Carter,1987),公式如下
| $ {\sigma _\tau } \ge \sqrt {\frac{3}{{2f_0^3\pi T({B^3} + 12B)}}[\frac{1}{{{\rho ^2}}}(1 + \frac{1}{{{\rm{SNR}}}}) - 1]} $ | (4) |
式中,f0为信号主频,B为信号的频宽与主频之比,T为窗口长度,ρ为波形相关系数,SNR为信噪比。f0和B由波形数据控制,测量误差主要取决于互相关系数与信噪比,选取互相关系数及信噪比较高的尾波段进行尾波干涉测量较为合理(肖卓等,2016)。
3.2 尾波干涉结果利用上述原理,采用尾波干涉技术,分别对重复地震对D1、D2、D3在3个流动台的波形记录进行尾波干涉处理。
3.2.1 L5541台站记录尾波干涉处理。分别对重复地震对D1、D2、D3在L5541台的记录进行尾波干涉处理,结果见图 3、图 4、图 5(0 s设为P波初至到时)。
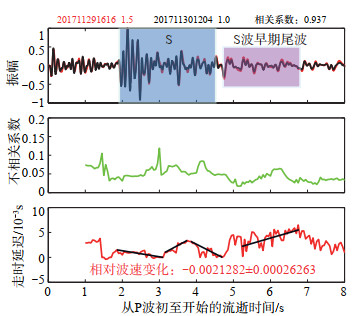
|
图 3 L5541台站D1波形记录及其不相关系数和走时延迟随流逝时间的变化 Fig.3 The seismic waveforms, uncorrelation coefficient and delay time of D1 repeating earthquakes with time at the L5541 station |
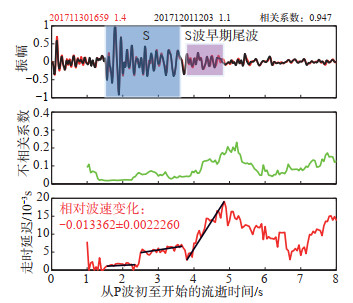
|
图 4 L5541台站D2波形记录及其不相关系数和走时延迟随流逝时间的变化 Fig.4 The seismic waveforms, uncorrelation coefficient and delay time of D2 repeating earthquakes with time at the L5541 station |
|
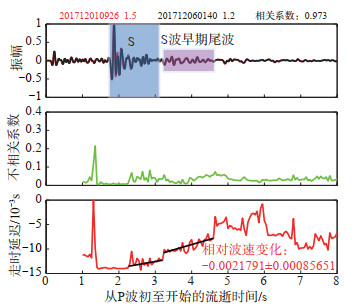
图 5 L5541台站D3波形记录及其不相关系数和走时延迟随流逝时间的变化 Fig.5 The seismic waveforms, uncorrelation coefficient and delay time of D3 repeating earthquake with time at the L5541 station |
(1)重复地震对D1。D1的2次地震分别发生在主震D0后第7和第8天,分析L5541台站的2次地震预处理波形及其不相关系数和走时延迟随流逝时间(从P波初至到时起算)的变化,结果见图 3。重复地震对D1的2次地震事件震级相差不大(0.5),但其相关系数却达0.937。由图 3可见:①在P波后续部分(1.00—1.95 s),走时延迟基本保持不变,后迅速下降至零值附近波动;②在S波振幅较大部分(1.95—3.20 s),走时延迟缓慢下降,S波后续部分(3.20—4.70 s)的走时延迟呈先增加后减小的变化趋势;③随着流逝时间的增加,S波早期尾波段(5.25—6.75 s)走时延迟明显增加,意味着波速的减小,S波尾波后续部分(6.75—7.75 s)的走时延迟明显减小,最大走时延迟约65×10-3 s;④结合移动窗口内波形的信噪比、不相关系数和走时延迟的线性变化规律,选取S波早期尾波段(5.25—6.75 s),由式(1)计算得到,其相对波速变化约为2.1‰。
(2)重复地震对D2。D2的2次地震分别发生在主震D0后第8和第9天,图 4给出重复地震对D2在L5541台站的尾波干涉结果。由图 4可见:①在P波后续部分(1.00—1.55 s),走时延迟迅速下降至零值附近波动;②在S波振幅最大部分(1.55—2.40 s),走时延迟基本保持不变,随着流逝时间的增加,S波后续部分(2.50—3.75 s)的走时延迟有缓慢增加的趋势;③在S波早期尾波段(3.80—4.90 s),走时延迟明显增加,变化较为线性,S波尾波后续部分(4.90—6.35 s)的走时延迟明显减小,最大走时延迟约19.1×10-3 s;④选取S波早期尾波段(3.80—4.90 s)计算其相对波速变化,结果约为13.4‰,波速变化较大。
重复地震对D2距L5541台站最近,传播路径不穿过乌江流域,可能受到断层挤压作用,岩石裂隙增多,导致地下介质剧烈变化,波速下降值较大。若选取S波后续部分(2.50—3.75 s)计算其相对波速变化,结果约1.4‰,约为S波早期尾波段计算结果的1/10,正是由于尾波的多次散射、叠加、放大,以及比S波更敏感的特点,尾波识别的波速变化比S波放大近10倍。
(3)重复地震对D3。D3的2次地震分别发生在主震D0后第9和第14天,图 5给出重复地震对D3在L5541台站的尾波干涉结果。由图 5可见:①S波衰减较快,在S波部分(2.35—3.25 s)走时延迟缓慢增加,在S波早期尾波段(3.25—4.60 s)走时延迟增加较为明显,S波后续尾波部分(4.60—7.35 s)走时延迟变化复杂,整体呈下降趋势。选取S波早期尾波段(3.25—4.60 s),计算得到其相对波速变化约为2.2‰;②在P波尾波部分(1.25—1.45 s)发现走时延迟和不相关系数均存在1个短周期“尖峰”(spike)变化,且变化比较尖锐,相比于P波尾波,S波及其尾波变化更为平滑。
Niu等(2003)在美国圣安德列斯断层帕克菲尔德区域,对重复微震进行数值模拟,发现若只是单一散射体的位置发生变化,走时扰动与不相关系数均将出现一个短周期的“尖峰”变化,若震源位置或介质波速发生变化,随着时间的流逝,走时扰动与不相关系数将呈现长周期变化趋势,根据实验结果,P波尾波的“尖峰”变化可能与地下介质中散射体的运移有关。由图 2可知,重复地震对D3到L5541台站的传播路径穿过乌江流域。该区岩溶发育,遍布溶洞和地下暗河,因S波不能在液体中传播,P波尾波出现的“尖峰”变化可能与震后库水在地下裂隙中的运移有关。
3.2.2 L5550台站记录尾波干涉处理。分别对重复地震对D1、D2、D3在L5541台的记录进行尾波干涉处理,可知D1在该台站尾波干涉结果未见明显变化,D2、D3的尾波干涉结果见图 6、图 7。

|
图 6 L5550台站D2波形记录及其不相关系数和走时延迟随流逝时间的变化 Fig.6 The seismic waveforms, uncorrelation coefficient and delay time of D2 repeating earthquakes with time at the L5550 station |
|
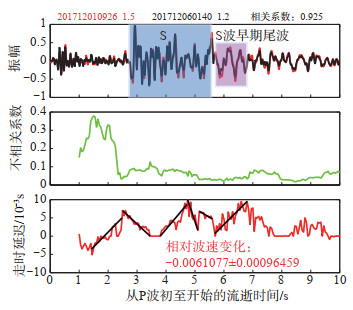
图 7 L5550台站D3波形记录及其不相关系数和走时延迟随流逝时间的变化 Fig.7 The seismic waveforms, uncorrelation coefficient and delay time of D3 repeating earthquakes with time at the L5550 station |
(1)重复地震对D2。图 6给出重复地震对D2在L5550台站的尾波干涉结果。由图 6可见:①在P波尾波部分(1.00—2.55 s)走时延迟无明显变化;②走时延迟在S波早期部分(2.55—4.00 s)减小,后续部分(4.00—6.05 s)增加,在S波早期尾波段(6.05—7.25 s)明显减小,意味着波速的增加,在S波后续尾波部分(7.25—9.40 s)保持在零值附近波动,最大走时延迟约为6.2×10-3 s;③选取S波早期尾波段(6.05—7.25 s)计算其相对波速变化,结果约为6.7‰,可能是由于此段波形相关系数不高,由式(2)—(3)计算,测量误差与波速变化在同一个数量级。
(2)重复地震对D3。图 7给出重复地震对D3在L5550台站的尾波干涉结果。由图 7可见:①P波尾波部分(1.00—2.70 s)的相关系数较低,走时延迟先增加后减小;②在S波部分(2.70—5.65 s),走时延迟变化复杂,呈减小—增加—减小的变化趋势,S波早期尾波段(5.75—6.85 s)走时延迟明显增加,变化较为线性,S波后续尾波部分(6.85—8.25 s)走时延迟下降至零值保持不变;③在不同波段(P、P尾波、S、S尾波),走时延迟的变化趋势不同且复杂,但在S波早期尾波段(5.65—6.85 s),走时延迟有明显增加,且较为线性,最大走时延迟约为9.5×10-3 s,其相对波速变化约为6.1‰。
3.2.3 L5551台站记录尾波干涉处理。分别对重复地震对D1、D2、D3在L5551台的记录进行尾波干涉处理,可知D3在该台尾波干涉结果未见明显变化,D1、D2的尾波干涉结果见图 8、图 9。
|
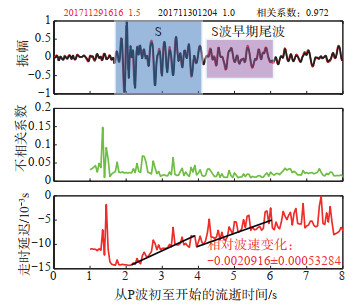
图 8 L5551台站D1波形记录及其不相关系数和走时延迟随流逝时间的变化 Fig.8 The seismic waveforms, uncorrelation coefficient, and delay time of D1 repeating earthquakes with time at the L5551 station |
|
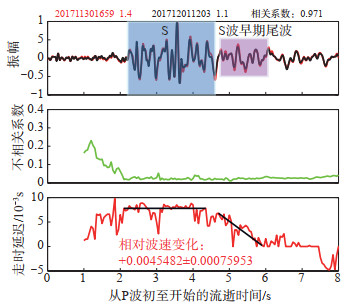
图 9 L5551台站D2波形记录及其不相关系数和走时延迟随流逝时间的变化 Fig.9 The seismic waveforms, uncorrelation coefficient, and delay time of D2 repeating earthquakes with time at the L5551 station |
(1)重复地震对D1。图 8给出重复地震对D1在L5551台站的尾波干涉结果。由图 8可见:①在P波尾波部分(1.35—1.75 s),发现走时延迟和不相关系数均存在2个短周期“尖峰”变化,S波及其尾波的走时延迟也有数个“尖峰”变化,但其最大变化幅度约为P波的1/3,根据Niu等(2003)的实验结果,此现象可能与震源位置或介质波速变化有关,若震源位置发生变化,直达波与尾波变化的量级应基本一致(Grêt et al,2006),假设由于介质波速变化导致P波尾波、S波及其尾波出现数个“尖峰”变化,则可能与地下介质的不均匀性或复杂性有关;②在S波及其尾波段(2.10—7.40 s),走时延迟整体呈上升趋势;③选取S波早期尾波段(4.00—6.05 s)计算其相对波速变化,结果约为2.1‰。
(2)重复地震对D2。图 9给出重复地震对D2在L5551台站的尾波干涉结果。由图 9可见:①P波尾波部分(1.00—2.10 s)相关系数不高,走时延迟变化较为复杂;②S波振幅较大部分(2.10—4.65 s)走时延迟基本保持不变,在S波早期尾波段(4.65—5.95 s)走时延迟明显减小,意味着波速的增加,在S波后续尾波部分(5.95—7.50 s)走时延迟保持在零值附近波动;③选取S波早期尾波段(4.65—5.95 s)计算其相对波速变化,结果约为4.5‰。
4 结论与讨论综上,绝大多数的测量误差比波速变化测量值小1个数量级,所得波速变化结果较为可靠。图 2可见,在L5541台站(距震源区最近),3组重复地震记录的S波尾波部分走时延迟均有明显增加现象,可能意味着地震波速的持续减小,其中D1和D3的波速相对变化小于3‰,D2的波速相对变化最大,约为13.4‰,意味着震源区附近岩石遭受破坏,结构弱化,应力得到较大释放;在D3的P波尾波部分发现了走时延迟和不相关系数均存在1个短周期“尖峰”变化,可能与库水在地下裂隙中的运移有关。在L5550台站,D2的S波尾波部分走时延迟明显减小,波速上升约6.7‰;D3的S波尾波部分走时延迟明显增加,波速下降约6.1‰,二者得到的波速变化值接近,可能表明震后局部地区地震波速度存在上升—下降的恢复过程,该阶段应力状态可能处于由累积到释放的快速调整过程。在L5551台站,D1的S波尾波部分走时延迟明显增加,波速下降约2.1‰;D2的S波尾波部分走时延迟明显减小,波速上升约4.5‰。
选取布设在武隆MS 5.0地震震中附近3个流动台的地震事件波形和观测报告,利用波形互相关技术,结合双差定位结果,选出3组符合条件的重复地震。利用尾波干涉原理,通过移动窗口互相关方法,计算了每组重复地震之间的走时延迟变化。尾波干涉结果显示,在P波的尾波部分,走时延迟变化较为复杂,可能与P波和S波不同的变化规律和PS转换波复杂的震相有关。在S波振幅较大部分,相关系数较高,走时延迟变化不大,可能是由于S波在重复地震识别过程中参与互相关计算的权重较高。在S波早期的尾波部分,走时延迟变化最为明显且较为线性,可能是由地壳介质的地震波速变化引起的。尾波干涉结果反映的是整个传播路径上介质变化的平均结果,距离震源区较远的XNS、LAX、XIT等台站,走时延迟变化并不明显,说明震源区外的地壳介质变化微弱。
选择流动台站的数据进行尾波干涉分析,优势在于流动台站距震中位置足够近,布局更加合理,且识别出的重复地震数量优于固定台站,更能捕捉到地下介质的细微变化。因武隆MS 5.0地震前近450天研究区内无地震记录,不能通过尾波干涉方法得到震前地下介质变化信息。
感谢江西省地震局查小惠工程师为本研究提供波形互相关和尾波干涉程序。
鲍子文. 利用重复地震研究霍山地区介质变化[J]. 国际地震动态, 2019(8): 47-48. DOI:10.3969/j.issn.0253-4975.2019.08.038 |
戴应洪, 于天航, 曹坤剑, 等. 重庆测震台网中心武隆MS 5.0地震监测情况及成因分析[J]. 防灾减灾学报, 2020, 36(1): 20-25. |
李翠平, 唐茂云, 郭卫英, 等. 2017年11月23日重庆武隆MS 5.0地震序列重定位及发震断层分析[J]. 地震地质, 2019, 41(3): 603-618. DOI:10.3969/j.issn.0253-4967.2019.03.005 |
李乐, 钮凤林, 陈棋福. 由重复地震的尾波研究汶川强震破裂区震后波速的微变化[C]//2017中国地球科学联合学术年会论文集(十二)——专题24: 青藏高原隆升与风化剥蚀和气候变化、专题25: 南北地震带强震活动的深浅部构造特征与动力学机制. 北京: 中国和平音像电子出版社, 2017: 324.
|
李宇彤, 蒋长胜. 波形相关意义"重复地震"研究综述[J]. 中国地震, 2011, 27(4): 335-347. DOI:10.3969/j.issn.1001-4683.2011.04.001 |
宋丽莉, 葛洪魁, 郭志伟, 等. 利用多次散射波监测介质性质变化的试验研究[J]. 岩石力学与工程学报, 2012, 31(4): 713-722. DOI:10.3969/j.issn.1000-6915.2012.04.010 |
汪建, 王同军, 杨亚运, 等. 利用重复地震观测重庆巫山地区地壳介质变化[J]. 地震地磁观测与研究, 2018, 39(6): 16-22. DOI:10.3969/j.issn.1003-3246.2018.06.003 |
汪建, 张巡, 杨亚运, 等. 重庆地区重复地震识别及在数字地震台网定位评价中的应用[J]. 地震地磁观测与研究, 2020, 41(2): 37-43. DOI:10.3969/j.issn.1003-3246.2020.02.005 |
王小龙, 马胜利, 郭志, 等. 利用地震背景噪声成像技术反演三峡库区及邻近地区地壳剪切波速度结构[J]. 地球物理学报, 2013, 56(12): 4113-4124. DOI:10.6038/cjg20131216 |
肖卓, 高原. 尾波干涉原理及其应用研究进展综述[J]. 地震学报, 2015, 37(3): 516-526. |
肖卓, 高原. 运用尾波干涉技术监测2014年盈江双震期间地壳介质状态的变化[J]. 地球物理学进展, 2016, 31(6): 2421-2428. |
张金川. 利用尾波干涉法研究水库蓄水引起的库区介质变化[D]. 北京: 中国地震局地震预测研究所, 2014: 73-74.
|
张金川, 王勤彩, 薛兵, 等. 用尾波干涉法监测介质波速变化研究进展[J]. 地震, 2014, 34(3): 62-73. |
Carter G C. Coherence and time delay estimation[J]. Proc IEEE, 1987, 75(2): 236-255. DOI:10.1109/PROC.1987.13723 |
Grêt A, Snieder R, Scales J. Time-lapse monitoring of rock properties with coda wave interferometry[J]. J Geophys Res Solid Earth, 2006, 111(B3): B03305.. |
Liu Z K, Huang J L, Li J J. Comparison of four techniques for estimating temporal change of seismic velocity with passive image interferometry[J]. Earthquake Science, 2010, 23(5): 511-518. DOI:10.1007/s11589-010-0749-z |
Nadeau R M, Foxall W, McEvilly T V. Clustering and periodic recurrence of microearthquakes on the San Andreas fault at Parkfield, California[J]. Science, 1995, 267(5197): 503-507. DOI:10.1126/science.267.5197.503 |
Niu F L, Silver P G, Nadeau R M, et al. Migration of seismic scatterers associated with the 1993 Parkfield aseismic transient event[J]. Nature, 2003, 426(6966): 544-548. DOI:10.1038/nature02151 |
Payan C, Garnier V, Moysan J. Determination of nonlinear elastic constants and stress monitoring in concrete by coda waves analysis[J]. European Journal of Environmental and Civil Engineering, 2011, 15(4): 519-531. DOI:10.1080/19648189.2011.9693344 |
Peng Z G, Ben-Zion Y. Temporal changes of shallow seismic velocity around the Karadere-Düzce branch of the north Anatolian fault and strong ground motion[J]. Pure Appl Geophys, 2006, 163(2/3): 567-600. |
Quazi A. An overview on the time delay estimate in active and passive systems for target localization[J]. IEEE Trans Acoust Speech Signal Process, 1981, 29(3): 527-533. |
Schaff D P, Richards P G. Repeating seismic events in China[J]. Science, 2004, 303(5661): 1176-1178. |
Snieder R. Coda wave interferometry and the equilibration of energy in elastic media[J]. Phys Rev E, 2002, 66(4 Pt 2): 046615. |
Snieder R. The theory of coda wave interferometry[J]. Pure Appl Geophys, 2006, 163(2/3): 455-473. |
 2021, Vol. 42
2021, Vol. 42

