0 引言

地震波的尾波因地球介质不均匀性而激发，表明地下介质具有非弹性特征。Aki等（1969，1975）用散射模型解释了尾波的形成和振幅衰减现象，尾波是地球介质中不均匀体对原生波的散射而产生的，岩石圈的不均匀性引发地震波散射形成了地方震的尾波，台站记录的延迟散射波就是地震尾波。考虑到台站和震源之间的距离，Sato等（1977，1980）在Aki模型基础上提出更符合实际情况、台源分离的单次散射模型。Q值是描述地下介质特性的一个参数。应力变化导致岩石性质发生改变，从而使得地震波传播的品质因子Q值发生变化。通过对Q值的分析和研究，可以了解地球内部热力学状态、介质特性以及地球结构的组成和变化。诸多研究利用地震发生前后地震尾波的衰减来分析Q_c值在时间上的变化特征，探究地震前兆信息，并发现尾波Q_c值与区域地震活动性有一定联系（啜永清等，2004；钱晓东等，2004；王勤彩等，2004；吕坚等，2007；张小涛等，2007；史水平等，2015）。研究发现，在同一研究区内，大震前尾波Q_c值普遍存在显著升高现象，并在主震后出现降低趋势；也存在尾波Q_c值在震前降低、震后升高或地震前后无变化的现象。

2016年10月20日在江苏省盐城市射阳县发生M_L 4.8（M_S 4.4）地震，发震地点在江苏省地震局划定的2017年度地震危险区内，震源深度25 km（缪阿丽等，2017），且震中附近部分地区震感强烈，附近县区震感明显，扬州、连云港地区部分有感（吴晓峰等，2019）。此为1992年M_S 4.6地震以来，该区发生的最大一次地震，地震序列为前震—主震—余震型（李迎春等，2018）。

以江苏省射阳地震台（下文简称射阳台）为中心点，选取2009—2018年台站周边200 km范围内M_L≥2.0地震波形资料，基于Sato单次散射模型，计算该区S波尾波Q_c值。由于此次M_L 4.8地震发生前射阳台测震波形较少，采用相同方法，选取2009年到2016年10月20日盐城、灌云地震台记录的地震波形资料，计算震前两台站地震S波尾波Q_c值，将3个地震台的计算结果进行对比，分析震前尾波Q_c值在时间上的变化特征，并探讨尾波Q_c值对于中强地震预报的意义。

1 构造背景

射阳台地处江苏盐城地区，位于南黄海盆地南部坳陷区，属长江中下游—南黄海地震带。该区地质构造较为复杂，众多断裂隐伏于第四系沉积层之下，主要断裂走向NE。该区以西分布郯庐断裂带，以东海域沿海岸线分布NW向苏北滨海断裂。目前有些断裂仍活动强烈，绝大部分中强地震即发生在断裂带附近。

苏北盆地地处郯庐断裂带以东、苏鲁造山带以南，是苏北—南黄海盆地西部的陆上部分，总体走向NE，延伸长度260 km以上，西窄东宽，由北向南依次分布盐城—阜宁凹陷、建湖隆起和东台凹陷。盐城—阜宁凹陷又划分为5个凹陷、3个凸起（舒良树等，2005）。该盆地内部各断陷盆地的边界断裂多为正断层，2016年射阳M_L 4.8地震（120.32°E，33.63°N）即发生在洪泽—沟墩断裂以南、盐城—南洋岸断裂以北的盐城凹陷内部，2条断裂走向均呈近NE向（李锋等，2017）。

2 方法原理

根据Sato单次散射模型，在一定振幅下，尾波振幅与时间的函数关系表达式为

$ \begin{array}{*{20}{l}} {F(t) = {\rm{lg}}[{{({A_{\rm{c}}}(t)/{A_{\rm{S}}})}^2}{K^{ - 1}}(a)] = C(f) - b(t - {t_{\rm{S}}})} \end{array} $

(1)

A_c(t)和K(a)分别由式（2）—（3）给出

$ {A_{\rm{c}}}(t) = {(A_T^2 - A_n^2)^{1/2}} $

(2)

$ \begin{array}{*{20}{l}} {K(a) = 1/a{\rm{ln}}[(a + 1)/(a - 1)]}&{a = t/{t_{\rm{S}}}} \end{array} $

(3)

式中：A_T为所取时间窗的平均振幅；为校正地震波噪声，A_n取P波到达前2 s内的平均振幅；t_S为S波到时，t为自发震时刻起算的尾波流逝时间；C(f)是与频率f有关的因子，在特定频率下视为常数。对于不同的频率点，利用式（1）拟合得到斜率b，以此得出该频率点的Q_c值，即b = 2πf lge/Q。根据每个频率点的Q_c值，最后拟合得到Q_c(f) = Q₀f^η。

3 资料处理

射阳地震台（下文简称射阳台）位于盐城市射阳县境内，海拔高度1.9 m。该台台基为第四纪松散沉积，地层厚度700—800 m。观测仪器配备如下：2009年6月—2015年11月，使用CMG-3TB型井下宽频带地震计，数据采集使用CMG-DM24数据采集器，采样率100 Hz，观测频带60 s—50 Hz；2015年11月，启用GL-S60B型井下宽频带地震计，数据采集使用EDAS-24GN数据采集器，采样率100 Hz，观测频带60 s—50 Hz。

考虑到信噪比问题，选取2009—2018年射阳台200 km范围内M_L 2.0以上地震波形资料，所选资料均为近震（地方震）记录，震相较清晰。

由于苏中沿海地区地质构造背景存在差异，在尾波流逝时间较长的情况下，尾波Q_c值结果稳定性较差（杨云等，2011）。根据射阳台实际情况，将尾波流逝时间窗长固定为30 s。截取6—18 Hz频率范围内的原始波形，以1 Hz为间隔频率，以[0.7f，1.3f ]为带宽，使用六阶Butterworth滤波器进行滤波。对滤波后波形，以S波初动点为起点，以0.5 s为步长，以2 s为窗长，向后滑动求取各时间点的平均振幅。

计算P波到达前2 s平均信号的背景噪声能量，以S波初至到时作为尾波起算时间，在30 s尾波流逝时间内，若地震波信号能量小于噪声能量，则剔除该条记录。数据处理后，取得46次地震波形，其中M_L 2.0—2.9地震27次，M_L 3.0—3.9地震17次，M_L 4.0—4.9地震2次，最大地震为2016年10月20日M_L 4.8地震。地震基本参数见表 1，均为中国地震台网公布的地震精定位结果，震中分布见图 1。取得的地震震中距最大184 km，最小6 km；震源深度最大27 km，最小4 km。

4 Q值计算及变化特征

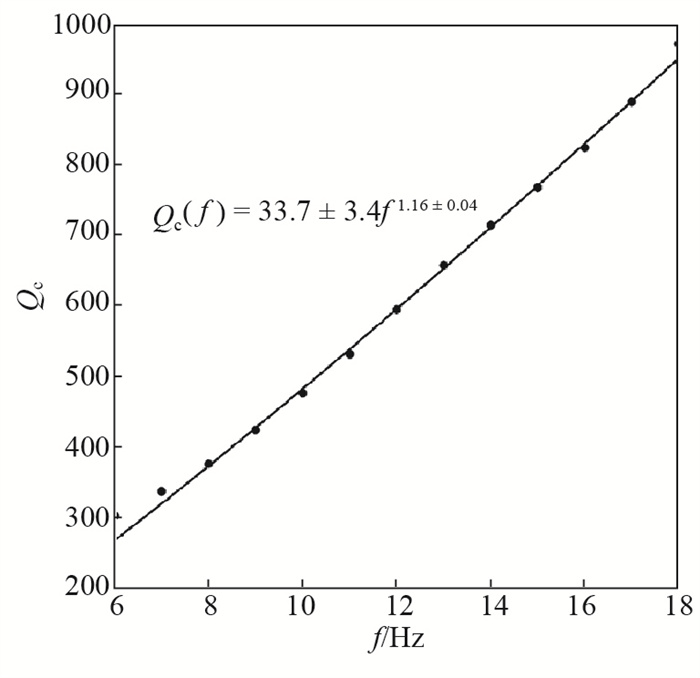
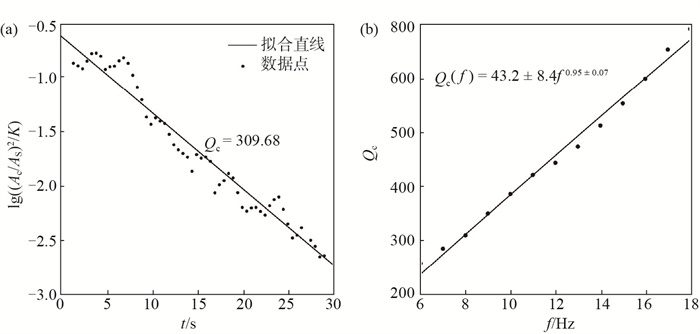
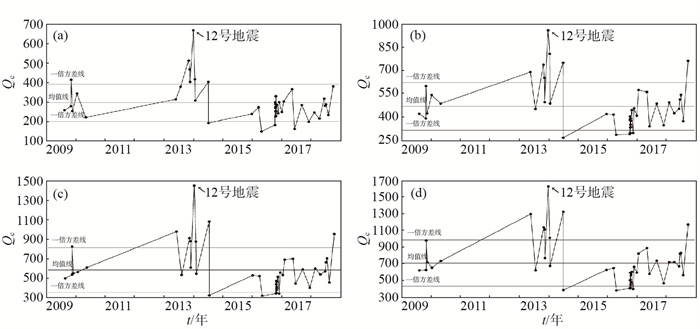
使用Sato单次散射模型，计算46次地震S波尾波Q_c值，以频率1 Hz时的Q_c值为Q₀值，各地震尾波Q值结果见表 1。采用最小二乘法进行拟合，得到射阳地区地震尾波Q_c值随频率的变化关系：Q_c(f) = 33.7 ± 3.4f^{1.16 ± 0.04}，见图 2。以2016年10月15日M_L 2.1地震为例，当f = 8 Hz时拟合得到尾波Q_c值，结果见图 3(a)；在不同频率点下，进行Q_c值拟合，拟合关系见图 3(b)。射阳地震序列尾波Q_c值在各中心频率点下随时间的变化特征较为一致。受篇幅所限，文中给出频率点为6 Hz、10 Hz、12 Hz、14 Hz时Q_c值演化示意图，见图 4。如4图中箭头所示，以2013年12月30日发生的12号地震（表 1中地震序号）为分隔点，前期地震尾波Q_c随时间变化起伏较大，且有逐渐走高趋势，此后地震Q_c值开始走低，且随时间变化相对平稳。

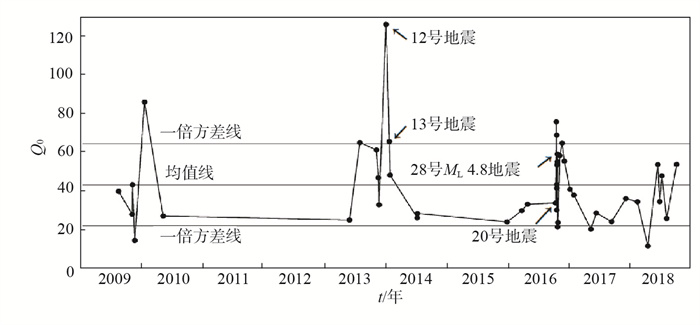
当f = 1 Hz时，得到射阳地区尾波Q₀值演变过程，见图 5，可见：12号地震发生前，地震尾波平均Q₀值为49.5，呈走高趋势；在2014年1月18日13号地震到2016年10月9日20号地震（表 1中地震序号）的发生时段内，地震尾波平均Q₀值为36.0，呈走低趋势；后直到2016年10月20日28号主震（表 1中地震序号）发生，地震尾波平均Q₀值为53.2，呈上升趋势。

5 Q值变化特征对比

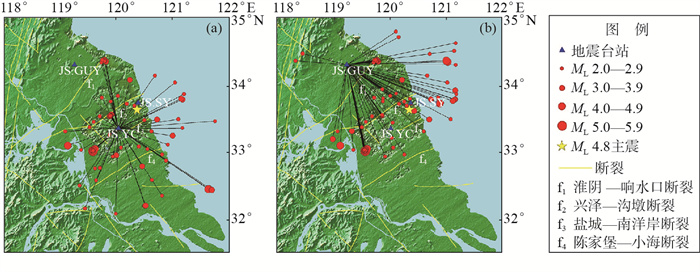
受测震仪器影响，2010—2013年射阳台测震波形较少，可能影响结果的精确性。为此，采用相同方法，数据处理后取得2009年至2016年10月20日盐城地震台（下文简称盐城台，位于射阳台西南方约50 km处）85条和灌云地震台（下文简称灌云台，位于射阳台西北方约120 km处）79条地震波形记录（图 6），探究射阳M_L 4.8地震前两台站记录尾波Q_c值特征，并将3个地震台站尾波Q₀值计算结果进行对比，结果见图 7。

由图 7可见：2012年11月4日以前，盐城台地震记录尾波Q₀值呈上升趋势，后逐渐下降，地震尾波平均Q₀值为86.3；2013年3月3日以前，灌云台地震记录尾波Q₀值呈不断走高趋势，其后下降，地震尾波平均Q₀值为52.9。因此，盐城、灌云台尾波Q_c值在2016年射阳M_L 4.8地震前4—5年，同样呈上升趋势，在震前2—3年，尾波Q_c值减小，变化趋势与射阳台较为一致。但是，二者Q₀最高值较射阳台出现得早，且数值更高，可能是因为，射阳台较早时期观测资料质量较低，可用波形数量较少，未较好反映该时段地震尾波Q₀值的变化。

总之，在射阳M_L 4.8地震前，盐城、射阳、灌云台所记录地震的尾波Q_c值在时间上均出现先上升后下降的长期趋势，即在震前出现明显的高值异常变化。

6 讨论

据Pulli（1984）和Chung等（2009）的研究，在尾波平均流逝时间t内进行采样，采样区域的椭球体平均深度为

$ h = {h_{{\rm{avg}}}} + {({a^2} - {r^2}/4)^{1/2}} $

(4)

式中，h_avg为平均震源深度；r为平均震源距；a是以震源和台站为焦点的椭球体表面投影的大半轴，可定义为vt/2，其中v为S波速度，在江苏地区地壳一般取为3.4 km/s。平均流逝时间为t = t_start + t_win/2，其中t_start为S波到时，t_win为尾波时间窗长。将上文3个台站的地震震源参数代入式（1），得到射阳、盐城和灌云台地震采样区域半径分别约为23 km、20 km、17 km的椭球体，椭球体中心位于台站与震源之间的中间位置，台站与震源相距分别约27 km、37 km、63 km。在此情况下，地震采样区域的椭球体在3个台站附近重叠，且台站记录的是不同方位角的近震（地方震）事件，计算得到的尾波Q_c值能较好反映椭球体重叠相近区域的应力变化。

对地震波衰减的研究可以揭示地壳应力的变化，以震源和台站为2个焦点的椭球范围内的品质因子尾波Q_c值对地壳应力变化反映敏感。尾波Q_c值与构造活动水平的相关性表明，地震尾波监测可以提供地震周期内区域构造应力变化引起的介质破裂的时间变化和能量衰减信息（Gholamzadeh et al，2014）。Aki（2004）认为，Q_c值变化与频率之间的关系源于地下断裂产生的散射衰减，破裂增多促使Q_c值减小，破裂愈合促使Q_c值增大。陈颙等（2001）认为，破裂会让流体渗入介质，导致介质的吸收衰减作用增强，Q_c值减小；而围压增大，促使介质的吸收衰减作用变弱，Q_c值增大。一般认为，构造活动稳定、地震活动相对平静的区域Q值高，介质的非均匀性低，传播过程中地震波能量衰减较慢；构造活动强烈、地震活动相对频繁的区域Q值低，介质的非均匀性高，传播过程中地震波能量衰减较快（Singh et al，1983；李白基等，2004）。

Jin和Aki（1989，1993）、Aki（1996）通过系统测量加州50多年来尾波Q^-1和地震活动性之间的关系，证明可以用Q^-1的时间变化与地震频率N(M_c)之间的强正相关，来解释地震区的地震活动性变化，并据此提出蠕变模型，即假设脆—韧性过渡带中存在具有地震区特有尺度特征的韧性断裂。一般来说，蠕变可能会因应力释放而降低地震活动性，但也可能会增强震级大小与应力集中引起的蠕变断裂尺度特征相当的地震发生的可能性。射阳地区所在下扬子区岩石圈流变学剖面为2层软的韧性层夹在3层较硬层之间的“3层状”结构，是一个特殊的低强度岩石圈类型（李成等，2001）。

研究结果显示，在2016年射阳M_L 4.8地震前3—6年（表 1中1—12号地震），该区地壳介质应力不断累积，且伴随M_L 3.0左右地震的发生，传播介质的均匀性和弹性提高，地震波在传播过程中能量损耗减小，Q_c值升高。在主震前约2年（表 1中13—20号地震），在较强应力作用下，岩石围压逐渐增高，特别是脆—韧性过渡带中韧性变形的能力增加，吸收衰减作用增强，尾波Q_c值下降，该阶段以M_L 3.0以下小震为主。此时，产生了与周围地震频率增加有关的相同尺度的应力集中，在前震发震期间，即主震临近破裂时（表 1中21—28号地震），短时间内的应力集中导致裂隙闭合，Q_c值稍有增大。主震发生后（表 1中29—36号地震），由于地壳应力得到释放，介质松弛破碎，流体渗入岩石间隙，地震波在传播时能量损耗增大，Q_c值相对较小，但地壳介质应力开始重新累积，2017—2018年（表 1中37—46号地震），Q_c值又逐步升高。可见，在此地震序列发生前，Q_c值具有上升—下降—上升—发震的变化特征。

从计算结果看，整个射阳地震序列的Q₀值较低，46个地震拟合所得Q₀值为33.7，表明盐城射阳沿海地区是江苏Q值较低区域，地震波能量衰减较快，松散覆盖层较厚，岩石圈强度低而不易积累能量；对频率的依赖性指数η为1.16，反映该区Q值对频率依赖性较强，浅层介质相对破碎，均匀程度较低，以小震活动为主，中等地震相对活跃。

7 结论

利用Sato单次散射模型和射阳台46条地震波形记录，研究射阳地震序列尾波Q_c值在时间上的变化特征，得出以下结论：射阳地区地震S波Q_c值与频率之间的关系为Q_c(f) = 33.7±3.4f^1.16±0.04，该区为Q₀低值区域，浅层介质破碎，岩石圈强度低，以小震活动为主，中等地震相对活跃；尾波Q_c值随时间的演化过程显示，在2016年10月20日射阳M_L 4.8地震前，Q_c值有增大现象，在地震序列前，Q_c值的变化特征为上升—下降—上升—发震，主震后该地区地壳介质应力开始重新累积，Q_c值又有逐步升高趋势，但无明显高值上升异常，地震活动尚处于相对平静时段。

并采用相同方法，计算2009年至2016年10月20日盐城台85条地震波形记录和灌云台79条地震波形记录的尾波Q_c值，与射阳台计算结果对比显示，在射阳M_L 4.8地震前，盐城、射阳、灌云台所记录地震的尾波Q_c值，均出现明显高值异常变化。

由于射阳台数字地震波形资料较少，本区域用于强震分析的震例较少，尾波Q_c值计算的影响因素较多，计算误差和相关研究分析有待积累资料进一步探讨。