鹤岗地震台(以下简称鹤岗台)是国家基准地震台,地处黑龙江省小兴安岭东南麓丘陵地区,台基岩性完整、稳定。在地质构造上,台站位于佳依断裂、青黑山断裂和黑龙江断裂的三角形区域内,该区断裂纵横交错,地质构造背景复杂。同时,作为煤炭工业型城市,鹤岗市矿山采掘活动可追溯到20世纪30年代。因此,该区成为黑龙江省孕育、发生天然地震、诱发地震的主要地域。鹤岗台不仅承担着全球地震观测任务,还肩负着鹤岗矿震活动监测任务。
地震震级(M)是地震三要素中重要参数之一,也是各级政府开展灾害救援的重要参数(刘瑞丰等,2018)。因此,及时准确地测定一个地震的震级大小尤为重要。根据地震波的类型不同,地震震级分为体波震级mb和面波震级MS,其中确定面波震级大小依赖于记录到的地震事件面波最大地动位移和周期。但在台站日常工作中发现,鹤岗台测定的远震面波震级MS(HEG)与中国地震台网中心(CENC)公布的正式地震目录中对应的面波震级MS(CENC)存在一定偏差,而且随着震中方位、震中距的不同而发生变化。消除震级偏差,找出偏差原因,给出震级校正值,在实际工作中具有一定意义。
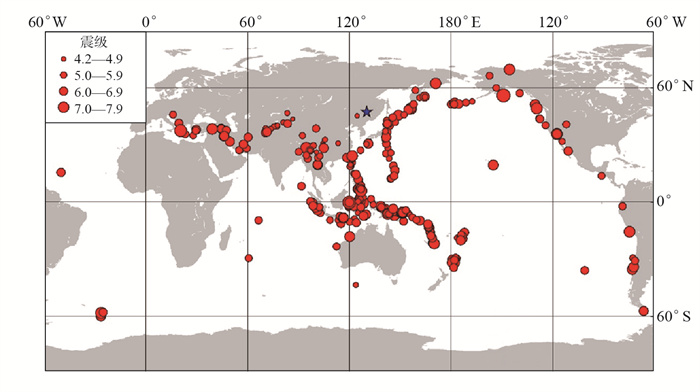
1 资料选取收集整理2018年1月—2020年3月鹤岗台甚宽频带数字地震计(CTS-1E)远震事件记录,筛选得到325次面波记录良好、震相清晰的事件,利用测震分析处理软件MSDP,重新测定面波震级,最小值4.2,最大值7.6,震中分布见图 1。以中国地震台网中心的发布震级为标准,计算二者的震级偏差,并分析偏差特性。
|
图 1 本研究所采用地震事件震中分布 Fig.1 Epicenter distribution map of earthquakes used in this study |
据中国新的震级国家标准GB17740—2017《地震震级的规定》(刘瑞丰,2017a)(以下简称新国标),面波震级测定公式为
| $ {M_{\rm{S}}} = \lg (\frac{A}{T}) + \sigma (\Delta) + C $ | (1) |
式中,A为地震事件波形记录中,NS向与EW向面波质点运动位移最大值矢量和的模,单位为μm;Δ为震中距,单位为弧度;T为水平向地动位移最大值对应的周期,单位为s;C为台基校正值;σ(Δ)为面波震级的起算函数,当2°<Δ<130°,σ(Δ) = 1.66lgΔ + 3.5;当130°<Δ<180°,σ(Δ) = 6.775 + 0.5[(2.147-0.4465Δ + 1.325)×(Δ - 90)10-2 + lgsinΔ + 3.5 + (lgΔ - 1.954)/3](何弈成等,2016)。
在地震参数逐步修订的动态过程中,由于使用的地震台个数和分布不同,且测定精度也越来越高,所以,会对最初速报震级进行修订,在正式地震目录中列出,供科学研究使用(刘瑞丰等,2018)。
2.2 震级偏差统计将筛选的325次远震面波震级数据,把鹤岗台MS(HEG)作为自变量,中国地震台网中心MS(CENC)为因变量,应用一元线性回归分析(何晓群等,2001),得到二者关系式,即
| $ \begin{array}{*{20}{l}} {{M_{{\rm{S}}\left({{\rm{CENC}}} \right)}} = {\rm{ }}0.9316{M_{{\rm{S}}\left({{\rm{HEG}}} \right)}} + {\rm{ }}0.8643} \end{array}\;\;\;{\sigma ^2} = 0.2633 $ | (2) |
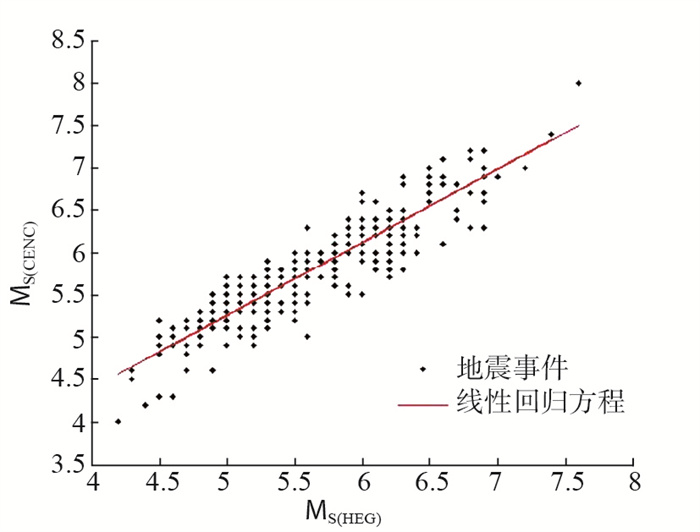
式中,σ2为回归方程的均方差。线性回归分析结果见图 2。对于选定的同一地震事件,计算鹤岗台与中国地震台网中心的面波震级偏差ΔM,公式如下
|
图 2 面波震级线性回归结果 Fig.2 Results of linear regression of surface wave magnitude |
| $ \Delta M = {M_{{\rm{S}}\left( {{\rm{HEG}}} \right)}} - {M_{{\rm{S}}\left( {{\rm{CENC}}} \right)}} $ | (3) |
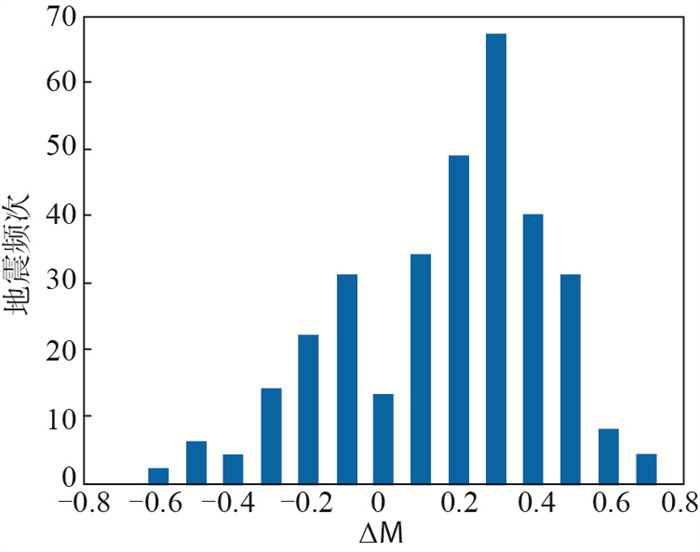
计算鹤岗台面波震级偏差ΔM,统计对应地震频次,结果见表 1。并由表 1结果绘制震级偏差直方图,结果见图 3,可见鹤岗台面波震级偏差整体基本符合正态分布,其中287次地震的震级偏差分布在-0.2—0.5,占地震总数的88%,表明鹤岗台测定的面波震级偏高。
| 表 1 震级偏差统计 Table 1 Statistics of magnitude deviation |
|
图 3 震级偏差直方图 Fig.3 Histogram of magnitude deviation |
计算所有震级偏差的平均值ΔM和标准误差δ,公式如下
| $ \Delta \bar M = \sum\limits_{}^{} {_{i = 1}^n} \Delta {M_i}/N $ | (4) |
| $ \delta = \sqrt {\sum\limits_{}^{} {_{i = 1}^n} {{(\Delta \bar M - \Delta {M_i})}^2}/(n - 1)} $ | (5) |
由式(4)、(5)计算得到:ΔM= 0.1681 ≈ 0.17,δ = 0.2685。可见,鹤岗台的测定震级MS(HEG)比中国地震台网中心的面波震级MS(CENC)平均约高0.17。
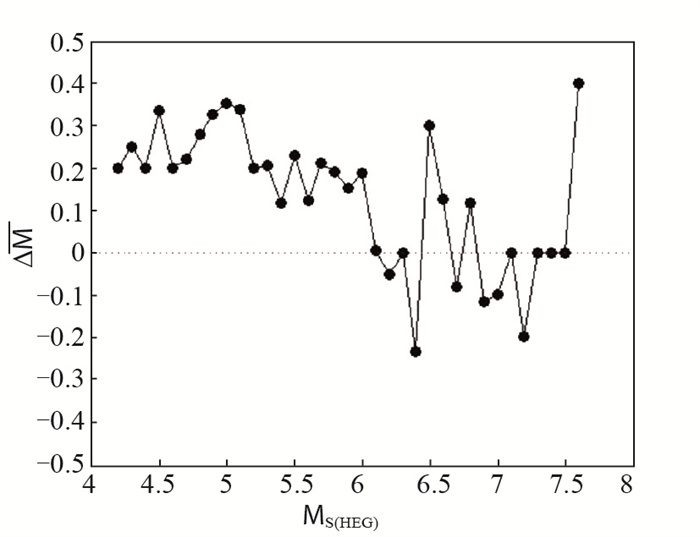
3 震级偏差分析 3.1 震级大小与震级偏差的对应关系以鹤岗台测定的面波震级MS(HEG)为横坐标,以0.1为单位间隔,统计对应震级偏差的算术平均值作为纵坐标,得到二者的对应关系,见图 4。由图 4可见:ΔM平均值在-0.23—0.4范围内变化;在本次研究中,面波震级MS集中分布在4.2—6.0范围内,与中国地震台网中心正式目录产出MS(CENC)相比,鹤岗台MS(HEG)偏大;当MS>6.0时,震级偏差ΔM变化无明显倾向性变化,可能由大地震样本数目不多所致,随着鹤岗台地震记录资料的积累,再进行探讨。
|
图 4 MS(HEG)震级大小与震级偏差对应关系 Fig.4 Relationship between magnitude and magnitude deviation |
已知震源经纬度和台站经纬度,计算震中距(Δ),单位弧度。对于选定的震例样本,在不同震中距范围内,统计平均震级偏差与对应的地震数,分析二者之间的关系,见表 2。由表 2可知:在各个震中距区间内,震级偏差均为正值,且随着震中距的增大而增大。究其原因可能是:①随着震中距的增大,地震波到达台站所经历的路径增长,穿过的地层也随之增多,地震波在地层中发生的反射、折射次数也增加,能量损失加大,造成测定台站面波记录在幅度和振幅周期上出现失真现象(田文德等,2012);②震中距大于90°的远震事件数量过少,且单台震级测定的起算函数与多台站不同。以上2点均为震级偏差的重要影响因素。
| 表 2 震级偏差与震中距的对应关系 Table 2 The relation between magnitude deviation and epicentral distance |
台站反方位角,也就是震中相对台站方位位置,是以台站为坐标原点,正北方向顺时针旋转到震中与台站的连线之间的角度。计算所选325次地震震中相对于鹤岗台的反方位角,以90°为间隔划分4个方位,统计不同方位的震级偏差平均值,见表 3。由表 3可知,除西北方位的平均震级偏差为负值外,其他3个方位均为正值。结合图 1可知,鹤岗台西北方位的地震发生在陆地,属于大陆型地震;其他方位震中多在西太平洋板块、印度洋板块、亚欧板块交界,属于海洋型地震。这就说明了,不仅地震波传播路径上的介质,震中的地理位置和震源区域地质背景和结构特征也是影响震级偏差重要因素(刘红桂,2012)。但若采用多台站测定震级取算数平均值,则可减少震中方向性对震级偏差的影响(中国地震局,2003)。
| 表 3 震级偏差与反方位角的对应关系 Table 3 Relationship between magnitude deviation and back azimuth |
通过对鹤岗台325次远震面波震级偏差进行分析,可以得出以下结论:①通过统计分析,鹤岗地震台测定的面波震级相对于国家台网中心公布面波震级偏高,震级偏差平均值小于0.2,符合规范要求;②从面波震级本身大小来分析,鹤岗台测定的面波震级MS在4.2—6.0范围内,与中国地震台网中心相比,震级偏大;③从震中距角度分析,震级偏差均为正值,而且随着震中距增大而增大;④从震中位置角度分析,海洋型地震震级偏差比大陆型地震大。
何晓群, 刘文 卿.. 应用回归分析[M]. 北京: 中国人民大学出版社, 2001.
|
何奕成, 秦磊, 立凯, 等. 连云港地震台面波震级偏差分析[J]. 地震地磁观测与研究, 2016, 37(6): 38-42. |
刘红桂. 不同构造区固有吸收衰减和散射衰减相对强弱的对比研究[J]. 国际地震动态, 2012(1): 31-32. |
刘瑞丰, 陈运泰, 许绍燮, 等. GB17740-2017地震震级的规定[S]. 北京: 中国标准出版社, 2017.
|
刘瑞丰, 陈运泰, 薛峰, 等. 如何正确使用新的震级国家标准[J]. 地震地磁观测与研究, 2018, 39(4): 1-11. |
田文德, 胡俊明. 成都台数字地震仪测定震级偏差分析与校正[J]. 四川地震, 2012(3): 20-23. |
中国地震局. 地震参数[M]. 北京: 地震出版社, 2003.
|
 2021, Vol. 42
2021, Vol. 42

