0 引言

天山地震带位于中亚地区，其南部为帕米尔高原和塔里木盆地，北部为哈萨克地台和准格尔盆地，沿东西方向可分为西天山、中天山和东天山，其中西天山和中天山主要位于吉尔吉斯斯坦和哈萨克斯坦境内，东天山则主要位于中国新疆地区（Lei，2011；孔祥艳，2019）。天山造山带古生代晚期在古亚洲洋闭合作用下形成，形变活动持续至中生代（Burtman，1975），在印度板块和欧亚板块碰撞的远程效应影响下，已被夷为平地的天山造山带新生代时期开始重新活动，发生内陆造山运动并再次强烈隆升，形成复活型内陆造山带（Molnar and Tapponnier, 1975；England and Houseman, 1985；Craig et al，2012）。

天山地震带的显著特点是，在南北两侧发育一系列与山体近乎平行的逆断层—褶皱带，同时在山体内部发育一系列NW向右旋走滑断层和NEE向左旋走滑断裂（Tapponnier and Molnar, 1979；沈军等，2003；Selander et al，2012；Campbell et al，2013；吴传勇，2016）。天山地震带及附近区域（72°—82°E，37.5°—42.5°N）（主要包含塔里木盆地、天山地震带中段至南段），自1997年伽师M_S 6.6强震群以来，发生多次中强地震，2020年1月19日伽师M_S 6.4地震的发生，表明该区域仍为新疆及附近地区中强地震活动频繁区域。

震例和实验研究均表明，随着大地震发生的临近，在相当大区域内应力场会发生长期变化，同时伴随大量地震活动（茂木清夫，1994）。对于小震活动而言，由于区域应力场及各地大小断裂的分布、数量和活动性质等影响因素较多，因此表现为小地震在时、空分布上常常出现某种异常的特征图像，其重要的一个共同点就是，地震活动从空间上的散乱随机趋向于特定图形分布（顾方琦，1985；朱传镇等，1988；蒋海昆，1992）。中强震前小震活动增强现象普遍存在，这种小震活动在空间格局上的变化，具有一定力学和构造不均匀性的物理基础，可能蕴含着地震孕育阶段的重要信息，具有深刻的物理内涵（梅世蓉等，1993；冯建刚等，2009；李永振等，2012）。

为定量描述地震在空间分布上的密集程度，王炜（1984）提出了地震空间集中度C值，认为某一区域一定时段内发生K次地震的单元面积的频次服从幂函数关系，并利用该方法对华北地区几次中强地震进行了回顾性研究，认为C值可用于中期地震预报（王炜，1984；Wang，1984；王炜，1986）。王力等（1989）则认为C值的计算速度和稳定性难以解决，进而提出一种简单图解法，并对四川几次大地震做了回顾性研究，发现震前震中附近区域确实存在C值的明显变化。王炜等（1989）进一步改进了C值的表示方法，以解决其计算过程中因参数选取对计算结果的影响及研究区域选取过于固定化等问题，分析认为，单位距离内某地震与其他地震的最短距离服从Weibull分布，在对华北地区中强地震的检验发现，该方法具有一定实际预报效能。但在对华北地区历史强震的震例进一步研究总结后，王伟等（1999）发现，异常持续时间和异常面积与主震震级无明显关系，且存在一定地震漏报现象（戴维乐等，1998；杜方等，2004）。

本文在前人研究的基础上，采用扩散链去余震方法，对中国大陆小震目录进行去余震处理，并计算1990年以来新疆地区C值空间分布，并对结果进行去背景计算，得出C值变化量，即ΔC值，对天山地震带及附近区域2000年以来发生的6级地震进行震例回溯，进而总结研究区域6级以上地震发生前ΔC值随时间的演化特征。

1 方法原理

空间集中度参数，即C值，能够表征小震的空间集中程度，是定量研究强震前小震空间集中分布特征的方法之一。王炜等（1989）认为，某一地震与其他地震的最短距离是在空间上量度地震是否集中的一个最简单的值。空间网格内地震之间的距离越小，意味着地震在空间分布上越集中。若网格内每一个地震与其他地震的最短距离为r，那么r服从Weibull分布，其概率密度函数为

$ f(r) = \mu {r^{\rho - 1}}{{\rm{e}}^{ - \mu {r^{\rho - 1}}/\rho }} $

(1)

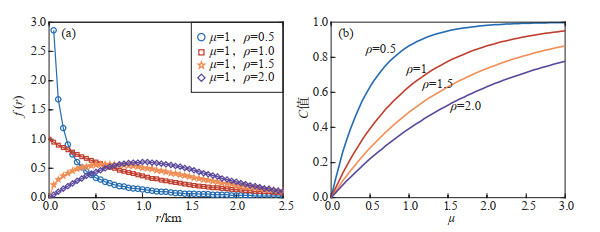
其中参数值与概率密度函数曲线关系表明，ρ的取值决定了概率密度函数曲线的基本形态，因此ρ和μ分别称为形状参数与尺度参数[图 1(a)]。当ρ＞1时，曲线中间部位f (r)具有最大值，类似于正态分布，表明震间距r的低值和高值较少，即地震分布相对均匀；当ρ = 1时，f(r) = μe^−μr，为负指数分布，同样表明地震分布相对均匀，但此时地震集中度略高于ρ＞1的情况；而当ρ＜1时，则表明震间距r的低值集中度高。

定义在单位距离内发生地震的概率为地震空间集中度C值（王炜等，1989），有

$ C = 1 - {{\rm{e}}^{ - \mu /\rho }} $

(2)

其中ρ和μ即为形状参数与尺度参数。上述讨论可知，当ρ＜1时，震间距r的低值相对较多，因此在μ的参数变化范围内，ρ＜1，C值始终最大，可认为，C值表征了地震在空间上的集中程度，即C值越大，地震集中程度越高[图 1(b)]。

由上述原理不难发现，当某区域内小震出现持续活跃情况时，其C值就会长时间持续高值。而在C值空间分布图中，由于涉及到统一图例，部分区域的长时间高值会严重影响震例的回顾性分析以及对未来地震预报规则的确定。因此，去除C值异常背景就显得尤为重要。

在本研究中，将同一网格内C值变化量定义为ΔC，背景异常设置为过去10年C值异常的均值，记为B_g，标准差记为σ，则有

$ \Delta C = \frac{{C - {B_{\rm{g}}}}}{\sigma } $

(3)

由式（3）可知，当C值与背景值的差异大于标准差时，表明此时ΔC值为空间集中度的变化异常。

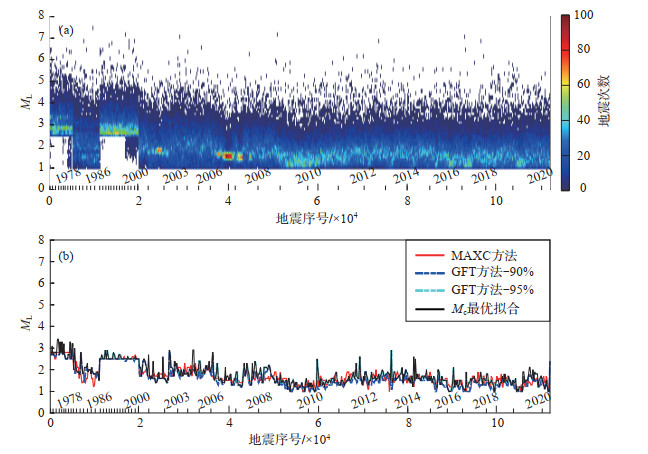
2 数据资料

天山地震带及附近地区（72°—82°E，37.5°—42.5°N）地质构造复杂，有历史记录以来大震频发（图 2）。2000年以来中国数字台网不断更新，地震监测能力大幅提升，但不同区域的监测能力在不同时段受地震台站分布密度影响而存在较大差异（冯建刚等，2012）。相对而言，天山地震带及附近地区地震台站分布不够均匀，且密度不大，而ΔC计算值则需要可信度高、记录相对比较全面的地震目录。文中采用中国地震台网中心提供的小震目录，在时空扫描过程中对小震目录完整性震级进行合理评估，从而保证扫描结果的稳定性。采用震级—序号法（Ogata et al，1991）、“最大曲率”MAXC方法以及拟合度分别为90%和95%的GFT方法（Wiemer and Wyss, 2000）进行最小完整性震级评估，计算结果显示，天山地震带2000年以来最小完整性震级在M_L 1.0—3.0之间波动，不同时段有差异，与李志海等（2011）的计算结果较一致。为保证计算结果的可靠性，文中采用M_L 3.0作为时空扫描的最小震级（图 3）。

据统计，1900—1985年天山地震带共发生7级以上地震11次，平均平静时间小于10年，而自1985年乌恰M_S 7.1地震发生以来（截至2020年），新疆地区7级以上地震平静时间已达35年之久。目前，天山地震带7级平静时间已远超历史平均平静时间。期间天山地震带6级地震活跃，自1985年乌恰7.1级地震至今已发生6级以上地震27次（表 1），2010年以来即已发生7次6级以上地震，最近一次为2020年1月19日伽师M_S 6.4地震，表明现阶段天山地震带仍处于中强地震活跃时段。

3 计算结果 3.1 空间集中度ΔC值时空扫描

在ΔC值计算过程中，余震会对计算结果产生较大影响。因此，采用扩散链法对中国地震台网中心给出的全国小震目录进行去余震处理，从而减小余震对结果的影响。进一步对选定的时空窗进行空间集中度时空扫描，从而得到C值时空演化图像。设定扫描过程中时空窗内统计地震的个数下限为30，若地震个数小于30，则不进行C值计算。具体扫描参数设定为：①地震目录震级下限为M_L 3.0，上限为M_L 4.0；②时间窗长为12个月；③时间扫描步长为1个月；④空间窗口半径为200 km；⑤空间扫描步长为0.5°×0.5°；⑥背景值和方差计算窗长为10年。

利用上述方法计算1990年以来新疆地区每月C值数据，建立C值文件数据库。在此基础上，搜索指定日期前10年的C值文件，计算并将文件中每个点的平均值作为该点背景值，同时计算标准差作为该点的标准差，用指定日期的C值数据减去背景值并除以标准差，得到ΔC值，因需减去背景值，所得结果为2000—2020年每月ΔC值，建立ΔC值文件数据库。

在震例扫描过程中，确定所研究的6级地震后，核实该地震前1年内震中附近区域是否存在ΔC值异常，确定异常演化范围，从上述文件库中提取相应时间段内异常区ΔC值，将ΔC≥0的部分求和，从而得到异常区时序曲线。

3.2 天山地震带6级以上地震前ΔC值演化特征

结合天山地震带完整性震级的变化（图 3），选取2000年以来11次6级以上地震进行回顾性研究，采用上述研究方法，计算震前震中附近区域ΔC值，结果表明，有5次地震发生前震中附近出现显著的ΔC值异常（表 2），而2012年新疆新源—和静交界M_S 6.6地震、2017年精河M_S 6.6地震以及2020年伽师M_S 6.4地震均在震前6个月出现ΔC值异常。

（1）2012年新疆新源—和静交界M_S 6.6地震。2012年6月30日5时7分，新疆新源、和静交界（43.4°N，84.8°E）发生6.6级地震，震源深度7 km，发震构造为伊犁盆地北缘断裂，震源机制显示为一次走滑型事件（魏芸芸等，2012）。震中及附近地区历史上中强地震比较活跃，1900年以来，震中附近100 km范围内发生5级以上地震18次，其中5.0—5.9级地震15次，6.0—6.9级地震1次，7.0级以上地震2次，分别为1906年12月23日沙湾西南7.7级和1944年3月10日新源东北7.2级地震，距离本次地震分别为20 km和90 km，时间最近的5级地震是2003年2月14日石河子5.4级地震，距离本次地震约84 km。

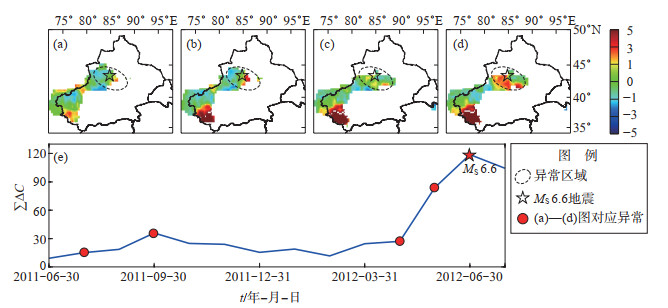
2012年新源—和静交界M_S 6.6地震前9个月，震中附近区域出现ΔC值异常，此时叶城至莎车区域也出现显著异常，但无对应的6.0级以上地震发生。由此次M_S 6.6地震前后ΔC值时空演化过程（图 4）可知，震中附近区域ΔC值在震前2个月无异常，震前一个月大幅升高。异常空间分布显示，震前震中附近ΔC值异常具有短期内强度和规模迅速增强的特点。从异常时序曲线可见，异常区域内部ΔC值累积和在2011年8月出现小幅升高，之后开始下降，2012年5月异常突然大幅升高，至发震当月达最高值，震后一个月开始下降（图 4）。

（2）2017年精河M_S 6.6地震。2017年8月9日7时27分，新疆博尔塔拉州精河县（44.3°N，82.9°E）发生6.6级地震，震源深度11 km。该地震发生在天山地震带北段，附近断裂为库松木契克山前断裂，震源机制显示为一次逆冲型地震（姜祥华等，2017）。1900年以来，该地震周边100 km范围内共发生5级以上地震18次，其中5.0—5.9级地震12次，6.0—6.9级地震5次，7.0级以上地震1次，为1944年3月10日新源7.2级地震，距离本次地震约93 km，时间最近为2016年2月11日新源5.0级地震，距离本次地震约93 km。

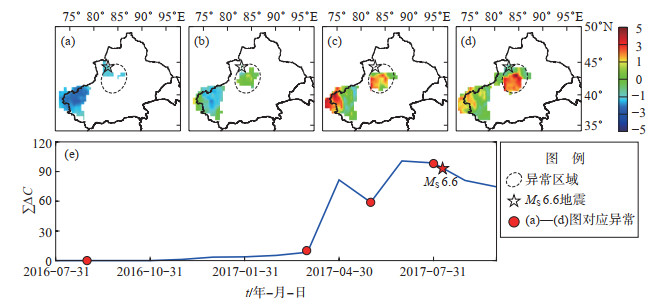
2017年精河M_S 6.6地震前5个月天山地震带北段未出现异常，震前4个月开始出现显著异常，至震前一个月，异常区域集中且无迁移现象（图 5，区域内异常值依次对应于(e)图中红色圆点）。从时序曲线看，震前5个月ΔC值累积和稍有升高，但不足以形成异常，震前4个月突然升高，随后稍有下降，震前2个月再次增强，持续至震前1个月，异常强度未发生变化，随即发生本次地震，震后异常强度开始下降。精河M_S 6.6地震前异常演化时间为4个月，且地震发生在异常区边缘，距离显著异常区约70 km（图 5）。

（3）2020年伽师M_S 6.4地震。2020年1月19日21时27分，新疆喀什地区伽师县（39.83°N，77.21°E）发生6.4级地震，震源深度16 km，发震断层为NEE走向的柯坪断裂，位于最南部柯坪塔格背斜西段，震源机制结果显示为逆冲兼走滑型破裂（孟令媛等，2020）。1900年以来，该地震震中附近100 km范围内发生5级以上地震98次，其中5.0—5.9级地震73次，6.0—6.9级地震24次，7.0级以上地震1次，为1902年8月22日阿图什8.3级地震，距离本次地震约87 km，时间最近为2003年2月24日巴楚M_S 6.8地震，距离本次地震约37 km，该区域还曾发生1997年M_S 6.6伽师强震群，距离本次伽师M_S 6.4地震约38 km。

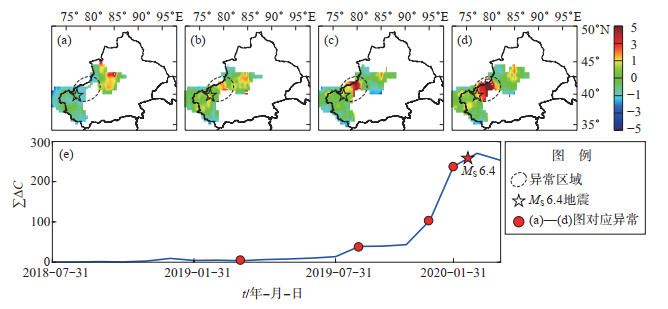
2020年伽师M_S 6.4地震前10个月，天山地震带北段ΔC值存在高值异常，震前5个月，高值异常区开始向南转移，使得天山地震带中部异常升高，震前2个月北段异常显著减弱，而中部地区异常持续增强，震前1个月天山中部异常显著升高且范围扩大，随即发生伽师M_S 6.4地震。从时序曲线看，震前2个月ΔC值累积和显著升高，至震前一个月持续增强，发震后次月异常开始减弱，整体演化过程持续5个月，异常集中且存在由北向南迁移的特点，伽师M_S 6.4地震震中位于异常边缘（图 6）。

4 讨论

计算新疆地区1990年以来小震空间集中度C值，发现异常具有空间分布不均匀特征，且局部地区存在长期高值现象，分析认为，主要原因在于未去除背景值的影响。因此，将C值的相对变化量定义为ΔC值，并对震例进行了回顾性研究。由天山地震带2000年以来11次6级地震前附近区域的ΔC值变化，可知：有5次地震前震中附近出现显著的ΔC值异常，有6次地震前未出现异常，漏报率为54.5%；而2000—2020年，天山地震带共出现10次显著异常，虚报率为50%。

（1）ΔC值异常演化空间分布特征。在5次ΔC值异常震例中，有2次属于其他区域迁移至发震地点的情况，但迁移距离较短；其余3次均为震源区出现异常且在短期内迅速增强后发震（表 2）。异常空间分布特征与王炜等（1999）的研究结果类似，即与1987年宁夏灵武5.2级地震、1989年山西大同5.7级地震等5次地震前约2年在震中附近出现的大面积C值异常类似。

（2）ΔC值异常时间演化特征。ΔC值异常的5次震例发生前，异常平均演化时间为8.6个月，仅2003年巴楚M_S 6.8地震前异常演化时间超过2年。其余4次震例异常演化时间均在1年以内，平均4.25个月，其中新源—和静交界M_S 6.6地震前异常演化时间最短，为1个月。

在研究过程中发现，采用区域变化的完整性震级计算ΔC值会出现异常不显著或无异常现象，而采用固定的完整性震级则会得到较好的扫描结果。此外，在参数扫描过程中，统计半径大小会对计算结果产生一定影响，实际处理发现，增大统计半径会使异常范围变大，而异常强度无明显变化，不利于震例总结以及预报工作中对后续强震地点的判断；对于样本统计的时间窗，若增加时间窗长，则样本量会增加，在已有样本量满足Weibull分布的情况下，样本量增加对计算结果影响不大，反之，则有可能使样本量不够而无法计算。目前的震例总结表明，时间窗长1年，计算结果对南天山西段2000年以来6级以上地震有一定指示意义。综上，由于异常扫描过程中时空窗等参数的选取对计算结果有一定影响，因此在计算ΔC值时有必要选择合理的参数。

研究结果表明，天山地震带ΔC值异常震例主要集中出现在2010年以后，初步分析认为，可能原因是，1990—2000年地震目录完整性震级大于M_L 3.0，其C值参与背景值计算，对2000—2009年的震例研究产生了影响。因此，需要对2000年以前天山地震带完整性震级进行系统化评估，以此为基础整理回溯2010年以前震例的ΔC值异常，更加系统地研究和总结天山地震带6级地震前ΔC值随时间的演化特征。

在论文撰写过程中，王海涛研究员、蒋海昆研究员、晏锐研究员、闫伟高级工程师和姜祥华博士给予指导和帮助，中国地震台网中心预报部地震学室的同事参与了讨论，在此一并表示感谢。