2. 中国北京 100081 中国地震局地球物理研究所
2. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China
在地震学历史上,Walke(1913)最先注意到P波初动的压缩与膨胀分布可能与地震有关联,日本志田顺(Shida,Toshi,1876—1936)最先确立P波初动的压缩与膨胀的四象限分布,而最先运用P波初动的压缩与膨胀四象限分布来探讨地震震源的性质,则是美国拜尔利(Byerly,Perry,1897—1978). 震源机制研究的近代发展始于1926—1928年,是拜尔利在研究1925年发生于美国蒙塔那(Montana)州的一次地震时(Byerly,1926),以及对1922年发生于智利的一次地震作类似的研究时开始的. 迄今拜尔利提出的这一利用P波初动压缩与膨胀分布研究地震震源机制的方法,已有将近一百年的历史. 一百年来,研究地震震源机制的方法,从利用P波初动的极性到S波的偏振,从体波到面波、到地球的自由振荡,从波形拟合到地震矩张量反演,从单纯的地震观测资料反演到地震资料与大地形变资料(GPS,InSAR,……,等资料)联合反演,从模拟记录地震图到数字记录地震图,从手工操作到计算机自动化处理,从少量、稀疏、分布不均匀的模拟记录地震图的分析处理到大量、密集、分布较均匀的地震台网、台阵数字地震记录资料的处理,有了很大的发展,但是最早采用来研究地震震源机制P波初动解的方法,由于这个方法所使用的资料仅仅是P波初动资料,比较简单易行,结果稳定可靠,所以至今仍在广泛使用.
国际上以及在国内,有关地震震源机制的理论和方法,已经有了不少优秀的论著和教材(例如,Honda, 1954, 1957, 1961, 1962;Кейлис-Борок,1957;克依利斯-博洛克,1961;Stauder,1962;Khattri,1973;Herrmann,1975;Brumbaugh,1979;Bullen and Bolt, 1985;Udias,1991;Bormann,2002;Udias et al, 2004;鲍曼,2006;等等). 考虑到国内有关专业结构和需求的差异,特撰写此份简明教材,作为地震震源机制理论和方法的入门及深造的向导,以适应不同专业背景(地震学、地球物理学、地质学、大地测量学、工程地震学、灾害科学、管理科学、……)、不同读者(学生、教师、管理人员、……)的不同需求(了解、学习、应用、……).
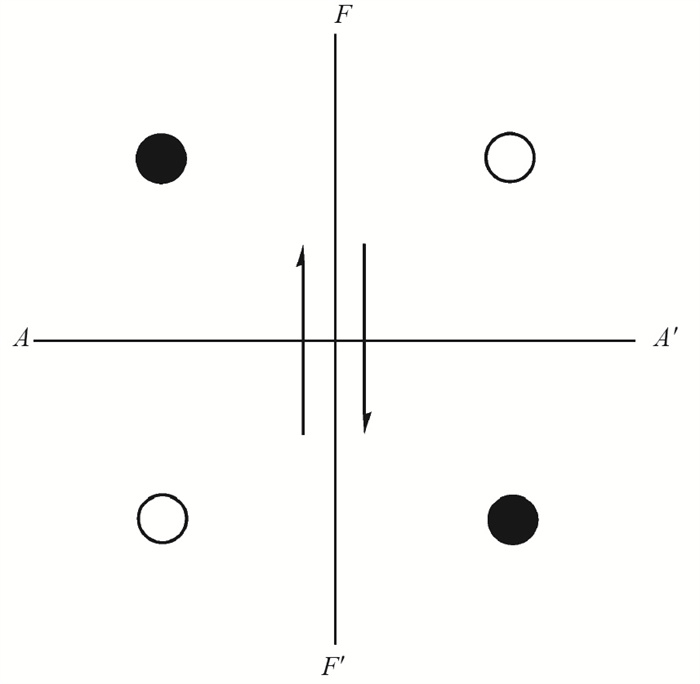
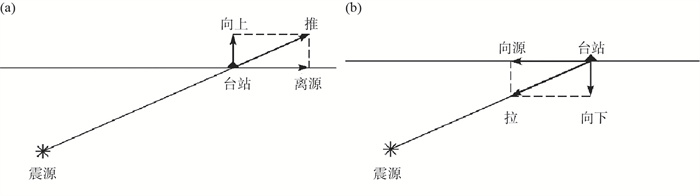
1 断层面解 1.1 P波初动的压缩与膨胀的分布图 1在平面上表示在一个垂直于地面的断层FF′上的纯粹水平运动,箭头表示断层两盘彼此相对运动. 直观地想像,地震波到达时,箭头前方的点最初应当是受到推动(push),或者说受到了压缩(compression);而箭头后方的点最初应当是被拉伸(pull),或者说朝震源发生了膨胀(dilatation);在竖直方向的运动则分别表现为向上(up)和向下(down);而在水平方向的运动则分别是离源(anaseismic)和向源(kataseismic)(图 2). 通常以push, C, u,a或“+”号表示初动是推、压缩、向上或离源,而以pull, D, d, k或“-”号表示初动是拉、膨胀、向下或向源. 在这种情况下,震源附近的区域被断层面FF′和与之正交的辅助面AA′分为四个象限. 在这些象限里,纵波即P波的初动交替地是压缩(图 1中以实心圆表示)或膨胀(以空心圆表示). FF′和AA′都是节平面,在这些面上,P波初动为零(Stauder,1962;Khattri,1973;Herrmann,1975;Brumbaugh,1979).
|
图 1 由一个垂直于地面的断层FF′的纯水平运动产生的地震P波初动的压缩(实心圆)与膨胀(空心圆)的分布 Fig.1 Distribution of compression (solid circle) and dilatation (open circle) of initial motion of seismic P waves resulting from pure horizontal motion FF′ a fault perpendicular to the ground |
|
图 2 压缩初动(a)与膨胀初动(b) Fig.2 First motions of compression(a) dilatation(b) |
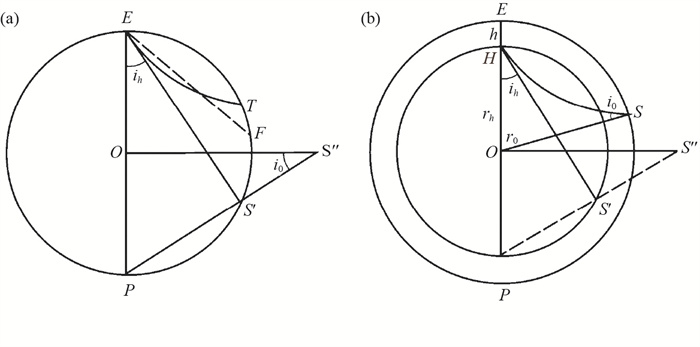
由于地球不均匀,地震射线发生弯曲. 射线弯曲导致离开断层时处于断层面一侧的地震射线最后可能到达断层面的另一侧. 图 3(a)中的E表示一个位于地面的震源,称为表面震源,其断层面为一个倾斜的平面EF. 在假定地球是均匀时预期沿直线ES′到达S′的射线将因地球不均匀、射线弯曲而到达断层面EF的另一侧. 于是,在预期接收到压缩初动的地方可能会接收到膨胀初动;或者反过来,在预期接收到膨胀初动的地方可能会接收到压缩初动. 这样一来就不再能用两个互相垂直的平面将压缩与膨胀隔开(Stauder,1962).
|
图 3 台站的延伸位置 (a) 表面震源;(b) 有一定深度的震源 Fig.3 The extended position of a station (a) For a surface source; (b) For any focal depth |
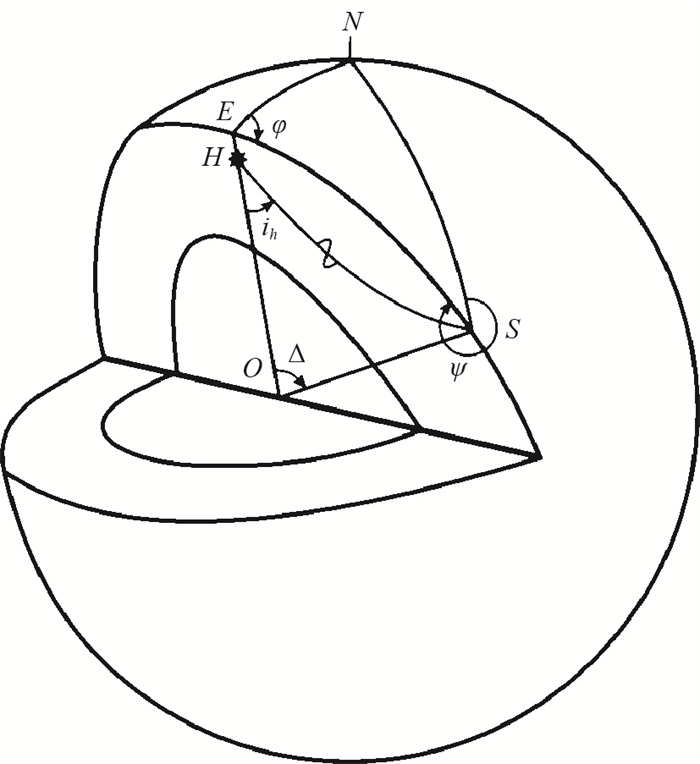
但是,由射线弯曲所引起的上述困难可以用下述办法克服. 图 4中的H表示一个震源深度为h的震源,S是台站,N是北极,φ是由震中E指向台站S的方位角,ψ是由台站指向震中的方位角(Ben-Menahem and Singh, 1981). 由图可见,如果把在S的观测结果逆着射线回溯到以H为球心、以充分小的长度为半径的、均匀的小球的球面上,就可以在小球球面上把理论分析和观测结果加以对比,从而克服由于地球不均匀性引起的困难. 这个理想化的、均匀的小球称为震源球(focal sphere)(图 5). 在震源球球面上,和台站S相对应的点P称为假想点(conventional point),对于下行射线,它的位置可以用射线离开震源时的方向与沿地球半径指向地心的方向的夹角ih和震中E指向台站S的方位角φ表示. ih称为离源角(take-off angle),0°≤ih≤90°. 对于上行射线,ih定义为射线离开震源H [在图 3(a)所示情形下也即震中E]时的方向与地球半径方向的夹角,0°≤ih≤90°. 在历史上(Byerly,1926;Кейлис-Борок,1957;Honda, 1957, 1961, 1962),曾经采用过与震源球概念本质上一样的、称为台站的延伸位置(extended position)的概念以克服由于射线弯曲所引起的困难.
|
图 4 离源角 Fig.4 Take-off angle |

|
图 5 震源球 Fig.5 Focal sphere |
如图 3(a)所示,以离源角ih离开震源的平直射线(straightened ray)、即假定地球是均匀球体时的地震射线ES′与地球球面的交点S′称为台站S的延伸位置. 对于如图 3(b)所示的震源深度为h的情形,平直射线HS′与剥去厚度为h的壳层之后的地球(“剥壳地球”)球面的交点S′称为台站S的延伸位置(Stauder,1962). 在球对称介质中,由斯涅耳(Snell)定律,可以得出地震射线遵从以下定律:
| $ \frac{{{r_h}\sin {i_h}}}{{{v_h}}} = \frac{{{r_0}\sin {i_0}}}{{{v_0}}}, $ | (1) |
式中,r0是地球半径,rh=r0 - h,其中v0和vh分别是地面处和震源所在深度h的地震波速度,i0是入射角. 入射角i0可由地震波的时距曲线t(Δ, h)求得:
| $ \sin {i_0} = {v_0}\frac{{{\rm{d}}t}}{{{\rm{d}}\Delta }}, $ | (2) |
式中,t = t(Δ, h)是地震波的走时,Δ是震中距,在这里,Δ以长度(例如km)为单位. 因此,作为震中距Δ和震源深度的函数的离源角ih = ih(Δ, h)可由下式求得:
| $ \sin {i_h} = \frac{{{r_0}}}{{{r_0} - h}}{v_h}\frac{{{\rm{d}}t}}{{{\rm{d}}\Delta }}. $ | (3) |
由地球半径r0,震源深度h,震源所在深度的地震波速度vh以及时距曲线t(Δ, h)的斜率,便可由式(3)计算出ih(∆, h)(Pho and Behe, 1972;Chandra,1972).
1.3 投影方法的应用 1.3.1 极射赤面投影.为了在平面上表示震源球,需要把它投影到某一平面上. 有许多种方法可以做到这点,其中常用的一种方法是极射赤面投影法(stereographic projection).
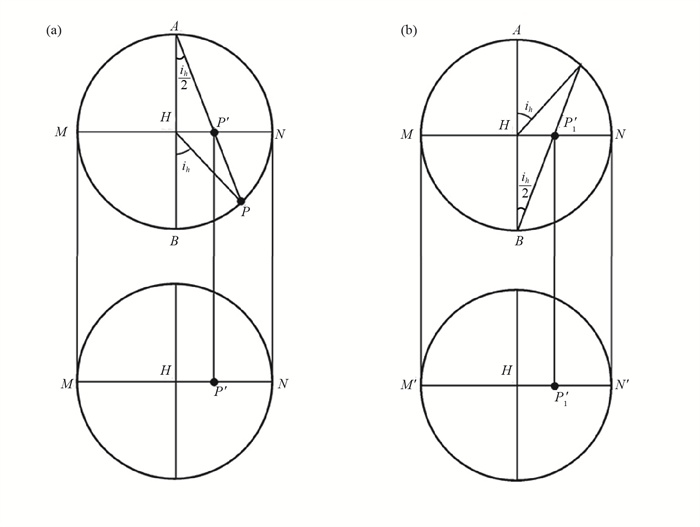
对于远震来说,射线离开震源朝下到达地震台,此时与台站S相应的假想点P在震源球下半球球面上. 我们可以按极射赤面投影原理把它投影到水平面上. 图 6(a)表示了极射赤面投影原理(下半球投影). 图 6(a)的上图表示一个过震源球球心H和假想点P的垂直平面,而下图则为赤道面(投影平面)的平面图,AB是这个面在H点的垂线,A和B分别是这条垂线与上半球和下半球球面的交点. AB称为极轴,A点与B点称为极. 连接PA交赤道面于P′点,P′点便称为下半球球面上的P点在赤道面上的投影. 设震源球半径为R,按照此投影方法,震源球下半球便投影到赤道面上半径也为R的圆内(Scheidegger,1957;Stauder,1962;Aki and Richards, 1980).
|
图 6 极射赤面投影 (a) 震源球下半球投影;(b) 震源球上半球投影 Fig.6 Stereographic progection (a) Lower hemispheric projection of focal sphere; (b) Upper hemispheric projection of focal sphere |
图 6(a)只表示出震源球下半球的极射赤面投影. 对于近震或地方震来说,射线离开震源朝上到达地震台. 此时,与台站S相应的假想点P1位于震源球上半球球面上[图 6(b)]. 设赤道面在H点的垂线与下半球球面交于B点. 连结P1B交赤道面于P′1点,P′1点便是上半球球面上的P1点在赤道面上的投影. 这样,震源球上半球便投影到半径也为R的圆内.
在极射赤面投影图上,P点的投影P′的位置由震中E指向台站S的方位角φ和P′与H的距离r确定,由图 6易得:
| $ r = R\tan (\frac{{{i_h}}}{2}). $ | (4) |
这样,P′的位置(φ, r)便可由(φ, ih)完全确定.
以各种不同角度跟赤道面斜交的平面(子午圈、经圈)在投影图中是一些圆弧,而与图 7中的平面平行的一系列平面(卯酉圈、纬圈)在投影图中是与上述圆弧正交的曲线簇[图 8(a)]. 这两组彼此正交的曲线簇构成乌尔夫网(Wulff net)(Kasahara,1981). 在实际应用中,利用乌尔夫网可以简便地在平面上确定出由(φ, ih)所表示的假想点P在投影图上的位置(φ, r)以及把初动符号隔开的两个彼此正交的平面的位置.
|
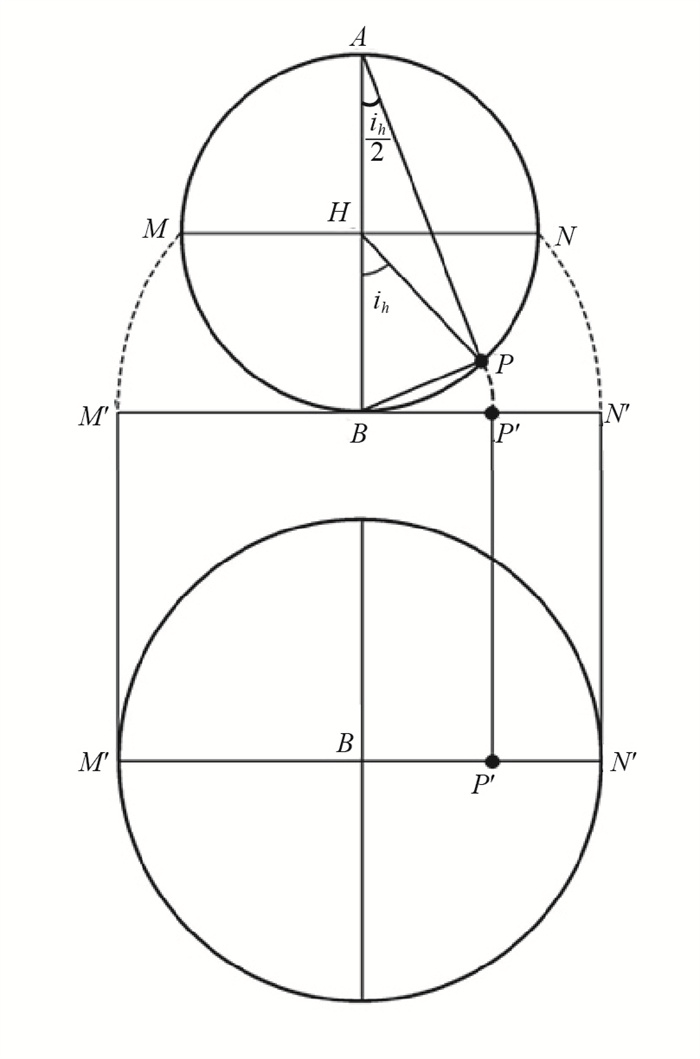
图 7 震源球下半球等面积投影 Fig.7 Lower hemispheric equal-area projection of focal sphere |
|
图 8 乌尔夫网(a)和斯密特网(b) Fig.8 Wulff net (a) and Schmidt net(b) |
极射赤面投影是一种保角变换:过P点的、夹角为α的两段圆弧元在赤道面上的投影是过其投影P′点的两段直线元,这两段直线元的夹角等于α. 过P′点的直线元与过P点的相应圆弧元的比值与方向无关,恒等于(1/2)sec2(ih/2). 所以在震源球球面上的P点的面积元经过投影后面积变成原面积的(1/4)sec4(ih/2)倍. 这说明,极射赤面投影相对地放大了离源角大的区域的面积;它相对地压缩了离源角小的区域的面积. 一般说来,实际观测资料中多数是离源角小于45°的假想点,采用极射赤面投影将会相对地缩小实际资料中多数资料点分布的区域. 因为这个缘故,用极射赤面投影方法(乌尔夫网)表示地震断层面解的人逐渐减少.
1.3.2 等面积投影.另一种经常采用的投影方法是天顶等面积投影法(zenithal equal-area projection),也称为施密特—兰伯特等面积投影法(Schmidt-Lambert equal-area projection),简称等面积投影法(equal-area projection).等面积投影法是按图 7所示的作图法,即取图中的BP'=BP,把震源球球面上的P点投影到在B点与下半球球面相切的平面上的P′点;投影时,方位角φ不变,而P′与B的距离r为
| $ r = 2R\sin (\frac{{{i_h}}}{2}). $ | (5) |
图 7的上图表示一个过震源球球心H和点P的垂直平面,下图为投影面的平面图. 容易看出,震源球下半球的投影是半径为
在P点的面积元R2sinihdihdφ经过投影,变成在P′点的面积元,且投影前后面积元的面积相等,即
| $ 2R\sin (\frac{{{i_h}}}{2}){\rm{d}}\varphi \frac{{\rm{d}}}{{{\rm{d}}{i_h}}}[2R\sin (\frac{{{i_h}}}{2})]{\rm{d}}{i_h} = {R^2}\sin {i_h}{\rm{d}}{i_h}{\rm{d}}\varphi, $ | (6) |
也即,在震源球球面上原先面积相等的两个面积元经投影后面积仍相等,所以称这种投影为等面积投影. 与极射赤面投影不同,等面积投影并不保角,在震源球球面上过一点的两段圆弧元的夹角,投影后其夹角的正切按cos2(ih/2)的比例变化. 随着ih的增大,角度的畸变愈来愈大,特别是当假想点P在上半球时. 为避免这一缺点,可将上半球和下半球分别投影. 此时,每半个震源球(面积均为2πR2)投影后均变成面积为2πR2的圆.
与极射赤面投影做法类似,按等面积投影原理,可把一系列经圈和纬圈投影到赤道面上,由此得到的两组曲线簇构成如图 8(b)所示的施密特网(Schmidt net)(Kasahara,1981).
由于等面积投影具有保持面积元的面积不变从而台站的假想点相对分布不发生畸变的优点,并且如果上、下半个震源球分别投影,又具有角度畸变小的优点,所以等面积投影现在越来越多地被用于表示地震的断层面解.
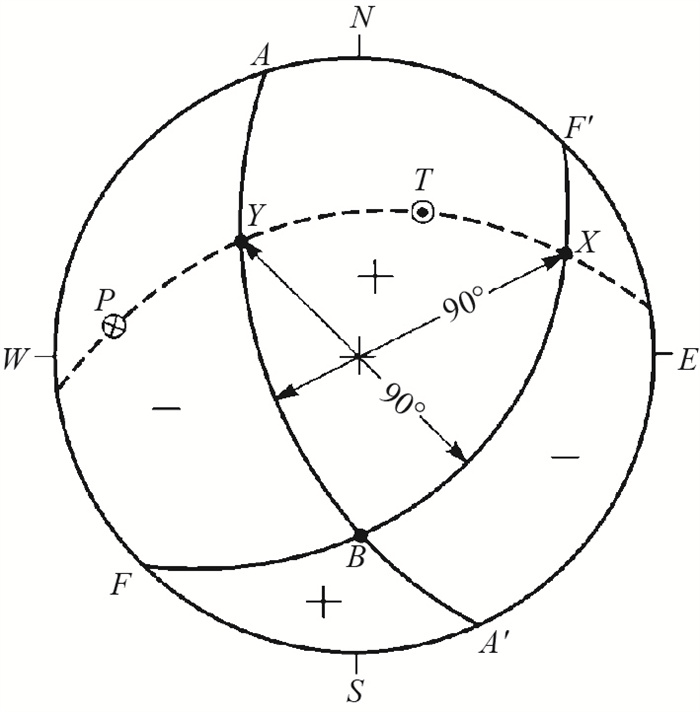
把纵波初动符号交替地分开的两个节平面在投影图里是两段圆弧. 断层面FF′和辅助面AA′是彼此正交的两个平面,所以在投影图上,断层面FF′的极Y位于辅助面AA′上;AA′的极X位于FF′上(图 9).

|
图 9 正交条件 Fig.9 Orthogonal condition |
这种情况称为正交条件. 所得到的地震的断层面和与它垂直的辅助面的参量及其他有关的参量称为地震的断层面解(fault-plane solution),也称为地震的震源机制解(focal mechanism solution).
1.3.3 其他投影方法.如前已述,利用P波初动的压缩与膨胀的分布研究地震的震源机制是最早采用来研究地震震源机制的方法. 由于这个方法所使用的资料仅仅是P波初动资料,比较简单易行,结果稳定可靠,所以至今仍在广泛使用.
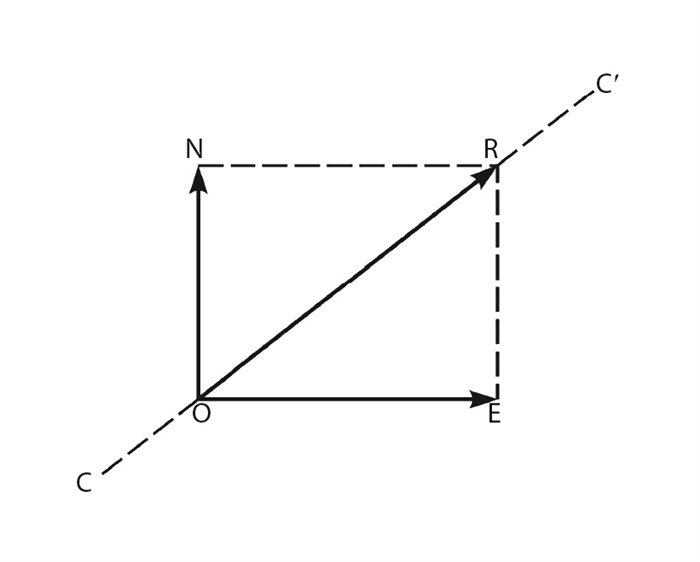
在地震台上记录到的地震P波的初动方向有时是压缩、有时是膨胀,在地震学历史上是一件早已被注意到的观测事实. 1909年,俄国的一位王子、物理学家伽里津(Гaлицын,Борис Б.,1862—1916)第一个肯定地指出了这一观测事实(Galitzin,1909;Гaлицын,1912). 他根据在地震仪上记录到的地动南—北与东—西分量构制矢量图,在确定震中时运用了这一观测事实(图 10). 合矢量(图 10中的OR)位于包含震中C和台站O的大圆CC′中. 如果在垂直向地震仪上记录到的初动是朝上,则初动是压缩[图 2(a)],合运动背离震源,因此可判定震源位于C方向;如果初动是朝下,则初动是膨胀,合运动指向震源,因此可判定震源位于C′方向[图 2(b)]. 后来,虽然有一些地震学家注意到同一地区的地震在同一地震台上总是产生同一类型的初动,即或者是压缩,或者是膨胀;特别是在地震台网密集的日本以及欧洲的某些地区,地震学家也注意到同一地震在某一地区的许多地震台上记录到的P波初动是压缩,而在另一地区的许多地震台上记到的P波初动则是膨胀. 但是最先注意到P波初动的压缩与膨胀的分布可能与地震机制有关联的则是地震学家Walker(1913). 根据河角广(Kawasumi,Hiroshi,1904—1972)的研究(Kawasumi,1937)的研究,日本的志田顺(Shida,Toshi,1876—1936)最先确立P波初动的压缩与膨胀的四象限分布.
|
图 10 确定震中方向的伽里津Galitgin’s(Гaлицын)方法 Fig.10 Galitgin's method for determining the direction of an earthquake epicenter |
震源机制研究的近代发展始于1926年. 拜尔利(Byerly,Perry,1897—1978)在研究1925年发生于美国蒙塔那(Montana)州的一次地震时,在地震学历史上第一次把分布于全球的许多地震台记录的单个地震的P波初动方向用表格列出(Byerly,1926). 拜尔利当时曾试图进一步划分出P波初动是压缩或膨胀的扇形区域,但没有能够据此进一步探讨震源的性质,部分原因是他对一个关键的地震台上的P波初动方向有怀疑. 两年以后,拜尔利(Byerly,1928)对1922年发生于智利的一次地震做了类似的研究. 他接受了雷德(Reid,Harry Fielding,1859—1944)的弹性回跳理论(Reid, 1910, 1911),运用了中野广(Nakano,Hiroshi,1894—1929)的理论结果(Nakano,1923),设想产生这样的P波初动分布的地震震源是一个脉冲地作用于震源处的单力. 过了一年,他增添了智利地震的勒夫(Love)波资料,重新分析研究了这个问题(Byerly,1930). 这回他设想震源是一对平行于断层作用的单力偶. 在以后10年左右的时间里,拜尔利继续研究该问题,逐渐完善了被地震学家称之为确定断层面解的拜尔利方法(Byerly, 1938, 1955;De Bremaecker,1956). 拜尔利发现,如果我们能够求得围绕震源区域的P波初动方向,便能推出断层的取向与在断层上的运动方向. 但这面临两个困难:第一,地球介质是不均匀的,这点与中野广(Nakano,1923)的理论结果所依据的均匀介质的假设不符;第二,难以从观测资料确定两个未知的正交的平面与球面的交线. 为了克服这两个困难,拜尔利做出了两个意义重大的贡献:第一,他提出了台站的延伸位置的概念;第二,他运用了极射赤面投影方法.
图 11(a)表示了拜尔利所提出并采用的台站的延伸位置概念与极射赤面投影方法. 图中圆圈表示地球,C表示地心,E表示位于地球表面的震源,S为地震台,ES′是平直射线,ih是离源角,S′是台站S的延伸位置. 拜尔利以震中的对蹠点(anticenter)E′为投影点,连结E′与S′,E′S′的延长线与以EE′为极轴的赤道面的交点S″,便是S′在赤道面上的投影. 按照拜尔利所采用的方法,通过ES′垂直于纸面(垂直截面)的平面与地球表面相交截出的圆的投影是水平截面上直径为CS′的圆.

|
图 11 各种投影方法之比较 (a) 拜尔利(Byerly)所提出并采用的台站延伸位置概念与极射赤面投影方法;(b) 诺波夫(Knopoff)所采用的台站延伸位置概念与中心投影方法;(c) 斯陶德尔(Stauder)所采用的震源球概念与中心投影方法;(d) 震源球概念与极射赤面投影;(e) 震源球概念与等面积投影;(f) 本多弘吉(Honda) 所采用的机制图 Fig.11 Comparison of different projection methods (a) The concept of station extended position and stereographic projection method proposed and used by Byerly; (b) The concept of station extended position and central projection method used by Knopoff; (c) The concept of focal sphere and central projection method use by Stauder; (d) The concept of focal sphere and stereographic projection; (e) The concept of focal sphere and equal area projection; (f) The mechanism diagram used by Honda |
诺波夫(Knopoff,Leon,1925—2011)采用了与拜尔利相同的台站延伸位置的概念但不同的投影方法——中心投影方法[图 11(b)](Knopoff,1961). 在图 11(b)中,将台站的延伸位置S′与E的连线ES'的延长线与过E′平行于赤道面的平面的交点S″,便是S′以E点为投影点的中心投影. 通过ES'垂直于纸面(垂直截面)的平面,经上述中心投影后是水平截面上过E′的纵轴与过S″平行于纵轴的直线之间的条带.
斯陶徳尔(Stauder,William S. J.,1922—2002)采用了震源球的概念与以震源H为投影点的中心投影方法[图 11(c)]. 若按斯陶徳尔采用的中心投影方法,通过HP垂直于纸面(垂直截面)的平面经中心投影后,是水平截面上过B的纵轴与过P′平行于纵轴的直线之间的条带(Stauder,1962).
以本多弘吉(Honda,Hirokichi,1906—1982)为代表的日本地震学家早期的工作与西方地震学家不同. 他们依托日本密集的地震台网,不用投影法求节平面,而是在地图上标出P波初动符号,直接画出节线. 这种做法的缺点是,容易夸大节平面的倾角,因为只有搜集、运用全球范围的资料,才能较准确地确定三维空间中的节平面.
尽管日本地震学家早期的工作是在地图上直接作图,没有使用投影方法确定断层面,但却率先采用了把节线投影到他们称为模型球(model sphere)、现在称为震源球的方法(Honda, 1957, 1962). 如图 11(f)所示,P点表示节线上的一个点,P′是它在过A点的、平行于赤道面的水平面上的垂直投影. 由通过HP垂直于纸面(垂直截面)的平面,经上述垂直投影,得到如图 11(f)下图所示的阴影区. 本多弘吉称以这种投影方法表示的震源机制解称为机制图(mechanism diagram).
作为比较,图 11(d,e)分别给出了前面已述及的极射赤面投影[图 6(a)]和等面积投影[图 6(b)]. 与图 6(b)所示的等面积投影法的做法不同,在图 11(e)所示的等面积投影中,由H向AP引垂线HP'. 显然,HP'=BP/2. 在投影时,方位角φ不变,而取通过H的赤道面上的HP'1=HP,便把震源球球面上的P点投影到通过H的赤道面上的P'1点. 此时,P'1与H的距离HP'1=Rsin(ih/2) = r/2[参见式(5)]. 显然,图 11(e)所示的等面积投影的定义,与图 6(b)所示的定义并无本质差别.
1.3.4 各种方法的等效性.日本地震学家在震源机制方面的工作是独立于其他国家的地震学家进行的. 中野广(Nakano,1923)关于地震震源机制的理论文章是根据Walker(1913)书中的一个建议写成的. 他的这篇关于地震震源机制的重要论文发表于1923年,但不幸的是,这篇论文毁于1923年9月1日东京大地震引发的大火灾,只有极少量侥幸流入欧美、澳、新西兰得以倖免. 中野广在东京大地震后不久(1929年)即逝世. 一个偶然的机会,他的学生本多弘吉发现了中野广为撰写该论文而草拟的提纲,他根据自己的记忆和理解,为该手稿补写了公式推导并将其发表(Honda,1938). 在松泽武雄(Matsuzawa,Takeo,1902—1989)的论文(Matsuzawa, 1926, 1964)和中野广的后续论文以及妹泽克惟(Sezawa,Katsutada,1895—1944)的著作(Sezawa, 1932, 1935)中,对中野广(Nakano, 1923, 1930)的方法均有简要叙述. 与此同时,中村森太郎(Nakamura,Saemon-Taro,1891—1974)、和达清夫(Wadati,Kiyoo,1902—1995)、石本巳四雄(Ishimoto,Mishio,1893—1940)等对节平面的观测与解释均有所贡献(Nakamura,1922). 20世纪30年代后,本多弘吉(Honda, 1931, 1954, 1957, 1962;Honda and Masatsuka, 1952;Honda and Emura, 1958)是日本在这一领域的主要科学家,他在理论与观测方面均做出重要贡献. 日本地震学家最重要的贡献便是“模型球”即震源球概念的提出和投影方法“机制图”的运用(Honda and Emura, 1958).
荷兰地震学家的工作开始于20世纪30年代,也是独立于美国与日本的地震学家的工作进行的. Koning(1942)最先注意到了震源球概念的运用,并且第一个在震源机制研究中运用了乌尔夫网. 我们现在是用乌尔夫网作震源球的投影,而Koning当初则是用乌尔夫网作地球自身表面的投影. Ritsema(1955,1957,1958a,b,1959)则在Koning(1942)早期工作的基础上,极大地发展与完善了Koning的工作. 他是第一个采用震源球概念与震源球极射赤面投影方法(乌尔夫网)完整地确定地震断层面解的地震学家. 为便利于把资料画在乌尔夫网上的工作,Ritsema计算了许多种波的各种震源深度的离源角ih(Δ, h)曲线.此外,Ritsema还把他的方法推广应用于S波资料(Ritsema and Veldkamp, 1960).
以克依利斯-博洛克(Кейлис-Борок,Владимир И.,1921—2013)与维京斯卡娅(Введенскя,Анна Викторовна,1923—1997)为代表的苏联地震学家在震源机制方面的工作始于1948年(Введенскя,1956;Кейлис-Борок,1957;Keylis-Borok, 1957, 1959, 1961;Balakina et al,1961a, b;Keylis-Borok et al,1972). 1948年10月5日土库曼阿什哈巴德MS 7.3地震的发生推动了苏联在第二次世界大战后地震研究的发展. 1950年代中期以后,他们开始采用震源球的极射赤面投影方法(乌尔夫网)来表示地震体波初动的极性. 与美、日、荷等国家的地震学家的工作不同,苏联地震学家先是研究近震的机制,而后再扩展至远震. Кейлис-Борок(1957)的方法与Byerly(1928),Koning(1942)、Ritsema(1955)等的方法类似,但有两点不同(Keylis-Borok, 1957, 1959, 1961;Кейлис-Борок,1957;Balakina et al,1961a, b). 第一,拜尔利只用了P波初动方向的信息,而克依利斯-博洛克等则试图最大限度地利用地震图中的信息,例如P,SV和SH波初动的极性及其节面、S波与P波的振幅比,SH波与SV波的振幅比. 第二,他们比其他国家的地震学家更全面地研究了点源理论及多层介质与倾斜界面的影响. 尽管这些研究结果在常规的分析工作中不常得到应用,但却有助于深化对所使用的方法本身及其局限性的理解. 与Byerly(1928)所采用的台站的延伸位置概念类似,克依利斯-博洛克采用的是平直射线与假想点的概念(Кейлис-Борок,1957). 克依利斯-博洛克也用乌尔夫网. 可能是因为研究近震的缘故,他们采用的是震源球上半球的投影(Кейлис-Борок,1957).
由于战争(第二次世界大战)、语言文字(美、日、荷、俄)以及表示方法与投影方法不同形成的壁垒,上述4个国家科学家的研究工作几乎是互不通气地独立发展的.直至1957年,Scheidegger(1957)经过透彻的分析对比研究后指出,上述几种方法本质上是一样的,都是运用初动的观测资料求节面的位置,然后由节面推出震源处的运动方向或力的方向;他们的差别仅在于表示方法与投影方法的不同. Scheidegger(1957)不仅指出了美、日、荷、苏地震学家的震源机制研究本质上是等效的,而且促使各国地震学家关注其他国家同行专家的工作,增进了相互了解. 而在Scheidegger(1957)发表这篇论文之前,由于上述原因,这些国家的地震学家彼此缺乏交流,互不了解. 他的论文对增进各国同行专家的相互了解做出了重大贡献,从而成为了震源机制研究的一个转折点. 震源机制研究从此进入了一个蓬勃发展的时期(Hodgson,1957;Nuttli,1958;Kasahara, 1958, 1981;Scheidegger,1958;Stauder, 1960a, b, c,1962;Stauder and Adams, 1961;Ingram,1961;Scholte,1962;Scholte and Ritsema, 1962;Stauder 1964;1966;Chandra,1971;Dillinger et al., 1972;Khattri,1973).
Aki K and Richards P G. Quantitative Seismology: Theory and Methods, 1 & 2[M]. San Francisco: W. H. Freeman, 1980: 1-932.
|
安艺敬一, P. G. 理查兹. 定量地震学. 第1, 2卷[M]. 李钦祖, 邹其嘉, 等译. 北京: 地震出版社, 1986: 1-620, 1-406.
|
Balakina L M, Savarensky E F, Vvedenskaya A V. On determination of earthquake mechanism[J]. In: Ahrens L M et al. (eds.). Physics and Chemistry of the Earth, 1961a, 4: 211-238. |
Balakina L M, Shirokova H I, Vvedenskaya A V. Study of stresses and ruptures in earthquake foci with the aid of dislocation theory[J]. Publ Dom Obs Ottawa, 1961b, 24: 321-327. |
Ben-Menahem A, Singh S J. Seismic Waves and Sources[M]. New York: Springer-Verlag, 1981: 1-1 108.
|
Bormann P (ed.).. IASPEI New Manual of Seismological Observatory Practice. 1 & 2[M]. Potsdam: GeoForschungs Zentrum Potsdam, 2002: 1-737, 738-1109.
|
Brumbaugh D S. Classical focal mechanism techniques for body waves[J]. Geological Surveys, 1979, 3: 297-329. |
Bullen K E, Bolt B A. An Introduction to the Theory of Seismology[M]. 4th edition. Cambridge: Cambridge University Press, 1985: 1-500.
|
K E布伦, B A博尔特著. 地震学引论[M]. 李钦祖, 邹其嘉译校. 北京: 地震出版社, 1988: 1-543.
|
Byerly P. The nature of the first motion in the Chilean earthquake of November 11, 1922[J]. Am J Sci, 1928, 16: 232-236. |
Byerly P. Nature of faulting as deduced from seismograms[J]. Crust of the Earth, Geol Soc Am Sp Paper, 1955, 62: 75-85. |
Byerly P. The earthquake of July 6, 1934:Amplitudes and first motion[J]. Bull Seismol Soc Am, 1938, 28: 1-22. DOI:10.1785/BSSA0280010001 |
Byerly P. The Montana earthquake of June 28, 1925[J]. Bull Seismol Soc Am, 1926, 16: 209-263. DOI:10.1785/BSSA0160040209 |
Byerly P. Love waves and the nature of the motion at the origin of the Chilean earthquake of November 11, 1922[J]. Am J Sci, 1930, 19: 274-282. |
Chandra U. Angles of incidence of S-waves[J]. Bull Seismol Soc Am, 1972, 62: 903-915. DOI:10.1785/BSSA0620040903 |
Chandra U. Combination of P and S data for the determination of earthquake focal mechanism[J]. Bull Seismol Soc Am, 1971, 61: 1655-1673. DOI:10.1785/BSSA0610061655 |
De Bremaecker J Cl. Remark on Byerly's fault-plane method[J]. Bull Seismol Soc Am, 1956, 46: 215-216. DOI:10.1785/BSSA0460030215 |
Dillinger W H, Harding S T, Pope A J. Determining maximum likehood body wave focal plane solutions[J]. Geophys J R astr Soc, 1972, 30: 315-329. DOI:10.1111/j.1365-246X.1972.tb05817.x |
Galitzin B B. Zur Frage der Bestimmung des Azimuts des Epizentruns eines Bebens[R]. Assoc, Intern de Seismologie, 1909: 132-141.
|
Herrmann R B. A student's guide to the use of P and S wave data for focal mechanism determination[J]. Earthquake Notes, 1975, 46: 29-39. |
Hodgson J H. Nature of faulting in large earthquakes[J]. Bull Geol Soc Am, 1957, 68: 1611-1643. |
Honda H, Emura K. Some charts for studying the mechanism of earthquakes[J]. Sci Repts Tohoku Univ, Ser.5, Geophys, 1958, Suppl. 9: 113-119. |
Honda H, Masatsuka A. On the mechanisms of the earthquakes and the stresses producing them in Japan and its vicinity[J]. Sci. Repts Tohoku Univ, Ser. 5, Geophys, 1952, 4: 42-59. |
Honda H. Earthquake mechanism and seismic waves[J]. J Phys. Earth, 1962, 10(suppl): 1-98. |
Honda H. On the initial motion and the types of the seismograms of the north Idu and the Ito earthquakes[J]. Geophys Mag, 1931, 4: 185-213. |
Honda H. The generation of seismic waves[M]. Pub Dominion Obs Ottawa, 24, 1961: 329-334.
|
Honda H. The Late Dr Nakano's manuscript on generation of seismic waves[J]. Kenshin Ziho, 1938, 10: 315-326. |
Honda H. The mechanism of the earthquakes[J]. Sci Repts Tohoku Univ, Ser. 9, Geophys (Suppl.): 1-46. Pub. Dominion Obs. Ottawa. 20,, 1957, 295-340. |
Honda H. The Seismic Waves[M]. 1954: 1-230. (in Japanese)
|
Ingram R E S J. Generalized focal mechanism[M]. Publ Dom Obs Ottawa 24, 1961: 305-308.
|
Kasahara K. Earthquake Mechanics[M]. Cambridge: Cambridge University Press, 1981: 1-261.
|
笠原庆一. 地震力学[M]. 赵仲和译. 北京: 地震出版社, 1986: 1-248.
|
Kasahara K. The nature of seismic origins[J]. Bull Earthquake Res Inst, 1958, 36: 21-33. |
Kawasumi H. A historical sketch of the development of knowledge concerning the initial motion of an earthquake[J]. Publ. Bur. Cent Sismol Int, Ser. A, Trav Sci, 1937, 15: 1-76. |
Keylis-Borok V I, Pistetkiik-Shapiroi I, Pisarenko V F, Zhelan Kuia T S. Computer determination of earthquake mechanism. In: Keylis-Borok V I (ed.). Computational Seismology[M]. New York: Plenum Pub Co, 1972: 32-45.
|
Keylis-Borok V I. Some new investigations of earthquake mechanisms[M]. Pub Dominion Obs Ottawa 24, 1961: 335-341.
|
Keylis-Borok V I. The determination of earthquake mechanisms using both longitudinal and transverse waves[J]. Ann di Geofis, 1957, 10: 105-128. |
Keylis-Borok V I. The study of earthquake mechanisms[M]. Pub Dominion Obs Ottawa 20, 1959: 279-294.
|
Khattri K. Earthquake focal mechanism studies-A review[J]. Earth Sci. Rev, 1973, 9: 19-63. DOI:10.1016/0012-8252(73)90161-X |
Knopoff L. Analytical calculation of the fault plane problem[M]. Publ Dom Obs Ottawa 24, 1961: 309-315.
|
Koning L P G. On the mechanism of deep-focus earthquakes[J]. Gerl Beitr Geophys, 1942, 58: 159-197. |
Matsuzawa T. On the relative magnitude of the preliminary and principal portion of an earthquake[J]. Jap J Ast Geophys, 1926, 4: 1-23. |
Matuzawa T. Study of Earthquakes[M]. Tokyo: Uno Shoten, 1964: 1-213.
|
Nakamura S. On the direction of the first movement of the earthquake[J]. J Meteorol Soc Japan, 1922, 41(2): 1-10. DOI:10.2151/jmsj1882.41.2_en1 |
Nakano H. Notes on the nature of the forces which give rise to the earthquake motions[J]. Seismol Bull, Central Meteor Obs Japan, 1923, 1: 92-120. |
Nakano H. Some problems concerning the propagation of the disturbances in and on a semi-infinite elastic solid[J]. Geophys, 1930, Mag, 2: 189-348. |
Nuttli O. A method, using S wave data, of determining the direction of horizontal forces which produce an earthquake[J]. Earthquake Notes, 1958, 29: 12-14. |
Pho H-T, Behe L. Extended distances and angles of incidence of P waves[J]. Bull Seismol Soc Am, 1972, 62: 885-902. |
Reid H F. The elastic-rebound theory of earthquakes[J]. Univ Calif Bull Dep Geol Sci, 1911, 6: 413-444. |
Reid H F. The Mechanism of the Earthquake. In: Andrew C. Lawson (Chairman), Report of the State Earthquake Investigation Commission[R]. Publication 87, The California Earthquake of April 18, 1906. Vol. 2. Washington, DC: Carnegie Institution of Washington, 1910: 1-192.
|
Ritsema A R, Veldkamp J. Fault plane mechanisms of southeast Asian earthquakes[J]. Mededelingen en Verhand. Koninklijk Nederlands Meteorologisch Institut, 1960, 76: 7-63. |
Ritsema A R. (ih, Δ) curves for bodily seismic waves of any focal depth[J]. Verhand Meteorol Geofisik Inst (Djakarta), 1958b, No.54. |
Ritsema A R. On the focal mechanism of southeast Asian earthquakes[M]. Publ Dom Obs, Ottawa 20, 1959: 341-368.
|
Ritsema A R. On the use of transverse waves in earthquake mechanism studies[J]. Verhand Meteorol Geofisk Inst (Djakarta),, 1957, No.52. |
Ritsema A R. Over diepe Aarabevingen in de Indische Archipelago[D]. Dissertation, Utrecht Univ, Netherlands, 1958a.
|
Ritsema A R. The fault technique and the mechanism in the focus of the Hindo-Kush earthquakes[J]. Indian J Metero Geophys, 1955, 6: 41-50. |
Scheidegger A E. On the fault plane solution of earthquakes[J]. Geofis Pura Appl, 1958, 39: 13-18. DOI:10.1007/BF02001128 |
Scheidegger A E. The geometrical representation of fault plane solutions of earthquakes[J]. Bull Seismol Soc Am, 1957, 47: 89-110. DOI:10.1785/BSSA0470020089 |
Scholte J G J, Ritsema A R. Generation of earthquake by a volume source with moment[J]. Bull Seismol Soc Am, 1962, 52: 747-765. DOI:10.1785/BSSA0520040747 |
Scholte J G J. The mechanism at the focus of an earthquake[J]. Bull Seismol Soc Am, 1962, 5: 711-721. |
Sezawa K. Amplitude of P and S waves at different focal distances[J]. Bull Earthq Res Inst, 1932, 10: 299-334. |
Sezawa K. Elastic waves produced by applying statical force to a body or by releasing it from a body[J]. Bull Earthq Res Inst, 1935, 13: 740-749. |
Stauder S J W, Adams W M. A comparison of some S-wave studies of earthquake mechanisms[J]. Bull Seismol Soc Am, 1961, 51: 277-292. DOI:10.1785/BSSA0510020277 |
Stauder S J W, Bollinger G A. The S wave project for focal mechanism studies: Earthquakes of 1962[J]. Bull Seismol Soc Am, 1964, 54: 2199-2208. DOI:10.1785/BSSA05406B2199 |
Stauder S J W. S waves and focal mechanisms: the state of the question[J]. Bull Seismol Soc Am, 1960a, 50: 333-356. |
Stauder S J W. Three Kamchatka earthquakes[J]. Bull Seismol Soc Am, 1960b, 50: 347-388. DOI:10.1785/BSSA0500030347 |
Stauder S J W. S-waves: Alaska and other earthquakes[J]. Bull Seismol Soc Am, 1960c, 50: 581-597. DOI:10.1785/BSSA0500040581 |
Stauder S J W. The focal mechanism of earthquakes. In: Landsberg H E and Mieghem J V (eds.). Advances in Geophysics, 9[M]. New York: Academic Press, 1962: 1-76.
|
Udias A. Source mechanism of earthquakes[J]. Adv Geophys, 1991, 33: 81-140. |
Udias A, Madariaga R, Buforn E. Soure Mechanisms of Earthquakes. Theory and Practice[M]. Cambridge: Cambridge University Press, 2014: 1-302.
|
Walker G W. Modern Seismology[M]. London: Longmans, Green and Co, 1913: 1-88.
|
Введенская А В. Определение полей смещений при землетрясениях с помощью теории дислокцй[J]. Изв АН СССР, сер. Геофиз, 1956(3): 277-284. |
Галицын Б Б. Работы по сейсмология. Б. Б. Галицын Избранные Труды, 1912, Том 2: 231-465. Москва: Издательство Академии Наук СССР, 1960.
|
Кейлис-Борок В И. Исследование Механизма Землетрясений[M]. Тр. Геофиз. Ин-та АН СССР 40 (166), 1957. Москва: Изд. АН СССР. В. И.
|
彼徳·鲍曼主编. 新地震观测实践手册. 第1, 2卷[M]. 中国地震局监测预报司译, 金严, 陈培善, 许忠淮, 等校. 北京: 地震出版社, 2006: 1-572, 573-1 003.
|
克依利斯-博洛克. 地震机制的研究[M]. 李宗元译, 傅承义校, 北京: 科学出版社, 1961.
|
 2021, Vol. 42
2021, Vol. 42
