震级是地震时、空、强三要素之一,无论是在科学角度,还是社会需求角度,衡量地震的大小均是一件意义重大的基础性工作(傅承义等,1985;陈运泰等,2004;刘瑞丰等,2015)。精确的震级是进行地震预报、会商分析及科学研究的基础。当有感地震发生,特别是破坏性地震发生后,及时提供准确的地震参数,对应急救援工作的顺利开展至关重要。
单个地震台站所测定地震的震级大小与省级测震台网中心普遍存在差异,主要原因如下:①量取的S波位置及周期大小可能受经验影响,存在人为误差,需按规范操作;②地震波传播路径不同,可能影响振幅量取,从而影响震级测定;③观测仪器存在误差,如仪器灵敏度、仪器响应发生变化,将导致记录幅度存在差异;④台基影响。
关于震级偏差研究的文献较多,如:陈培善等(1983)分析震级偏差存在的原因;严尊国等(1992)、林仙坎(2006)、张志斌等(2018)、康清清等(2019)研究量规函数;刘阳等(2010)、郭延杰等(2020)研究台站方位角;戴维乐(1986)、曹复旺等(1988)、梁向军等(2019)分析近震震级偏差,等等。当涂地震站2015年10月投入地震观测,运行几年后发现,台站测出的震级(下文简称ML台)较安徽省测震台网中心所测震级(下文简称ML省)有一定偏差,本文主要分析震中距和方位角对震级偏差产生的影响。
1 台站概况马鞍山市当涂地震站(下文简称当涂站)位于安徽省马鞍山市当涂县大青山李白文化旅游区詹村,地理位置上在长江南岸。地质构造属下扬子断块,位于郯庐断裂带东侧,地貌为丘陵地形,台基为中生代花岗岩。
当涂站于2015年10月完成设备安装和调试,投入试运行。配备BBVS-60宽频带地震计和EDAS-24GN数据采集器进行数据记录和采集,利用交流供电,并配备UPS辅助电源,采用光纤网络,将数据传输至马鞍山市地震局监测中心和安徽省地震局台网中心。该台站硬件设施较好,供电和网络正常,观测数据连续率达99.9%,质量较高。
2 资料选取当涂站建站(2015年12月)以来至2020年4月,记录到1.2<ML<5.3近震120个(均采用ML震级标度表示),其中所选省外地震震级ML≥2.0,地震分布见图 1。所选地震均为浅源地震,具体参数见表 1(表中节选部分地震数据),其中1.2≤ML≤1.9地震8次,2.0≤ML≤2.9地震62次,3.0≤ML≤3.9地震40次,4.0≤ML≤4.9地震9次,5.0≤ML≤5.9地震1次。

|
图 1 所选地震震中分布 Fig.1 Epicenter distribution of selected earthquakes |
| 表 1 所选地震(部分)参数 Table 1 Parameters of selected earthquakes(part) |
影响地方性震级ML计算的主要因素有量规函数、台基效应和地震震源(地震波辐射方向)等(严尊国,1986),公式如下
| $ {M_{\rm{L}}} = \lg A + R\left(\mathit{\Delta } \right) $ | (1) |
| $ A = \frac{{{A_{\rm{N}}} + {A_{\rm{E}}}}}{2} $ | (2) |
式中,A为地动位移,单位μm;R(Δ)为量规函数;AN、AE分别为S波(或Lg波)NS向和EW向最大振幅,单位μm;Δ为震中距,单位km。
地震波的最大振幅应大于干扰水平2倍以上,需将S波(或Lg波)记录仿真成短周期地震仪(与省地震局仿真类型一致)NS、EW向水平记录后量取。为减少人为误差,振幅量取工作均由同一人严格按照要求完成。根据公式(1),计算得到当涂站记录的120个地震的单台震级ML台,与安徽省测震台网中心所测震级ML省进行对比,分析震级偏差C的变化规律,其中C = ML台 - ML省,具体数值见表 1(表中节选部分地震数据)。
3 震级偏差分析由于地壳构造的复杂性和不均匀性,地震波在地壳中的传播过程复杂,振幅也千变万化。同时,由于地震波辐射的方向性,台站方位不同,所测震级也会存在一定偏差(陈培善等,1983)。据震级计算公式(1),震级大小取决于两水平向的振幅和量规函数的大小。量规函数用来校准补偿地震波随距离的衰减,与震中距直接相关。震中距不同,最大振幅出现的地震波段也不同,一般:①Δ≤70 km,最大振幅出现在Sg波段;②70 km<Δ≤180 km,最大振幅出现在S11波段;③180 km<Δ≤300 km时,最大振幅出现在Sg震相之后数个周期;④Δ>300 km,最大振幅出现在Lg1或Lg2波段。
3.1 震中距对震级偏差的影响据陈培善等(1983)的分析,若量规函数正确,随着震中距的变化,震级偏差将在0值线上下摆动。
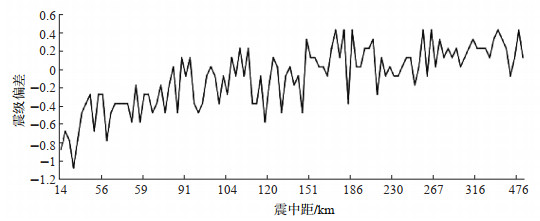
3.1.1 震中距的影响根据计算得到120个地震的震级偏差C,按照震中距大小进行排序,结果见图 2。
|
图 2 震级偏差随震中距大小的变化 Fig.2 Variation of magnitude deviation with epicenter distance |
(1)Δ<70 km,共分布18个地震,与ML省相比,单台震级ML台偏小,且震级偏差C随震中距增大而逐渐减小,最大达1.1,最小为0.2。量规函数描述了地震波随距离衰减的特性,与地壳构造紧密相关,具有明显的区域特征(薛志照,1992)。据严尊国等(1983)对我国西南及湖北省和闽台地区量规函数的研究,在震中距0—50 km范围内,地区不同,量规函数差异较大,而当涂站量规函数偏小,故所测单台震级偏小。
(2)70≤Δ≤180 km,共分布48个地震,且ML台大部分比ML省小,其中:C<0的地震有30个,偏差最小为-0.6;C>0的地震有11个,偏差最大为0.3,其他7个地震C = 0。在此震中距范围内,地震传播产生反射波。在该研究区内,震中距约70—120 km时,反射波最强,此范围内8个地震的震级偏差C≥0,其中7个地震的反射波较强,最大振幅位于反射波段。如:2018年4月6日23:55芜湖无为地震、2019年7月15日02:55常州溧阳地震,偏差C均为0.1,震中距分别为93 km、88 km(表 1),反映了莫霍面反射波的影响。Boore(2003)和Helmberger等(1993)也认为:震中距约100 km,强地面振动幅度不再随震中距增大而减小,其衰减关系曲线出现一段平坦,甚至共同增大现象,此现象可用莫霍面反射波SmS、sSmS等震相的传播机制来解释,表明当震中距达到反射波临界点,其振幅较强,甚至会与震中距一起增大,导致部分地震的单台震级偏大,以上2个震例与此一致。但是,受地震波射线路径和震源机制影响,部分地震即使震中距达到反射波临界点,其震级偏差却远小于0,如2016年4月15日14:49芜湖市无为地震,震中距94 km,其反射波虽强,但偏差C = -0.4(表 1)。
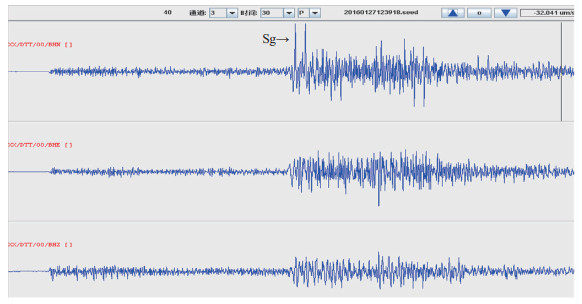
此外,由表 1可知,2016年1月27日12:39南京建邺地震,震中距为70 km,震级偏差C = 0,查看其波形图(图 3)发现:Sg波NS向振幅较大(箭头所指),远大于反射波振幅,Sg波EW向振幅比反射波振幅稍小,说明其震级偏大并不是因为反射波振幅大,仅仅是因为其横波振幅大。而同等震中距的其他地震(表 1)偏差值均远小于0。据陈培善等(1983)的分析,位于地震破裂不同方向的台站,如破裂前方和破裂后方,所测定震级可差0.3—0.5。据此分析,可知同等震中距的几次南京地震,与2016年1月27日12:39南京建邺地震的破裂方向不同,故当涂站所测震级偏差不同。陈培善等(1983)认为:在节线方向,S波辐射能量强,P波辐射能量为0,与节线成45°角,P波辐射较强,往往超过S波振幅,即所谓大头P波现象。建邺地震实际波形和震级偏差值与此论述一致。如2016年8月10日23:18南京浦口地震,震中距同为70 km,偏差C = -0.5,反射波较弱,P波较强,垂直向P波振幅与S波振幅差不多,而该震有“大头P波”现象,与震级偏小反映一致。
|
图 3 2016年1月27日12:39南京建邺地震波形 Fig.3 Seismic waveforms of Jianye, Nanjing, at 12:39 on Jan.27, 2016 |
(3)Δ>180 km,ML台普遍大于或等于ML省。此范围内共分布53个地震,只有8个地震的偏差C<0,其中六安地区的3个地震偏差绝对值较大(-0.4、-0.3、-0.2),其他5个地震偏差C均为-0.1;45个地震的偏差C≥0,差值均不超过0.4。因此,该段内量规函数大部分偏大。
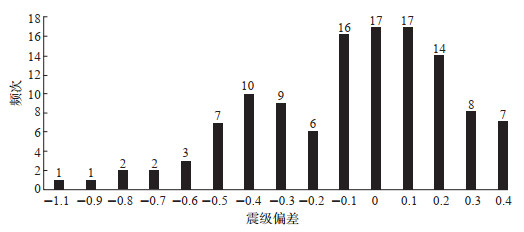
3.1.2 震级偏差频次分布按现有120个地震样本计算,当涂站震级平均偏差为-0.084,标准偏差为0.313 9,绘制地震震级偏差频次分布,结果见图 4。由图 4可见:①C<0时震级偏差分档较多;②C = 0和C = 0.1的地震最多;③震级偏差值的离散程度不高,且由于地震样本较少,震中分布也不密集、不均匀,导致震级偏差的频次分布并不完全遵循正态分布(图 4)。
|
图 4 震级偏差频次分布 Fig.4 Frequency distribution of magnitude deviation values |
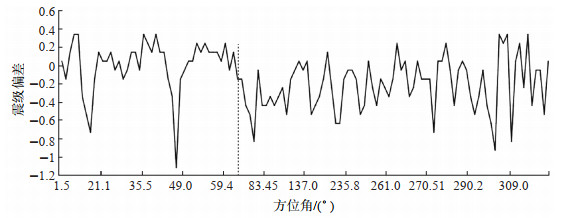
震级偏差也受地震波辐射方向的影响,而地震方位角则反映了地震波辐射的方向性。方位角是指:以台站为原点,台站正北与台站的连线和震中与台站连线的夹角(傅淑芳等,1980)。作者利用单台交互分析软件MSDP,量取所选地震的方位角,确保所得震中经纬度与省地震局所测接近。将120个地震的震级偏差按方位角进行分布,结果见图 5。
|
图 5 震级偏差随方位角大小的变化 Fig.5 Variation of magnitude deviation with azimuth |
由图 5可见:方位角约小于66°(图中虚线左侧),震级偏差大于0居多;方位角大于66°(图中虚线右侧),震级偏差小于0居多。据当涂站地理位置可知:①方位角小于66°的地震多分布在郯庐断裂带以东,也就是说,地震波未穿过郯庐断裂带和长江断裂破碎地带,能量损失较少。②方位角大于66°的地震多分布在郯庐断裂带以西,同时较多地震位于长江北岸,且只有少数地震方位角分布在90°—200°,大部分地震方位角在200°—360°,地震激发的部分能量被郯庐断裂和长江断裂破碎吸收,导致所测震级偏小。与戴维乐(1986)在对溧阳余震震级偏差随震中距变化的分析结果一致,即:穿过郯庐断裂带后,地震波能量消耗较多,震级偏小,震级偏差ΔM明显反向,呈负值分布。
3.3 震中距与方位角对震级偏差的综合影响笔者统计发现,在震源机制相同、震源深度相近的条件下,同一地区发生的地震震级偏差大多一致,一般同为正值或负值,统一偏大或偏小,较少存在偏差值正负号不一致现象。由于震级偏差在±0.2范围内是被允许的(傅淑芳等,1980),在此只关注震级偏差超过±0.2的地震。剔除其中震中距400 km以上的地震(地震数量少,不做统计),将发生在同一地区,震中距相近、方位角相近的地震,按方位角顺序进行震级偏差统计,结果见表 2。
| 表 2 震级偏差按方位角统计(取│C│>0.2) Table 2 Statistics of magnitude deviations by azimuth (│C│ > 0.2) |
由表 2可见:对于震中距和方位角相近的同一地区发生的地震,震级偏差存在2个共同点,即偏差方向相同(偏大或偏小),且数值相差较小。下面对表 2分类一一分析。
(1)震级偏差受量规函数的影响。马鞍山当涂站周边地区,如当涂、花山、江宁、博望、溧水、芜湖弋江、繁昌、和县、南京浦口,震中距均小于70 km,偏差均为负值。发生在以上地区的地震分布在当涂站东南西北方向,震级均偏小,说明在此震中距范围内,量规函数偏小。淮安盱眙、淮阴、盐城地区、黄海海域地震,震级偏大0.3—0.4,按前文所述,震中距大于180 km的地震震级普遍偏大,与此震中距范围的量规函数偏大有直接关系。
(2)震级偏差受断裂带和反射波的影响。芜湖繁昌的2次地震,震中距分别为59 km和71 km,所测震级均偏小0.6,与其他震中距相近的地震相比,震级偏小更多。分析认为,除与量规函数偏小有关外,还可能与地震射线穿过六合—马鞍山断裂(由芜湖市繁昌县经马鞍山市、南京市到南京市六合区)有关。同理,芜湖南陵地震震中距虽然在反射波临界范围内,但震级偏小较大,可能也与地震射线穿过南陵—小丹阳断裂(由芜湖市南陵县延伸至马鞍山到南京小丹阳)有关。芜湖无为县发生的3个地震(方位角在254.36°—261.0°)震中距均达到反射波临界点,反射波较强,测定震级偏小0.3—0.4。由于无为县位于长江北岸岸边,与当涂站隔江相望,地震波穿过长江断裂破碎带,部分能量被吸收,所以震级偏小。同理,铜陵枞阳也在长江北岸,震级偏差也较大(-0.5)。
另外,由表 1可知,无为县2018年4月6日23:55发生的地震(方位角为265.5°),其反射波P11和S11均较强,震级偏大0.1。4次无为县地震的震中距相近,但震级偏差却不一致,说明震级偏差大小不仅与量规函数、断裂带有关,还与反射波有关。
合肥肥东5次地震的震中距均达到反射波临界点,有部分反射波较强,部分反射波不强,该区震级偏小0.3—0.6,可能与量规函数偏小及地震波穿过郯庐断裂带有关(戴维乐,1986)。滕吉文等(1985)对马鞍山—常熟做人工爆破测线的地震记录表明:Δ=80—120 km,莫霍界面反射波较弱;Δ>120 km,莫霍界面反射波略有增强,是因为观测剖面经无锡—宿迁大断裂,而该断裂深达莫霍界面附近,介质变成破碎的不规则体,当地震射线穿过时,能量被强烈吸收。因此,肥东地震震级偏小应与地震射线穿过郯庐断裂有较大关系。同理,常州金坛、武进2个地震的震中距也达到反射波临界点,震级均偏小0.4,应与地震波横穿茅山东侧断裂带有关。
(3)震级偏差受震源机制的影响。合肥长丰和淮南谢家集区3个地震(震中距在181—204 km)的震级偏大0.3—0.4,方位角在305.5°—307.95°之间。查看波形发现,3个地震的S波较强,P波较弱。按照陈培善等(1983)的理论,3个地震的震源机制一致。前文所述2016年1月27日12:39南京建邺地震(图 3)比其他几个地震震级偏大的原因亦在于此。
(4)震级偏差受地质结构的影响。六安舒城县、金安区地震震中距约200 km,震级却偏小0.3—0.4,六安霍山县3个地震震中距在230—246 km,震级均偏小0.1—0.2(表 1)。如前文所述,该震中距范围的震级普遍偏大,相邻的金寨地震(震中距269 km)震级偏大0.3,还有1个金寨地震震级偏大0.1。六安地区周边断裂带较多,存在“霍山地震窗”,地震活动活跃,地质构造结构比较破碎,从而导致震级偏小,说明舒城、金安和霍山地区的地质结构比金寨地区破碎。但是邻近地区地震的震级偏差差异明显,可能与地质结构有较大差异有关,也可能与震源机制不一致有关,或者2种原因共同存在。因此,震级偏差的不同,可在一定程度上反映地质结构的差异。
4 结论综上所述,可以得出以下结论。
(1)通过分析震中距对震级偏差的影响,得出以下结果:①Δ<70 km,震级偏小,且震中距越小,震级偏差越大;②70≤Δ≤180 km,震级大部分偏小,但在反射波临界范围内,部分地震震级偏差较小,多在±0.2范围内摆动,可忽略;③Δ>180 km,震级普遍偏大。
(2)通过分析方位角对震级偏差的影响,得出以下结果:方位角≤66°时,震级偏差大于0的地震较多,方位角≥66°时,震级偏差小于0的地震较多,究其原因,与地震射线是否穿过郯庐断裂带和长江断裂有直接关系。
(3)综合分析震中距和方位角对震级偏差的影响,认为:量规函数、断裂带、反射波和震源机制均会对震级偏差产生影响;震级偏差不同可在一定程度上反映地质结构的差异。
论文对当涂站震级按震中距和方位角进行阐述,分析特点,寻找规律,总结相关经验,以便于今后分析同类地震时能起到参考作用。本研究建立在现有120个地震样本之上,观测资料有限,震中距分布不均匀、不密集,分析也不全面,结果可能存在偏颇,尚需今后收集足够多的震例,利用震级残差统计法对震级进行校正,或按照方位角进行校正。
曹复旺, 陈淑贞. 太原台近震震级偏差分析[J]. 地震地磁观测与研究, 1988, 9(1): 31-35. |
陈培善, 秦嘉政. 量规函数、台站方位、台基及不同测量方法对近震震级ML的影响[J]. 地震学报, 1983, 5(1): 87-98. |
陈运泰, 刘瑞丰. 地震的震级[J]. 地震地磁观测与研究, 2004, 25(6): 1-12. DOI:10.3969/j.issn.1003-3246.2004.06.001 |
戴维乐. 安徽台网近震震级ML的偏差分析[J]. 地震地磁观测与研究, 1986, 7(2): 1-9. |
傅承义, 陈运泰, 祁贵仲. 地球物理学基础[M]. 北京: 科学出版社, 1985: 1-447.
|
傅淑芳, 刘宝诚, 李文艺. 地震学教程[M]. 北京: 地震出版社, 1980: 198-216+157.
|
郭延杰, 包莹, 齐彬彬, 等. 赤峰中心地震台面波震级偏差分析[J]. 地震地磁观测与研究, 2020, 41(2): 57-61. DOI:10.3969/j.issn.1003-3246.2020.02.008 |
康清清, 顾勤平, 于悦颖, 等. 江苏及邻区地方性震级量规函数的研究[J]. 中国地震, 2019, 35(3): 521-530. DOI:10.3969/j.issn.1001-4683.2019.03.010 |
梁向军, 刘林飞, 张玲, 等. 山西地区近震震级偏差研究[J]. 山西地震, 2019(4): 5-7+12. DOI:10.3969/j.issn.1000-6265.2019.04.002 |
林仙坎. 闽台地区近震震级ML量规函数研究[J]. 中国地震, 2006, 22(3): 287-293. DOI:10.3969/j.issn.1001-4683.2006.03.009 |
刘瑞丰, 陈运泰, 任枭, 徐志国, 王晓欣, 邹立晔, 张立文. 震级的测定[M]. 北京: 地震出版社, 2015: 1-154.
|
刘阳, 周玲, 周雯, 等. 琼中地震台计算震级与中国地震台网中心测算震级差异的探讨[J]. 地震地磁观测与研究, 2010, 31(1): 25-28. DOI:10.3969/j.issn.1003-3246.2010.01.005 |
滕吉文, 孙克忠, 熊绍柏, 等. 中国东部马鞍山-常熟-启东地带地壳与上地幔结构和速度分布的爆炸地震研究[J]. 地球物理学报, 1985, 28(2): 155-169. DOI:10.3321/j.issn:0001-5733.1985.02.005 |
薛志照. 近震震级ML量规函数和台站校正值[J]. 华北地震科学, 1992, 10(1): 60-65. |
严尊国, 李普丽, 薛军蓉. 中国近震震级量规函数研究[J]. 中国地震, 1992, 8(4): 76-91. |
严尊国, 师蓉梅. 地方性均匀震级系统量规函数的区域特征[J]. 地震地磁观测与研究, 1983, 4(4): 4-10. |
严尊国. 湖北区域地震台网ML震级量规函数的修正[J]. 地震学刊, 1986(2): 9-16. |
张志斌, 朱皓清, 李艳永. 新疆数字地震台网地方性震级量规函数的初步研究[J]. 中国地震, 2018, 34(4): 667-675. |
Boore D M. Simulation of ground motion using the stochastic method[J]. Pure Appl Geophys, 2003, 160(1): 635-676. |
Helmberger D, Dreger D, Stead R, et al. Impact of broadband seismology on the understanding of strong motions[J]. Bull Seismol Soc Am, 1993, 83(3): 830-850. |
 2021, Vol. 42
2021, Vol. 42

