强震前的地震矩加速释放(accelerating moment release,AMR)现象被认为是一种有潜力的中期地震前兆异常(Sornette et al,1995),在物理上可与地震孕育过程中的“临界性”联系在一起。AMR现象及其相关讨论已引起广泛关注,这很大程度上在于其在地震预测研究中所展示的应用潜力。国内外许多研究者已基于AMR现象提出了相关分析方法,并已应用于不同地区的诸多震例(Bufe et al,1993, 1994;Sornette,1995;Brehm et al,1998;杨文政等, 1999, 2000;蒋长胜等, 2004, 2009, 2011;王亚茹等,2014;李霞等,2015;常明等,2016;王亮等,2017)。上述研究表明,AMR现象在中强震前具有一定普遍性,它在对未来发震地点预测方面具有一定潜力。
2010年河津4.8级地震前1年在震区附近出现地震矩加速释放现象,表明AMR现象在山西地区中等地震前可能有一定的预测效果,但迄今为止未见对山西地区中等地震进行的震例研究。因此,本文对1970年以来山西地区及邻区ML≥5.0地震进行AMR现象的回溯性研究,通过尝试选取不同研究半径和时间窗长,考察累积benioff应变释放(CBS)曲线的加速程度,最终遴选出这些地震前出现明显加速矩释放现象的优势研究半径,并讨论AMR现象在山西地区的普遍性。
1 地震矩加速释放(AMR)现象和释放程度Varnes(1989)、Bufe等(1993)和Bufe等(1994)将AMR现象的分析表示成“破裂时间分析”方程,即
| $ \sum \mathit{\Omega} = A + B{\left( {{t_{\rm{f}}} - t} \right)^m} $ | (1) |
式中,Ω为地震活动性的量度,如地震矩(或地震能量)、地震数目或Benioff应变等;A、B为常数;幂指数m为地震矩释放程度;tf为大地震发生的时间。m表示地震矩释放曲线的类型,当m<1时,累积Benioff应变释放(CBS)曲线呈现“加速”行为;m>1时为“减速”;而当m≈1时CBS释放曲线呈线性。利用式(1)可研究强震的发生时间、震级及未来强震的发生地点(蒋长胜等,2009)。m值也被称为“地震矩释放程度”。在利用AMR现象对主震发震时间和震级进行预测时,震前加速地震序列的时间和空间尺度的选取准则为,通过多个时间和空间尺度来观察震前地震序列的矩释放规律,使地震矩释放曲线的拟合达到“最佳解”时的时间和空间参数。
目前的研究中主要以Benioff应变作为地震活动性的量度,用来计算地震矩释放程度m。因此,下文先给出Benioff应变的计算公式。
采用如下经验关系计算地震矩
| $ \lg {M_0} = 1.5{M_{\rm{L}}} + 9.05 $ | (2) |
其中,M0的单位为N•m。
根据经验关系由地震矩计算出地震波能量
| $ E = 5.0 \times {10^{ - 5}}{M_0} $ | (3) |
Benioff应变定义为地震波能量的平方根,拟合式(1)可计算出常数A、B、地震矩释放程度m以及大地震的发生时刻tf。
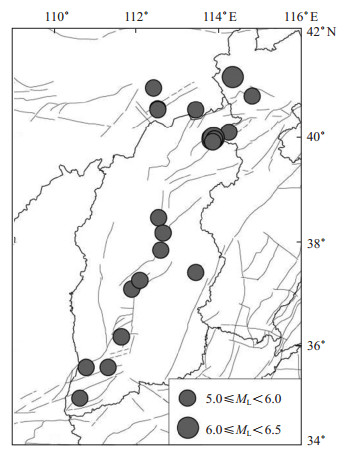
2 震例和资料选取选取山西及邻区1970年以来ML≥5.0地震作为研究对象,去除主震的较大余震后,共22次地震(图 1)。本文对上述地震进行AMR回溯性研究。
|
图 1 山西及邻区ML≥5.0地震震中分布 Fig.1 The ML≥5.0 earthquakes distribution of Shanxi and adjacent area |
采用中国地震台网中心提供的1970年1月至2018年12月的全国地震目录,采用K—K法对山西及邻区ML≥5.0地震进行余震删除处理。另外,笔者(王霞等,2014)曾对山西及邻区1970年以来地震目录的最小完整性震级进行过研究,认为该地区的最小完整性震级为ML 2.5,因此,把ML 2.5作为计算Benioff应变释放的最小完整性震级。
3 不同时空尺度的矩释放特征分别以不同时间尺度、以震中为圆心的不同研究区半径对山西及邻区AMR现象进行考察。由于研究震例的最大震级为6.2级,根据Bowma等(1998)的震级M与搜索半径R之间的经验关系式,可将多尺度的扫描半径设定为80 km、100 km、120 km、150 km,分别计算震前6 a、4 a、2 a、1 a的Benioff应变释放情况,分析地震矩释放程度m的变化特征。通过计算后认为扫描半径为120 km时,地震矩释放现象较明显,因此,下文只列出研究半径为120 km的m值计算结果(表 1)。
| 表 1 山西及邻区ML≥5.0地震的m值 Table 1 The statistics of m-value for ML≥5.0 earthquakes in the Shanxi and adjacent area |
在上述22个震例中,有12个在主震前Benioff应变释放曲线呈现加速释放或由减速释放过渡到加速释放的特征,约占55%;有7个呈现减速释放或由加速释放过渡到减速释放或由减速释放过渡到匀速释放的特征,约占32%;有1个震例呈现由加速释放过渡到匀速释放的特征,约占4%;有2个震例由于数据太少而无法计算m值,从而无法判断Benioff应变释放特征,约占9%。另外,随着时间不断接近主震,约有一半震例显示地震矩加速释放程度m值发生变化,即Benioff应变释放出现不同的特征,且Benioff应变无论从加速释放过渡到减速释放,还是从减速释放过渡到加速释放,多数发生在主震前1—2 a内。
从震例的空间分布来分析AMR的释放特征,可将研究区域分为山西北区、中区和南区。结果显示,在山西北区的13个震例中,有5个震例前Benioff应变释放出现加速释放或由减速释放过渡到加速释放(其中,3个属于内蒙古,1个属于河北,1个属于山西);山西中区5个震例中,有4个震例前出现加速释放或由减速释放过渡到加速释放过程;山西南区4个震例中,有3个震例在震前出现加速释放或由减速释放过渡到加速释放。从现有的震例来看,山西中、南区震例出现AMR加速释放特征的比例相对高;而在山西北区震例中位于山西境内的共有5个(包括4次大同—阳高地震和1991年忻州地震),仅在忻州地震前1年出现Benioff应变加速释放,而4次大同—阳高地震前均呈现Benioff应变减速释放。
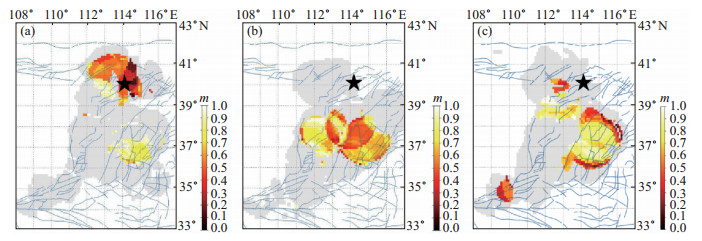
本文还将讨论地震矩释放空间异常区与未来主震之间的关系。通过上文分析可知,AMR现象多在主震前1—2 a发生变化,考虑到AMR为中期地震前兆异常,因此将讨论震前1年、半年、3个月和临震前m值空间变化特征。对22个震例的回溯研究结果表明,有以下4种情况:①震前1年到临震前出现不同时段的低m值区域,且主震震中位于大范围椭圆形异常区内或边缘,共有14个震例(图 2);②震前半年到临震前出现的大范围类椭圆形的低m值区域,共有3个震例(图 3);③震前3个月到临震前出现的类椭圆形的低m值区域,共有2个震例(图 4);④有3个震例在震前1年到临震前均没有出现低m值区域,分别是1971年内蒙古卓资4.7级地震、1998年河北张北6.2级地震和2010年山西大同阳高4.6级地震。
|
图 2 1989年大同—阳高6.1级地震震前地震矩释放空间扫描 (a)震前1年;(b)震前半年;(c)震前3个月 Fig.2 Seismic moment release maps before the 1989 Datong-Yanggao M 6.1 earthquake |
|
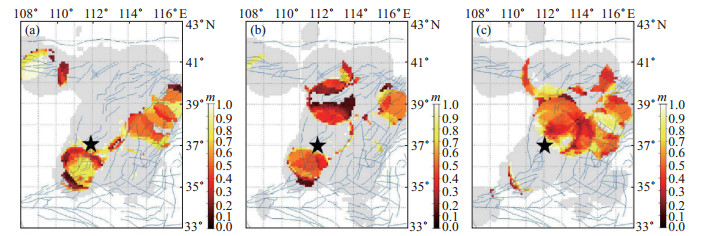
图 3 1980年平遥4.6级地震震前地震矩释放空间扫描 (a)震前半年;(b)震前3个月;(c)临震前 Fig.3 Seismic moment release maps before the 1980 Pingyao M 4.6 earthquake |
|
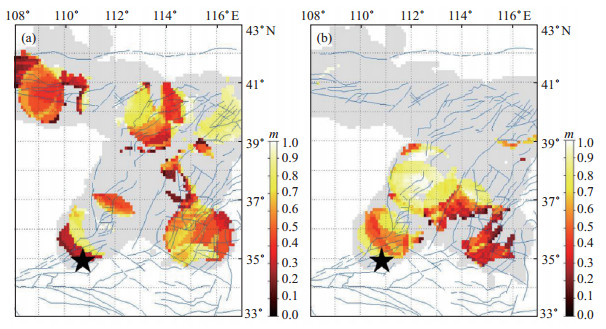
图 4 1998年永济4.6级地震震前地震矩释放空间扫描 (a)震前3个月;(b)临震前 Fig.4 Seismic moment release maps before the 1998 Yongji M 4.6 earthquake |
通过对山西及邻区22次ML≥5.0地震震前不同时间段的累积Benioff应变释放情况进行分析,认为山西及邻区约55%震例前存在地震矩释放加速现象(AMR),且Benioff应变释放特征的变化多出现在地震前1—2 a内。同时,从空间上也分析了地震矩释放与主震间的关系,发现大部分地震震前1年内在震中附近区域出现大范围椭圆形的低m值区域,且主震震中位于该异常区的内部或边缘。综上认为,地震矩加速释放现象在山西及邻区具有一定的普遍性,且为中期地震前兆异常,研究结果可为震情跟踪的地点判定提供参考依据。
常明, 李芳芳, 张锦玲, 等. 2000年9月12日青海兴海6.6级地震的"回溯性"地震矩加速释放研究[J]. 防灾减灾学报, 2016, 32(2): 15-21. |
蒋长胜, 吴忠良, 史勇军. 中强震前地震活动矩释放加速现象(AMR)的普遍性问题[J]. 中国地震, 2004, 20(2): 119-125. DOI:10.3969/j.issn.1001-4683.2004.02.001 |
蒋长胜, 吴忠良. 强震前的"加速矩释放"(AMR)现象: 对一个有争议的地震前兆的回溯性震例研究[J]. 地球物理学报, 2009, 52(3): 691-702. |
蒋长胜, 吴忠良. 2010年玉树MS 7.1地震前的中长期加速矩释放(AMR)问题[J]. 地球物理学报, 2011, 54(6): 1501-1510. DOI:10.3969/j.issn.0001-5733.2011.06.009 |
李霞, 蒋长胜, 闫德桥, 等. 1989年以来华北地区中强震前地震矩加速释放空间扫描特征的研究[J]. 地震研究, 2015, 38(3): 359-369. DOI:10.3969/j.issn.1000-0666.2015.03.004 |
王亮, 王岩, 钱蕊, 等. 辽宁地区5级地震前加速矩释放现象的"回溯性"研究[J]. 防灾减灾学报, 2017, 33(1): 12-16. |
王霞, 宋美琴, 李丽, 等. 山西地区不同时段地震目录最小完整性震级研究[J]. 地震, 2014, 34(2): 82-88. |
王亚茹, 张素欣, 刘晓丹, 等. 华北地区地震活动矩加速释放现象的震例研究[J]. 高原地震, 2014, 26(3): 27-32. |
杨文政, 马丽. 地震活动加速模型及其在中国的应用[J]. 地震学报, 1999, 21(1): 32-41. |
杨文政, Vere-Jones D, 马丽, 等. 一个关于临界地震的临界区域判别的方法[J]. 地震, 2000, 20(4): 28-38. |
Bowman D D, Ouillon G, Sammis C G, et al. An observational test of the critical earthquake concept[J]. J Geophys Res, 1998, 103(B10): 24359-24372. |
Brehm D J, Braile L W. Intermediate-term earthquake prediction using precursory events in the New Madrid seismic zone[J]. Bull Seismol Soc Am, 1998, 88(2): 564-580. |
Bufe C G, Varnes D J. Predictive modeling of the seismic cycle of the greater San Francisco Bay Region[J]. J Geophys Res, 1993, 98(B6): 9871-9883. |
Bufe C G, Nishenko S P, Varnes D J. Seismicity trends and potential for large earthquakes in the Alaska-Aleutian region[J]. Pure Appl Geophys, 1994, 142(1): 83-99. DOI:10.1007/BF00875969 |
Sornette D, Sammis C G. Complex critical exponents from renormalization group theory of earthquakes: implications for earthquake predictions[J]. J de Physique I, 1995, 5(5): 607-619. |
Varnes D J. Predicting earthquakes by analyzing accelerating precursory seismic activity[J]. Pure Appl Geophys, 1989, 130(4): 661-686. |
 2021, Vol. 42
2021, Vol. 42


