2. 中国上海 200062 上海佘山地球物理国家野外观测研究站
2. Shanghai Sheshan National Geophysical Observatory, Shanghai 200062, China
地震台阵是为监测微弱地震信号发展起来的地震观测系统。上海佘山地震台阵于2001年10月通过验收并正式投入运行,是我国第一个永久性三分量宽频带台阵。该台阵位于上海佘山地区,由16个子台组成,孔径约3 km。自台阵投入运行以来,存储了大量地震事件信息及噪音数据。
近年来,为了充分利用数据资料并更新台阵仪器设备,上海市地震局开展一系列措施,对佘山地震台阵进行改造,并完成新版数据处理系统软件。数据处理系统开发人员将压缩感知算法加入其中,用以得到高分辨率的地震反方位角。压缩感知算法并不是一个新兴的数据处理算法,该算法基于信号的稀疏性,配以合适的采样方法获取离散信号,并完整重建信号(Donoho,2006),在地震学研究领域得到广泛应用,如:Yao等(2011)将压缩感知方法用于日本9.0级大地震数据,提出与频率相关的破裂模型;孔丽云等(2012)将压缩感知算法用于地震信号重建;贺月等(2020)将压缩感知算法用于地震资料去噪。
本研究着重将压缩感知算法用于上海佘山地震台阵收集的远震地震数据,获得高分辨率最优反方位角和慢度,重新定位震源位置,并与传统计算方法,如:频率—波数分析、时间域波形聚束分析法得到的结果进行比较,判定该方法在远震数据处理中的有效性。
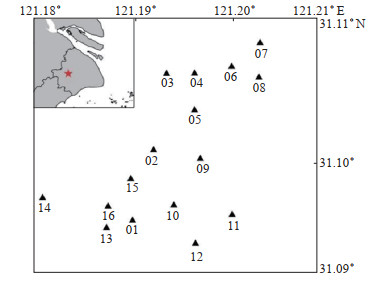
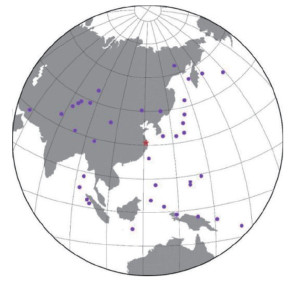
1 数据与方法 1.1 数据选取上海佘山地震台阵由16个台间距约600 m的子台组成,孔径约3 km,仪器频带范围为120 s—50 Hz,子台分布见图 1。选取2001—2005年该台阵记录的MS 5.5以上远震,根据震级大小、地震波走时、事件分布,筛选得到45个远震事件,采用压缩感知算法,计算反方位角和慢度值,并与频率—波数分析、时间域波形聚束分析法计算得到的结果进行比较。远震分布见图 2,图中五角星为上海佘山地震台阵位置,紫色圆点为最终筛选出来的远震事件。将整理的地震事件波形数据转换为SAC格式,进行去除仪器响应、去均值、去倾斜和带通滤波等预处理,并将所有子台的采样间隔统一为0.01 s。
|
图 1 上海佘山地震台阵位置分布 Fig.1 Location of Shanghai Sheshan Seismic Array (SSSA) |
|
图 2 所选取远震分布 Fig.2 Epicentres of earthquakes used in this study |
压缩感知算法又被称为压缩采样算法,利用信号的稀疏特性,在远小于Nyquist采样率的条件下,用随机采样获取信号的离散样本,降低数据量,通过非线性重建算法重建信号,使得时域波形精确恢复且频率信息不丢失(宋寿鹏等,2016)。就空间谱估计观点而言,震源(或破裂过程)能量辐射位置的稀疏性是一个欠定的线性逆问题,通过对角度个数的稀疏限制,可以完成压缩感知的波达方向估计。
将震源(能量辐射)的可能位置划分为M个网格点,每个网格点具有特定的慢度和反方位角,其复震源向量为xi(ω),其中i =1,2,...,M,ω为圆频率(姚华建,2013)。若N个台站接收的振幅谱向量d(ω)为所有可能网格点的源谱经相移后叠加的能量,频率域上的相移即为时间上的时移,则d(ω)可以表示为
| $ \mathrm{d}(\omega)=G(\omega) x(\omega)+E(\omega) $ | (1) |
式中,G(ω)为传播矩阵,其第nm个元素为
考虑到震源网格点的数目M大于观测台站的数目N,且地震破裂过程中能量辐射(震源)位置具有稀疏性,因此,基于L1范数的反演问题可以写为
| $ \tilde{x}(\omega)=\arg \min \|x(\omega)\|_{1} \quad \text { s.t. } \quad\|G(\omega) x(\omega)-\mathrm{d}(\omega)\| <\varepsilon $ | (2) |
Tropp等(2007)采用OMP算法计算上述反演问题。对每一个频率做一次反演,最后将所有的解,即能量最大的点以及超过最大能量95%以上的点拾取出来,得到最终的源信号图谱。
2 压缩感知结果分析选择的45个地震事件震中位置由美国地质调查局(USGS)提供,利用佘山台阵01子台经纬度,计算得到事件的反方位角,作为该事件的实际反方位角。利用压缩感知方法(CS方法)、频率—波数分析(F—K分析)、时间域波形聚束分析(Beamforming分析)方法分别计算反方位角,并与实际反方位角进行对比分析。表 1详细列举了USGS提供的45个地震的定位结果以及计算得到的实际反方位角和利用CS方法、F—K分析和Beamforming分析计算所得最优反方位角和慢度值。选取接近实际值的最优反方位角,作为参与地震定位的反方位角,结合P波、S波到时差与震中距的关系进行地震定位(S-P定位)。由于该定位方法相当于单台定位,只能固定震源深度(33 km),得到理论的P波、S波到时差,因此,深源地震的定位结果精度较差,文中仅给出定位地震的震中位置。在表 1中标出了最终S-P定位时用于计算反方位角的算法。
| 表 1 选取的45个地震定位结果比较 Table 1 Comparison of location results of 45 selected earthquakes with different methods |
由表 1可知,在45个地震事件中,参与定位的最优反方位角中有23个是通过CS方法计算的,7个是通过F—K分析计算的,15个是通过Beamforming分析测定的。在13个MS 7.0以上远震事件中,Beamforming和CS方法所测反方位角较为一致,且数值大小接近实际反方位角;在部分MS 7.0以上地震中,F—K分析计算的反方位角与实际数值有所偏差;而对于MS 7.0以下地震,CS方法、Beamforming、F—K分析法在个别地震中适用性均较差。P波初动清楚、信噪比高的地震事件,采用以上3种方法计算的反方位角一致性较好;信噪比相对较低、P波初动复杂的地震事件,采用3种方法计算的反方位角偏差较大。
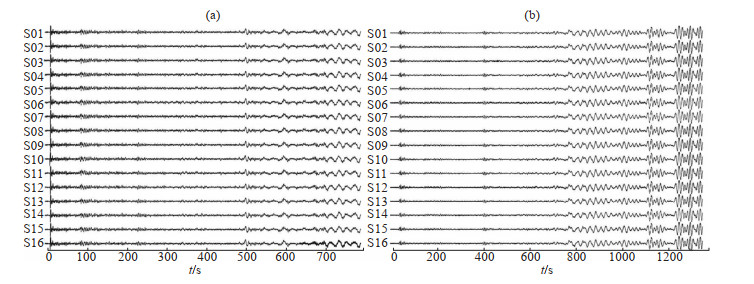
以上海佘山地震台阵记录的2002年10月11日印度尼西亚伊里安地区MS 6.0地震和2003年科曼多尔群岛MS 6.7地震为例,对压缩感知结果进行分析。2次地震原始波形及压缩感知分析结果见图 3、图 4。
|
图 3 上海佘山地震台阵记录的2次远震震例波形 (a)2002年10月11日印度尼西亚伊里安地区MS 6.0地震波形;(b)2003年12月6日科曼多尔群岛MS 6.7地震波形 Fig.3 examples of teleseismic waveform data recorded by SSSA |
|
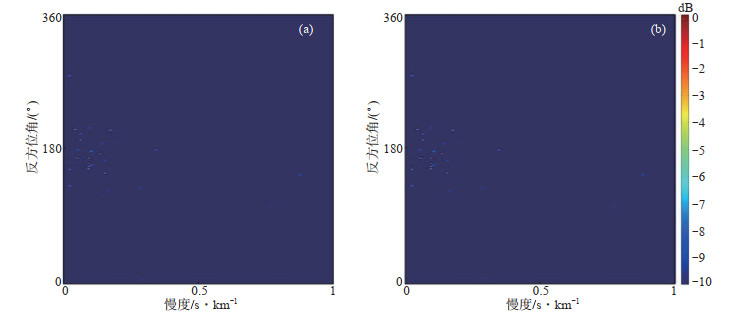
图 4 2次震例的压缩感知分析结果 (a)2002年10月11日印度尼西亚伊里安地区MS 6.0地震波形;(b)2003年12月6日科曼多尔群岛MS 6.7地震波形 Fig.4 Compressed sensing analysis results of the 2 earthquakes |
(1) 震例1:2002年10月11日印度尼西亚伊里安地区MS 6.0地震。由图 3(a)可见,该地震事件波形初至清晰,信噪比较好。在进行压缩感知算法处理时,选择的时间窗长度约12 s,是因为该窗口可截取完整的初至P波震相。在进行压缩感知计算时,慢度搜索范围为(0,1),搜索点数为100个,反方位角搜索范围为(0°,360°),迭代次数为1 000次,计算频率范围为(0.1 Hz,10 Hz),收敛精度为10-6。对每个频率做一次反演,将所有解,即能量叠加在一起,拾取能量最大的点以及超过最大能量95%以上的点,得到最终信号源的位置,也就是带有慢度和反方位角的信号源,即震源信息,见图 4(a)。由图 4(a)可见,能量主要集中在反方位角150°—210°和慢度0—0.2 s/km范围内,在此范围内有大量色块显示,表明该地震初至P波在频率上具有复杂性,并非单一频率的初至波形。在该范围内找到能量最大的点(图中颜色最红的点)即为该地震基于压缩感知算法的最优解,其最优反方位角为156.44°,最优慢度值为0.071 s/km,与实际反方位角156.95°基本一致。而由传统的F—K方法计算的反方位角为183.15°,聚束方法计算的反方位角为168.47°,与实际反方位角相比,误差均比压缩感知方法大。根据CS算法计算结果,利用S-P定位算法得到地震位置为(1.36°S,134.32°E),与USGS给出的结果(1.48°S,134.11°E),误差在1°范围内。
(2) 震例2:2003年12月6日科曼多尔群岛MS 6.7地震。由图 3(b)可见,上海佘山地震台站记录的此次地震事件波形P波初动清晰,与伊里安地震相比,信噪比稍低。此次地震P波初至震相振幅比后至震相振幅小,可能会对需要能量信息的压缩感知方法带来负面影响。同理,得到此次地震的能量分布结果,见图 4(b)。由图 4(b)可见,能量主要集中在反方位角0—90°和慢度0—0.1 s/km范围上。在该范围内找到能量最大的点,即为该地震基于压缩感知算法的最优解,最优反方位角为31.09°,最优慢度值为0.071 s/km,与实际反方位角38.58°有一定偏差。而利用F—K方法和聚束方法得到的反方位角分别为56.40°和29.08°,均与实际反方位角偏差较大。根据CS算法计算结果,利用S-P定位算法得到地震位置为(59.92°N,161.88°E),与USGS给出的定位结果(55.54°N,165.78°E)较为接近,误差约4°,可能由上述P波初至震相振幅相对较小所致。
3 讨论与结论本研究选取2001—2005年全球MS 5.5以上地震,根据震级大小及地震分布,筛选得到45个地震事件,结合USGS给定的地震震中位置,利用佘山台阵子台S01的位置信息,计算各地震实际反方位角值,分别采用频率—波数分析(F—K分析)、时间域波形聚束分析法(beamforming)、压缩感知(CS方法)等方法,计算反方位角和慢度,并与实际反方位角数值进行对比分析。
F—K分析和聚束分析是地震台阵数据处理的2种基本方法。选择地震P波震相进行F—K分析时,时间窗应尽量包含该震相的全部波形,且窗长不能过长(于海英等,2005)。对于远震波形而言,利用F—K分析,大尺度台阵分析处理效果较好,作为小尺度台阵的佘山台阵分析效果一般。而聚束方法放大了具有适当慢度的震相,同时压低了不相干噪声和有不同慢度的震相,具有在相加波形中得到清楚的大振幅波形的优点。使用聚束处理,地震台阵的作用表现为波数滤波器,噪声被压低的程度取决于参与处理的台站个数M。聚束分析处理后,台站信噪比S与单个地震台站信噪比s的关系是
压缩感知方法作为一种稀疏采样方法,存在稀疏采样的共性问题。对于多震源点事件,该方法较F—K分析具有一定优势,在选择的时窗内能量最大的点以及超过最大能量95%以上的点也可以拾取出来,如图 4所示,该段时窗内可以存在不同震相(Hu et al,2019)。但一般只选取能量最大的点作为最优反方位角的解。
通过分析不同方法计算最优反方位角,进行对比分析可得到以下结论。
(1) 压缩感知方法在地震台阵的远震定位中表现良好。45个最优结果中有23个地震事件采用压缩感知方法计算的反方位角来进行定位;15个地震事件采用聚束方法计算的反方位角来进行地震定位;7个地震事件采用F—K方法计算的反方位角来进行地震定位。在45个地震中,利用CS方法获得的反方位角接近实际反方位角的个数更多。
(2) 对于信噪比高的地震事件,压缩感知、聚束、F—K方法得到的反方位角一致性较好;信噪比相对较低、P波初动复杂的地震事件,利用3种方法计算的反方位角偏差均较大,而压缩感知方法的分辨率相对较高。
(3) 利用台阵处理软件中的压缩感知方法,能够清晰显示所选取时窗内地震能量的集中区域。根据其能量分布判断,时窗内P波波段在频率上具有复杂性,并非单一频率的初至波形。
(4) P波初至震相振幅相对较小时,可能导致拾取的能量最大点并非实际P波初至震相产生的能量点,而利用该反方位角进行地震定位,所求震中会与实际位置有所偏差。
贺月, 周健, 陈力鑫, 等. 基于压缩感知的OMP算法在地震资料中的去噪效果分析[J]. 油气地球物理, 2020, 18(2): 92-95. |
孔丽云, 于四伟, 程琳, 杨慧珠. 压缩感知技术在地震数据重建中的应用[J]. 地震学报, 2012, 34(5): 659-666. DOI:10.3969/j.issn.0253-3782.2012.05.007 |
宋寿鹏, 邵勇华, 堵莹. 采样方法研究综述[J]. 数据采集与处理, 2016, 31(3): 452-463. |
姚华建. 用压缩感知方法研究大地震的破裂过程——方法与研究进展[J]. 中国科学技术大学学报, 2013, 43(11): 907-921. DOI:10.3969/j.issn.0253-2778.2013.11.006 |
于海英.数字化地震资料应用研究[D].上海: 同济大学, 2005.
|
Donoho D L. Compressed sensing[J]. IEEE Trans Inform Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
Hu Jing, Zhang Haijiang, Yu Haiying. Accurate determination of P-wave backazimuth and slowness parameters by sparsity-constrained seismic array analysis[J]. Geophysical Journal International, 2019, 216(1): 1-18. |
Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Trans Inf Theory, 2007, 53(12): 4655-4666. DOI:10.1109/TIT.2007.909108 |
Yao H J, Gerstoft P, Shearer P M, et al. Compressive sensing of the Tohoku-Oki MW 9.0 earthquake:Frequency-dependent rupture modes[J]. Geophys Res Lett, 2011, 38(20): L20310. DOI:10.1029/2011GL049223 |
 2020, Vol. 41
2020, Vol. 41


