2. 中国黑龙江 154101 鹤岗地震台;
3. 中国北京 100081 中国地震局地球物理研究所
2. Hegang Seismic Station, Heilongjiang Province 154101, China;
3. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China
地震台阵可以降低全球地震(核爆)的检测下限,改进地球地壳速度结构模型,提高区域尺度层析成像分辨率(郝春月,2016)。把台阵作为加强台站并入地震台网,可提高台网测定能力(郝春月等,2006;郑重等,2014)。为了实施国家地震科技创新工程——“透明地壳”计划,提升我国对全球微小地震的监测能力,中国地震局拟在黑龙江鹤岗等地建设地震台阵。
2019年4月8日—5月13日,黑龙江省地震局经过对新华农场、萝北山河村、三道林场等7个场地的实地踏勘,初步将台阵场址定在鹤岗市西部三道林场。该场址与市中心直线距离约20 km,场地附近无干扰源,观测环境良好。场地覆盖层厚约0.5 m,其下为风化的花岗岩,有的测点基岩出露,比较适宜观测。地质考察结果显示,场地附近无断裂穿过。
场地勘址首先应建立信号及噪声的相关性曲线,这是确定台阵布局的关键依据(郝春月等,2002b)。本文对鹤岗地震台阵勘选过程中记录的近震和远震波形信号及噪声进行处理、分析,得到信号及噪声在两两子台的相关系数,进而计算台阵对近震和远震的最佳监测距离,从而为地震台阵布局设计提供依据。
1 勘址布局与观测在三道林场,将鹤岗地震台阵设计为NORESS同心圆型,包括1个中心点、4个环,共25个子台。从内到外,各环子台数分别为1、3、5、7、9,环上各子台站点均匀分布,以保证能测定来自各个方向的地震事件的方位角和慢度。本次三道林场勘选共布设9个子台,分别是sdzx、sd1-2、sd2-5、sd3-2、sd3-4、sd3-6、sd4-3、sd4-6、sd4-9[图 1(a)],初选原则是保证各环均有子台的基础上,从内环到外环子台个数依次增加,使得台阵内点间距离覆盖从最小到最大范围。观测时间为2019年5月11日—24日,使用仪器为CMG-3T宽频带地震计及REFTEK-130s数据采集器。

|
图 1 勘选站点和记录的典型地震分布 Fig.1 Distribution of the survey sites and recorded typical earthquakes |
地震台阵选址首先应考虑各子台观测场地的背景噪声是否符合建设标准。评估背景噪声有2个指标:①环境地噪声水平Enl值,若Enl < 3.16×10-8 m/s,则地噪声水平为Ⅰ级;②5 Hz处垂直向加速度地噪声功率谱值,该值需小于-135 dB。
随机选择5月23日(国际时00:00—23:59即北京时23日8:00—24日7:59)的24个数据样品时段,按背景噪声评估指标,计算9个子台的Enl值及地噪声功率谱,评估结果见表 1。
| 表 1 各子台背景噪声指标 Table 1 Background noise index of each sub-station |
由表 1可见,除sd3-6外,其他各子台测点的环境地噪声水平在绝大多数时段均达到Ⅰ级;垂直向地噪声功率谱在5 Hz处均小于-135 dB。考虑到sd3-6勘选站点在道路边,过往车辆干扰较大,计划后期更改该点位。经对各子台背景噪声的分析,认为该场地符合国际监测系统(IMS)规定的建设标准(郑重等,2000;郝春月等,2002a;郑重等,2016)。
提取在台阵勘选期间记录清晰的4次典型地震波形进行分析,其中1次近震、3次远震。勘选站点及典型地震分布见图 1,地震参数见表 2。
| 表 2 勘选期间记录的典型地震 Table 2 Typical earthquakes recorded during the survey |
在时间域中求2个随机信号的相关函数,习惯把信号离散化,也就是数字化。假设采样周期ΔT已知,则将2个随机信号x(n)、y(n)的相关函数定义为
| ${R_{xy}}\left({p\Delta T} \right) = {R_{xy}}\left({{\tau _p}} \right) = \frac{1}{{{\sigma _x}{\sigma _y}N}}\sum\limits_{n - 1}^N {{x_n}{y_n}} $ | (1) |
也就是要计算两信号相同时刻(无延迟)的相关函数。由于x(n)、y(n)是数字化零均值样品,则更直观地计算公式(郝春月等, 2003, 2006)为
| ${R_{xy}}\left({{\tau _p}} \right) = \frac{{\sum\limits_{i = 1}^N {\left[ {x\left(i \right) - \bar x} \right]\left[ {y\left(i \right) - \bar y} \right]} }}{{{{\left\{ {\sum\limits_{i = 1}^N {\left[ {x\left(i \right) - \bar x} \right]} } \right\}}^{1/2}}{{\left\{ {\sum\limits_{i = 1}^N {\left[ {y\left(i \right) - \bar y} \right]} } \right\}}^{1/2}}}}$ | (2) |
在频率域,经常用可用功率谱表示相干函数rxy (f)。相干函数rxy (f)给出了2个随机信号在频率域的相似性,其中f代表信号频率。一般,相干函数在0—1之间变化。若两信号完全不相关,则相干函数值为零。对于2个相同信号,其相干函数为1。则相干函数定义为
| ${r_{xy}}\left(f \right) = \frac{{|{G_{xy}}\left(f \right)|}}{{\sqrt {{G_{xx}}\left(f \right){G_{yy}}\left(f \right)} }}$ | (3) |
式中,Gxx (f)和Gyy (f)分别为两随机信号x(t)和y(t)的自功率谱密度,Gxy(f)为其互功率谱密度。
2.3 台阵增益理论一般,地震台阵各子台的主要功能是监测初至P波信号,而子台监测能力受台阵增益控制,台阵增益可以通过计算聚束过程中的信噪比(SNR)得到。通过聚束的SNR增益G可如下表示
| ${G^2} = \frac{{\sum\nolimits_{ij} {{\omega _i}{\omega _j}{C_{ij}}} }}{{\sum\nolimits_{ij} {{\omega _i}{\omega _j}{\rho _{ij}}} }}$ | (4) |
式中,Cij和ρij分别表示一个地震台阵内传感器i和j之间的信号互相关值和噪声互相关值,ωi为传感器权重,一般ωi = 1。传感器记录的信号和噪声的自相关值均为1,则式(4)可以写为以下简单形式
| ${G^2} = \frac{{1 + \left({N - 1} \right)\bar C}}{{1 + \left({N - 1} \right)\bar \rho }}$ | (5) |
式中,C和ρ分别表示平均信号互相关值和平均噪声互相关值,N为传感器数目。
对于任意形状的台阵,若已知台阵布设的所有传感器两两组合间的信号互相关值和噪声互相关值,则可以根据公式(5)估计其台阵增益。
3 信号及噪声的相关性分析相关性分析是台阵布设的测点中任意2个测点间的相关关系,一般有2种:①信号及噪声在时间域中的相关性分析;②信号及噪声在频率域中的相关性分析。下文分别对这种相关性进行分析和讨论。
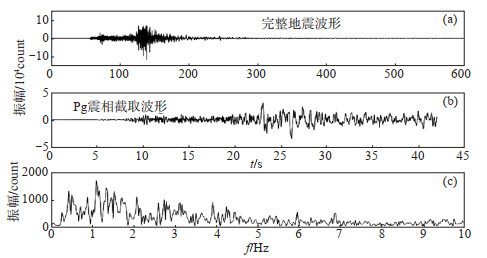
3.1 时间域相关性分析 3.1.1 近震Pg震相以2019年5月18日松原5.1级地震(近震)为例,震中距约500 km,分析sd1-2和sd2-5(两点间距为587 m)2个测点记录的Pg震相相关性。对sd1-2和sd2-5测点记录的原始波形数据进行预处理,包括去均值、去趋势项,截取Pg震相传播42 s的波形数据,采用四阶butterworth滤波器,对2个时间序列做带通滤波,计算二者的相关系数,分析两信号在特定频段的相关性。一般认为近震优势频段在1—10 Hz,因此对该频段波形进行带通滤波,计算得到sd1-2和sd2-5的相关系数为0.728 4。文中仅给出sd1-2测点波形记录的幅频分析结果,可见观测波形优势频段在0.2—4 Hz[图 2(c)]。取1—10 Hz和0.2—4 Hz频段的交集,即可得1—4 Hz为滤波频段,sd1-2和sd2-5测点的相关系数提升到0.846 7。因此,确定滤波频段为1—4 Hz。
|
图 2 sd1-2数据预处理及幅频曲线 (a)完整波形;(b)Pg震相截取波形;(c)截取波形频谱曲线 Fig.2 Preprocessed and amplitude-frequency curves of records at sd1-2 |
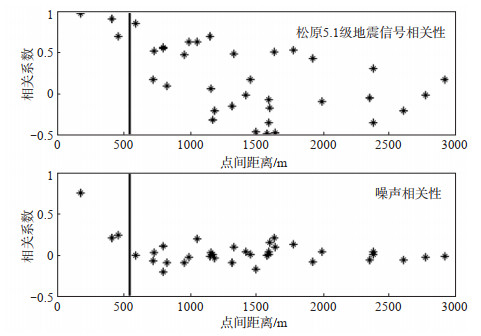
以测点间距为横坐标,信号及噪声的相关系数为纵坐标,得到松原5.1级地震的Pg震相波形信号及噪声在所有测点不同点间距的相关性散点图,结果见图 3。由图 3可见,测点间距大于550 m,近震Pg震相的相关系数显著下降,同时,噪声相关系数显著下降,而在测点间距为550 m时,两点的相关系数接近0,且信噪比最高。因此,在鹤岗三道林场台阵监测近震Pg震相,两测点的最佳距离应约为550 m。
|
图 3 松原5.1级地震的Pg震相信号及噪声在不同测点间距的相关性 Fig.3 The correlation of Pg phase signal and noise at different distances for SongYuan 5.1 earthquake |
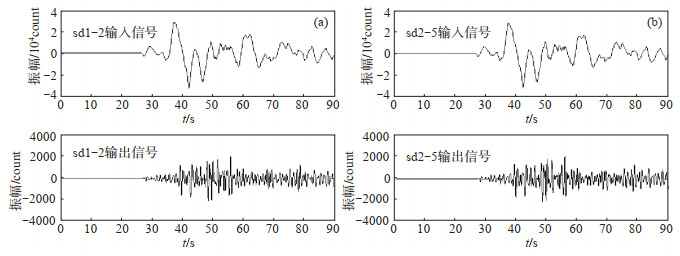
以2019年5月14日新不列颠7.1级地震为例,分析远震P波震相信号及噪声在两两子台的相关性。同理,对波形数据进行去均值、去趋势性等预处理,截取P波震相波形时段,进行Butterworth四阶带通滤波,一般认为0.8—2.5 Hz是远震的优势频段,因此选择该频段提取P波震相(图 4),计算sd1-2和sd2-5测点(点间距为587 m)的相关系数。结果显示,2测点记录的相关系数为0.846 7。
|
图 4 sd1-2、sd2-5测点的原始输入波形与滤波后输出波形 Fig.4 The original input waveforms and the filtered output waveforms at sd1-2 and sd2-5 |
以两测点的不同间距为横坐标,信号及噪声两两测点(子台)的相关系数为纵坐标,得到二者的相关系数散点图,见图 5。由图 5可见,点间距从1 570 m开始,P波震相的相关系数显著下降,同时噪声相关系数接近0。因此,确定监测远震的两子台最远距离不超过1 570 m。

|
图 5 新不列颠地震P波信号及噪声在不同点间距的相关系数 Fig.5 The correlation of P phase signal and noise at different distances for New Britain earthquake |
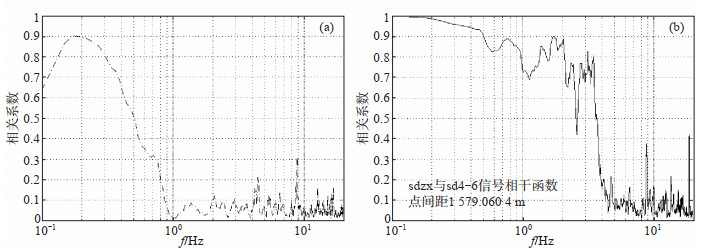
相干函数可以反映波形信号在不同频率的相关性。计算sdzx与sd4-6测点(子台)间2019年5月23日的(随机)背景噪声相干函数和2019月5月14日20:58新不列颠7.1级地震信号相干函数(图 6),采用移动平均法对相干函数值进行平滑,窗长设为30。两测点间距为1 579 m,在远震优势频段中1 Hz附近,信号相关性最好,同时噪声相关性接近0。依据信号最大相关和噪声最小相关的原则,台阵最外圆半径应在1 570 m左右。
|
图 6 背景噪声及新不列颠地震P波震相的相干函数 (a)背景噪声相干函数;(b)新不列颠地震P波震相相干函数 Fig.6 Coherence functions of P phase and background noise for the New Britain earthquake |
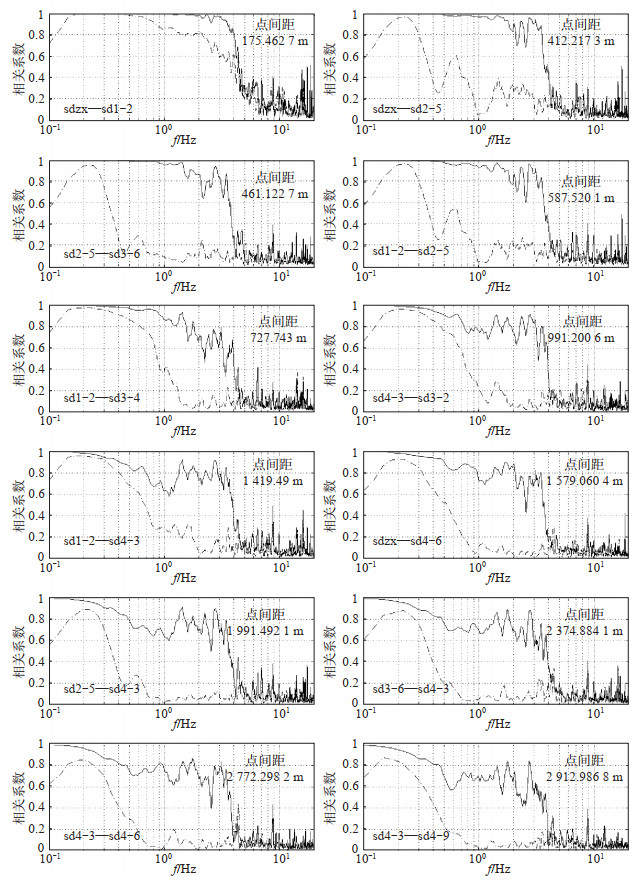
仅计算2个测点之间噪声(信号)相干函数不足以说明问题,故计算所有点两两组合对的相干函数,因篇幅所限,仅列举几幅噪声及信号的相干函数图,结果见图 7,其中测点间距从175 m到2 912 m。
|
图 7 背景噪声及信号的相干函数在不同测点间距的变化 Fig.7 Coherence functions of background noise and signal at different distances between sites |
由图 7可见:①随着两测点距离的增加,信号及噪声的相干函数均随频率增大而逐渐减小;②在相同测点距离,各频段信号相干函数值明显大于噪声相干函数值;③在测点间距为175 m时,噪声相干函数值偏大,而随着距离的增加,该数值逐渐减小,当测点间距为1 579 m时,该数值接近0,此时频率接近1 Hz;④在点间距1 579 m时,在1 Hz频点附近,噪声相干函数接近0,而信号相干函数则大于0.5,信噪比最高。由于远震P波信号频率主要集中在0.8—2.5 Hz,即1 Hz附近,而当点间距为1 579 m,1 Hz(P波信号)对应的信噪比最高,因此台阵监测远震P波信号的最佳距离约1 570 m,与本次台阵勘选的最外圆半径一致。
3.3 三道林场台阵增益根据公式(5),计算得到初选台阵增益,结果见表 3。由表 3可见,Pg震相在1—4 Hz频段增益较高,P震相在0.8—5 Hz频段增益较高。由此可见,该台站可以提高识别Pg和P波震相的能力。但是评估该台阵的地震监测能力,仅计算勘选数据震例增益还不够,需要更多震例予以统计分析(郝春月等,2003)。
| 表 3 P和Pg震相增益 Table 3 The gain of P and Pg phases |
通过对鹤岗三道林场地震台阵背景噪声及信号的相关性分析,得到以下结论。
(1)鹤岗三道林场地震台阵场地背景噪声符合国际监测系统(IMS)的建设标准。其中台阵场地各测点环境地噪声水平(Enl)(sd3-6除外)均达到Ⅰ级,且5 Hz处垂直加速度功率谱均小于-135 dB。
(2)鹤岗地震台阵对于Pg和P波震相识别具有一定增强作用。
(3)该场地对于近震Pg震相的监测,最佳距离在550 m左右,对远震P波信号的监测,最佳距离在1 750 m左右。实际勘选半径从内到外依次为175 m、412 m、823 m、1 587 m,第2个内圆可有效监测近震Pg震相,最外圆可有效监测远震P波震相。因此,近震和远震均在该场地监测范围内,同时反映出鹤岗地震台阵布局设计的合理性。
郝春月, 郑重, 郭燕萍. 中国数字地震台网(CDSN)和IMS/PS台阵的监测定位能力评估[J]. 地震地磁观测与研究, 2006, 27(2): 56-63. |
郝春月, 郑重, 牟磊育. 兰州台阵勘址测点对相干函数的计算与分析[J]. 地震地磁观测与研究, 2002a, 23(4): 29-33. |
郝春月, 郑重, 周公威. 兰州台阵勘址测点的功率谱估计与分析[J]. 地震地磁观测与研究, 2002b, 23(3): 53-58. |
郝春月, 郑重, 周公威. 兰州台阵勘址测点相关值曲线的计算分析与初选台阵评估[J]. 地震学报, 2003, 25(6): 608-614. DOI:10.3321/j.issn:0253-3782.2003.06.006 |
郝春月, 郑重. 信号相关性方法在西藏那曲台阵设计中的应用[J]. 中国地震, 2006, 22(1): 34-42. |
郝春月. IMS的建设背景[J]. 国际地震动态, 2016, 11061106(9): 40-47. DOI:10.3969/j.issn.0235-4975.2016.09.007 |
郑重, 郝春月, 黄昭, 等. 漳州地震台阵背景噪声的特性研究[J]. 中国地震, 2016, 32(3): 454-464. |
郑重, 郝春月, 沙城宁. 格尔木地震台阵勘址数据分析与台阵布局设计[J]. 地震, 2014, 34(2): 13-21. |
郑重, 徐智强. 海拉尔兰州核查地震台阵的勘址和地动噪声功率谱的计算[J]. 地震地磁观测与研究, 2000, 21(6): 11-18. |
 2020, Vol. 41
2020, Vol. 41

