0 引言

烈度计通常布设在土层或结构物上，容易产生放大效应，所测震级值一般较大，若最近台站为烈度计且作为首台触发，其所计算的震级值可能对地震预警震级测定产生较大的影响。为此，以固定测震台网测定的震级为标准，对烈度计震级进行校正。校正后，烈度计震级与测震台网测定的震级趋于一致，可为今后地震预警震级计算奠定基础。

我国地震工作者围绕震级校正、量规函数开展了大量研究，如：李善邦（1981）结合我国常用的短周期地震仪器和基式中长周期地震仪器的特性，得到了量规函数R₁(Δ)和R₂(Δ)，在全国范围内推广使用；陈培善等（1983）研究了云南、四川地区测震台网台站方位、台基及不同测量方法对近震震级的影响，获得较适合该地区测震台站的量规函数和台站校正值；刘瑞丰等(2015, 2017, 2018)利用2002年以前全国各测震台网的大量观测资料，对震级进行深入研究，建立了我国分区地方性震级函数，为新的震级国家标准GB17740—2017做出贡献。针对全国性量规函数，多个省级区域测震台网根据属地化原则开展了更为细致的工作（王丽艳等，2016），如河北、福建、江苏区域测震台网（赵明淳等，2005；林仙坎，2006；康清清等，2019）。以上研究多针对测震台网资料，对于烈度计资料统计比较欠缺。

川滇地区地震频发，平均每年发生1次6级以上地震，3次5级以上地震，为有效监控地震，提高台网密度，增强地震监测能力和预警能力，在该区已布设300多台烈度计。为达到有效进行地震预警的目的，今后将再增加600多台烈度计。由于地震近场记录多数为烈度计台站，而烈度计台站测定震级与测震震级会存在一定偏差，如2017年2月8日云南鲁甸发生M_L 4.9地震，烈度计台站测定的平均震级为M_L 5.2，测震台站与烈度计测定震级偏差为0.3；2018年10月31日四川西昌发生M_L 5.2地震，烈度计台站测定的平均震级为M_L 5.6。因此开展烈度计与测震台网的震级偏差分析与校正的研究工作迫在眉睫，也具有显著的实用价值。本研究借鉴前人在测震台网震级校正的工作，统计烈度计台站的量规函数和台站校正值，获得更适用于川滇地区烈度计地方性震级量规函数和烈度计台站校正值，以提高地震预警系统今后在川滇地区烈度计台站测定震级的精度。

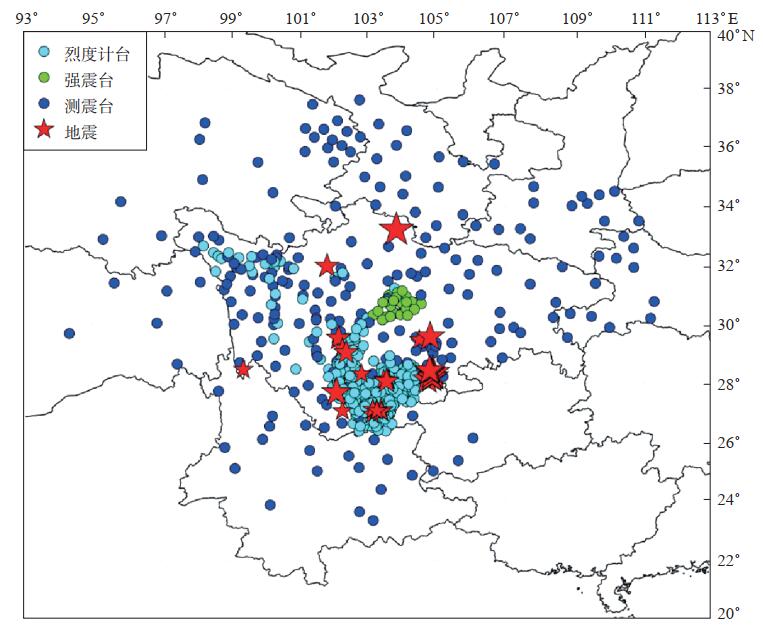
1 资料

收集川滇地区2017—2019年记录的46次M_L 3.0以上地震作为研究资料，其中3.0—4.0级地震23个，4.0—5.0级地震13个，5.0—6.0级地震8个，6.0级以上地震2个（图 1）。川滇地区台站由烈度计台、强震台、测震台组成，共计618个台站，其中烈度计台301个，强震台34个，测震台283个（图 1），重点对烈度计台测定的地方性震级进行校正分析。

如图 1所示，红色五角星表示震例的震中位置，青色实心圆表示烈度计台站，绿色实心圆表示强震台站，蓝色实心圆表示测震台站。

2 数据预处理

如需对测震台网测定震级进行校正，可直接在编目系统导出震相报告予以统计。但对于烈度计测定震级的校正，因烈度计数据未开展日常编目处理工作，则需要对原始资料进行相关处理并人工编目。

烈度计记录的是加速度型数据，而计算地方性震级通常是量取两水平通道位移记录的最大振幅，因此需要将烈度计记录的原始数据进行预处理，主要流程如下：①从原始事件SEED数据格式批量转化成EVT数据格式，便于MATLAB软件读取台站的参数信息（台站名、台站纬度、台站经度、台站仪器响应等）。同时获取台站的波形记录，将波形记录进行基线校正、去仪器响应、加速度仿真位移等处理；②将仿真后的位移记录转化为EVT数据格式，便于使用人机交互处理软件JOPENS-MSDP5.2打开事件波形。人工导入地震到时信息进行初步定位处理，并进行最大振幅的量取工作；③通过事件发生时间，匹配每个事件的地震三要素信息，进而获得每个台站的震中距及测震台网的真实震级值。

据金星等（2005）提出的地动位移仿真方法，将烈度计加速度记录仿真为位移记录，公式如下

$x_{j}=b_{1} x_{j-1}+b_{2} x_{j-2}-S_{0}(\Delta t)^{2}\left[\delta a_{j}+(1-2 \delta) a_{j-1}+\delta a_{j-2}\right]$

(1)

其中

$\left\{ {\begin{array}{*{20}{l}} {{b_1} = 2{{\rm{e}}^{\left({ - \zeta {\omega _0}\Delta t} \right)}}\cos \left[ {{\omega _d}\Delta t} \right]}\\ {{b_2} = - {{\rm{e}}^{\left({ - 2\zeta {\omega _0}\Delta t} \right)}}}\\ {{S_0} = \left({1 - {b_1} - {b_2}} \right)/{{\left({{\omega _0}\Delta t} \right)}^2}}\\ {{\omega _d} = {\omega _0}\sqrt {1 - {\zeta ^2}} } \end{array}} \right.\;\;\;\left\{ {\begin{array}{*{20}{l}} {\delta = {d_1} + {d_2}\left({\Delta t/{T_0}} \right) + {d_3}{{\left({\Delta t/{T_0}} \right)}^2} + {d_4}{{\left({\Delta t/{T_0}} \right)}^3}}\\ {{d_1} = 0.09108}\\ {{d_2} = 0.01945 - 0.04679\zeta }\\ {{d_3} = - 0.00989 + 0.38022\zeta }\\ {{d_4} = 0.50617 - 0.97476\zeta } \end{array}} \right.$

式中，a_j表示j时刻的加速度输入；x_j表示j时刻的位移输出；Δt为采样间隔；ζ表示单自由度系统的阻尼比，通常取0.707；T₀为单自由度系统的自振周期（T₀ = 2π/ω₀），T₀通常取1 s；ω₀表示单自由度系统的自振圆频率。据公式（1），将加速度记录仿真为位移记录，并在位移记录上量取最大振幅，见图 2。

获得每个台站两水平位移记录的最大振幅值，结合台站的震中距信息，利用地方性震级公式，即可计算出每个烈度计台站的实测震级值。公式如下

$M_{\mathrm{L}}=\lg A_{\mu}(\mathit{\Delta})+R(\mathit{\Delta})$

(2)

式中，A_μ(Δ)为地动位移（单位μm），是两水平向最大地动位移的算术平均值；R(Δ)是GB17740—2017《地震震级的规定》附录A——地方性震级量规函数表中的量规函数，按照规定，川滇地区使用R₁₃(Δ)（刘瑞丰等，2017）。

根据式（2），计算所有台站的实测震级值，评估每个台站测定的每个事件的震级值，剔除数据异常的少数台站，确保获得更优数据。

3 震级校正

影响震级测定的因素较多，如各地区的量规函数差异、台站校正值、介质传播方向、台网分布等（李军等，2016）。而本文主要对量规函数和台站校正值两方面进行校正研究，烈度计震级校正公式如下

$M_{\mathrm{L}}=\lg A_{\mu}(\mathit{\Delta})+R_{23}(\mathit{\Delta})+S_{j}$

(3)

式中，R₂₃(Δ)为经过校正后的量规函数；S_j为台站校正值。

3.1 震级偏差统计

对第j个台站，按式（2）求得单台测定第i个地震的震级M_ij，若有N个台站记录到第i个地震且其震级平均值为M_i（陈运泰等，2004），则

$M_{i}=\frac{1}{N} \sum\limits_{j=1}^{N} M_{i j}$

(4)

为了使得烈度计与测震台网震级值一致，将测震台网测定的平均震级值作为M_i，即该地震事件的最终编目M_L。

第i个地震、第j个台站的震级偏差为

$\Delta M_{i j}=M_{i j}-M_{i}$

(5)

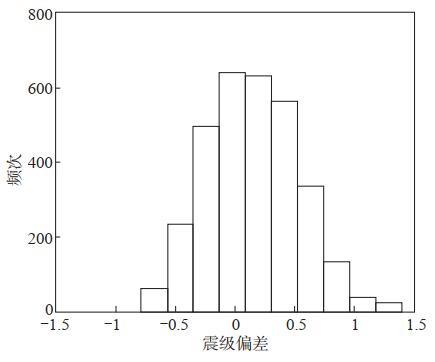
统计得到46个地震事件的3 156条记录，采用式（5），计算各台站震级相对于台网平均震级M_i的偏差，结果见图 3。由图 3可见，震级偏差频次分布规律基本呈正态分布，样本的均值为0.14，样本的标准差为0.38，整体偏大，离散度较大。

3.2 量规函数校正

根据GB17740—2017《地震震级的规定》，云南、四川、重庆、贵州等地的量规函数引用R₁₃(Δ)。本研究在该量规函数基础上进行修正，得到新的量规函数，定义为R₂₃(Δ)。

在利用式（5）计算得到各台站震级偏差基础上，按照原始量规函数R₁₃(Δ)的分段特征，统计震中距各分段范围的震级偏差，分段规则如下：在震中距0—100 km范围内，每隔5 km进行统计；在震中距100—300 km范围内，每隔10 km进行统计。计算各分段的震级偏差平均值 $\overline{\Delta M}_{k}$，公式如下

$\overline{\Delta M}_{k}=\frac{1}{N} \sum\limits_{j=1}^{N} \Delta M_{j}$

(6)

式中，ΔM_j为各分段内的震级偏差，k为分段序号，N为各分段中的样本个数。

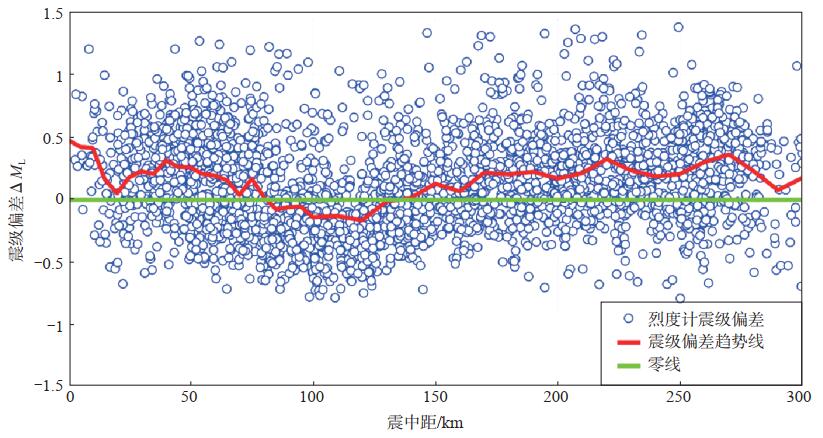
图 4为各台站震级偏差随震中距分布的散点图，将各分段的平均震级偏差连接起来，得到40个点，可见烈度计震级偏差趋势线（图 4中红色线）大部分位于0值以上，说明烈度计测得的震级值普遍偏大。这主要是因为，烈度计通常布设在土层或结构物上，有一定场地放大效应。由图 4可见，在震中距80—130 km范围内，震级偏差呈明显下凹趋势，在震中距120 km附近达最小，此时震级偏差小于0，说明测定震级偏小，可能与受到反射波的影响有关。

在原量规函数R₁₃(Δ)基础上，减去平均震级残差，可获得新的量规函数R₂₃(Δ)，即

$R_{23}(\mathit{\Delta})=R_{13}(\mathit{\Delta})-\overline{\Delta M}_{k}$

(7)

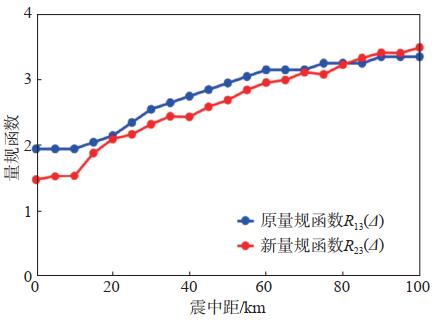
因研究结果主要为地震预警服务，应重点关注震中距100 km范围内的量规函数校正。图 5展示了烈度计测定震级的量规函数R₂₃(Δ)曲线，可以看出，校正后的R₂₃(Δ)绝大部分向下移，由烈度计测得的震级值偏大所致。在震中距0—100 km范围内，统计烈度计震级的新、旧量规函数值，结果见表 1。

将R₂₃(Δ)代入式（2），重新计算各台站震级，根据式（5）重新计算震级偏差，统计其标准差，最终得到R₂₃(Δ)的标准差为0.35，比R₁₃(Δ)的标准差0.38略小，说明校正后的量规函数R₂₃(Δ)更适用于川滇地区。

3.3 台站校正

仪器、台基、放大因子偏差等会造成震级偏差，台站校正即对每个台站的震级偏差进行修正。为了避免量规函数选择不当带来的影响，本研究在新的量规函数修正基础上进行台站校正，针对每个台站，统计其记录的所有地震的震级偏差，计算公式为

$S_{j}=-\frac{1}{N_{\mathrm{e}}} \sum\limits_{i=1}^{N_{\mathrm{e}}}\left(M_{i j}-M_{i}\right)$

(8)

其中，S_j为第j个台站的台站校正值，N_e为第j个台站所记录到的地震个数，M_i为第i个事件的台网平均震级，M_ij为经量规函数修正后的台站震级。

为了保证震级统计的可靠性，只对记录地震数大于10的台站进行校正，经过筛选，得到218个满足要求的烈度计台站。按照台站校正值的大小进行分级评估，其中：台站校正值小于0.1且大于-0.1的定义为小偏差台站，无需台站做台站校正；校正值介于-0.4和-0.1或0.1和0.4的定义为中等偏差台站，原则上需要进行台站校正；台站校正值大于0.4或小于-0.4的定义为大偏差台站，需要重点注意，必须进行台站校正。据以上原则，得到73个小偏差台站，13个大偏差台站，132个中等偏差台站。台站校正值较大的烈度计台需要重点关注，特别是当这些台站被用作地震预警的首台震级估算时。表 2列出13个此类台站，可见YN.C0207烈度计台站校正值最大，为-0.55。

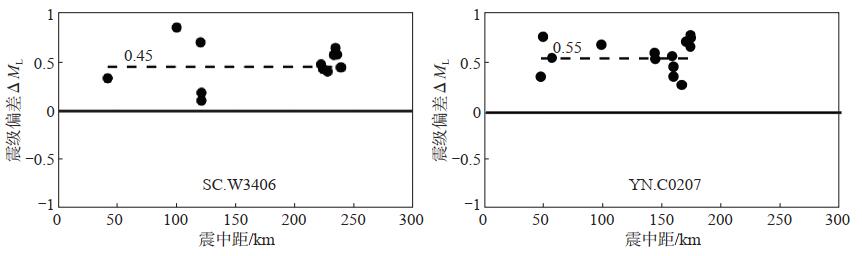
SC.W3406台和YN.C0207台校正值较大，以2个台站为例，给出其烈度计震级偏差分布，结果见图 6。由图 6可见：四川烈度计W3406共记录到16个地震记录，震级偏差均偏大，平均震级偏差为0.45，因此其台站校正值为-0.45；云南烈度计C0207共记录到15个地震记录，震级偏差均偏大，平均震级偏差为0.55，因此其台站校正值为-0.55。

4 校正结果分析

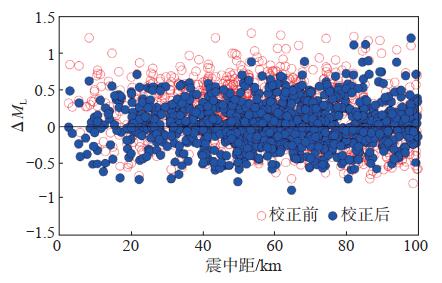
经量规函数修正和台站校正后，利用式（3），对研究所用的3 156条记录，重新计算各烈度计台的震级值，并与校正前的震级值进行对比。为了估算地震预警震级，重点选取震中距100 km范围内的烈度计台，统计对比震级校正前后震级偏差的均值和标准差，结果见图 7，图中红色空心圆为校正前的震级偏差，蓝色实心圆为校正后的震级偏差。由图 7可见，校正后震级偏差更加聚拢，偏差均值由校正前的0.145降低到0.033，从整体偏大降低到0值上下波动；标准差由0.382降低到0.295，离散度减小，震级校正后的结果更优。

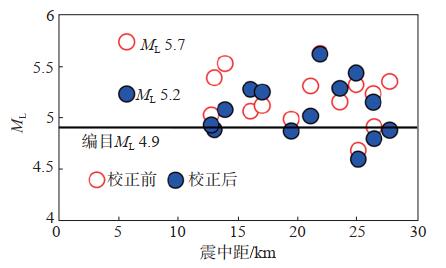
2017年2月8日云南昭通鲁甸发生M_L 4.9地震，震中距约5 km的烈度计台测得震级为M_L 5.7，可看作烈度计首台记录，与测震台网测定震级偏差达0.8。利用新的量规函数R₂₃(Δ)和台站校正值，对震中距30 km范围内烈度计台测定震级进行校正，校正前后震级分布见图 8。由图 8可见，首台烈度计测定震级值由M_L 5.7降低至M_L 5.2，震级偏差由0.8降至0.3。统计发现，该震级范围内各烈度计台所测平均震级值由M_L 5.2降低至M_L 5.0，更加接近地震编目给定的震级值M_L 4.9。可见，利用新的量规函数R₂₃(Δ)和台站校正值进行校正，可有效提高震中距较近的烈度计台震级估算精度。

5 结论

地震预警震级的测定，通常关注近场前几台的震级测定结果，而近场多为烈度计台，确保其震级测定精度至关重要。通过对烈度计台震级残差的分析，获得适用于川滇台网的量规函数和台站校正值，不仅可减小震级离散度，而且对地震预警的首台震级测定具有较高的应用价值。

（1）对烈度计台与编目震级的偏差进行统计，发现：烈度计台测定震级值总体偏大约0.2；在震中距80—130 km范围内，烈度计台测定震级偏小。采用新量规函数R₂₃(Δ)求得的震级偏差的标准差为0.35，比利用R₁₃(Δ)所得结果（0.38）略小，说明R₂₃(Δ)更适用于川滇地区烈度计台的震级估算。

（2）按照台站校正值大小，把川滇地区烈度计台分为3个等级，即：台站校正值小于0.1、大于-0.1的73个小偏差台站，无需进行震级校正；台站校正值大于0.4或小于-0.4的13个大偏差台，需重点关注，其中云南C0207烈度计台震级偏差最大，台站校正值为-0.55；台站校正值介于-0.4和-0.1之间或0.1和0.4之间的132个中等偏差台站，原则上进行适当校正。

（3）经量规函数修正和台站校正后，烈度计测定震级的偏差均值由校正前的0.145降低到0.033，由整体偏大降低到在0值附近波动；标准差由0.382降低到0.295，离散度减小，震级校正后结果更优。修正后的量规函数和台站校正值更加适用于川滇地区烈度计台站的震级计算，可为今后地震预警烈度计震级测定提供参考。

6 结束语

针对烈度计台站开展震级校正工作，在测震台网量规函数基础上，得到适用于烈度计的新量规函数。另外，对每台烈度计进行台站校正，获得偏差较大台站的校正值。比较烈度计台测定震级校正前后的结果，可知校正结果明显优于校正前，提高了近场烈度计震级的可靠度和准确性。

本研究所选震例资料有限，限于每个台站至少提供10条地震记录的要求，文中仅给出218个烈度计台站的校正值，今后将进一步增加震例资料，并纳入未来拟扩建的烈度计台，以获得更加适合且可靠的量规函数和台站校正值，完善此项工作，为地震预警服务。

四川省地震局监测中心提供烈度计数据，编辑部及审稿专家对论文撰写提出宝贵意见，在此表示感谢。