0 引言

在地震监测能力薄弱地区，因存在固定台站较稀疏、地震事件震级较小等问题，会造成地震目录的严重缺失，这对于研究诸如地震活动构造、地球内部结构、震源的几何构造等地震学基本问题带来了较大困难(侯金欣，2016)。多年来，提高监测能力薄弱区拾震能力的研究一直受到广泛关注。

近年来，许多深度学习方法被应用到震相自动拾取领域，如卷积神经网络CNN(convolutional neural network)(Perol et al，2018；Ross et al，2018；于子叶等，2018；Zhu et al，2019b；赵明等，2019a)、递归神经网络RNN(recurrent neural network)(Zhou et al，2019)、全连接神经网络FCN(fully convolutional network)(Woollan et al，2019)和U形网络U-Net(Zhu et al，2019b；赵明等，2019b)。

Zhu等(2019a)首次将U-net应用于震相拾取，提出了PhaseNet方法，并取得较好的效果。但是，PhaseNet方法在设计和训练过程中都是以事件为核心的，应用于连续波形上进行震相识别时有一定的困难。赵明等(2019b)尝试将与PhaseNet类似的U-Net震相拾取模型用于连续波形，得到了初步结果，但仍然被实际数据中复杂的噪声所困扰(刘芳等，2020)，仍需改进。

结合波形互相关技术的双差层析定位方法(tomoDD)是一种较有发展前景的方法。它是针对如何分别克服“地震精度不高”2方面误差源而设计的一种定位方法(Zhang et al，2003)。波形互相关技术的使用可以使某些震相到时读数精度高达7‰s；而相对走时差的使用很大程度上解决了传统方法中因速度结构不够准确而造成的地震定位矢量分散问题，可使定位精度高达几十米甚至几米(王雨，2019)。

本文采用结合台阵策略的震相拾取深度学习方法APP(刘芳等，2020)，基于中国地震科学台阵资料(简称喜马拉雅台阵)及内蒙古、甘肃地震台网波形资料，针对内蒙古阿拉善右旗(38°—43°N，96°—105°E)地震监测能力薄弱的现状(只有EKH、WLJ、CEK等3个地震台)，开展提升研究区监测水平研究，并使用双差层析定位方法(tomoDD)探测地震并精确定位，以增强固定台网的微震识别能力，以期提高监测能力薄弱地区的地震监测水平。

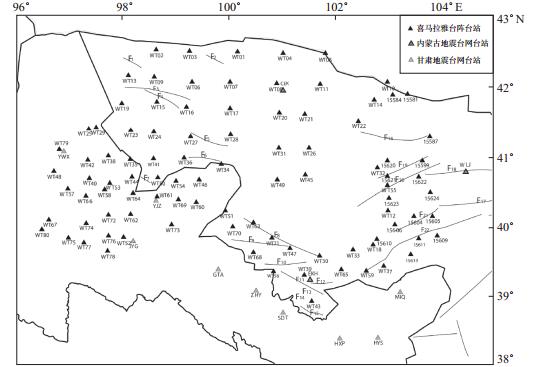
1 资料的选取

依托喜马拉雅台阵资料，选取2014年1月—2015年10月110个台站(喜马拉雅台阵有96个、甘肃地震台网有11个，内蒙古地震台网有3个)的连续波形资料(图 1)，并作如下预处理。

(1) APP方法。去均值，去斜率，重采样至50 Hz，butterworth取4阶滤波2—15 Hz。

(2) 弱模板识别。去均值，去趋势，去仪器响应；频谱分析及滤波；模板事件的获取等。

2 APP方法和双差层析定位方法的原理

本文针对研究区，采用结合台阵策略的震相拾取深度学习方法APP进行自动拾取地震(刘芳等，2020)，并将拾取的地震进行双差层析定位方法(tomoDD)精确定位。

2.1 结合台阵策略的震相拾取深度学习方法APP

APP方法从网络结构、样本集构造等方面对U-net型的震相拾取模型进行改进，设计了震相拾取模型PP(Phase Picker)，并将该网络和所提出的台阵策略相结合(蒋一然等，2019)，形成了震相拾取方法APP(刘芳等，2020)。

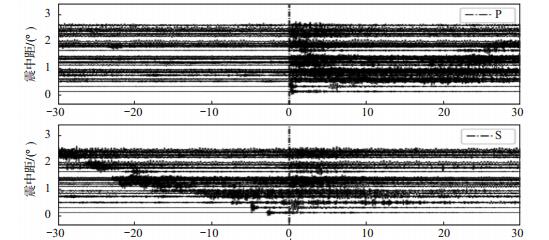
为了使模型能够更好地满足扫描连续波形的需求，并适用于更多的地震资料，建立了2个模型(即PP模型)(图 2)，分别对P波和S波进行识别。图 3给出了P波和S波按拾取到时对齐并以台站震中距排列的例子。

增加有震相部分的权重以均衡样本，得到如下的损失函数F(x)

$ F\left(x \right){\text{ = - }}{\Sigma _x}{w_0} \times p\left(x \right) \times \lg q\left(x \right) + {w_1}\left[ {1 - p\left(x \right)} \right] \times \lg \left[ {1 - q\left(x \right)} \right] $

(1)

其中，p(x)为真实概率分布；q(x)为震相类型概率；w₀和w₁分别为震相和噪音的权重。

将PP模型与蒋一然等(2019)的“以P、S震相到时差作为时空约束的台阵策略”相结合，形成了APP拾取方法。具体拾取流程如下。

(1) 使用训练好的PP模型的2个网络，对三分量数据进行滑动扫描，分别识别P波和S波，取输出结果大于0.5的峰出现的位置作为P波、S波的到时。时间窗每次滑动10 s，P波取每个时间窗中15—25 s时间段的输出结果，S波取20—30 s时间段的输出结果。

(2) 寻找同一台站上到时差小于80 s的P、S震相，并根据到时差估算发震时刻和台站与震中间的距离。

(3) 根据台阵策略，将研究区域划分为多个子区域，联合不同台站的估计结果，取发震时刻和震中位置一致性最好的时刻和子区域作为发震时刻和震中位置。

(4) 将不同台站满足发震时刻和震中位置的拾取结果与相应的地震匹配起来，剔除未被匹配的震相，得到最终的地震和震相到时目录。

2.2 tomoDD方法

根据射线理论，从地震的震源到台站k，体波走时T(Zhang et al，2006)为

$ T_k^j = {\tau ^i} + \smallint _i^ku{\text{d}}s $

(2)

其中，τⁱ为事件的初始时刻；u为慢度场；d为路径长度。震源点坐标(x, y, z)、事件初始时刻、慢度场、射线路径都是未知的，由式(2)可知，积分在慢度上是线性的，而在震源坐标上为非线性，故速度结构收敛快于地震定位。式(2)走时方程为非线性，故使用截断泰勒级数展开使之线性化，将观测走时和预计走时之差r_kⁱ与震源、速度模型扰动联系起来(Zhang et al，2006)，则有

$ r_k^i = \sum\limits_{l = 1}^3 {\frac{{\partial T_k^i}}{{\partial x_l^i}}\Delta x_l^i + \Delta } {\tau ^i} + \smallint _i^k\delta u{\text{d}}s $

(3)

对于同一台站观测到的事件，其线性化方程如下(Zhang et al，2006)

$ r_k^j = \sum\limits_{l = 1}^3 {\frac{{\partial T_k^j}}{{\partial x_l^j}}\Delta x_l^j + \Delta } {\tau ^j} + \smallint _j^k\delta u{\text{d}}s $

(4)

将式(3)、(4)相减，得到(Zhang et al，2006)

$ r_k^i - r_k^j = \sum\limits_{l = 1}^3 {\frac{{\partial T_k^i}}{{\partial x_l^i}}\Delta x_l^i + \Delta } {\tau ^i} + \smallint _i^k\delta u{\text{d}}s - \sum\limits_{l = 1}^3 {\frac{{\partial T_k^j}}{{\partial x_l^j}} - \Delta } {\tau ^j} - \smallint _j^k\delta u{\text{d}}s $

(5)

假设i、j两事件震源相距足够近，则从2个事件震源到同一台站的路径近乎一致，式(5)可化简为(Zhang et al，2006)

$ {\text{d}}r_k^{ij} = r_k^i - r_k^j = \sum\limits_{l = 1}^3 {\frac{{\partial T_k^i}}{{\partial x_l^i}}\Delta x_l^i + \Delta } {\tau ^i} - \sum\limits_{l = 1}^3 {\frac{{\partial T_k^j}}{{\partial x_l^j}} - \Delta } {\tau ^j} $

(6)

其中，dr_k^ij即为双差——2个事件微分到时的观测值和理论值之差(Zhang et al，2006)。

$ {\text{d}}r_k^{ij} = r_k^i - r_k^j = {\left({T_k^i - T_k^j} \right)^{{\text{obs}}}} - {\left({T_k^i - T_k^j} \right)^{{\text{cal}}}} $

(7)

观测的微分到时(T_kⁱ-T_k^j)^obs可由波形互相关和绝对目录到时计算得到。

我们也可以用三维网格将速度模型离散化，式(3)可写作(Zhang et al，2006)

$ r_k^i = \sum\limits_{l = 1}^3 {\frac{{\partial T_k^i}}{{\partial x_l^i}}\Delta x_l^i + \Delta } {\tau ^i} + \sum\limits_{m = 1}^{{M_{ik}}} {} \sum\limits_{n = 1}^N {{w_{mn}}} \Delta {u_n}\Delta {s_m} $

(8)

3 APP方法与人工拾取地震结果分析 3.1 APP与台网人工拾取结果对比分析

利用APP方法共识别地震32 830次，固定台网人工拾取地震1 462次。图 4为APP方法和固定台网拾取地震的分布。由图 4可见，研究区域的东部、南部、西部有较多断层，APP方法检测到的地震基本沿断层展布。北部断层较少，但也观测到了一些地震，它们集中分布于海拔较低的隆起处。拾取结果反映了该地区地震活动性的空间变化。

台网人工拾取的1 462次地震，主要是依靠甘肃地震台网的记录进行定位的。这些地震主要分布于南部断层较多的区域，因该区域台站分布稀疏，故对地震的检测能力较弱。

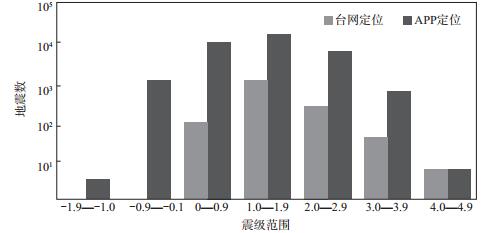
将APP方法自动拾取到的32 830次地震与人工拾取的1 462次地震进行匹配，APP方法找到了台网人工拾取的1 406次地震，召回率为96.7%，拾取总数为人工目录数的22倍。通过对计算结果分析(图 5)，针对M_L -1.9— -1.0和M_L-0.9— -0.1两个震级档，台网人工拾取地震比例为0，APP方法拾取比例为3.44%。可见，APP方法在拾取微小地震方面占有一定的优势，APP方法地震检测能力为0—1.9级，人工拾取的地震检测能力为1.0—1.9级，且在0级以下无检测能力。可见，APP自动拾取方法将台网的地震检测能力提高了1.0级左右。

3.2 tomoDD方法定位结果 3.2.1 数据预处理及tomoDD方法定位

从利用APP方法获得的32 830次地震中选取到时拟合误差小、至少被5个台记录到、到时拟合的残差小于3 s的高精度地震11 165次。

基于11 165个高精度地震，选取震中距小于200 km、信噪比大于3的台站到时数据，且要求地震至少被5个台记录到，到时拟合误差小于2 s，地震对最大距离0.3°，震相波形互相关系数大于0.75，每个地震的震相对数目不超过400个。在上述设定条件下，筛选到5 593次地震，经过tomoDD方法定位，得到了5 542次定位地震(图 6)。

3.2.2 tomoDD方法定位前后深度对比

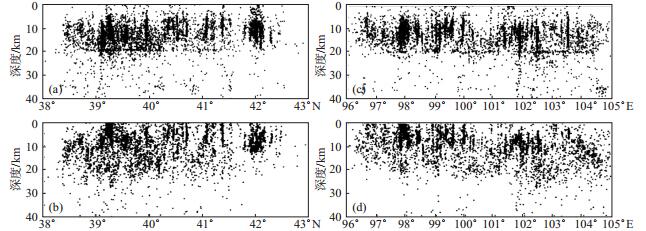
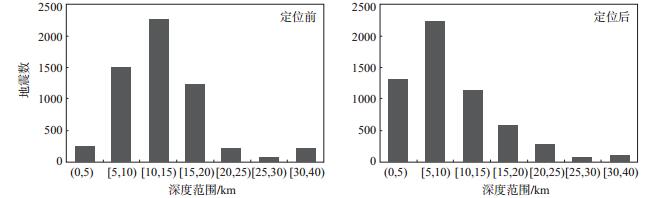
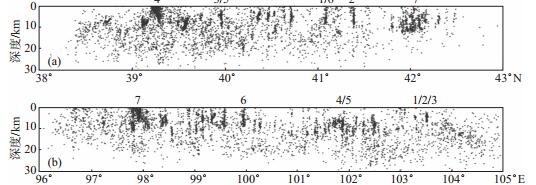
从定位前后地震深度分布以及数据统计结果可知(图 7，图 8)，定位前，87%的地震震源深度为5—20 km，在20 km处有一个较明显的分界线，均值为13.6 km，且分布形态呈“竖条状”，只有少数地震震源深度大于20 km。经过tomoDD方法定位后，97.2%的地震震源深度为0—30 km，均值为9.9 km，该结果与刘芳确定的内蒙古地区一维速度模型中上地壳厚度为30 km的结果较接近，因此利用tomoDD方法定位后地震震源深度分布较符合内蒙古西部地区的地质构造特征。

3.2.3 tomoDD方法定位深度与断裂对应关系初步分析

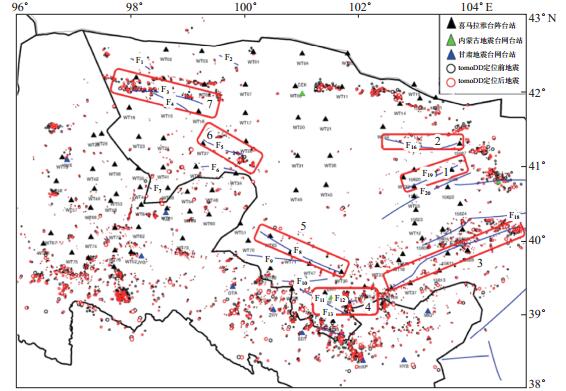
地震震源深度是探讨地震孕育和发生的深部环境、地壳变形及其力学性质和属性以及圈层构造等诸多大陆动力学问题的重要参数。目前，对于阿拉善地区的断层构造探测研究结果较少，邓起东(2000)充分整理了中国大陆分布活动断裂、地震地表破裂带、活动褶皱、活动盆地、火山活动、活动块体与地震、活动构造间的关系等资料，其中包含了研究区所在的内蒙古西部活动断裂数据，本文使用上述数据绘制研究区活动断层分布图，开展震源深度与断裂位置间相关性的初步分析(图 9，图 10，表 1)。

从图 9可知，研究区共有17条断裂带。由图 10(a)、图 10(b)可见，地震频发地区震源深度随纬度和经度呈密集条带分布，通过对比地震频发地区所对应的经纬度位置与研究区断裂带分布，对照发现地震频发地区与断裂带位置分布间存在对应关系。深度随纬度变化中有5条“集中条带”与研究区7条断裂的纬度位置相对应[图 10(a)]，深度随经度变化中有4条“集中条带”与研究区7条断裂的经度位置相对应[图 10(b)]。在图 9中用红框分别对这7条断裂位置进行了标注，标注序号与图 10(a)、图 10(b)所对应的经纬度位置序号基本一致，对应的断裂分别为：F₁₉宗乃山断裂、F₁₆希热哈达断裂、F₂₂雅布赖山南麓断裂、F₁₂阿拉善右旗断裂、F₈北大山北缘断裂、F₅龙峰山北侧断裂、F₃甜水井南断裂和F₄仙人岛西断裂(表 1)。

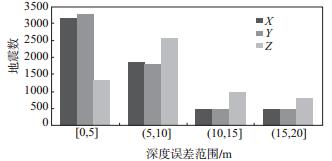
3.2.4 tomoDD方法定位的误差分析

通过tomoDD方法定位，得到了5 542次地震轴、轴、轴的定位误差分布(图 11)。由图 11可知，轴误差为0.20—36.20 m，均值为5.54 m；轴误差为0.30—32.70 m，均值为5.45 m；轴误差为0.20—54.30 m，均值为9.34 m。

4 结论与认识

通过对内蒙古地震监测薄弱区拾震能力的研究，得到如下结论。

结合PP模型和台阵策略的震相拾取方法APP，具有在实际连续波形上准确识别地震和精确提取震相到时的能力, 可提供高精度的地震目录和震相到时数据，在本文实际地震资料应用中展示出较强的泛化能力，该方法可直接用于台阵资料。

(2) 基于研究区喜马拉雅台阵数据进行地震事件拾取，选取2014年1月—2015年10月110个台站(喜马拉雅台阵96个、甘肃地震台网11个，内蒙古地震台网3个)的连续波形资料，采用APP方法共拾取到32 830个地震；在相同区域相同时段由内蒙古测震台网人工浏览拾取台网14个固定台站(甘肃地震台网11个，内蒙古地震台网3个)的连续波形资料，共拾取到1 462个地震。将2个地震目录进行匹配对比，APP自动拾取方法召回率为96.7%，拾取总数为人工目录数的22倍。通过对计算结果进行分析认为，APP方法对于研究区微震具有较强的识别能力，而人工拾取由于台网台站分布较稀疏，故对微小地震监测能力弱；APP方法使用喜马拉雅台阵的数据，相比台网人工拾取的地震监测能力提高了1级左右，为下一步台网优化布局、提高监测能力提供了参考依据。

(3) 经tomoDD方法定位后，震源深度为0—30 km，深度分布较符合内蒙古西部的地质构造特征。

(4) 对震源深度与断裂位置间相关性的初步分析结果显示，深度随纬度变化中有5条深度“集中条带”与研究区7条断裂的位置相对应，深度随经度变化中有4条深度“集中条带”与研究区7条断裂的位置相对应。

(5) 分析tomoDD方法定位误差可知，轴、轴和轴误差均值分别为5.54 m、5.45 m、9.34 m。均在误差允许范围之内。

中国地震科学台阵探测计划提供地震资料，北京大学宁杰远教授、中国科学技术大学张海江教授指导给予，在此表示感谢。