衡量地震大小的一个基本参数是震级。震级参数的精确度不仅影响监测速报工作,也是地震研究、地震预测、抗震应急救灾及灾后评估等方面的重要依据(许德相等,2015),因此,缩小单台震级偏差具有重要意义。
震级测定结果受量规函数、台基岩性、仪器等方面的影响,存在一定的误差。由于影响因素的多样性及不确定性,如何准确测定震级成为一个复杂的科学问题。近年,一些研究者(陈继锋等,2013;万玉杰等,2014;吕作勇等,2015;项月文等,2018)针对甘肃、青海、广东、江西等测震台网开展了量规函数影响地方性震级偏差的研究。詹小艳等(2010)、王鑫等(2015)针对江苏、内蒙古等测震台网子台进行了地方性震级偏差研究。自2001年10月数字化之后,河北测震台网记录了大量的地震数据,有关河北测震台网台基、仪器、测量方法等方面的研究已有报道(李雪英等,2004;张从珍等,2004;赵明淳等,2005)。随着“十五”数字化地震观测网络项目及其他后续项目的开展,河北省台站数量增加,仪器的更换及定位精度要求的提高,使得目前所使用的地方性震级量规函数不能很好地满足要求。本文利用现有的资料数据综合分析多个影响因素,试图从中找出影响误差的主要因素并进行必要修正,以期为进一步提高河北测震台网地震震级测定结果精度提供帮助。
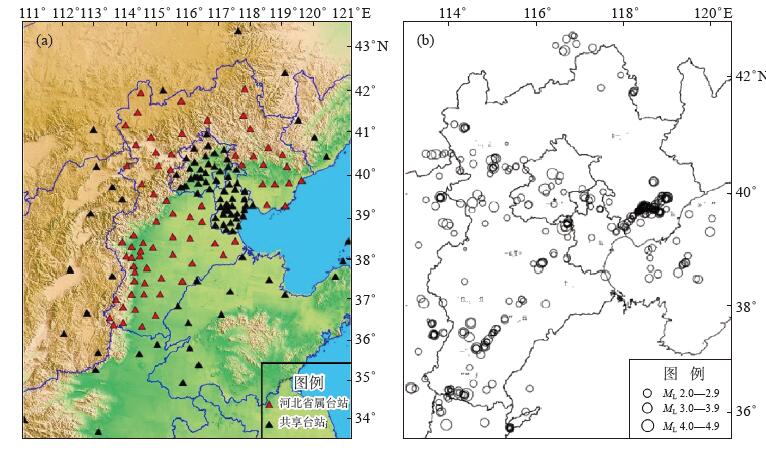
1 台网概况及资料选取2017年12月15日后,河北测震台网共接收168个地震台站的数据,河北省台站71个,邻省共享台站97个。其中共享台站中,北京台站28个,天津台站31个,中国地震局地球物理研究所台站1个,内蒙古台站4个,辽宁台站5个,山西台站9个,河南台站5个,山东台站14个。
河北71个台站中,地表台站共47个,其中,使用地面甚宽频带地震计的台站6个,使用3ESPC-60三分量宽频带地震计的台站10个,使用BBVS-60宽频带地震计的台站31个;井下台站共24个,其中,使用FSS-3DBH地震计的台站22个,使用BBVS-60DBH宽频带的台站2个,台站分布见图 1。
|
图 1 河北测震台网168个接收台站及所选地震事件震中分布 (a)台站分布;(b)震中分布 Fig.1 Distribution of seismic stations (168) in the Hebei Seismic Network and epicenters of selected earthquakes |
本文选取2017年12月至2019年8月河北测震台网记录的河北及周边地区(省行政边界线外30 km内,含北京市和天津市)330次ML≥2.0地震事件,采用数据处理软件JOPENS-MSDP,定位方法均为单纯性定位,振幅量取的前提是仿真成W-A(伍德-安德森),并且振幅取值为S波在NS、EW方向上的最大振幅。依据此方法求得71个子台的震级与平均震级,对所得数据资料进行统计分析,所选地震事件震中分布见图 1。
2 计算方法目前,河北测震台网各台站均采用数字化速度型记录,震级主要依据S/Lg上最大振幅值测定,公式为
| $ {M_{\rm{L}}} = \lg {A_{\rm{ \mathsf{ μ} }}} + R(\varDelta) $ | (1) |
式中,Aμ为以μm为单位的地动位移,Aμ = (AN + AE)/2,其中,NS、EW分向的S波(或Lg波)位移最大振幅分别为AN、AE;Δ为震中距;R(Δ)为量规函数(表 1)。
| 表 1 量规函数 R(Δ) Table 1 Calibration functions R(Δ) |
假设地震事件数为P,记录到每个地震事件的台站数为K,由式(1)得到第n个地震事件第m个单台震级MLnm,依据每个地震事件的震级由下式得到第n个事件的台网平均震级MLn
| $ {M_{{\rm{L}}n}} = \frac{1}{K}\sum\limits_{n = 1}^K {{M_{{\rm{L}}nm}}} $ | (2) |
根据下式,便可得到第n个地震事件的第m个子台震级偏差值ΔMLnm
| $ \Delta {M_{{\rm{L}}nm}} = {M_{{\rm{L}}nm}} - {M_{{\rm{L}}n}} $ | (3) |
最后,利用下式分别计算第m个子台所记录的地震事件的单台震级平均偏差ΔMLm及标准偏差δm
| $ \Delta {M_{{\rm{L}}n}} = \frac{1}{P}\sum\limits_{m = 1}^P {({M_{{\rm{L}}nm}} - } {M_{{\rm{L}}n}}) $ | (4) |
| $ {\delta _m} = \sqrt {\frac{{\sum\limits_{m = 1}^P {{{({M_{{\rm{L}}nm}} - {M_{{\rm{L}}n}})}^2}} }}{{P - 1}}} $ | (5) |
本文采用上述的计算方法将选取330个地震事件的8 053个单台记录的地震数据统计分析,计算出71个单台震级相对于台网平均震级的平均偏差ΔMLm以及标准偏差δm,结果可见表 2。由表 2可见,每个单台测定的震级都存在不同程度的偏差,平均偏差为-0.32—0.78,河北台网测定的震级为量规函数校正后的结果,因此统计数据可以直观地对现使用的量规函数校正效果作一定的评估。根据统计结果,8 053个记录中误差绝对值|ΔMLnm|≤0.2的比例为58.3%,其中,13个单台的偏差绝对值大于0.2,正定南台偏差绝对值达到0.78,说明虽然旧量规函数的校正效果是显著的,但是对于近几年更换仪器的或重新添加的单台进行重新校正是必要的。
| 表 2 各个单台震级平均偏差及标准偏差统计 Table 2 Statistics of average deviations and standard deviations of single station magnitudes at each seismic station |
71个单台震级的标准偏差为0.08—0.41,整体浮动不大,大于0.30的只有8个台,占所有单台的11.3%,表明单台震级的偏差离散程度不大。
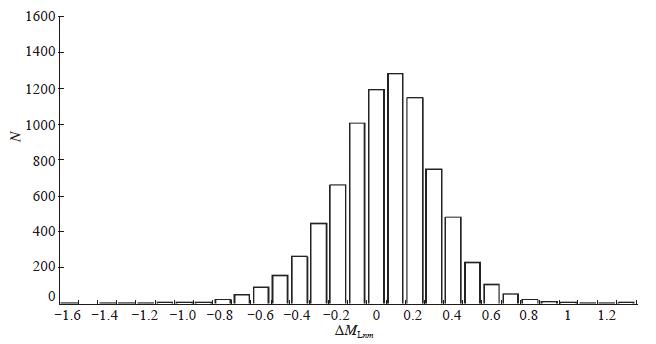
71个单台8 053个记录的偏差 ΔMLnm 频次分布如图 2所示。由表 2也可计算得到 |ΔMLnm |≤0.2的记录4 692个;0.2<|ΔMLnm|≤0.4的2 311个;0.4<|ΔMLnm|≤0.6的742个;0.6<|ΔMLnm|≤0.8的217个;|ΔMLnm|>0.8的93个。总体来说,震级偏差较符合正态分布,这也进一步说明震级偏差离散程度不大。
|
图 2 原始震级偏差统计 Fig.2 Statistics of original magnitude deviations |
由式(1)可知,量规函数是地方性震级测量中沿着传播路径振幅产生衰减变化的补偿值,即对地震波区域性衰减特征的定量描述,也与区域的地壳结构有着密切关系(陈培善等,1983),所以量规函数R(Δ)的精确度直接影响震级的精确性。
本文选取的数据资料震中距范围为0—683 km,其中,99 %的震中距小于460 km,震中距大于460 km的仅有56个,因此将震中距小于460 km的以10 km为间隔划分为46个区域段,由下式计算每段的单台震级偏差的平均值
| $ \overline {\Delta {M_b}} = \frac{1}{N}\sum\limits_j^N {\Delta {M_j}} $ | (6) |
式中,b为间隔数;N为间隔范围内震级偏差样本数,结果见表 3、图 3。
| 表 3 按震中距分段统计震级平均偏差 Table 3 Statistics of average deviations of magnitude with respect to epicenter distance |
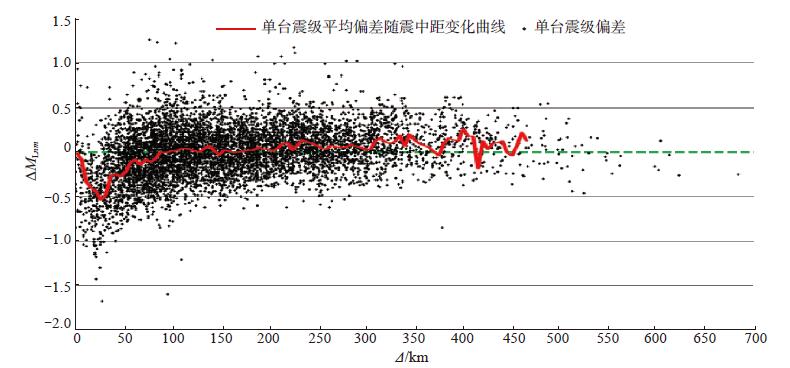
|
图 3 单台震级偏差随震中距的变化 Fig.3 Variation of deviations of single station magnitude with epicentral distance |
由表 3、图 3可见:①震中距为0—80 km时,单台震级平均偏差小于0,尤其是震中距小于50 km时平均偏差均小于-0.20,偏差绝对值较大且波动较大,说明在此震中距范围内量规函数值偏小,稳定性较低,需要取表 3中相对应的平均偏差的负数进行修正;②震中距为80—300 km时,除最大平均偏差0.11以外,其余的绝对值都小于0.08,说明量规函数较适用,此震中距范围内的便不需要进行校正;③震中距大于300 km时,平均偏差既有正值也有负值,并且波动较大,说明此范围的量规函数不稳定,可细分为以下几个震中距范围:震中距为300—350 km、370—405 km、410—435 km、450—460 km时,平均偏差均大于0.1,说明此范围内的量规函数整体偏大;震中距为350—370 km时,平均偏差绝对值小于0.1,但是正负值均有,波动较大;震中距为435—440 km时,平均偏差为0,说明此区间量规函数非常吻合;其余震中距区间内的误差值小于0。因此,震中距在300—460 km范围内取负值,作为校正值进行量规函数校正。
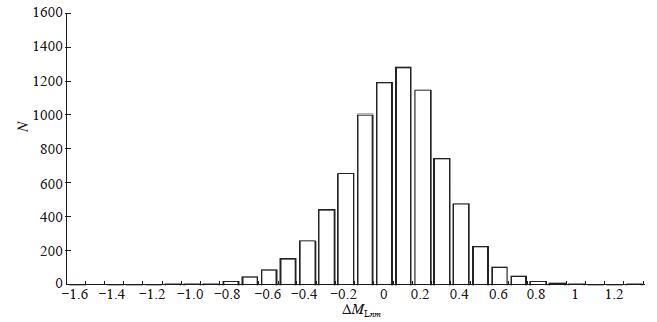
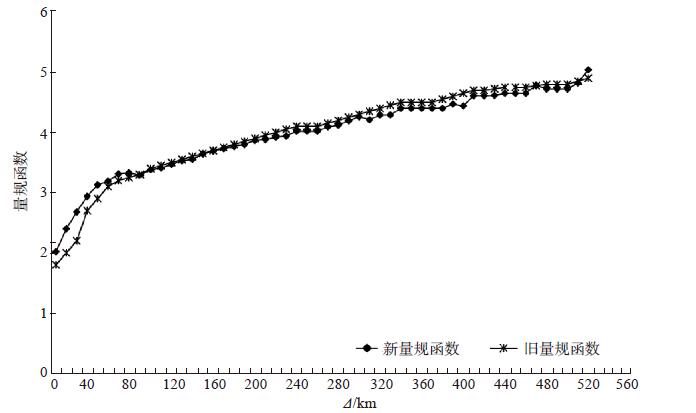
取表 3中平均偏差的负值对旧量规函数进行修正,根据新的量规函数重新计算71个单台测定的震级相对于台网平均震级的平均偏差及标准偏差,结果如表 4所示,校正后单台偏差ΔMLnm频次分布见图 4。另外,对于震中距小于80 km及震中距为300—460 km的台站,进行震级修正后得到河北地区的新量规函数(图 5)。
| 表 4 量规函数校正后各个单台震级平均偏差及标准偏差统计 Table 4 Statistics of average deviations and standard deviations of single station magnitudes at each seismic station after correction using the calibration function |
|
图 4 量规函数校正后震级偏差统计 Fig.4 Statistics of magnitude deviations after correction using the calibration function |
|
图 5 新旧量规函数的对比 Fig.5 Comparison of old and new calibration functions |
比较表 2和表 4可知:经过量规函数校正后,71个单台中32个台站的震级偏差明显地降低,29个台站稍有上升,10个台站没有变化,其中,陡河台、京唐港台、涉县台、围场台、红山台、沽源台的震级偏差明显下降,说明这些台站受量规函数的影响较大。校正前标准偏差为0.08—0.41;校正后为0.15—0.39,除6个台站不变及11个台站略微上升以外,其余台站均明显下降,对比图 2和图 4更能说明量规函数校正后震级偏差整体明显收敛。
3.3 台基的影响河北测震台网71个台站分为地表型基岩台站和井下型土层台站2大类,即对于基岩类型,台站建在地表;而土层类型,台站建在井下。地表型台站47个,井下型台站24个,表 5为地表型基岩、井下型土层台站震级平均偏差及标准偏差。由表 5可见,地表基岩型台站平均偏差略小于井下型土层台站,但二者整体绝对值都不大,校正前后平均偏差绝对值变化不大,表明台站建在地表与井下、基岩与土层对震级偏差的影响不大。
| 表 5 地表型基岩、井下型土层台站震级平均偏差及标准偏差 Table 5 Average magnitude deviations and standard deviations for seismic stations with a base of the subsurface rock and underground soil layer |
河北测震台网71个台站的台基岩性有所不同,地震波在不同台基岩性中传播的衰减系数有很大差异,若台基岩性质地松散,对震级会产生放大作用;而相对质地坚硬、结构致密的台基对震级会产生缩小的影响。针对量规函数校正后的71个台站,重新计算了各个台的震级平均偏差(表 4)。由表 4可见,经量规函数校正后蠡县台、鹿泉台、秋树坪台、雄县台、元氏台、枣强台、正定南台、逐鹿台、遵化台震级平均偏差无变化,说明其震级偏差不受量规函数的影响,这可能主要与台站的台基岩性有关,因此进行台基校正。另外,进行量规函数校正后昌黎台、岗南台、沽源台、怀安台、临城台、临漳台、孟村台、无极台单台震级平均偏差绝对值仍大于0.2,这说明仅仅进行量规函数的校正对于缩小台站的震级偏差并没有良好效果,这些台站可能受量规函数及台站台基岩性的双重影响,因此需要在量规函数校正后进行台基校正。对于需校正的台站取其量规函数校正后平均偏差(表 4中平均偏差列的值)的负值作为台基校正值。
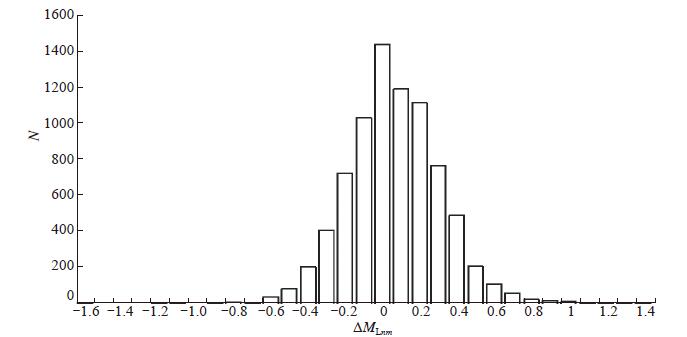
经台基校正后的71个单台震级偏差的频次分布如图 6所示。由图 6可见,与量规函数校正后相比,正态分布更集中收敛,震级偏差|ΔMLnm|≤0.2的由4 921次增至为5 083次,占比提高至63.12%,说明对量规函数校正后震级偏差仍很大或震级偏差无变化的台站进行台基校有一定必要性。
|
图 6 台基校正后的震级偏差 Fig.6 Magnitude deviations after lithologic calibration |
为了对仪器类型的影响作进一步讨论,按地震计类型将71个台站归为6类,详见表 6、表 7。
| 表 6 各个单台震级偏差、标准偏差及仪器类型 Table 6 Magnitude deviation, standard deviation, and instrument type for each station |
| 表 7 6种仪器记录数据的平均偏差及标准偏差 Table 7 Average deviations and standard deviations of magnitudes measured from six types of seismometers |
通过统计分析可知,不同仪器对震级偏差都有不同程度的影响,但整体偏差都不大,由表 6、表 7可见,红山台使用CTS-1型地面甚宽频带地震计,震级平均偏差小于0,标准偏差为0.30,虽然整体偏差不大,但此仪器仅红山台使用,样本单一,不具有普遍性,所以无法可靠分析CTS-1型地面甚宽频带地震计对震级偏差的影响;10个台站使用3ESPC-60三分量宽频带地震计,其震级平均偏差为-0.11—0.22,其中,5个台站偏差为负值,5个为正值,此类型地震计的整体平均偏差为0.05,接近0,标准偏差为0.16—0.21,整体浮动较小,说明此仪器对震级偏差的影响不大;6个台站使用BBVS-120地震计,其平均偏差有正有负,偏差范围-0.20—0.20,31个台站使用BBVS-60地震计,其平均偏差有正有负,偏差范围-0.28—0.32,2种仪器平均偏差趋于0,标准偏差也很小,所以这2种仪器的整体影响不大;22个台站使用FSS-3DBH地震计,其中,14个台站的平均偏差为负值,最大偏差-0.26,8个为正值,最大偏差为0.78(正定南台),但整体平均偏差趋于-0.04,标准偏差浮动较小,说明此类型地震计对震级偏差影响很小;赵县台、深州台使用BBVS-60DBH地震计,其平均偏差均为-0.13,标准偏差相同且浮动很小,标准偏差也在合理范围内。总之,仪器类型对震级偏差有一定影响,但影响较小。
4 结论及讨论依据上述统计分析可知,台站震级的测定精度受多种因素的影响。本文从量规函数、台基、仪器等方面,采用统计分析、对比等方法对各单台震级偏差进行分析校正,得到如下结论。
(1)量规函数的校正。通过对河北测震台网各单台测定的震级进行统计分析发现,震中距小于80 km时,震级偏差均为负值,说明此震中距范围内原量规函数明显偏小;震中距80—300 km时,量规函数相对趋于稳定;震中距大于300 km时,平均偏差有正有负,说明此震中距范围内原量规函数不够稳定。因此,对震中距为0—80 km、300—460 km的进行量规函数校正,拟合得到更适合河北地区的区域量规函数。
(2)台基校正。对量规函数校正前后71个单台数据进行对比发现,只有8个台站量规函数校正后平均偏差仍较大,其中,岗南台、沽源台、怀安台、临城台、孟村台正向偏大,昌黎台、临漳台、无极台负向偏大,另外,蠡县台、鹿泉台、秋树坪台、雄县台、元氏台、枣强台、正定南台、逐鹿台、遵化台等9个台站量规函数校正前后无差别,对这些台站进行校正后,震级偏差绝对值|ΔMLnm|≤0.2的占比升至63.12%,整体偏差正态分布也更收敛。
(3)仪器类型的影响。71个台站按所使用地震计的不同划分为6类,数据分类汇总后,得到最大偏差绝对值为0.13,标准偏差波动很小,整体稳定性较高,因此,仪器类型的影响不大,不需要进行校正。
综上所述,河北测震台网单台测定震级大多数是有偏差的,且偏差主要受量规函数、台基岩性等影响。本文在进行量规函数、台基校正后,大部分单台测定震级与台网平均震级间的偏差明显降低,整体震级偏差绝对值|ΔMLnm|≤0.2的占比也有所提升,这对提高河北测震台网震级测定结果的准确度有一定的意义。
陈继锋, 尹欣欣, 董宗明, 等. 2013. 甘肃地区近震震级的量规函数研究[J]. 中国地震, 29(3): 327-334. |
陈培善, 秦嘉政. 1983. 量规函数、台站方位、台基及不同测量方法对近震震级ML的影响[J]. 地震学报, 5(1): 87-98. |
李雪英, 陈立强, 赵英萍, 等. 2004. 首都圈数字遥测地震台网单台震级偏差研究[J]. 华北地震科学, 22(3): 33-39. |
吕作勇, 马晓静, 房立华. 2015. 广东地区近震ML震级的量规函数[J]. 国际地震动态, (9): 19. |
万玉杰, 赵燕杰, 马建新. 2014. 青海数字测震台网速报震级与量规函数的初步研究[J]. 高原地震, 26(4): 28-32. |
王鑫, 张帆, 尹战军, 等. 2015. 内蒙古数字测震台网单台近震震级偏差研究[J]. 地震地磁观测与研究, 36(6): 26-32. |
项月文, 陈浩, 肖孟仁, 等. 2018. 江西地区地方性震级的量规函数与台基校正值研究[J]. 中国地震, 34(1): 122-132. |
许德相, 陈文康. 2015. 自贡市加强防震减灾信息化能力建设[J]. 中国应急救援, (6): 57-59. |
詹小艳, 王俊, 缪发军, 等. 2010. 江苏数字地震台网台站震级偏差的分析[J]. 地震地磁观测与研究, 31(2): 44-49. |
张从珍, 高景春, 刁桂苓, 等. 2004. 张家口地震台和兴隆地震台地脉动信号初步分析[J]. 华北地震科学, 22(3): 56-60. |
赵明淳, 毛国良, 张从珍, 等. 2005. 河北遥测台网速报震级偏差与量规函数关系的研究[J]. 地震地磁观测与研究, 26(5): 87-94. |
 2020, Vol. 41
2020, Vol. 41

