2. 中国哈尔滨 150090 黑龙江省地震局
2. Heilongjiang Earthquake Agency, Harbin 150090, China
地震动的振幅、频谱和持时三要素决定着各类建、构筑物的地震安全性。在地震工程学中,地震动的持时和非平稳特性备受关注。地震动非平稳特性主要包括幅值非平稳特性和频率非平稳特性。幅值非平稳特性即是我们常说的强度非平稳特性,它可以表征地震动从初始振动的微弱状态持续到地震动强度较高的状态,最后衰减转弱的整体变化过程。强度包络函数能够较好地反映地震动的非平稳特性,在人工合成地震动和地震动的随机模型化等研究中,利用强度包络函数可模拟地震动的非平稳特性(霍俊荣,1989;张美玲等,2015)。因此,本文拟通过求得中国东北及邻区竖直向包络函数的参数及衰减关系来反映该区域地震动强度的非平稳特性。霍俊荣等(1991)研究了包络函数与震级、震中距和场地条件的关系及其变化特征;曹国安等(1998)为研究包络函数的特性,将对包络函数模型的研究转化为对地震记录标准差的研究;屈铁军等(1994)对SMART-1台阵局部场地强度包络函数特性进行研究,得到了参数的初步预测公式;靳超宇等(2014)对地震活动不同强度地区的包络函数进行对比分析得到了衰减规律;张美玲等(2015)对中国大陆地区231条强震记录进行包络函数相关参数研究,并与霍俊荣(1989)和肖亮(2011)的研究结果进行对比分析,得到适用于中国大陆地区地震动强度包络函数的衰减关系;俞言祥(2016)总结了近年来在近场强地震动衰减关系方面取得的重要进展。
目前,我国地震动参数衰减关系是在考虑我国强震动数据的实际情况和工程实践特征前提下建立的,主要分为青藏区、新疆区、中强地震区、东部强震区等4个部分(表 1)。根据地域特征,本文尝试建立东北及邻区的地震动衰减关系。
| 表 1 我国地震动衰减关系分区 Table 1 The subareas of seismic attenuation relationship in China |
本文使用的强震动数据来自黑龙江省地震局、吉林省地震局、辽宁省地震局和内蒙古自治区地震局数字强震动观测台网,均属于触发式强震动记录,且绝大部分为土层场地的强震动记录。由于地质构造特征使得数据量有限,故本文将不单独考虑基岩场地的数据特征。共选取了27次地震竖直方向105条记录进行研究,对所选数据采用二阶巴特沃斯因果滤波器进行带通数字滤波处理,频带范围调整为0.1—20.0 Hz。强震动数据的震中距与震级分布见图 1。

|
图 1 强震动数据的震中距与震级的分布 Fig.1 The magnitude distribution along epicentral distances for strong motion data used in the study |
目前,工程中所用的人工合成地震动主要是通过包络函数来模拟地震波的强度非平稳特性的,这在人工合成地震动过程中起到了较重要的作用(王恒知等,2009)。
2.1 强度包络函数及其模型(1)强度包络函数。地震动时程是一个随机过程,并且存在着非平稳的特性。在人工合成地震动时,通常运用1个确定性函数乘以1个平稳的随机过程来表达地震动时程的非平稳特性,即
| $ a(t) = f(t)·x(t) $ | (1) |
一般地,将此处确定性函数近似看成强度包络函数(李山有等,2003)。
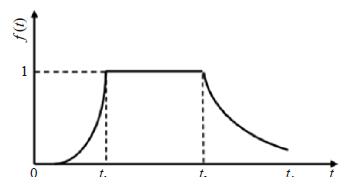
(2)强度包络函数模型。在以往研究中,利用地震动强度包络函数模型已取得较多研究结果,其中,工程上应用最广泛的是三段式包络函数模型,即由弱到强的上升阶段、相对平稳的强震动持续阶段和由强减弱的下降阶段(Housner et al,1964;Amin et al,1968;Trifunac et al,1975),其表达式为
| $ f(t) = \left\{ {\begin{array}{*{20}{l}} {(t/{t_1})^2}&{0 < t \le {t_1}}\\ 1&{{t_1} < t \le {t_2}}\\ {{{\rm{e}}^{ - c(t - {t_2})}}}&{{t_2} < t \le {t_{\rm{d}}}} \end{array}} \right. $ | (2) |
式中,t1、t2分别为强震平稳段的起、止时刻;此外,我们用来表示平稳段的持续时间,即ts = t2 - t1,它能较好地反映t2的特性;c为地震动的衰减因子;td为地震动的总持续时间,简称“总持时”。图 2为三段式包络函数示意图。
|
图 2 强度包络函数三段式模型示意 Fig.2 Schematic map of a time history envelope function and its parameters |
(1)t1和ts。t1值表示上升段参数,这里考虑为自相对地面振动开始明显区别于白噪声时至达到平稳振动段之间的时间差。上升段左端用表示,即地震动时程的振动幅值或能量开始明显超过白噪声的时刻,其确定方式采用绝对幅值的方法,即将0.5 s时间窗内峰值包线值大于1 Gal时的值确定为值(肖亮,2011)。
地震动记录的能量主要集中在平稳段,这部分能量对结构振动有明显的作用。其中,能量持时ts被广泛应用于工程实践中,不同的能量持时对结构的破坏能力不同因70%能量持时是从能量分布函数中截取总能量的70%所持续的时间,故本文采用70%的能量持时进行研究具有一定的实践意义(袁峰等,2017)。由于本文选用了中强地震记录,因此选用5%—75%作为70%能量持时的阈值是相对合适的(Bolt,1973;Shoji et al,2005),公式如下
| $ {I_{{\rm{all}}}} = \frac{\pi }{{2{\rm{g}}}}\int_0^{{t_\rm{d}}} {{a^2}(t)} {\rm{d}}t $ | (3) |
| $ {I_{\rm{5}}} = \frac{\pi }{{2{\rm{g}}}}\int_0^{{t_1}} {{a^2}(t)} {\rm{d}}t $ | (4) |
| $ {I_{{\rm{75}}}} = \frac{\pi }{{2{\rm{g}}}}\int_0^{{t_2}} {{a^2}(t)} {\rm{d}}t $ | (5) |
| $ {I_{\rm{5}}}/{I_{{\rm{all}}}} = 5\%, {I_{{\rm{75}}}}/{I_{{\rm{all}}}} = 75\% $ | (6) |
其中,Iall为地震动记录的总能量;I5、I75分别为地震动记录总能量的5%、75%。因此,根据式(4)、(5)便可求得t1、t2。ts由(t2 - t1)获得。
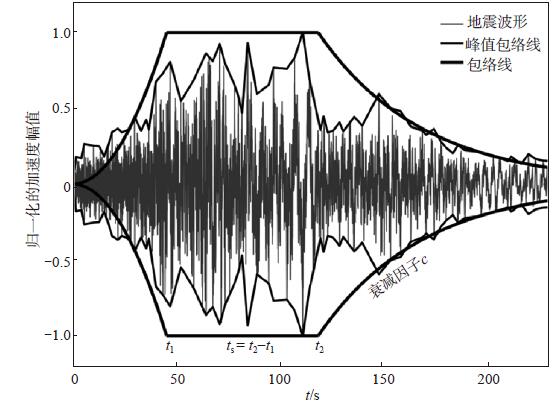
(2)衰减因子c。衰减因子c控制着地震动下降过程的衰减速率,本文采用多峰值搜索法(张美玲,2014;张美玲等,2015)对包络函数衰减段f (t) =e-c(t-t2)应用最小二乘法拟合,从而得到c值。图 3为真实记录下使用多峰值搜索法获得的时程强度包络函数及参数。
|
图 3 实际记录中多峰值搜索法获得的包络线(据张美玲等,2015) Fig.3 The envelope obtained with a multi-peak search method for real records (Zhang Meiling,2015) |
地震动时程幅值包络线的特征与震级、震中距、场地条件及其他因素有关,其中,与震级、震中距之间的相关性更强,所以,通常用下面的公式来表示衰减关系(俞言祥,2002;肖亮,2011;肖亮等,2012)
| $ \lg Y = {k_1} + {k_2}M + {k_3}\lg (R + {R_0}) + \varepsilon $ | (7) |
式中,Y为强度包络函数的模型参数(t1、ts、c);k1、k2、k3为回归系数;M为震级;R为震中距;R0为与震级相关的近场距离饱和因子;ε为回归残差的正态随机变量。
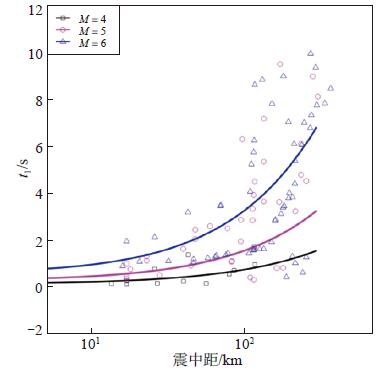
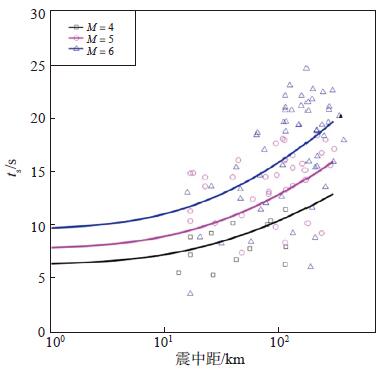
4 对比分析按照上述方法,同时在震级和震中距2个方向应用单随机变量加权最小二乘法对包络函数的参数进行统计回归(刘志平等,2008),计算结果见表 2。所得结果适用于震级为3.3—5.8级、震中距为0—371 km的土层场地地震动记录。根据上述计算结果绘制包络函数参数的拟合曲线及数据分布图,结果见图 4、图 5、图 6。
| 表 2 包络函数相关参数的回归系数及残差 Table 2 Regression coefficients and residuals of the relevant parameters of the envelope function |
|
图 4 上升段持时t1的数据分布及拟合曲线 Fig.4 Distribution of rising duration t1 along epicentral distance and fitting curves for different magnitudes |
|
图 5 平稳段持时ts的数据分布及拟合曲线 Fig.5 Distribution of stable duration ts along epicentral distance and fitting curves for different magnitudes |
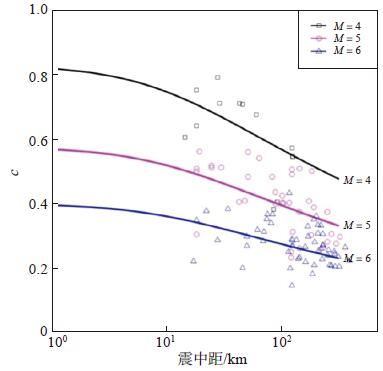
|
图 6 下降段参数c的数据分布及拟合曲线 Fig.6 Distribution of decline parameter c along epicentral distance and fitting curves for different magnitudes |
按照上述计算结果,并结合参数的数据分布情况(图 4,图 5,图 6),基于前提条件一致的原则,本文与霍俊荣(1989)的竖直向土层记录计算所得结果(霍俊荣,1989;霍俊荣等,1991)进行比较分析,将回归统计结果代入式(7)中,绘制与霍俊荣(1989)结果的对比图,结果见图 7、图 8、图 9。
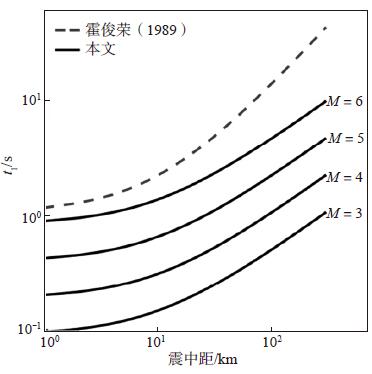
|
图 7 上升段持时t1的回归关系对比 Fig.7 Comparison of different attenuation relationships for rising duration t1 |
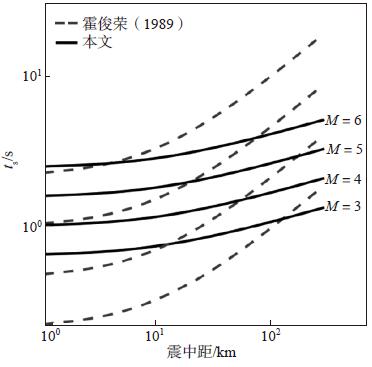
|
图 8 上升段持时平稳段持时ts的回归关系对比的回归关系对比 Fig.8 Comparisonin of different attenuation relationships for stable duration ts |
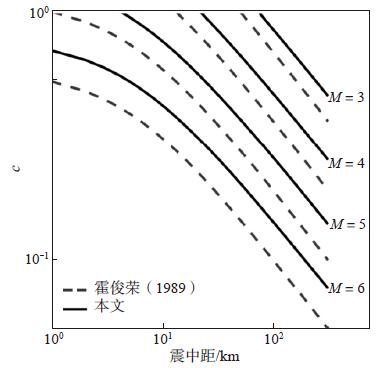
|
图 9 下降段参数c的回归关系对比 Fig.9 Comparison of different attenuation relationships for decline parameter c |
由图 7可见,上升段持时随震级的增加呈增大趋势,而霍俊荣(1989)认为t1与震级无关。但是,在工程实践中发现,上升段持时与震级有明显的正相关性。
由图 8可见,随震中距的增加本文结果比霍俊荣(1989)结果上升趋势明显缓慢,且不同震级之间的差距小于霍俊荣(1989)结果。其原因在于本文选取的强震动记录震级普遍偏小,因而记录的平稳段持续时间较短;此外,选取的震级较集中也造成了不同震级之间的结果更加接近。
由图 9可见,c值随着震中距的增加而减小,表明记录尾部在不断地衰减,并且c值越大衰减越快;c值越小衰减越慢。大震级记录中的长周期成分形成了频散效应(霍俊荣等,1991),而本文选取的震级整体较小,振动过程中释放的能量相对较少,长周期成分不丰富,所以,与霍俊荣(1989)相同震级的结果相比,本文结果显示整体衰减较快。
5 结论从本文收集到的数据来看,震级主要集中在4.5—5.0,其中,大部分为土层场地的结果,通过与霍俊荣(1989)的结果进行对比发现,基于竖直向强度包络函数3个参数的衰减关系整体符合衰减规律的分布特征。本文关于强震动包络函数参数衰减关系的计算结果,为适用于中国东北及邻区地震动时程包络函数参数的衰减关系,具体为震级3.3—5.8、震中距0—371 km的土层场地。虽然本文选用的强震动记录数量有限,但是统计回归结果尚可。今后应进一步完成东北及邻区水平向强震动记录的相关研究,以使该区域的研究更具有完整性和统一性。
本文数据主要来源于中国东北及邻区的强震动记录。在此特别感谢辽宁省地震局李永振、吉林省地震局刘冰冰和内蒙古自治区地震局王树波等3位老师提供数据及相关的指导和帮助。
曹国安, 张鸿儒. 1998. 地震动强度包络函数模型[J]. 北方交通大学学报, 22(1): 29-38. |
霍俊荣.近场强地面运动衰减规律的研究[D].哈尔滨: 中国地震局工程力学研究所, 1989.
|
霍俊荣, 胡聿贤, 冯启民. 1991. 地面运动时程强度包络函数的研究[J]. 地震工程与工程振动, 11(1): 1-12. |
靳超宇, 李伟, 陈方颖. 2014. 加速度时程包络函数地区性差异初步研究[J]. 世界地震工程, 30(4): 240-246. |
李山有, 金星, 刘启方, 等. 2003. 中国强震动观测展望[J]. 地震工程与工程振动, 23(2): 1-7. |
刘志平, 石林英. 2008. 最小二乘法原理及其MATLAB实现[J]. 中国西部科技, 7(17): 33-34. |
屈铁军, 王君杰, 王前信. 1994. 局部场地上地震动的强度包络函数的特性研究[J]. 地震工程与工程振动, 14(3): 68-80. |
王恒知, 石玉成, 卢育霞, 等. 2009. 人工拟合地震动时程参数对场地反应的影响分析[J]. 西北地震学报, 31(2): 126-130. |
肖亮.水平向基岩强地面运动参数衰减关系研究[D].北京: 中国地震局地球物理研究所, 2011.
|
肖亮, 俞言祥. 2012. 基于NGA强震数据的地震动时程强度包络函数衰减关系研究[J]. 国际地震动态, (6): 143. |
俞言祥.长周期地震动衰减关系研究[D].北京: 中国地震局地球物理研究所, 2002.
|
俞言祥, 李山有, 肖亮. 2013. 为新区划图编制所建立的地震动衰减关系[J]. 震灾防御技术, 8(1): 24-33. |
俞言祥. 2016. 新一代地震区划图地震动参数衰减关系的建立与特点分析[J]. 城市与减灾, (3): 34-38. |
袁峰, 邱卓, 钟菊芳. 2017. 能量持时阈值的选取分析[J]. 南昌航空大学学报:自然科学版, 31(2): 7-11. |
张美玲.地震动强度包络函数相关参数确定[D].哈尔滨: 中国地震局工程力学研究所, 2014.
|
张美玲, 李山有, 卢建旗, 等. 2015. 中国大陆地区地震动时程强度包络函数研究[J]. 地震工程与工程振动, 35(4): 60-70. |
Amin M, Ang A H-S. 1968. Nonstationary stochastic models of earthquake motions[J]. Journal of the Engineering Mechanics Division, 94(2): 559-584. |
Bolt B A. Duration of strong ground motion[C]//Proceedings of the 5th World Conference on Earthquake Engineering. Rome, 1973: 1 304-1 313.
|
Housner G W, Jennings P C. 1964. Generation of artificial earthquakes[J]. Journal of the Engineering Mechanics Division, 90(1): 113-152. |
Shoji Y, Tanii K, Kamiyama M. 2005. A study on the duration and amplitude characteristics of earthquake ground motions[J]. Soil Dynamicsand Earthquake Engineering, 25(7/8/9/10): 505-512. |
Trifunac M D, Brady A G. 1975. A study on the duration of strong earthquake ground motion[J]. Bull Seismol Soc Am, 65(3): 581-626. |
 2020, Vol. 41
2020, Vol. 41

