陆远忠等(1982, 1983)研究了在一些大地震发生前存在孕震空区。此后,空区研究受到重视并较快发展,研究中还提出了背景空区和孕震空区等概念,空区成为地震活动图像分析的重要方法和地震预测预报的重要指标。实际上,空区方法是研究地震活动空间分布特征的一种定性方法,在大地震孕育阶段由较大震级地震围成的背景空区可能具有相对普遍的意义。梅世蓉等(1993, 1997)在总结我国华北地区60次历史地震震例的基础上提出地震空白区的概念,指出6级以上大地震前若干年出现不同强度的地震环绕大震震中分布的特殊状态,并形成地震包围的“空白区”,空白区内地震活动性很低,空白区外活动性较高。国内外关于地震空区的研究从未停止,产出了较丰富的研究成果,如闻学泽等(2008)、曲延军等(2010)、梁春涛等(2018)、张博等(2018)、Rajendran等(2005)、Kulinich等(2007)、Ozawa等(2016)以及Yang等(2017)的工作,均从不同角度研究了地震空区问题。
但是,短期内由小震级地震围成的孕震空区往往存在较大随意性,如震级选取、空区内地震的取舍等都存在很大不确定性。因此,不同研究者所圈出的空区可能并不相同,这给分析工作带来一定困难。杨建思(1988)在计算机自动识别地震空区的方法、程序及应用方面开展了工作。由定性研究走向定量研究,是空区研究的必由之路,本文尝试应用随机场方法,通过震例来定量研究地震活动“围空”分布问题。
1 地震活动场分析方法 1.1 地震活动场地震活动场研究可简略地描述为引用随机场概念,通过自然正交展开方法研究特定地区及特定地震的地震活动场问题。根据随机函数论原理,将地震活动要素变量看作空间和时间的函数,提出地震活动场的基本概念。通过区域网格化方法构建空间和时间相关的地震活动场函数矩阵,经过自然正交函数展开,挑选出占总场主要成分的典型场,从而在目前的认识水平上,通过只引入少数几个主要典型场和主要典型场的时间因子即可对地震活动这种复杂的自然过程进行定量数学描述,并对其时空特征进行研究。该方法将地震活动表示为n个相互独立的正交分量的叠加(即分解为n个相互独立的典型场),每个典型场代表地震活动空间分布的一种模式(或类型),典型场及其时间因子共同描述地震活动的一种状态(杨明芝等,2016)。
在杨明芝等(2004)引用随机场概念,通过自然正交展开方法研究了宁夏及邻区地震活动能量场问题后,又采用该方法研究了2008年汶川8.0级地震前震中周围区域能量场(杨明芝等,2012)。并在此基础上,通过大量震例研究了大地震前区域活动场的时间因子异常特征,取得了有意义的结果(杨明芝等,2013)。其他代表性的相关工作有马禾青等(2012)、罗国富等(2014, 2016, 2018)、杨明芝等(2017)和Ma等(2018)。以上研究表明,应用自然正交展开方法将地震活动要素变量作为随机场在探索地震活动异常方面是有效的,同时也表明,随机场方法适用于描述和研究地震活动性。有关地震活动场研究的具体方法,相关文献均有详细论述,不再赘述。
在各种变量中,表征地震活动物理状态和物理性质的2个最重要变量是地震能量和地震频次。当地震活动要素变量取能量时研究对象为能量场(杨明芝等,2013),取频次时则为频次场(马禾青等,2020),还可以研究应变场(杨明芝等,2017)、地震综合变量场(马禾青等,2017)等。区域网格划分时可以以研究对象为中心选取研究区域,采取矩形网格划分的方法。另一方面,在大地震的孕育和发生过程中,沿断裂带地震释放的能量和空间分布也会发生改变,因此,可以沿构造断裂带选取若干能量观测网格,应用自然正交函数展开方法,分析断裂带上网格区域的地震能量动态变化,寻找可能的地震地球物理信息(杨明芝等,2011)。事实上,地震在孕育过程中震源周围不同距离的地震活动性也可能会发生不同程度的变化,地震活动的某一随机变量会随与孕震中心距离的不同出现不同反映。为此,可以把地震活动场函数F看作距离r的函数,研究活动场随距离的变化情况,环形带表示的地震活动场即称为环形场(马禾青等,2018)。
1.2 环形带地震活动场选择以震中为中心,以半径rn = n×dr向外扩展,形成半径dr的1个中心圆形区和n-1个环带形区域。每个环带的面积为π×(2n-1)×dr2,对这n个小环形区各时段的随机变量进行统计计算,并取单位面积平均值Fij,表示为如下矩阵形式
| $ F = \left[ {\begin{array}{*{20}{c}} {{F_{11}}}&{{F_{12}}}& \ldots &{{F_{1n}}}\\ {{F_{21}}}&{{F_{22}}}& \ldots &{{F_{2n}}}\\ \vdots & \vdots & \ldots & \vdots \\ {{F_{m1}}}&{{F_{m2}}}& \ldots &{{F_{mn}}} \end{array}} \right] $ | (1) |
其中,Fij(i = 1, 2, …, m;j = 1, 2, …, n)为第j个环形带第i个时段单位面积随机变量的观测值或距平值。式(1)表示随机变量与距离r之间的函数关系,如果取随机变量为地震释放能量或频次,式(1)就表示以时间t和空间距离r为自变量的能量场或频次场函数。对式(1)进行自然正交函数展开,求解得到n个特征值和相应的特征向量,并计算时间权重系数(时间因子),由此分析场的时空分布特征及异常变化(马禾青等,2018)。
基于环形带区域形状的特质,尝试研究地震空区问题。选择1979年7月9日江苏溧阳6.0级和1979年3月15日云南普洱6.8级地震空区,应用环形带地震活动场方法研究2次地震和地震空区。这2次地震空区较有代表性,前者是一个非常理想的空区,空区内没有小地震活动,后者空区内仍有小地震活动。
2 1979年7月9日江苏溧阳6.0级地震空区以1979年7月9日江苏溧阳6.0级地震为例,通过随机场方法分析在存在地震空区的情况下能量场和频次场的影响及特征。
2.1 环形带地震活动场分析结果取1970年1月至1979年6月为研究时段,取时间间隔为3个月,对资料进行时间离散化处理。以地震震中为中心划分环形区带,并进行能量和频次统计(能量单位取1010J),取距平值,得到一个m×n阶的距平活动场矩阵函数。然后对其进行自然正交函数展开计算,求解协方差矩阵R = F'F的n个特征值和相应的特征向量以及典型场的时间因子序列。表 1给出了此次地震的环形带划分参数、主要典型场的特征值、贡献率及异常基本情况。图 1为此次地震的环形带活动场随时间的变化。
| 表 1 1979年江苏溧阳6.0级地震环形区能量场主要典型场的特征值、贡献率及异常 Table 1 The eigenvalue, contribution rate, and anomaly of main typical field of the ring belt energy field before the Liyang M 6.0 earthquake in Jiangsu, 1979 |
|
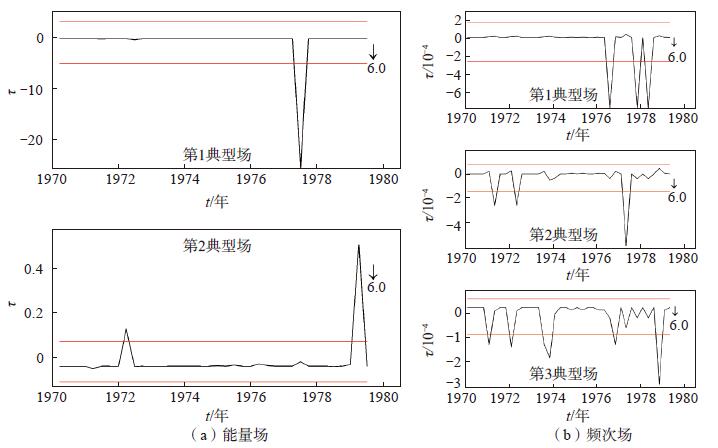
图 1 1979年7月9日江苏溧阳6.0级地震前环形区域活动场典型场随时间的变化 红线表示均方差,震前3 年内超出红线的被看作异常 Fig.1 The time factor curves of the typical field of the ring belt activity field before the Liyang M 6.0 earthquake in Jiangsu occurred on July 9, 1979 |
由表 1、图 1可见,由于此次地震的环形带能量场和频次场的前2、3个典型场的拟合精度均大于0.950 0,因此,分别取前2、3个典型场就足以代表原始场。能量场异常形态十分清晰,第1、2典型场时间因子异常分别出现在震前2年及3个月,空间上主要出现在距震中21—40 km、81—100 km范围的环形带区域内。同时,震中周围的几个环形区内地震频次场亦出现异常显示。
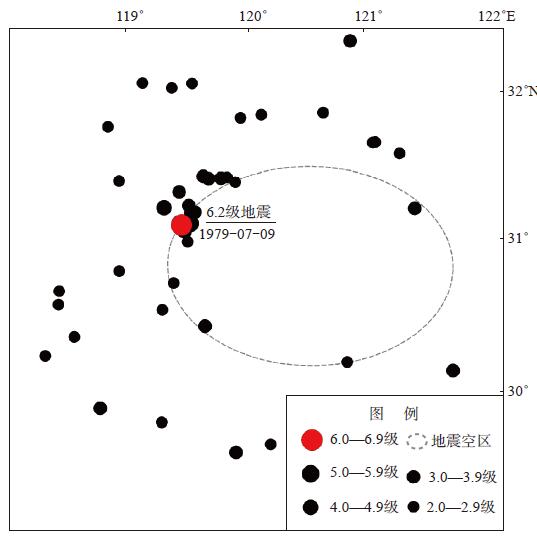
2.2 空区环形带地震活动场分析结果1979年7月9日江苏溧阳6.0级地震前已积累近10年的观测资料,ML≥2.5地震记录未遗漏。图 2为利用ML≥2.5地震所做的1974年1月至震前区域地震震中分布和地震空区。
|
图 2 1979年7月9日江苏溧阳6.0级地震前震中分布及地震空区 Fig.2 The seismic distribution and seismic gap before the Liyang M 6.0 earthquake in Jiangsu on July 9, 1979 |
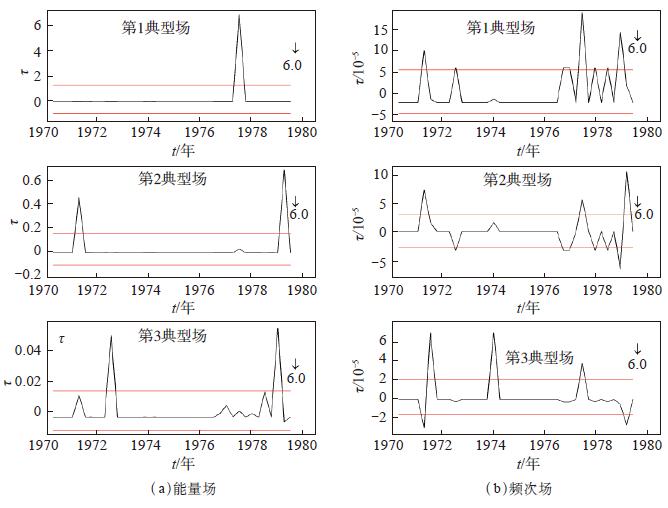
分析地震空区的地震活动场,仍采用环形区域网格。选取空区的中心(31.0°N,120.0°E)为圆心,取dr = 20 km,n = 6,计算距平能量矩阵和距平频次场矩阵,计算时段取1970年1月至1979年6月,取样时间间隔为3个月。表 2为自然正交函数展开得到的能量场和频次场前3个典型场的特征值和贡献率;图 3为能量场和频次场的时间因子曲线;表 3为各典型场时间因子异常情况。由图 1、3可见,2种情况下曲线的异常表现形态存在异同性。
| 表 2 1979年江苏溧阳6.0级地震前能量场和频次场的特征值和贡献率 Table 2 The eigenvalues and contribution rates of the energy field and frequency field before the Liyang M 6.0 earthquake in Jiangsu, 1979 |
|
图 3 1979年江苏溧阳6.0级地震前能量场和频次场随时间的变化 红线表示均方差,震前3年内超出红线的被看作异常 Fig.3 The time factor of the energy field and frequency field before the Liyang M 6.0 earthquake in Jiangsu, 1979 |
| 表 3 1979年江苏溧阳6.0级地震前能量场和频次场异常情况汇总 Table 3 Summary of the energy field and frequency field anomalies before the Liyang M 6.0 earthquake in Jiangsu, 1979 |
表 4给出了江苏溧阳6.0级地震的能量场和频次场前3个典型场的分量值。由表 4可见,第1、2、3个环形带区所对应的典型场的分量值都等于0,说明在研究时段空区中心周围约3 km×20 km的范围内没有发生ML≥2.5地震,至少近10年的时间内该半径为60 km的区域为地震空白区。综上所述得到:①1979年江苏溧阳6.0级地震前地震活动的空区图像具有地球物理意义,其能量场和频次场表现出明显异常变化;②空区中心周围的几个环形带对典型场的贡献为0,能量场和频次场时间因子异常影响主要集中在第4、5、6这3个环带;③根据对异常出现时间和空间分布的分析可知,1979年3月7日发生在空区边界附近的ML 3.9地震是“逼近地震”。
| 表 4 1979年江苏溧阳6.0级地震前能量场和频次场前3个典型场的分量值 Table 4 The component values of the first three typical fields of the energy field and frequency field before the Liyang M 6.0 earthquake in Jiangsu, 1979 |
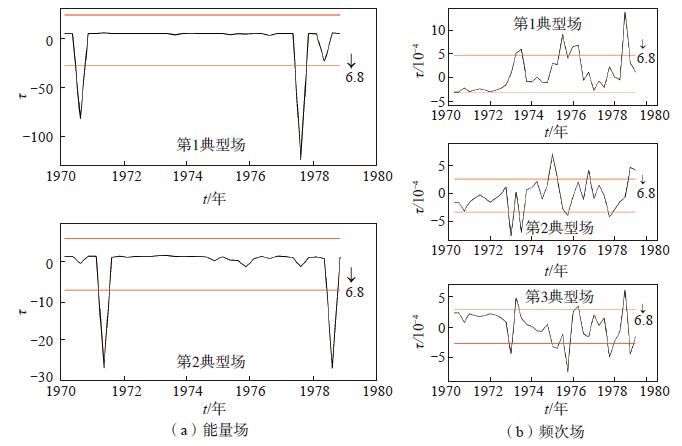
取1970年1月至1978年12月为研究时段,表 5给出了1979年3月15日云南普洱6.8级地震的环形带划分参数、主要典型场的特征值、贡献率及异常基本情况;图 4为此次地震的环形带活动场随时间的变化。由于此次地震的环形带能量场前2个典型场的拟合精度已大于0.99,而频次场前3个典型场的拟合精度已达0.90,因此分别取前2、3个典型场代表原始场。由图 4可见,能量场异常形态较清晰,第1和第2典型场及其时间因子异常分别出现在震前1.5年及6个月,空间上主要表现在距震中37—54 km以及55—72 km范围的环形带区域内。同时,震中周围的几个环形区内地震频次出现异常显示。
| 表 5 1979年云南普洱6.8级地震环形区能量场主要典型场的特征值、贡献率及异常 Table 5 The eigenvalue, contribution rate, and anomaly of the main typical field of the ring belt energy field before the Puer M 6.8 earthquake in Yunnan, 1979 |
|
图 4 1979年3月15日云南普洱6.8级地震前环形区域活动场典型场随时间的变化 红线表示均方差,震前3年内超出红线的被看作异常 Fig.4 The time factor curves of the typical field of the ring belt activity field before the Puer M 6.8 earthquake in Yunnan occurred on Mar. 15, 1979 |
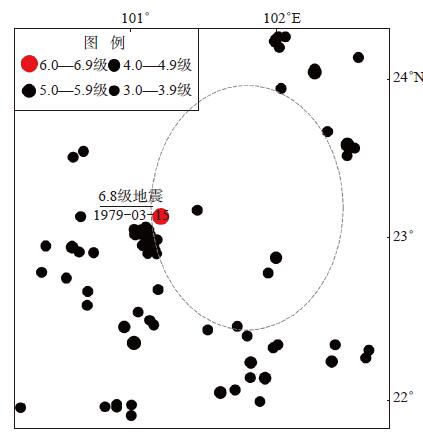
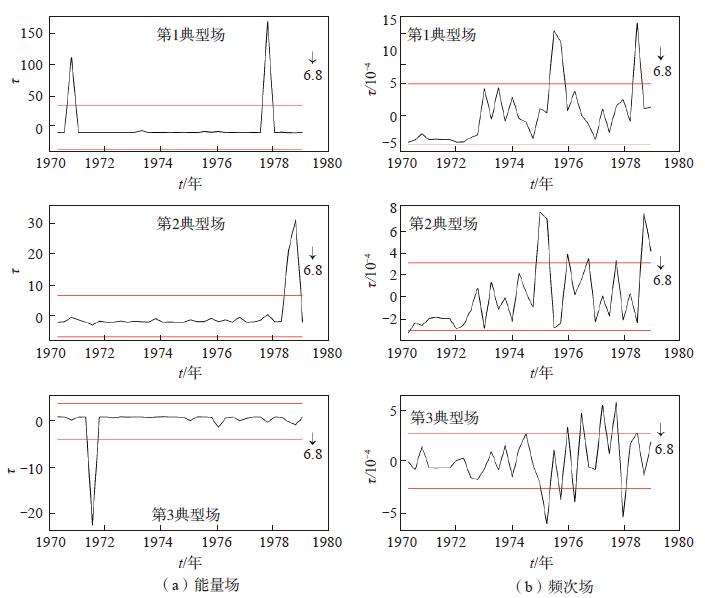
图 5为1976年6月至震前ML≥3.2地震围成的空区,空区中心约在(23.3°N,101.6°E)。以此为圆心,能量场取dr = 20 km,n = 5,频次场取dr = 22 km,n = 5,计算距平能量场矩阵和距平频次场矩阵,然后进行自然正交函数展开。表 6为自然正交函数展开得到的能量场和频次场前3个典型场的特征值及贡献率;图 6为能量场和频次场的时间因子曲线;表 7为此次地震前能量场和频次场前3个典型场时间因子异常统计。2种场的时间因子曲线在震前都表现出异常变化,说明空区具备异常活动图像特征。由图 4和图 6可见,2种情况下曲线的异常表现形态存在异同性。
|
图 5 1979年云南普洱6.8级地震前震中分布及地震空区 虚线内为地震空区 Fig.5 The seismic distribution and seismic gap before the Puer M 6.8 earthquake in Yunnan, 1979 |
| 表 6 1979年云南普洱6.8级地震前能量场和频次场的特征值和贡献率 Table 6 The eigenvalues and contribution rates of the energy field and frequency field before the Puer M 6.8 earthquake in Yunnan, 1979 |
|
图 6 1979年3月15日云南普洱6.8级地震前能量场和频次场随时间的变化 红线表示均方差,震前3年内超出红线的被看作异常 Fig.6 The time factor of the energy field and frequency field before the Puer M 6.8 earthquake in Yunnan, 1979 |
| 表 7 1979年云南普洱6.8级地震前能量场和频次场异常情况汇总 Table 7 Summary of the energy field and frequency field anomalies before the Puer M 6.8 earthquake in Yunnan, 1979 |
表 8为普洱6.8级地震的能量场和频次场前3个典型场的分量值。与前例不同,该地震空区内ML≤3.2地震仍然有活动,空区内环带对应的典型场分量值并不为0。其中,由于能量场是大震级地震起主导作用,故第1环形区的分量值很小,而第2、3、4环形区对应的分量值较大,在场中起主要作用。频次场则由于空区内仍有小震级地震活动,故围空区中心几个环形带对应分量值比重仍然较大,看不出分量值减小的特征。
| 表 8 1979年云南普洱6.8级地震前能量场和频次场前3个典型场的分量值 Table 8 The component values of the first three typical fields of the energy field and frequency field before the Puer M 6.8 earthquake in Yunnan, 1979 |
综上所述,当区域内地震活动出现空区图像时,利用环形带能量场或频次场自然正交函数展开方法研究空区及周围地震活动的变化情况,可能是判断地震危险区和进行地震活动趋势分析的方法。
本文讨论的2个震例较为典型,毋庸置疑,本文工作给如何开展地震空区的定量研究带来了一定启发,但是仍然需要更丰富的震例和更加深入的工作加以验证。
其实,地震活动的空间分布复杂,定性方法提出的“空区”并没有严格的定义。从地震活动场的角度分析,真正定量意义上的空区,应该是场的典型场在空区内的分量值很小,如1979年7月9日江苏溧阳6.0级地震,其围空区内部分量值为0,但这种定量意义上的空区并不多见。如果超出空区范围能够看到出现异常,那么正在跟踪的空区很可能为孕震空区,需警惕空区周围未来地震的发生。
梁春涛, 黄焱羚, 王朝亮, 等. 2018. 汶川和芦山地震之间地震空区综合研究进展[J]. 地球物理学报, 61(5): 1996-2010. |
陆远忠, 沈建文, 宋俊高. 1982. 地震空区与"逼近地震"[J]. 地震学报, 4(4): 327-336. |
陆远忠, 王炜, 沈建文. 1983. 地震空区与逼近地震(续)[J]. 地震学报, 5(2): 129-144. |
罗国富, 曾宪伟, 马禾青, 等. 2014. 岷县漳县6.6级地震前地震活动能量场分析[J]. 地震工程学报, 36(2): 314-319. |
罗国富, 屠泓为, 曾宪伟, 等. 2016. 2014年云南景谷6.6级地震前后活动能量场分析[J]. 地震, 36(3): 125-134. |
罗国富, 刘忠旺, 丁凤和, 等. 2018. 2017年四川九寨沟7.0级地震前地震应变场分析[J]. 地震工程学报, 40(6): 1322-1330. |
马禾青, 杨明芝. 2012. 2010年青海玉树7.1级地震能量场研究[J]. 地震研究, 35(4): 485-490. |
马禾青, 杨明芝. 2017. 地震活动多参数综合变量的异常分析方法——以青海两次7级地震为例[J]. 地震, 37(4): 50-57. |
马禾青, 杨明芝. 2018. 环形带地震活动能量场分析方法[J]. 中国地震, 34(4): 809-817. |
马禾青, 杨明芝, 罗国富. 2020. 地震活动频次场研究[J]. 地震, 40(3): 99-111. |
梅世蓉, 冯德益, 张国民, 等. 1993. 中国地震预报概论[M]. 北京: 地震出版社.
|
梅世蓉, 李宣瑚.华北地区强震前地震活动长期演变过程的共性[M]//国家地震局预测预防司, 地震短临预报的理论与方法——"八五"公关三级课题论文集.北京: 地震出版社, 1997.
|
曲延军, 王海涛, 邬成栋, 等. 2010. 中国大陆地震空区统计特征分析[J]. 地震学报, 32(5): 544-556. |
闻学泽, 范军, 易桂喜, 等. 2008. 川西安宁河断裂上的地震空区[J]. 中国科学:地球科学, 38(7): 797-807. |
杨建思. 1988. 计算机自动识别地震空区的方法、程序及应用[J]. 地震地磁观测与研究, 9(2): 63-76. |
杨明芝, 赵卫明. 2004. 宁夏及邻近地区地震活动能量场的统计分析[J]. 地震学报, 26(5): 516-522. |
杨明芝, 马禾青. 2011. 汶川8.0级地震前龙门山断裂带能量场变化[J]. 中国地震, 27(3): 260-267. |
杨明芝, 马禾青. 2012. 汶川8.0级地震区域地震能量场分析[J]. 地球物理学进展, 27(3): 872-877. |
杨明芝, 马禾青. 2013. 大地震前区域能量场的时间因子异常特征[J]. 地震, 33(3): 107-115. |
杨明芝, 马禾青. 2016. 地震活动场理论及异常分析方法[M]. 北京: 地震出版社.
|
杨明芝, 马禾青, 罗国富, 等. 2017. 中国大陆6级以上强震前的地震应变场研究[J]. 地球物理学报, 60(10): 3804-3814. |
张博, 张辉, 冯建刚, 等. 2018. 2017年九寨沟7.0级地震前不同级别地震空区的演化过程分析[J]. 中国地震, 34(4): 765-771. |
Kulinich R G, Karp B Y, Baranov B V, et al. 2007. Structural and geological characteristics of a "seismic gap" in the central part of the Kuril Island Arc[J]. Russian Journal of Pacific Geology, 1(1): 3-14. DOI:10.1134/S1819714007010022 |
Ma H Q, Yang M Z. 2018. Discussions on several problems about the seismic activity field[J]. Acta Geologiaca Sinica, 92(Z2): 93-95. |
Ozawa S, Tobita M, Yarai H. 2016. A possible restart of an interplate slow slip adjacent to the Tokai seismic gap in Japan[J]. Earth, Planets and Space, 68(1): 54. DOI:10.1186/s40623-016-0430-4 |
Rajendran C P, Rajendran K. 2005. The status of central seismic gap: a perspective based on the spatial and temporal aspects of the large Himalayan earthquakes[J]. Tectonophysics, 395(1/2): 19-39. |
Yang Y H, Liang C T, Li Z Q, et al. 2017. Stress distribution near the seismic gap between Wenchuan and Lushan earthquakes[J]. Pure and Applied Geophysics, 174(6): 2257-2267. DOI:10.1007/s00024-016-1360-6 |
 2020, Vol. 41
2020, Vol. 41

