2. 中国上海 201602 上海佘山地球物理国家野外科学观测研究站
2. Shanghai Sheshan National Geophysical Observatory and Research Station, Shanghai 201602, China
YRY-4型四分量钻孔应变仪观测数据基本符合自洽方程,当数据不符合自洽方程时,一个可能原因是,井下探头中元件的灵敏度发生了变化。邱泽华等(2005)、易志刚等(2007)、阚宝祥等(2007)、吴立辛等(2010)、柳忠旺等(2014)均在研究中提及,可利用四分量钻孔应变仪互相垂直方向应力之和为不变量的特点,依次以每个元件为标准,分别计算各元件灵敏度。
佘山地震基准台(下文简称佘山台)于2006年3月安装YRY-4分量式钻孔应变仪,运行至今,井下探头中的元件出现不同程度的老化。为保障钻孔应变观测资料的准确性和科学性,有必要在数据分析前进行实地相对标定。本文根据钻孔应变仪工作原理,参照邱泽华(2017)提出的实地相对标定思路和方法,对2013—2018年佘山台钻孔应变观测资料进行矫正计算,利用C95信度值,来评价矫正前后的观测资料质量。具体方法如下:①变化矫正,利用观测资料原始值进行实地相对标定计算,得到4个元件的灵敏度系数K,并对各元件进行矫正,最后对矫正后的数据进行质量评估;②差分矫正,对观测资料原始值进行差分计算,然后进行实地相对标定计算,得到各元件灵敏度系数K,对各元件进行矫正,并对矫正后的数据进行质量评估。
1 基本公式分量钻孔应变仪一般直接测量孔径相对变化。根据“钻孔加衬模型”,当远处有均匀水平主应力ε1和ε2时,钻孔沿θ方向的理论孔径相对变化为
| $ {S_\theta } = A({\varepsilon _1} + {\varepsilon _2}) + B({\varepsilon _1} - {\varepsilon _2}){\rm{cos}}{\kern 1pt} {\kern 1pt} 2(\theta - \varphi ) $ | (1) |
式中,φ为ε1的方位角,而A和B是耦合系数,与套筒内径和外径、围岩等效杨氏模量、泊松比、套筒材料杨氏模量和泊松比有比较复杂的关系。
实地相对标定原理如下:用Ri代表元件i的观测读数,Ki代表元件i的灵敏度,则元件i的孔径相对变化测值Si为
| $ {S_i} = {K_i}{\kern 1pt} {R_i} $ | (2) |
可知,对于各向同性弹性介质,确定平面应变状态,只需观测该平面内3个方向的孔径相对变化(3个方向的孔径相对变化测值是相互独立的)。对于四分量探头,有4个方向的测值可供使用,可构成4种包含3个方向的孔径相对变化测值的组合。这4个方向的测值不是相互独立的,它们之间的关系可用简单公式给出,设S1、S2、S3、S4为各元件的实际观测值,则
| $ \left\{ \begin{array}{*{35}{l}} {{S}_{1}}={{S}_{{{\theta }_{1}}}}=A({{\varepsilon }_{1}}+{{\varepsilon }_{2}})+B({{\varepsilon }_{1}}-{{\varepsilon }_{2}})\text{cos}2({{\theta }_{1}}-\varphi ) \\ {{S}_{2}}={{S}_{{{\theta }_{1}}+{}^{\pi }\!\!\diagup\!\!{}_{4}\;}}=A({{\varepsilon }_{1}}+{{\varepsilon }_{2}})-B({{\varepsilon }_{1}}-{{\varepsilon }_{2}})\text{sin}2({{\theta }_{1}}-\varphi ) \\ {{S}_{3}}={{S}_{{{\theta }_{1}}+{}^{\pi }\!\!\diagup\!\!{}_{2}\;}}=A({{\varepsilon }_{1}}+{{\varepsilon }_{2}})-B({{\varepsilon }_{1}}-{{\varepsilon }_{2}})\text{cos}2({{\theta }_{1}}-\varphi ) \\ {{S}_{4}}={{S}_{{{\theta }_{1}}+{}^{3\pi }\!\!\diagup\!\!{}_{4}\;}}=A({{\varepsilon }_{1}}+{{\varepsilon }_{2}})+B({{\varepsilon }_{1}}-{{\varepsilon }_{2}})\text{sin}2({{\theta }_{1}}-\varphi ) \\ \end{array} \right. $ | (3) |
将式中2个互相垂直方向的孔径相对变化的测值分别相加,得自检方程,公式如下
| $ {{S_1} + {S_3} = {S_2} + {S_4}} $ | (4) |
将式(2)代入式(4),得
| $ {{K_1}{R_1} - {K_2}{R_2} + {K_3}{R_3} - {K_4}{R_4} = 0} $ | (5) |
将式(5)两边同除以Ki,得
| $ {{K_{11}}{R_1} - {K_{21}}{R_2} + {K_{31}}{R_3} - {K_{41}}{R_4} = 0} $ | (6) |
| $ {{K_{12}}{R_1} - {K_{22}}{R_2} + {K_{32}}{R_3} - {K_{42}}{R_4} = 0} $ | (7) |
| $ {{K_{13}}{R_1} - {K_{23}}{R_2} + {K_{33}}{R_3} - {K_{43}}{R_4} = 0} $ | (8) |
| $ {{K_{14}}{R_1} - {K_{24}}{R_2} + {K_{34}}{R_3} - {K_{44}}{R_4} = 0} $ | (9) |
利用式(6)—(9)求解元件的相对灵敏度,取平均值(仍然用K表示),得
| $ {K_i} = \frac{1}{4}\sum\limits_{j = 1}^4 {{K_{ji}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (i = 1,2,3,4) $ | (10) |
这样求出的相对灵敏度将为确定值,大小均在1附近,仍然满足式(5)。根据式(10),最终计算出相对标定灵敏度。
在实际观测中,观测曲线并非一直平缓变化,有可能因干扰(干扰因素种类较多,有人为和非人为干扰)而发生突变。当曲线发生突变时,各元件就可能不符合自洽方程。为此,引入C95信度指标,描述钻孔应变数据的自洽程度。
| $ {C_{95}} = 1 - \frac{{m{S_c}}}{{m{S_a}}} = 1 - \frac{{\sum\limits_{{N_{95}}} | ({S_1} + {S_3}) - ({S_2} + {S_4})|}}{{\frac{1}{2}\sum\limits_{{N_{95}}} | ({S_1} + {S_3} + {S_2} + {S_4})|}} $ | (11) |
其中,C95为四分量钻孔应变观测信度,表示观测元件的自洽程度;C95和N95的脚标“95”表示去掉5%的“坏点”,用剩余95%的数据进行统计;mSc为去掉5%的“坏点”的剩余95%差应变数据进行累加并求平均的均值;mSa为去掉5%的“坏点”的剩余95%和应变数据进行累加并求平均的均值。对于分量钻孔应变观测而言,C95是描述自洽程度的关键指标,当数据信度值较高时,就说数据是可靠的。
2 计算结果采用邱泽华(2017)提出的自洽信度指标C95信度值,用以评价佘山台四分量钻孔应变仪4个元件的自洽程度。选取2013—2018年佘山钻孔应变观测数据,采用邱泽华(2017)提出的变化矫正和差分矫正方法,以不同时间尺度,计算C95信度指标。
2.1 按月进行对比计算收集佘山台2013年1月至2018年8月共计68个月的数字化钻孔应变观测资料,运用Matlab,对原始观测值、差分值进行对比计算,得到K1、K2、K3、K4及矫正前后的C95信度,结果见表 1(因数据量过大,仅给出2013年度月尺度实地相对标定计算结果)。
| 表 1 变化值、差分值月尺度实地相对标定和数据矫正结果 Table 1 Results of field relative calibration and data correction for original values and difference values at a monthly scale |
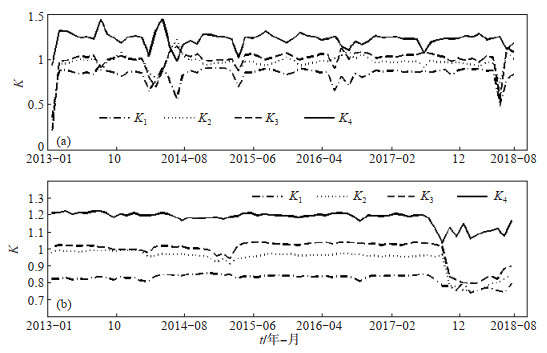
选取佘山台2013—2018年四分量钻孔应变原始观测数据(变化值)及差分值,代入式(10),求得2组K1、K2、K3、K4及矫正前后的C95信度指标,据所得灵敏度系数K值,绘制相对灵敏度变化趋势,见图 1。由图 1可见:①各元件相对灵敏度系数K值变化趋势相对平稳,个别月波动较大(观测系统故障,导致观测数据缺记或者产生台阶突跳);②K2和K3在数值1上下波动,K1<1,维持在0.82上下,K4>1,均值在1.2上下波动;③利用原始数据计算的元件相对灵敏度系数,变化趋势相对稳定;④差分值计算的相对灵敏度系数,2017年11月起,整体出现大幅度变化,该现象值得进一步研究。
|
图 1 变化值、差分值月尺度相对标定结果 (a)变化值实地标定;(b)差分值相对标定 Fig.1 Relative calibration results for original values and difference values at a monthly scale |
由表 1、图 1可知:K1和K4偏离1较大,已超出正常工作范围,需先行矫正2组观测数据,方可进行下一步分析。
采用变化值及差分值矫正前后的C95信度指标(表 1),绘制柱状图,结果见图 2、图 3,其中图 2给出各元件变化矫正前后C95信度柱状,图 3给出各元件差分矫正前后C95信度柱状。

|
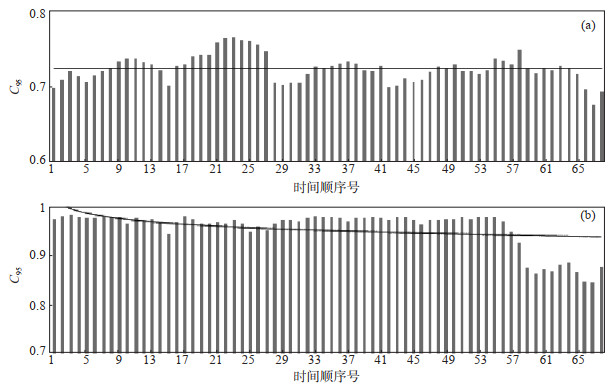
图 2 各元件变化值月尺度矫正前后信度值C95 (a)矫正前;(b)矫正后 Fig.2 The reliability index of C95 for the original values of each component before and after correction |
|
图 3 各元件差分值月尺度矫正前后信度值C95 (a)矫正前;(b)矫正后 Fig.3 The reliability index of C95 for the difference values of each component before and after correction |
由图 2可见:①矫正前,C95信度指标约0.7;其中有6个月的C95<0.4;②采用变化值矫正方法予以矫正,信度C95基本提高至0.95,接近1,但有3个月的C95<0.7,调查发现,当月出现数采、电源等故障现象,导致观测数据出现大面积缺失及台阶突跳。
由图 3可见:①经差分矫正,C95信度平均值从0.724 6提升至0.956 7;②2013年1月至2017年9月,C95信度稳定在0.95以上,2017年10月后下降至约0.85,可能是因为,各元件灵敏度系数突然发生变化,导致C95信度指标整体下降。
2.2 按年进行对比计算选取佘山台2013—2018年共计6年的数字化钻孔应变观测资料,运用Matlab,分别使用变化值(原始观测值)、差分值进行计算,得到K1、K2、K3、K4及矫正前后的C95信度,结果见表 2。将所得数值代入式(10),按年度分别求得6组K1、K2、K3、K4元件相对灵敏度系数及矫正前后C95信度指标,并绘制元件相对灵敏度变化趋势,结果见图 4。
| 表 2 2013—2018年变化值、差分值年尺度实地相对标定和数据矫正结果 Table 2 Results of field relative calibration and data correction for originalvalues and difference values at an annual scale from 2013 to 2018 |
|
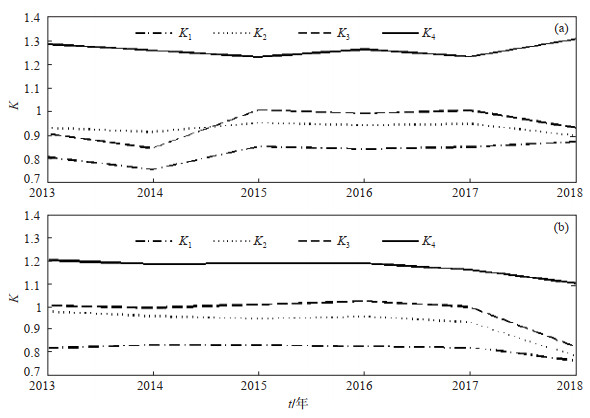
图 4 2013—2018年变化值、差分值年度相对标定结果 (a)变化值;(b)差分值 Fig.4 Relative calibration results for original values and difference values at an annual scale from 2013 to 2018 |
由图 4可见,在使用变化值计算的各元件相对灵敏度系数中,K1维持在0.76—0.87、K2维持在0.90—0.95、K3维持在0.85—1.01、K4维持在1.23—1.31,波动较大;而利用差分值计算得到的各元件相对灵敏度,波动幅度较小,更稳定。
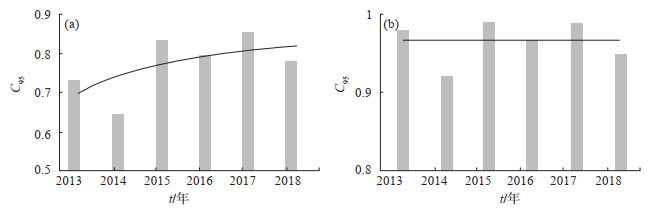
利用表 2中给出的变化值及差分值矫正前后的C95信度指标,绘制2类数据的C95柱状图,结果见图 5、图 6,其中图 5为变化值矫正前后的C95柱状图,图 6为差分值矫正前后的C95柱状图。由图 5可见,变化值矫正前C95信度指标在0.6—0.85范围波动,2014年度C95信度偏小;矫正后信度值C95>0.9,接近1。由图 6可见,变化值矫正前C95信度0.7—0.75范围波动;矫正后C95信度值在2013—2017年均大于0.9,2018年度仅0.868 3。
|
图 5 变化值年度矫正前后C95 (a)矫正前;(b)矫正后 Fig.5 The C95 for original values before and after annual correction |
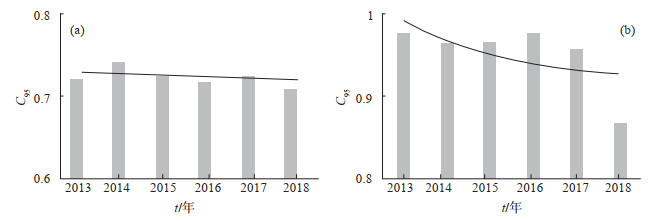
|
图 6 差分值年度矫正前后C95 (a)矫正前;(b)矫正后 Fig.6 The C95 for difference values before and after annual correction |
由表 2、图 5、图 6可知,采用钻孔应变观测年度变化值(原始值)和差分值进行数据矫正,变化值矫正后的C95信度指标值较高,表明在更长时间尺度下,利用原始值所得各元件灵敏度系数K值进行数据矫正,矫正后观测资料质量更高。
3 结论通过对钻孔应变观测数据的实地相对标定计算,发现佘山台四分量钻孔应变仪灵敏度系数K1和K4均偏离1较多,未矫正前C95自洽信度低于0.75。据邱泽华(2017)提出的变化矫正及差分矫正方法,以不同时间尺度,对佘山台钻孔应变观测数据进行实地标定并矫正。
(1)按月进行矫正计算时,矫正前C95<0.6,属“坏点”较多月份,采用差分矫正,可去除突跳和台阶点,平滑曲线,有效提高C95信度指标;对于矫正前C95>0.7的观测月,因该月观测资料质量良好,采用变化矫正方法效果更理想。
(2)按年对观测资料进行矫正时,采用变化矫正效果更优。
阚宝祥, 邱泽华, 唐磊. 2007. 泰安台钻孔差应变观测的实地标定[J]. 大地测量与地球动力学, 27(6): 119-123. |
柳忠旺, 侯炳正, 常兴, 等. 2014. 海原小山四分量钻孔应变观测相对标定和异常判定[J]. 防灾减灾学报, 30(4): 13-19. |
邱泽华, 石耀霖, 欧阳祖熙. 2005. 四分量钻孔应变观测的实地相对标定[J]. 大地测量与地球动力学, 25(1): 118-122. |
邱泽华. 2017. 钻孔应变观测理论和应用[M]. 北京: 地震出版社.
|
吴立辛, 张立强, 李国斌, 等. 2010. 海原台四分量钻孔应变观测的相对标定及资料应用[J]. 地震研究, 33(4): 318-322. DOI:10.3969/j.issn.1000-0666.2010.04.011 |
易志刚, 邱泽华, 宋茉. 2007. 钻孔体应变观测资料的实地校正[J]. 地震, 27(3): 117-123. |
 2020, Vol. 41
2020, Vol. 41

