2. 中国江苏 210000 南京市地震局;
3. 中国江苏 211100 南京市江宁地震台
2. Nanjing Earthquake Agency, Jiangsu Province 210000, China;
3. Jiangning Seismic Station, Jiangsu Province 211100, China
钻孔应变观测是研究地壳运动的主要观测手段,在地震地球物理观测中占有重要地位(苏恺之等,2003)。将仪器安装于近百米以至数千米的地下,能明显降低地表的各种干扰,并具有较好的动态观测性能与耐震性能,易于选点布设成网和维护管理。近年来,该仪器布设方法日益受到各国重视,发展速度较快。
我国钻孔应变观测已有40年历史,以体积式和分量式2种钻孔仪器为主,观测频带为0—3 000 Hz,观测精度达10-10,可记录到各种应变潮汐及非应变信息。钻孔应力—应变方法在地震监测预报中具有独特优势,可通过测量钻孔孔径的变化,直接或间接测量地壳应力—应变状态的相对变化,观测到与地震的孕育、发生直接相关的应力—应变信息(池顺良等,2009)。对于钻孔应变资料观测的可靠性和稳定性,邱泽华等(2010)、池顺良等(2014)、侯跃伟等(2015, 2018)诸多研究者做了许多有意义的工作,如:邱泽华等(2005)从分量钻孔观测的理论模型入手,提出实地标定的反演方法,这是一种利用理论固体潮来求解换算所需耦合系数的方法;唐磊等(2015)提出钻孔应变观测数据不同时间尺度的自检方法;田韬等(2014)应用应力函数法研究耦合介质弹性性质变化对钻孔耦合系数的影响。本文在前人对钻孔应变资料自检、可靠性分析的理论基础上,通过Venedikov调和、相对标定等方法,分析江宁地震台2009年以来四分量钻孔应变资料的可靠性。
1 台站观测条件 1.1 地质构造江宁地震台(下文简称江宁台)位于南京市江宁区禄口镇石埝村,测区所处地貌属秦淮河冲积平原,地形开阔平坦,高差小于2 m。地表为第四系冲积层覆盖,主要成分为砂砾、淤泥质砂质粘土及粉砂、粘质砂土。根据地矿部门提供的区测资料反映,测区及周边地区第四系以下地层为侏罗系上统龙王山组(J3L),主要岩性为灰紫色凝灰角砾岩,覆盖层厚达392 m,下伏象山群(J1-2)灰黄色泥质粉砂岩。测区所在构造单元为溧水中生代火山岩盆地,其形成和发育与南京—湖熟断裂、方山—小丹阳断裂关系较为密切。
1.2 仪器安装江宁台属国家一类形变和测震观测台站,观测环境良好。该台分量钻孔应变于2006年12月试观测,钻孔深度50.09 m,其中:9.84 m以上为第四系粉质粘土;9.84—14.62 m为风化安山岩;14.62—50.09 m为致密块,在此层设置YRY-4分量钻孔应变仪,钻孔内同时配备水位和气压辅助观测探头。为防止地表或地下水进入观测井,地面至45 m深采用直径130 mm的标准钢套管保护,岩壁与钢套管间用水泥浆压力密封,将护井套管与岩壁精密固结。仪器安装前实测井孔状况,参考钻孔资料,用钢丝绳吊127 mm孔径测试器,下井深度50.09 m(下到观测井底部)。钻孔应变仪有4个测向,即NS、EW、NE和NW向,其中1号元件方位角-50°,2号元件方位角-5°,3号元件方位角40°,4号元件方位角85°。
2 可靠性评价与分析 2.1 连续率和年变幅分析江宁台分量钻孔应变仪采样率为每分钟记录一次观测数据,统计2009—2018年该台钻孔应变观测资料的年变幅、连续率,见表 1。
| 表 1 江宁台2009年以来钻孔应变年变幅和连续率统计 Table 1 The annual variability amplitudes and continuity rates of borehole strain records at Jiangning Seismic Station since 2009 |
在连续率上,2009—2018年,除断电、数据采集器出现短暂故障外,江宁台钻孔应变观测曲线断记较少,整体连续率达98%以上,全年断记不超过4 d,符合地壳形变技术规范要求。
在年变幅上,钻孔应变4个测向处于稳定的调整阶段,年变幅各不相同。绘制2009—2018年钻孔应变长趋势观测曲线,见图 1,可知:4个分量呈整体压性变化,其中NW分量变化幅度和下降速率最大;2012年、2014年和2017年4个测项出现3次明显的准同步阶跃,阶跃幅度不同。调查发现,2012年6月,江宁台数据采集器电源出现故障,更换仪器后观测曲线出现同步阶跃;2014年3月23日,江宁台地电阻率保护试验项目在距钻孔应变井10 m、20 m处开钻2个钻孔,对四分量应变观测造成明显干扰,NE、NW分量变化幅度明显,约为年变化幅度的5.3和3.4倍;2017年9月,受S340省道施工影响(距台站约200 m),江宁台钻孔应变4个测道出现明显阶跃,变化幅度和下降速率较大。

|
图 1 江宁台2009—2018年钻孔应变长趋势观测曲线 Fig.1 The long-term trend of borehole strain at Jiangning Seismic Station during 2009-2018 |
对江宁台应变观测值进行Venedikov调和分析。为了使数据具有连续性和完整性,基于理论值外推或内插进行缺值处理,补齐数据;根据扣除固体潮影响的漂移曲线,先区分随机错数和掉格,对随机错数采用平滑方法予以改正。对大于限定值的掉格,采用平推基线法加以改正(侯跃伟等,2018)。在计算潮汐参数时,为了消除干扰数据对分析结果的影响,可采取以下步骤:采用Nakai拟合方法,以48 h间隔(维尼迪科夫数字滤波器间隔)逐次做拟合检验,并统计拟合方差限值,根据各组方差大小酌情取舍(李兴坚等,2015),使用Venedikov调和分析方法,对预处理后观测资料进行逐月调和分析,从而得到应变潮汐参数,结果见表 2。
| 表 2 江宁台Venedikov调和分析M2波潮汐因子及精度 Table 2 The Venedikov harmonic analysis of M2 wave tidal factors and accuracy at Jiangning Seismic Station |
由表 2可知,2009—2018年,江宁台分量应变M2潮汐因子为1.177 6—3.617 6,相对中误差<0.05,符合地壳形变观测技术规范要求。
2.3 相对标定分析在实际观测中,当某个测量元件格值出现明显系统偏差时,不会体现在中误差数值上。潮汐因子中误差大小尚不能充分论证钻孔应变观测资料的可靠性,需要对4个元件之间格值的一致性(是否存在系统偏差不一致现象)给予检查和纠正,称之为相对标定(高丽娟等,2015;邱泽华,2017)。设Si为用于计算应变变化的元件观测数据,Ri为需要矫正的观测数据,令
| $ {{S}_{i}}={{k}_{i}}{{R}_{i}} $ | (1) |
其中,ki待定,称为元件灵敏度矫正系数。
所谓相对实地标定就是要计算ki。将式(1)代入自洽方程,可得
| $ {{k}_{1}}{{R}_{1}}-{{k}_{2}}{{R}_{2}}+{{k}_{3}}{{R}_{3}}-{{k}_{4}}{{R}_{4}}=0 $ | (2) |
设4个元件中任意1个灵敏度矫正系数为1,将不同的3组观测数据代入式(2),得到3个方程后求解方程组,即可以求出其他3个矫正系数。对于大量不同数据,可以采用最小二乘方法予以统计,但计算结果存在缺陷,即除灵敏度矫正系数设定为1的元件,其他元件的矫正系数随观测数据不同而改变,需要寻求更好的方法。
定义kij = kj/ki(i,j=1,2,3,4),得到关于所有元件对称的4个灵敏度矫正系数。由此得到4个齐次的线性方程
| $ \left\{ \begin{matrix} {{k}_{11}}{{R}_{1}}-{{k}_{12}}{{R}_{2}}+{{k}_{13}}{{R}_{3}}-{{k}_{14}}{{R}_{4}}\text{=}0 \\ {{k}_{21}}{{R}_{1}}-{{k}_{22}}{{R}_{2}}+{{k}_{23}}{{R}_{3}}-{{k}_{24}}{{R}_{4}}\text{=}0 \\ {{k}_{31}}{{R}_{1}}-{{k}_{32}}{{R}_{2}}+{{k}_{33}}{{R}_{3}}-{{k}_{34}}{{R}_{4}}\text{=}0 \\ {{k}_{41}}{{R}_{1}}-{{k}_{42}}{{R}_{2}}+{{k}_{43}}{{R}_{3}}-{{k}_{44}}{{R}_{4}}\text{=}0 \\ \end{matrix} \right. $ | (3) |
其中,当i = j时,kij =1。重要的是,这里有12个未知数,而4个方程实际上来自同一个关系式,即自洽方程。每个方程要单独求解,且由于存在数据随机变化误差,各方程给出的解可能并不协调一致。
将4个方程给出的所有解取平均,得到所有元件的实用灵敏度矫正系数
| $ {{k}_{i}}=\frac{1}{4}\sum\limits_{j=1}^{4}{{{k}_{ij}}}\ \ \ \ \ \ \left(i=1, 2, 3, 4 \right) $ | (4) |
表 3列出2009—2018年江宁台分量钻孔应变元件相对矫正系数,可见4个分量矫正系数均在1上下,表明仪器出厂质量较好,安装过程无纰漏,观测数据可靠。
| 表 3 江宁台钻孔应变相对标定计算结果 Table 3 Relative calibration calculation results of Jiangning Seismic Station |
表 3中C95表示去掉5%的坏点,用剩余95%的数据进行统计,为四元件钻孔应变观测的信度,用来刻划观测的自洽程度。一般,比较自洽的观测数据信度应接近1。对于四元件钻孔应变观测而言,描述自洽程度的信度是一个关键指标。当数据信度较高时,就说数据是可靠的。
2.4 稳定性分析钻孔应变观测是,将应变传感器探头放入钻孔,使用特制水泥填充探头与周围介质之间的孔隙,将二者耦合起来,观测应变变化。钻孔应变观测值由(ε1+ε2)与(ε1 - ε2)两部分构成,其中(ε1+ε2)与面应变(面积)有关,(ε1 - ε2)与剪应变(形状)有关。
如图 2所示,沿θ方向安装的元件,直接观测该方向探头套筒内径的相对变化Sθ,即元件长度变化量与其长度之比。Sθ与ε1、ε2、φ的关系如下
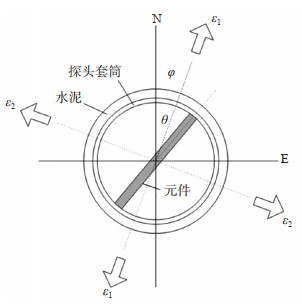
|
图 2 钻孔应变仪观测平面应变张量的原理模型 Fig.2 Principle model for observation plane strain tensor of the borehole strain gauge |
| $ {{S}_{\theta }}=A\left({{\varepsilon }_{1}}+{{\varepsilon }_{2}} \right)+B\left({{\varepsilon }_{1}}-{{\varepsilon }_{2}} \right)\cos 2\left(\theta -\varphi \right) $ | (5) |
其中,ε1为最大主应变,ε2为最小主应变,φ为应变主方向;A、B为待定常数,称为耦合系数。A、B的大小与套筒的材料和尺寸、水泥的材料和尺寸以及周围岩石性质等关系复杂。这里的ε1、ε2、φ是足够远处的应变,一般认为,只要与钻孔间的距离大于10倍钻孔直径即可(邱泽华,2017)。
与相对标定相比,进行四分量钻孔应变观测实地绝对标定需要真实应变值,目前无法得到,一般用地球理论应变固体潮表示“真实的应变”(邱泽华,2017)。实地标定反演使用的理论固体潮,只考虑由太阳和月亮运行引起的应力变化,不考虑其他因素(例如海洋潮汐、地形等)影响。为进一步探讨江宁台四分量钻孔应变观测稳定性,使用拟合观测和理论观测小时值进行差分,结果见图 3,其中Dsa和DSs分别表示观测面应变和观测最大剪应变的小时值差分,DεaT和DεsT分别表示理论面应变的小时值差分和理论最大剪应变的小时值差分。由图 3可见,观测面应变小时值差分曲线与耦合系数A的变化基本同步,观测最大剪应变的小时值差分曲线与耦合系数B的变化基本同步,通过线性拟合,计算得到:耦合系数A均值为0.590 4,标准差为0.307 5,波动程度较低;耦合系数B均值为1.222 5,标准差为0.866 5,波动程度较高。B值大于A值,符合钢制套管的变形特征,即形变易变而面积难变。
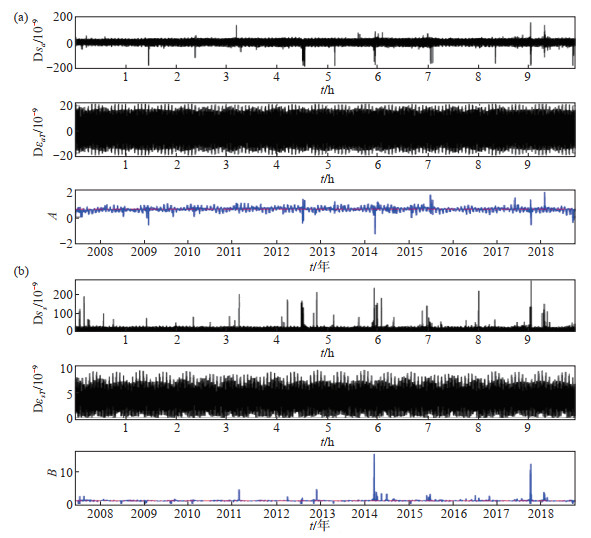
|
图 3 江宁台钻孔应变观测绝对实地标定结果 Fig.3 Field calibration of borehole strain observation at Jiangning Seismic Station |
耦合系数A、B为常数,可以通过以下2种方法获得:①根据观测的理论模型,设法获得围岩、水泥和探头套筒的弹性参数,根据弹性力学模型公式,求出A、B值;②通过已知量(理论固体潮)比较确定耦合系数,即文中所使用的方法。由图 3可见,江宁台钻孔应变耦合系数A、B值变化范围基本稳定,但受台站施工等因素影响,2014年A、B值出现明显异常,耦合系数A甚至出现负值,表明钻孔应变观测受到明显干扰。因此,可利用耦合系数A、B值评价系统稳定性特征。
3 结论基于江宁台2009—2018年钻孔应变观测资料,检验了YRY-4型四分量钻孔应变仪的可靠性,得出以下结论。
(1)江宁台钻孔应变观测资料完整,数据连续性较好,固体潮记录和地震波信息清晰。
(2)Venedikov调和相对标定结果显示,江宁台M2潮汐因子值为1.177 6—3.617 6,观测精度高,符合地壳形变观测技术规范要求。
(3)关于江宁台钻孔分量应变元件4个分量相对矫正系数均在1上下,表明仪器出厂质量较好,安装规范,观测数据可靠。受施工影响,2014年江宁台应变仪实地绝对标定耦合系数A值和B值出现明显突跳,其他年份保持在恒定水平,进一步说明该台钻孔应变观测系统的稳定性。
钻孔应变具有观测精度高、连续性和稳定性好等优点,但易受外部环境干扰,影响观测数据质量,需要进一步加强地震台站的运行维护,提高社会和公众认知度,加大地震台站观测环境保护力度。
致谢: 本研究使用了邱泽华研究员撰写的Matlab相关程序,在此表示感谢。
池顺良, 池毅, 邓涛, 等. 2009. 从5.12汶川地震前后分量应变仪观测到的应变异常看建设密集应变观测网络的必要性[J]. 国际地震动态, 11061106(1): 1-13. DOI:10.3969/j.issn.0253-4975.2009.01.001 |
池顺良, 张晶, 池毅. 2014. 汶川、鲁甸、康定地震前应变数据由自洽到失洽的转变与地震成核[J]. 国际地震动态, 11061106(12): 3-13. DOI:10.3969/j.issn.0235-4975.2014.12.003 |
高丽娟, 谢姆斯叶·艾尼瓦尔, 邢喜民, 等. 2015. 用超限率分析法提取钻孔倾斜地震前兆异常信号[J]. 大地测量与地球动力学, 35(4): 707-710. |
侯跃伟, 赵兵, 田韬. 2015. 基于Daubechies小波分析的南京数字化钻孔形变震前变化特征研究[J]. 震灾防御技术, 10(2): 388-396. |
侯跃伟, 郑建华, 夏孝田. 2018. 高淳台YRY-4钻孔分量应变观测数据突变(阶跃)及异常特征分析[J]. 国际地震动态, 11061106(5): 20-27. DOI:10.3969/j.issn.0253-4975.2018.05.005 |
李兴坚, 许玉红, 史继平, 等. 2015. 高台地震台钻孔应变观测资料的分析[J]. 地震地磁观测与研究, 36(2): 58-63. DOI:10.3969/j.issn.1003-3246.2015.02.011 |
邱泽华, 石耀霖, 欧阳祖熙. 2005. 四分量钻孔应变观测的实地相对标定[J]. 大地测量与地球动力学, 25(1): 118-122. |
邱泽华, 张宝红, 池顺良, 等. 2010. 汶川地震前姑咱台观测的异常应变变化[J]. 中国科学:地球科学, 40(8): 1031-1039. |
邱泽华. 2017. 钻孔应变观测理论和应用[M]. 北京: 地震出版社.
|
苏恺之, 李海亮, 张钧, 等. 2003. 钻孔地应变观测新进展[M]. 北京: 地震出版社.
|
唐磊, 吕品姬. 2015. 钻孔四分量应变观测数据不同时间尺度的自检分析[J]. 大地测量与地球动力学, 35(3): 525-528. |
田韬, 杨军, 郝永亮, 等. 2014. 原地应力对钻孔应变耦合系数的影响分析[J]. 地震研究, 37(3): 419-425. DOI:10.3969/j.issn.1000-0666.2014.03.015 |
 2020, Vol. 41
2020, Vol. 41

