0 引言

地球周围存在的磁场称为地磁场，按场源位置划分为内源场和外源场。其中，内源场包括源于地核的基本场、源于地壳磁性岩石的地壳场以及外部变化磁场在地球内部的感应磁场；外源场源于地表以上的空间电流体系（张建国等，2007）。地磁学研究是以地磁场观测为前提的科学，地磁场基础观测数据直接或间接用于研究地球基本磁场及其长期变化，不仅可以通过地磁观测获取地球内部结构信息和地球外部空间电流体系乃至太阳活动的信息，还可为国防、航天、测绘、邮电通讯、物探等国家战略核心部门提供可靠、完整、连续、准确的数据信息（熊仲华等，1997）。此外，研究表明，地震的孕育和发生伴随着地下介质电磁性质的改变和电磁场的变化（包括电磁波辐射）（徐文耀，2003）。连续完整、准确、可靠的地磁数据，不仅为地磁学及相关学科的科学研究服务，更是为地震预报提供基础数据。

随着经济建设的飞速发展，各种干扰因素不断出现，高速公路、地铁、直流输电、大型变压器等均会对地磁观测产生致命影响（沈红会等，2005），地磁数据记录的缺失及错误时有发生。数据缺失不仅影响数据的完整性，也会对数据分析造成较大影响。因此，在数据已经缺失或错误的情况下尽可能不失真的重构观测数据，保证数据的可用性，对于地磁数据分析而言具有重大意义（姚休义等，2016）。

空间加权法对数据重构具有显著优点，但以往研究多未考虑磁暴影响。当磁暴发生时，所有地磁要素均会发生剧烈变化。其中，水平分量H变化最大，垂直分量Z、磁偏角D也必然受到影响（袁桂平等，2018）。基于此，本文基于云南省地磁台站观测记录的地磁分数据，利用空间加权法进行数据重构，并分析重构结果精度与磁暴指数（D_st）之间的关系，旨在提高该方法对地磁数据重构分析的精度及真实性。

1 数据重构原理与方法

地球表面局部区域内若干点的地磁场变化主要受同源影响并具有相似性，两地记录的地磁场同一要素变化，具有较强和较稳定的空间相关性（朱兆才，1989；冯志生等，2005）。因此，基于空间加权法，利用假设缺失数据的台站（目标台）附近的台站数据，进行权重分配，并重构其所缺失的数据。

1.1 数据重构原理

基于地磁空间相关性提出空间加权法。在不考虑台站数据质量的情况下，假设各台站间相关系数、权重因子与其间距呈一次反比关系，通过建立一次线性拟合方程，确定各台站间的拟合系数、参考台的权重因子，计算出目标台的重构数据（姚休义，2015）。

然而，在地磁相对观测中，由于各台站地磁观测仪器存在定向差异，地磁观测数据在形态及相似数值上差别较大（胡星星等，2010；胡秀娟等，2014）。为避免仪器定向差异所导致的数据量级差别较大而造成数据重构误差较大的现象，需要在数据重构前将各台站数据进行归一化处理。归一化公式为

$ {{y}_{ij}}=\frac{{{B}_{j}}-{{B}_{\min }}}{{{B}_{\max }}-{{B}_{\min }}} $

(1)

其中：y_ij为第i个台站的第j个归一化数据，B_j为归一化前第j个数据，B_min、B_max分别为非缺失记录数据中的最小值和最大值。

权重因子及重构数据计算公式为

$ \sum\limits_{i=1}^{N}{{{W}_{i}}}=1 $

(2)

$ {{W}_{1}}\cdot {{R}_{1}}={{W}_{2}}\cdot {{R}_{2}}=\ldots ={{W}_{N}}\cdot {{R}_{N}} $

(3)

$ {{Y}_{j}}=\sum\limits_{i=1}^{N}{{{W}_{i}}\cdot {{X}_{ij}}+r} $

(4)

式中，W_i为第i个参考台台站的权重因子，R_i为两台站之间的距离，X_ij为第i个参考台的第j个数据，Y_j为第j个归一化后的重构数据，r为残差项。由式（2）—（4）即可求出归一化重构数据Y_j，将Y_j带入式（1）可反算重构数据B_j。

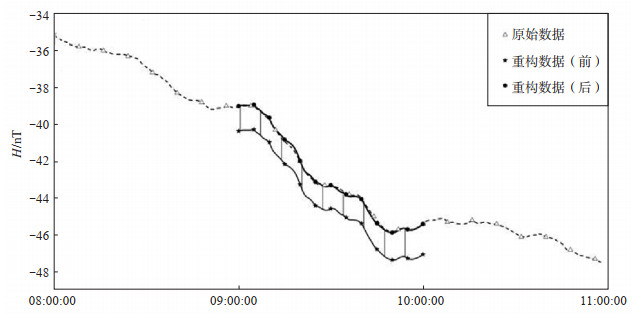
1.2 台阶改正

由于日变形态差异所造成的相位延时，对数据重构有较大影响，重构前后的数据形态表现为首尾台阶差。为保证数据的连续性，采用线性台阶改正方式进行台阶改正（图 1）。

线性台阶改正公式为

$ {{B}_{j}}^{\prime }={{B}_{j}}+\frac{\text{d}{{B}_{2}}-\text{d}{{B}_{1}}}{M}\times j-\text{d}{{B}_{1}}\ \ \ \ \ j=1, 2, 3, \ldots, M $

(5)

式中，${{B}_{j}}^{\prime }$为最终重构结果，B_j为归一化前第j个数据，dB₁为加权后首台阶，dB₂为加权后尾台阶，M为缺失的数据数。

2 数据重构精度与D_st指数相关性分析 2.1 地磁空间相关性

以数据质量较好的通海台（THJ）、楚雄台（CHX）、永胜台（YOS）、丽江台（LIJ）为参考台，以景谷台（JIG）、勐腊台（MLA）、富源台（FUY）、西盟台（XIM）、盈江台（YIJ）、马关台（MAG）、云龙台（YUL）为目标台，统计台站相对地磁记录数据的相关性，结果见表 1。其中，景谷台（JIG）、云龙台（YUL）全年缺数较多，此处不做统计。由表 1可见，参考台与目标台之间的地磁观测数据相关系数均大于0.9，具有较高的相关性。

2.2 计算结果

假设目标台某天某时段原始数据缺失或错误，由于参考台和目标台数据相关性较高（表 1），可利用空间加权法对目标台记录数据进行重构。

假定在利用空间加权法进行数据重构时不考虑地球磁场因素影响，利用绝对残差（error）计算其重构精度。绝对残差e计算公式为

$ e=\frac{\sum{\left| f\left(n \right)-\hat{f}\left(n \right) \right|}}{N}\ \ \ \ \ \ n=1, 2, 3, \ldots $

(6)

式中，-f为地磁台站的原始观测数据，|为重构后的数据，N为缺失数据数。

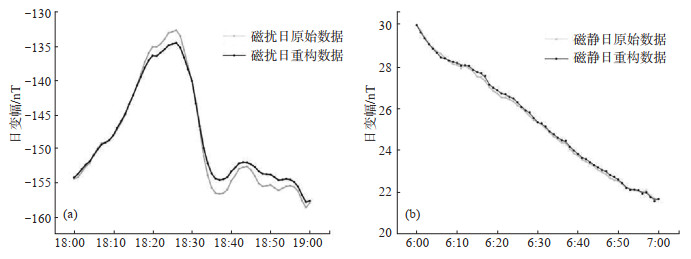
在利用空间加权法进行地磁分数据重构过程中发现，计算结果的精度与磁暴现象（地磁静扰）密切相关，磁静日与磁扰日重构精度不相同，结果见图 2。由图 2清晰可见，在磁扰日时，重构数据与真实观测数据之间误差较大；在磁静日时，真实观测数据与重构数据差异较小，数据可靠性较高。

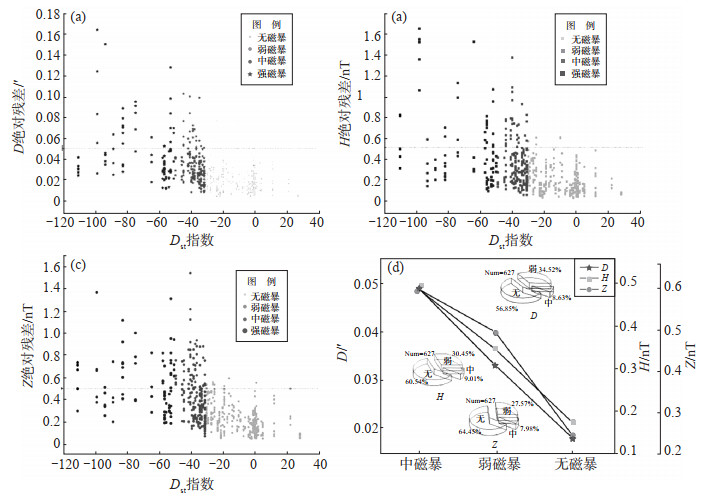
因此，需考虑磁暴对地磁重构数据的影响。磁暴是一种剧烈的全球性地磁扰动现象，通常用K_p指数或D_st指数来描述，其中，K_p指数每3小时计算一次，D_st指数每小时计算一次。从时间尺度而言，D_st指数能更好地描述磁场活动性对数据重构的影响（王仁明等，2011）。D_st指数描述了西向环电流在赤道附近引起的地磁场扰动情况。一般认为，-50＜D_st ≤-30为弱磁暴、-100＜D_st ≤-50为中等磁暴、-200＜D_st ≤-100为强磁暴（刘振兴，2005；徐文耀，2009；赵旭东等，2019）。文中分别对2016年度各地磁台在平静日、弱磁暴、中等磁暴、强磁暴时的地磁记录数据进行研究，利用空间加权法，统计在不同D_st指数情况下重构数据精度的变化，结果见图 3。

2.3 结果分析

以2016年度各台地磁观测数据为例，统计得到不同磁扰强度下（D_st指数不同）重构数据总次数为632次，其中无磁暴346次，弱磁暴204次，中等磁暴77次，强磁暴5次。统计发现，当D_st＞-30时，D、H、Z三分量的平均绝对残差值分别是0.018′、0.17 nT、0.19 nT；当-50＜D_st ≤ -30时，D、H、Z三分量的平均绝对残差值分别是0.033′、0.34 nT、0.43 nT；当-100＜D_st ≤ -50时，D、H、Z三分量的平均绝对残差值分别是0.049′、0.48 nT、0.53 nT[图 3(d)]。

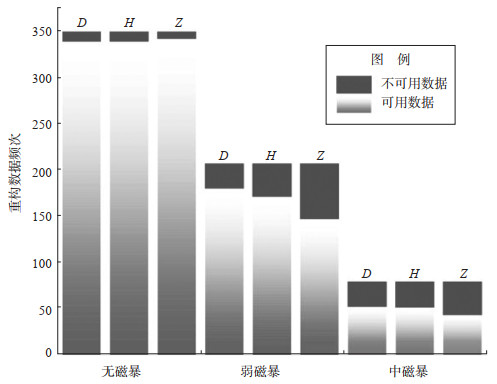
在日常数据处理中，通常把一阶差分高于0.05′或0.5 nT的数据视为干扰数据，在0.05′或0.5 nT以内的数据视为可用数据。因此，以0.05′或0.5 nT为分界线。当D_st＞-30时，小于0.05′的D分量绝对残差值占比97.1%，小于0.5 nT的H分量绝对残差值占比97.1%，小于0.5 nT的Z分量绝对残差值占比97.9%。当-50＜D_st ≤ -30时，小于0.05′的D分量绝对残差值占比87.3%，小于0.5 nT的H分量绝对残差值占比82.8%，小于0.5 nT的Z分量绝对残差值占比71.1%。当-100＜D_st ≤ -50时，小于0.05′的D分量绝对残差值占比66.2%，小于0.5 nT的H分量绝对残差值占比64.9%，小于0.5 nT的Z分量绝对残差值占比54.5%（图 4）。

利用该统计结果（图 4）进行分析，笔者认为，未发生地磁扰动时（D_st＞-30），小于0.5 nT的D、H、Z三分量绝对残差值占比均在97%以上，说明重构后的数据可信度较高，重构精度较高。当发生弱磁暴、中等磁暴时，D、H、Z三分量绝对残差值在增大，数据可信度减小。整体而言，D、H、Z三分量数据重构精度均随着D_st指数绝对值的增大而减小，总体呈负相关。因此，在利用空间加权法对地磁数据进行重构前，应对异常当日的磁场活动水平进行评估，以增加重构数据的真实度、可信度。

3 结论与讨论

利用空间加权法，对干扰台站缺失或错误的数据进行重构，统计在不同磁扰强度下数据重构精度的影响，得出以下结论。

（1）磁扰日重构数据残差高于磁静日。

（2）随着D_st指数绝对值的增大，数据重构残差增大，重构精度减小，总体呈线性关系。

（3）无磁暴发生时，小于0.5 nT的D、H、Z三分量重构数据与原始数据的绝对残差值占比均在97%以上，重构后的数据可信度较高，重构精度较高。当发生弱磁暴、中等磁暴时，D、H、Z三分量重构数据与原始数据的绝对残差值随着D_st指数绝对值的增大而增大，重构精度减小。

统计发现，无磁暴时，重构数据与原始数据的残差较小，重构精度较高，可利用此方法来填补缺失或错误的数据；有磁暴发生时，重构数据精度会受到影响，空间加权法重构数据可信度随着D_st指数绝对值的增大而降低。因此，在利用空间加权法进行数据重构时，应注意磁场活动水平强弱。同时，可以结合其他地磁数据重构方法，比如：等效源方法、神经网络方法等进行综合研究。需要说明的是，磁扰日也可以利用此方法进行数据重构，只是算法需要进一步改进，去除干扰，提高信噪比，以减小磁扰日重构数据残差，提高重构数据精度。