及时、准确的地震定位,对于地震应急救援、地震预测预报有着重要意义。然而在日常地震监测中,由于诸多非天然震动源的干扰,地震记录的准确性受到一定程度影响。在众多非天然干扰源中,爆破的记录波形与天然地震类似,需要花费大量时间进行识别与排除,工作效率受到影响,而利用自动分类技术完成爆破事件的自动识别与剔除,不仅可以大幅提升工作效率,还能有效保障地震目录质量,为地震活动性预测、地震危险性评估、地震预报等工作提供高质量数据。
对地震与爆破事件特征的研究始于20世纪50年代初期,国内外众多专家学者对地震事件的分类技术开展了广泛和深入的研究,形成了根据发震时刻、震中位置、初动方向、初动振幅等特征进行事件类型判别的经验方法,以及使用波谱差异特征(张萍等,2005)、波形频率特征(王婷婷等,2014;Beccar-Varela et al,2016)、振幅衰减特征(王婷婷等,2015)、震相幅值比特征(Pasyanos,2010;杨芳等,2016)、多重分形特征(Lyubushin et al,2013)和使用多特征进行统计分类的方法(Fäh et al,2002;Yılmaz et al,2013)。
随着地震波形特征研究的不断深入,以及模式识别技术的快速发展,模式识别技术开始用于地震事件自动分类研究,如:边银菊等(2012)、张博等(2014)使用决策的方法,根据特征参数差异进行投票,实现事件分类;Kuyuk等(2014)使用线性聚类的方法,根据不同事件的特征参数,对事件进行聚类识别。近年来,使用机器学习方法进行事件分类成为一个趋势,如黄汉明等(2010)、毕明霞等(2011)使用支持向量机,将事件特征作为输入向量,进行监督学习并实现分类;Kuyuk等(2012)使用K均值和高斯混合模型进行无监督学习,实现对伊斯坦布尔地震的分类。
尽管上述地震事件识别方法均取得较好效果,能够将爆破事件从地震事件中有效排除,但诸多方法通常只针对一个地区的地震与爆破事件特征差异进行研究。由于不同地区的地层构造、仪器类型参数、分析记录软件、背景噪声等存在差异,记录的事件波形特征并不完全一致。在不同地区使用同一种地震事件分类方法时,需要重新分析当地的大量事件波形,重新总结特征参数的分类标准,导致分类技术的推广在一定程度上受到限制。
本研究的主要目标是,提出一种具有较高准确率且能够对事件特征参数自主完成学习的分类方法。该方法源于地震与爆破事件的能量在频谱分布上存在差异,具体步骤如下:提取2类事件的P波和S波在不同频带上能量的分布特征,运用径向基函数(Radical Basis Function,简写为RBF)神经网络技术,完成对2类事件参数特征的学习,建立神经网络,实现事件的自动分类。
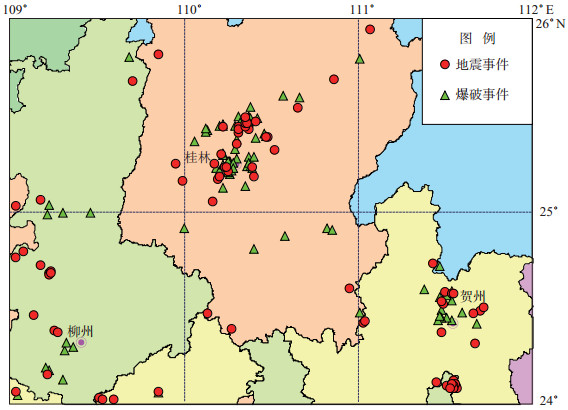
1 数据选择以桂林及周边地区为研究区域(109°—112°E,24°—27°N),采用2014—2017年广西地震台网中心记录的68个地震与74个爆破事件波形作为研究数据。其中,爆破与地震事件的震级在ML 1.0—3.0,震源深度小于10 km,震中分布见图 1。
|
图 1 地震与爆破事件分布 Fig.1 Earthquakes and explosions distribution |
爆破产生的地震波,随着震中距增大,高频成分会被地表逐渐吸收(中国地震局监测预报司,2017)。地震波高频成分的变化将造成事件频谱能量分布特征的改变。因此,为了消除因震中距差异过大而造成的波形特征变化,同时保证P波和S波之间有足够的时间差,并确保提取频率特征时有足够样本数据,选用震中距在20—80 km、采样率为100 sps、波形记录清晰的事件。同时,为了降低不同分向波形记录差异的影响,只选用垂直分向记录,最终提取地震波形记录176条,爆破波形记录163条。
2 特征提取地震与爆破事件波形的频谱差异由二者震源机制差异造成。地震震源是剪切位错源,位于地下几千米甚至更深处。地震的破裂过程较长,产生的地震波经地下多层介质的反射、折射、散射等影响,频谱复杂,能量在各频段上分布比较均匀,波形持续时间长。与地震不同,爆破震源是瞬时膨胀的点源,通常位于地表,产生的地震波的传播路径介质比较单一,频带分布较窄,波形衰减快,能量集中(靳玉贞等,2015)。因此,在地震事件分类识别中,时频图和频谱图是常用的区分地震和爆破事件的有效工具。
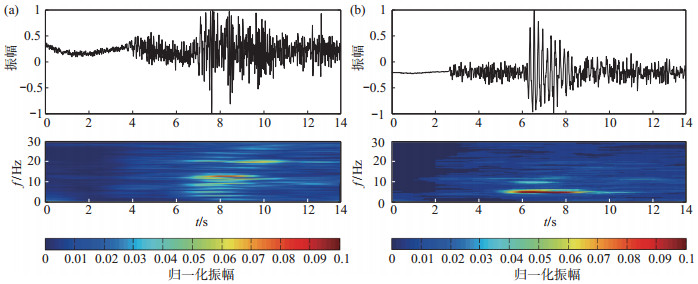
以兴安地震台记录的2015年7月29日桂林市辖区ML1.3地震事件(Δ = 26 km)和同年9月26日桂林市辖区ML 2.0爆破事件(Δ = 31 km)为例,对2次事件的垂向波形进行时频分析,其中原始波形经归一化处理,结果见图 2。由图 2可见,地震事件能量的频率分布范围广,优势频率在10 Hz上下;爆破事件能量的频率分布范围较窄,优势频率约5 Hz。
|
图 2 事件波形及时频分析 (a)地震;(b)爆破 Fig.2 Waveforms and spectrograms |
特征提取是一个从数据空间到特征空间变换的过程。因此,从大量原始数据中准确提取有效特征数据,是事件分类识别能否成功的关键所在。由于地震与爆破事件的能量分布在频带上有明显差异,因此,对事件波形进行多频带分解,可有效提取事件特征。
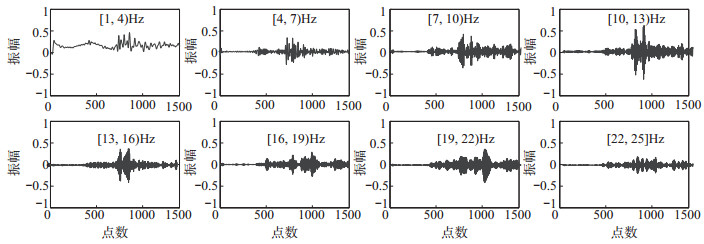
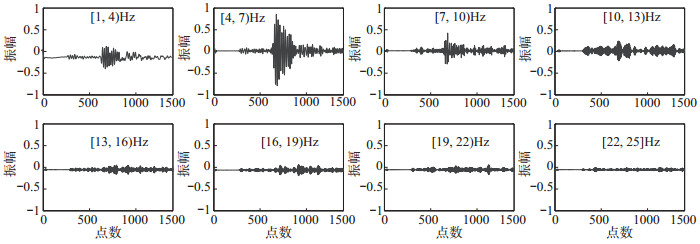
采用由无限脉冲响应(Infinite Impulse Response,简称IIR)数字滤波器构成的带通滤波器组,将事件波形过滤成带宽3 Hz、覆盖范围在1—25 Hz的窄带波形组(表 1)。选取1—25 Hz频率段的原因如下:①消除地脉动(频率<1 Hz)对事件识别的影响;②滤除非优势频率段的数据。2015年的地震和爆破事件示例窄带波形组见图 3、图 4。
| 表 1 数字滤波器频带范围 Table 1 Frequency-bands used for signal filtering |
|
图 3 2015年7月29日ML1.3地震事件窄带波形组 Fig.3 Waveforms of narrow frequency bands for the ML 1.3 earthquake on July 29, 2015 |
|
图 4 2015年9月26日ML 2.0爆破事件窄带波形组 Fig.4 Waveforms of narrow frequency bands for the ML 2.0 explosion on September 26, 2015 |
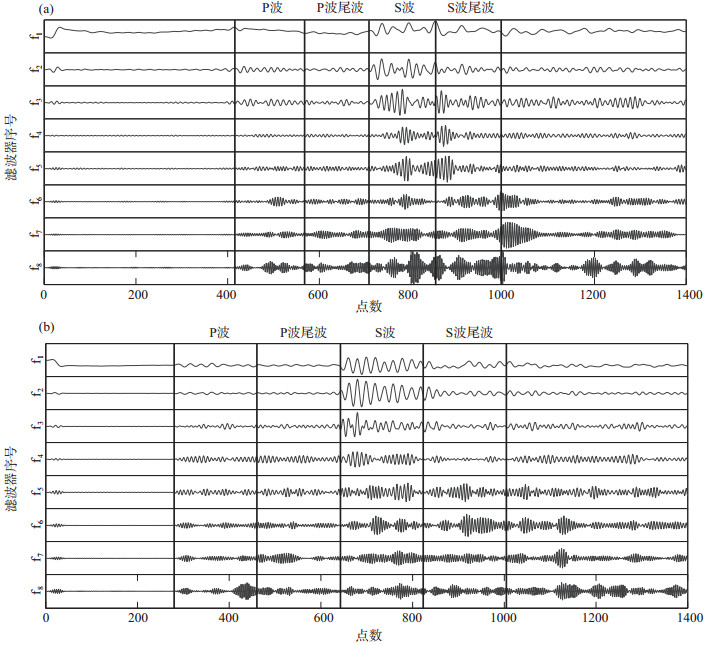
事件波形分解完成后,提取各窄带波形组中的P波、P波尾波、S波、S波尾波的波形数据用于计算特征值。图 5分别展示了2015年地震与爆破事件示例的窄带波形组,纵坐标f1—f8分别对应表 1中滤波器序号,垂直直线划分出4段波形窗,分别对应P波、P波尾波、S波和S波尾波,4段波形的长度相同,等于S波与P波到时差的一半。
|
图 5 P波、P波尾波、S波和S波尾波选取 (a)地震;(b)爆破 Fig.5 P, P coda, S and S coda |
波形提取完成后,计算事件各频带上不同波形段的平均能量值,计算公式为
| $ P = \frac{1}{N}\sum\limits_{i = 1}^N {y_i^2} $ | (1) |
其中,N为波形中采样点个数,yi为波形中第i个采样点的振幅值。最终,每个事件得到一组4×8的参数矩阵,即为该事件的能量特征。表 2、表 3分别给出地震与爆破事件的能量特征值。
| 表 2 2015年7月29日ML 1.3地震事件能量特征 Table 2 Energy characteristics for the ML 1.3 earthquake on July 29, 2015 |
| 表 3 2015年9月26日ML 2.0爆破事件能量特征 Table 3 Energy characteristics for the ML 2.0 explosion on September 26, 2015 |
文中识别算法使用RBF神经网络。RBF神经网络是一种经典的前馈型3层人工神经网络,由输入层、隐含层和输出层组成,其中隐含层转换函数通常使用局部响应的高斯函数。与其他前馈型神经网络相比,尽管RBF神经网络实现同样功能需要更多神经元,但其训练神经网络所花费的时间更少,还可以以任意精度逼近任意连续函数,其隐层中的神经元越多,逼近越精确(Haykin,2001)。
文中示例事件识别属二元分类识别,因此使用结构较为简单的单输出神经网络结构。本研究所用RBF神经网络结构见图 6。

|
图 6 RBF神经网络结构 Fig.6 Structure of RBF neural networks |
文中神经网络各层参数如下:①输入层:神经网络的输入为上一节中提取的32个能量特征值,因此输入层节点数为32,节点权值均为1;②隐含层:径向基函数gi(x)选择应用广泛的高斯函数,函数表达式为
| $ {g_i}(x) = exp\left[ { - \frac{{\parallel x - {C_i}{\parallel ^2}}}{{{\sigma ^2}}}} \right] $ | (2) |
式中Ci为第i个基函数中心向量,方差
| $ {y_n} = \sum\limits_1^m {{W_{ni}}{g_i}(x)} i = 1, 2, 3, \ldots m $ | (3) |
式中,n为样本输入数据数量,m为隐含层节点数,gi(x)为神经网络的径向基函数。由于文中示例属较为简单的二元分类识别,因此神经网络的输出以0作为识别阈值,输出结果大于0的判定为地震事件,小于0的判定为爆破事件,等于0的则作为无法判定类型事件。
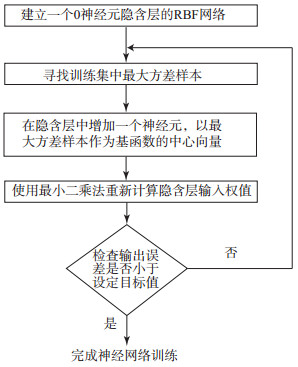
为减少对神经网络训练的计算量,提高算法时效性,在训练集中直接选取基函数中心进行隐含层训练。训练集中2类事件的输出分别是:地震事件的输出设定为1,爆破事件的输出设定为-1。文中示例的神经网络训练流程见图 7。
|
图 7 神经网络训练流程 Fig.7 Flowchart of neural network training procedure |
RBF神经网络的训练和测试分别由训练数据集和测试数据集完成。文中训练数据集由地震和爆破事件记录中各50条清晰波形组成;测试数据集由剩余的126条地震波形和113条爆破波形组成。运用式(1),计算各数据集中不同事件的能量特征值,并使用训练数据集对神经网络进行训练,训练完成后,使用神经网络分别对训练数据集和测试数据集进行分类识别,识别结果见表 4。由表 4可见,126个地震事件中有11个误识别为爆破事件,而113个爆破事件中有17个误识别为地震事件,未出现无法判定事件,总体识别准确率为88.1%。
| 表 4 RBF神经网络分类识别结果 Table 4 Discrimination results based on RBF neural network |
利用地震与爆破事件的P波和S波在不同频带上能量的分布差异,结合RBF神经网络技术,对地震与爆破事件波形进行自动分类,并将该方法用于2015—2017年桂林及周边地区68个地震事件和74个爆破事件的分类识别,结果表明,文中提出的识别方法对地震事件识别的准确率为91.2%,对爆破事件识别的准确率为85%,总体识别率为88.1%,说明该方法对地震与爆破事件的分类识别具有一定效果。将该方法应用于具有庞大数据量的小震级地震事件和爆破事件分类中,可以有效减少事件分类识别的工作量。如果配合人工分析,结合发震时刻、初动方向、P波与S波振幅比等特征,可进一步减少事件类别误报。
4.2 讨论近年来,许多地震与爆破事件自动分类识别技术具有较高识别率,如:毕明霞等(2011)对事件波形进行希尔伯特—黄变换(Hilbert-Huang Transform,HHT),将原始信号中提取的模态分量最大幅值对应周期和倒谱平均值作为特征,运用支持向量机进行分类识别,识别率介于75%—94%;Yılmaz等(2013)对2002—2010年土耳其黑海东岸的地震事件和爆破事件,依据S波与P波振幅比、波形复杂性和时频谱特征进行分类识别,未给出总体误差估计,但单站成功率在73%—100%;Kuyuk等(2014)以时间相关参数、复杂度和S—P峰值幅值比作为特征指标,使用线性和非线性判别方法,对伊斯坦布尔附近的地震与爆破事件进行分类识别,识别率达95.5%—97.6%;范晓易等(2019)对山东地区2006—2017年记录的地震、爆破和塌陷事件,利用香农熵特征,结合LIBSVM支持向量机技术进行识别,总体识别率在80%—95%。对比发现,文中提出的研究方法与近年来同类研究水平相近。
研究发现,若训练数据集中有错误类型事件,则错误事件特征将被神经网络学习,导致分类识别的准确率下降。因此,在神经网络开始训练前,对训练数据集中的100个事件重新进行人工分析判别,从而确保训练数据集的正确性。
不同地区在地质环境、构造背景、地层岩性等存在差异,且各地区测震台网使用的地震计参数型号也不尽相同,导致波形记录特征存在的差别较大。文中提及的事件类型识别方法用于其他地区事件时,需要结合当地事件特征,重新对神经网络进行训练。今后,我们将收集更多样本事件,引入更具有广泛性的事件特征,不断提升识别方法的准确性。
毕明霞, 黄汉明, 边银菊, 李锐, 陈银燕, 赵静. 2011. 天然地震与人工爆破波形信号HHT特征提取和SVM识别研究[J]. 地球物理学进展, 26(4): 1157-1164. DOI:10.3969/j.issn.1004-2903.2011.04.004 |
边银菊, 王婷婷, 郭永霞. 2012. 用决策方法识别地震与爆破[J]. 地震学报, 34(3): 397-407. DOI:10.3969/j.issn.0253-3782.2012.03.012 |
范晓易, 曲均浩, 曲保安, 刘方斌, 山长仑, 周少辉. 2019. 支持向量分类机LIBSVM方法识别天然地震、爆破与塌陷[J]. 大地测量与地球动力学, 39(9): 916-918. |
黄汉明, 边银菊, 卢世军, 蒋正锋, 李锐. 2010. 天然地震与人工爆破的波形小波特征研究[J]. 地震学报, 32(3): 270-276. DOI:10.3969/j.issn.0253-3782.2010.03.002 |
靳玉贞, 林木金, 范晓瑜, 刘晓萍, 何佳, 杨世英, 孟彩菊. 2015. 山西地区爆破、塌陷(矿震)特殊地震动特征识别[J]. 地震地磁观测与研究, 36(3): 63-66. DOI:10.3969/j.issn.1003-3246.2015.03.012 |
王婷婷, 边银菊, 张博. 2014. 地震与爆破的小波包识别判据研究[J]. 地震学报, 36(2): 220-232. DOI:10.3969/j.issn.0253-3782.2014.02.007 |
王婷婷, 边银菊. 2015. 振幅衰减特性在地震与爆破识别中的应用[J]. 地震学报, 37(1): 169-179. |
杨芳, 朱嘉健, 刘智, 吴彬. 2016. 广东地区地震与爆破事件识别方法研究[J]. 华南地震, 36(3): 110-115. |
张博, 边银菊, 王婷婷. 2014. 用逐步代价最小决策法识别地震与爆破[J]. 地震学报, 36(2): 233-243. DOI:10.3969/j.issn.0253-3782.2014.02.008 |
张萍, 蒋秀琴, 苗春兰, 邹向荣. 2005. 爆破、矿震与地震的波谱差异[J]. 地震地磁观测与研究, 26(3): 24-34. DOI:10.3969/j.issn.1003-3246.2005.03.004 |
中国地震局监测预报司. 2017. 测震学原理与方法[M]. 北京: 地震出版社, 283-284.
|
Beccar-Varela M P, Gonzalez-Huizar H, Mariani M C, Tweneboah O K. 2016. Use of wavelets techniques to discriminate between explosions and natural earthquakes[J]. Physica A:Statistical Mechanics and its Applications, 457: 42-51. DOI:10.1016/j.physa.2016.03.077 |
Fäh D, Koch K. 2002. Discrimination between earthquakes and chemical explosions by multivariate statistical analysis:a case study for Switzerland[J]. Bulletin of the Seismological Society of America, 92(5): 1795-1805. DOI:10.1785/0120010166 |
Haykin S. 2001. Neural networks:a comprehensive foundation[J]. Beijing:Tsinghua University Press: 278. |
Kuyuk H S, Yildirim E, Dogan E, Horasan G. 2012. Application of k-means and Gaussian mixture model for classification of seismic activities in Istanbul[J]. Nonlinear Process Geophys, 19(4): 411-419. DOI:10.5194/npg-19-411-2012 |
Kuyuk H S, Yildirim E, Dogan E, Horasan G. 2014. Clustering seismic activities using linear and nonlinear discriminant analysis[J]. Journal of Earth Science, 25(1): 140-145. DOI:10.1007/s12583-014-0406-x |
Lyubushin A A, Kaláb A, Lednická Z M, Haggag H M. 2013. Discrimination of earthquakes and explosions using multi-fractal singularity spectrums properties[J]. Journal of Seismology, 17(1): 975-983. |
Pasyanos M E. 2010. A general method to estimate earthquake moment and magnitude using regional phase amplitudes[J]. Bulletin of the Seismological Society of America, 100(4): 1724-1732. DOI:10.1785/0120090363 |
Yılmaz Ş, Bayrak Y, Cinar H. 2013. Discrimination of earthquakes and quarry blasts in the eastern Black Sea region of Turkey[J]. Journal of Seismology, 17(2): 721-734. DOI:10.1007/s10950-012-9348-x |
 2020, Vol. 41
2020, Vol. 41

